机床主轴机构模态和振动特性分析与主轴径向回转误测试方法的研究

Study on Analysis of Modal and Vibration Characteristics and Test Method of Radial Rotation Error of Machine Tool Spindle

摘要: 本文以一特定机床主轴作为研究对象，首先利用传递矩阵法对主轴的参数进行确定、简化轴承等模型，使用有限元法对主轴模型进行带预应力的模态仿真。随后，本文使用垂直两点法测试了多组不同转速下的主轴回转误，并使用频域两点法对误差进行分离计算得到同步误差和异步误差。结果显示，由异步误差异常高导致的回转误差异常高转速区间的转速基频与模态分析结果的第一、四、五阶模态频率相对应。为提高机床主轴的精度和稳定性提供理论依据和实验基础。

Abstract: In this article, a specific machine tool spindle is used as the research object. First, the transfer ma-trix method is used to determine the parameters of the spindle, simplify the bearing and other models, and the finite element method is used to perform modal simulation of the spindle model with prestress. Subsequently, this paper used the vertical two-point method to test the rotation er-rors of multiple sets of spindles at different speeds, and used the frequency domain two-point method to separate the errors and calculate the synchronization error and asynchronous error. The results show that the fundamental frequency of the rotation speed interval of the abnormally high rotation error caused by the abnormally high asynchronous error corresponds to the first, fourth, and fifth-order modal frequencies of the modal analysis results. It provides a theoretical basis and an experimental basis for improving the accuracy and stability of the machine tool spindle.

1. 引言

随着数控机床的广泛应用，机床主轴的精度和稳定性对加工质量和效率的影响越来越大。其中，主轴径向回转误差是影响主轴精度和稳定性的重要因素之一 [1] 。对回转误差的测试和振动模态的研究可用于机床加工的预测和补偿，提高零件的加工精度和表面质量，对于提高机床主轴的精度和稳定性具有重要意义 [2] 。

目前，国内外学者已经对机床主轴的模态仿真计算方法和回转误差测试方法进行了广泛的研究。在主轴模态计算仿真方面，朱冬等人 [3] 通过模态分析得到了电主轴的固有频率、振型和临界转速对数控铣床电主轴故障诊断为高速电主轴结构设计和轴承最佳预紧力的确定提供了分析依据。徐壮 [4] 详尽的给出了联轴器传动型直结式铣削主轴的结构分析，并为装配与调试提供了改进方法。刘成颖等人 [5] 基于Hertz理论和最小二乘法理论建立了高速电主轴中主轴–机壳振动传递力学模型，利用Ansys软件求解出电主轴固定基座的刚度，并进行实验验证与仿真分析。黄康等人 [6] 采用多体传递矩阵法对电主轴的某些参数进行简化与确定，在此基础上采用有限元仿真方法建立电主轴仿真模型，并使用仿真软件Hypermesh进行Optistruct器件的振动仿真，以确定系统的振动特性。王玉伟等人 [7] 分别建立主轴转子及主轴部件的有限元模型，对有限元模型中添加的弹簧及电机约束边界条件进行了研究，并分别对以上两个有限元模型进行模态计算。李树森等人 [8] 设计了一种精密气悬浮主轴并在ANSYS Workbench中建立主轴转子的有限元模型，对设计转速进行模态分析和验证。

对于主轴回转误差测试，国际标准ISO 230-7 [9] 制定了机床旋转轴的几何精度测试标准。陆峰等人 [10] 建立误差分离数学模型，对垂直两点法测量电主轴回转精度进行分析，利用垂直两点法分离误差方法对实验数据进行处理，得到电主轴在不同转速下的回转精度，找出影响电主轴回转精度的因素并进行了归纳。美国雄狮精密公司(Lion Precision) [11] 研发了主轴回转误差测量仪，使回转误差的测试可以做到实时检测与快速分析。日本的青木保雄等人 [12] 提出了3点法圆度测定法，使用三个位移传感器动态监测回转轴的圆度，分离回转误差。韩玉稳等人 [13] 对机床主轴精度进行了检测，并用最小二乘法拟合测试结果和机床传感器数据，给出了精度补偿的数学模型。迟玉伦等人 [14] 提出了基于多步误差分离法的主轴回转误差检测方法，在不借助标准球或者标准棒的情况下对数控铣床的主轴外轮廓进行直接测量，并通过数据降噪处理后分离得到主轴回转误差。

但是，以上研究局限于对振动模态的分析和对回转误差分离方法的研究，而影响主轴加工性能的因素是多方面的，单一的研究对象无法与主轴系统性的联系起来。本文将从机床主轴的结构和振动特性入手，探讨机床主轴机构模态和振动特性对主轴径向回转误差的影响。为提高机床主轴的精度和稳定性提供理论依据和实验基础。

2. 直结式机械主轴回转误差分离方法和数学模型的建立

2.1. 直结式主轴结构特性及组成

本文研究对象为沈阳机床i5m1立式数控钻铣床的直结式主轴，其结构示意图如图1所示。主轴结构包括芯轴、拉杆、外套、轴承、套圈、隔圈、拉爪、隔环以及各种销、垫圈、碟簧等。该主轴使用BT30标准刀具，采用气动拉刀装置。在结构上，该主轴的回转轴芯轴由联轴器与主轴电机等驱动机构直接连接。

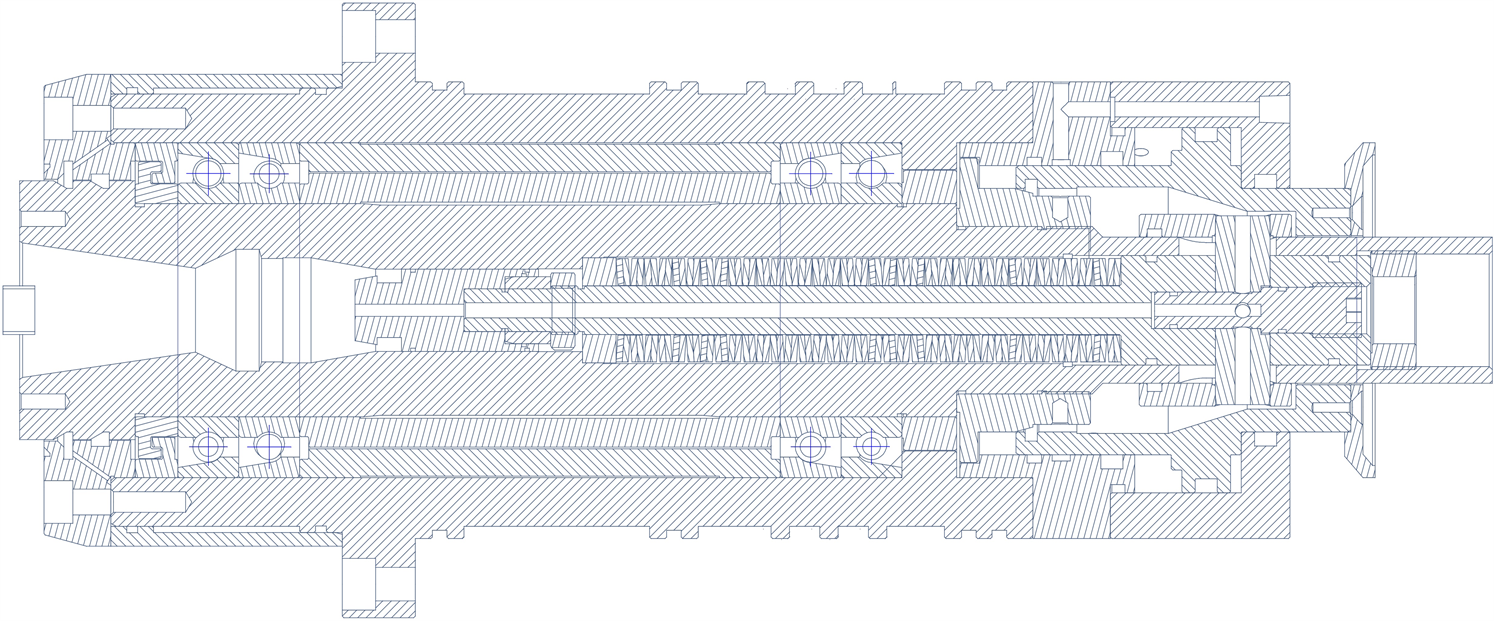
Figure 1. Schematic diagram of spindle structure

图1. 主轴结构示意图

从结构上看，该直结式主轴主要特点有：

1) 可实现主轴转速的高速化，有效改善主轴高速综合性能；

2) 机械结构简单，转动惯量小，能实现高速度和高的角加速度，有利于快速准停；

3) 减少齿轮传动或皮带传动等的中间传动环节，避免传动链导入的振动和噪声，提高了主轴回转精度。

2.2. 基于传递矩阵法的主轴动态特性分析

针对本文这种结构方案的主轴系统，使用传递矩阵法来进行分析建模，设置参数进行振动特性分析来反映电主轴系统的动态特性。

传递矩阵法即将系统化分为若干单元，在相邻两个小单元的分界面上，用位移协调和力的平衡条件来相互联系，且每个小单元可运用到牛顿第二定律建立运动方程 [6] 。根据运动方程及边界条件得到单元另一侧的力和位移。依此进行下去最后可求得问题的解。通常把分界面上的力和位移变量的列向量记作状态向量。解题从边界开始逐步另一方向，且相邻单元的状态向量用矩阵联系，将这一方法一般称为传递矩阵法。

依据传递矩阵法的相关建模原理，针对所研究的电主轴振动系统建立的动力学集总参数模型如图2，在实际计算中，为简化问题，可将圆盘及右边的轴段组合为一构件，如图3(a)所示，该构件的传递矩阵推导如下。

具有弹性支承的圆盘，受力分析见图3(b)。

Figure 2. Simplified model of spindle transfer matrix method

图2. 主轴传递矩阵法简化模型

Figure 3. Force analysis

图3. 受力分析

当转子进动角速度 $\Omega =\omega$ (转子自转角速度)时，系统作同步正向进动，得到圆盘的惯性力为 $m_i{Y}_i{\omega }^2$ ，惯性力矩为： $\left(J_{di}-J_{pi}\right){\omega }^2{\theta }_i$

由达朗伯原理得到：

$\{\begin{array}{l}{Q}_i^R=Q_i^L+m_i{\omega }^2-k_{ri}{Y}_i\hfill \\ M_i^R=M_i^L-\left(J_{di}-J_{pi}\right){\omega }^2{\theta }_i+k_{\theta i}{\theta }_i\hfill \end{array}$ (1)

且有：

$\{\begin{array}{l}{Q}_i^R=Q_i^L=Q_i\hfill \\ Y_i^R=Y_i^L=Y_i\hfill \end{array}$ (2)

综合以上得到具有弹性支承的圆盘的传递矩阵为：

$D_i=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& \left(J_{pi}-J_{di}\right){\omega }^2+k_{\theta i}& 1& 0\\ m_i{\omega }^2-k_{ri}& 0& 0& 1\end{array}\right]$ (3)

$J_d$ ——转子直径转动惯量； $J_p$ ——转子极转动惯量； $m_i$ ——节点处总质量(轴段与圆盘质量之和)。

同理可以推导无弹性圆盘的传递矩阵 $C_i$ 。

$C_i=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& \left(J_{pi}-J_{di}\right){\omega }^2& 1& 0\\ m_i{\omega }^2& 0& 0& 1\end{array}\right]$ (4)

故由以上的传递矩阵得到组合构件如图3(a)所示的传递矩阵 $U^{\prime }$ 。

$\begin{array}{c}{U}^{\prime }=B_i{D}_i=\left[\begin{array}{cccc}1& l_i& \frac{l_i^2}{2E{I}_i}& \frac{l_i^3}{6E{I}_i}\left(1-\gamma \right)\\ 0& 1& \frac{l_i}{2E{I}_i}& \frac{l_i^2}{2E{I}_i}\\ 0& 0& 1& l_i\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& \left(J_{pi}-J_{di}\right){\omega }^2+k_{\theta i}& 1& 0\\ m_i{\omega }^2-k_{ri}& 0& 0& 1\end{array}\right]\\ =\left[\begin{array}{cccc}1+\frac{l_i^3}{6E{I}_i}(1-\gamma )\left(m_i{\omega }^2-k_{ri}\right)& l_i+\frac{l_i^2}{2E{I}_i}\left[\left(J_p-J_d\right){\omega }^2+k_{\theta i}\right]& \frac{l_i^2}{2E{I}_i}& \frac{l_i^3}{6E{I}_i}\left(1-\gamma \right)\\ \frac{l_i^2}{2E{I}_i}\left(m_i{\omega }^2-k_{ri}\right)& 1+\frac{l_i}{E{I}_i}\left[\left(J_p-J_d\right){\omega }^2+k_{\theta i}\right]& \frac{l_i}{E{I}_i}& \frac{l_i^2}{2E{I}_i}\\ l_i\left(m_i{\omega }^2-k_{ri}\right)& \left(J_p-J_d\right){\omega }^2+k_{\theta i}& 1& l_i\\ \left(m_i{\omega }^2-k_{ri}\right)& 0& 0& 1\end{array}\right]\end{array}$ (5)

以上得到的传递矩阵 $B_i,C_i,D_i,U^{\prime }$ 作为相应的 $U_i$ ，于是，电主轴系统总的传递矩阵：

$U=U_n{U}_{n-1}\cdots U_3{U}_2{U}_1$ (6)

其中，总的传递方程：

$Z_n=U{Z}_1$ (7)

代入初始边界条件求解，得到总的传递方程，并对应求解出相应的状态向量，即获取系统振动的振型与固有频率。

2.3. 主轴回转误差分离的垂直两点法

主轴回转误差是主轴实际回转轴线对其理想回转轴线的位置偏差。可以分解为三种情况：径向误差、轴向误差、倾角摆动三种基本形式。主轴回转径向误差运动是指在回转过程中回转轴线偏离理想轴线位置而出现的附加运动，是评价机床动态性能的一项重要指标，是影响机床工作精度的主要因素。

两点测量法是根据日本学者青木保雄和大园成夫在1966年提出的三点测量法的基础上，将三个传感器中的两个传感器合并，演化成两点测量法 [12] 。三点测量法的测量原理是使用三个同样的传感器按照一定角度垂直布置被测标准球的同一截面上对主轴误差进行测量，并利用频谱技术把圆度误差与回转误差分离。

根据ISO 230-7所定义的主轴回转误差测试标准，使用两点法分离主轴回转误差。其原理如图4所示。对处理后的原始信号做傅里叶变换，将转速基频及其倍频部分分离为同步误差，其余部分为异步误差，同步误差还可以进一步分离，其的第一项为偏心误差，其余项为圆度误差。

根据三点法误差分离基本方程

$\{\begin{array}{l}{S}_0=r\left(\theta \right)+x\left(\theta \right)\\ S_1=r\left(\theta -\alpha \right)+x\left(\theta \right)\cos \alpha +y\left(\theta \right)\sin \alpha \\ S_2=r\left(\theta -\beta \right)+x\left(\theta \right)\cos \beta +y\left(\theta \right)\sin \beta \end{array}$ (8)

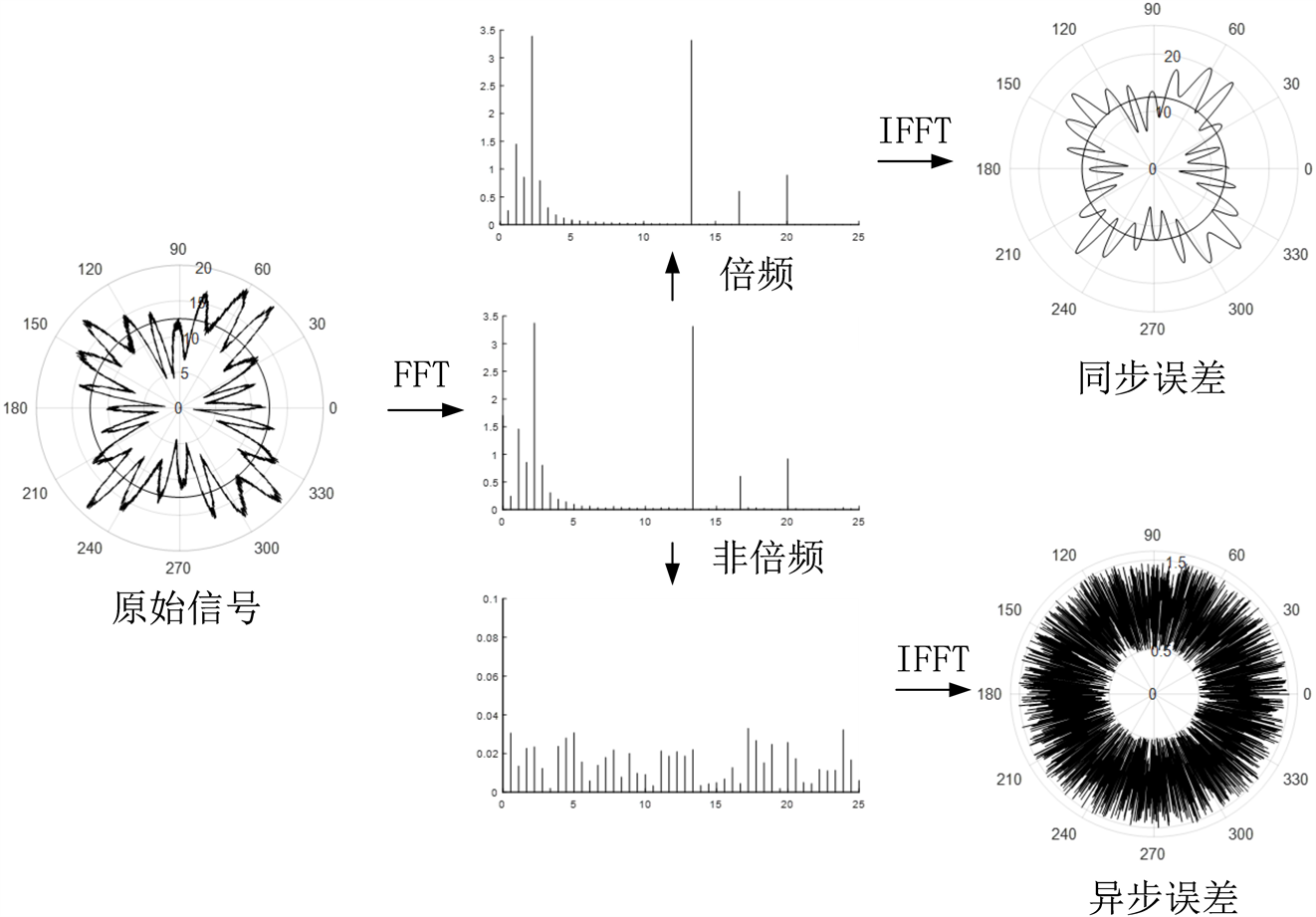
Figure 4. Schematic diagram of spindle rotation error separation

图4. 主轴回转误差分离示意图

引入传感器的标定系数 $c_0、c_1、c_2$ ，则以上三式分别乘标定系数得到：

$C\left(\theta \right)=c_0{S}_0\left(\theta \right)+c_1{S}_1\left(\theta \right)+c_2{S}_2\left(\theta \right)$ (9)

根据(8)式展开，若要分离出圆度误差 $r\left(\theta \right)$ ，则需要 $x\left(\theta \right)$ 、 $y\left(\theta \right)$ 前的系数为0，则得到：

$\{\begin{array}{l}{c}_0+c_1\cos \alpha +c_2\cos \beta =0\\ c_1\sin \alpha +c_2\sin \beta =0\end{array}$ (10)

此线性方程组有无穷多解，取 $c_0=1$ ，得到一组特解为：

$\{\begin{array}{c}{c}_0=0\\ c_1=\frac{\sin \beta }{\sin \left(\alpha -\beta \right)}\\ c_2=-\frac{\sin \alpha }{\sin \left(\alpha -\beta \right)}\end{array}$ (11)

在三点法中，若取 $\alpha =\frac{\pi }{2}$ 、 $\beta =\pi -\Delta \theta$ (采样间隔 $\Delta \theta =\frac{2\pi }{N}$ )当N较大时，(11)式中的 $c_1$ 、 $c_2$ 可以写成：

$\{\begin{array}{l}{c}_1=\frac{\sin \beta }{\sin \left(\alpha -\beta \right)}=\frac{\sin \left(\pi -\Delta \theta \right)}{\sin \left(\frac{\pi }{2}-\pi +\Delta \theta \right)}=\frac{\sin \left(\Delta \theta \right)}{\cos \left(\Delta \theta \right)}\approx 0\\ c_2=-\frac{\sin \alpha }{\sin \left(\alpha -\beta \right)}=-\frac{\sin \left(\frac{\pi }{2}\right)}{\sin \left(\frac{\pi }{2}-\pi +\Delta \theta \right)}\approx 1\end{array}$

当 $c_1=0$ 时，传感器 $S_1$ 的输出信号在加权中占有很小的比重，可以忽略不记。那么，那么三点法就演化成了垂直两点法。(9)式就可以写成：

$C\left(\theta \right)\approx c_{0}r\left(\theta \right)+c_{2}r\left(\theta +\pi -\Delta \theta \right)$ (12)

将(12)式离散化得到：

$C\left(i\right)\approx c_{0}r\left(i\right)+c_{2}r\left(i+\frac{N}{2}-1\right)$ (13)

对(13)式进行离散傅里叶变换(FFT)，得到：

$R_f\left(n\right)W\left(n\right)\approx C_f\left(n\right)$ (14)

$R_f\left(n\right)$ 为时域上电主轴的圆度误差 $r\left(i\right)$ ， $C_f\left(n\right)$ 为时域上圆度误差和回转误差的混合定好； $W\left(n\right)$ 为权函数，如下：

$\begin{array}{l}W\left(n\right)\approx 1+c_2{\text{e}}^{\frac{j2\pi n{p}_2}{N}}\\ p_2=\frac{\beta N}{2\pi }=\frac{N}{2}-1\end{array}$ (15)

当 $W\left(n\right)\ne 0$ 时，有：

$R_f\left(n\right)\approx C_f\left(n\right)/W\left(n\right)$ (16)

对(16)式进行离散傅里叶逆变换(IFFT)，得到：

$r_i\left(n\right)\approx F^{-1}\left[R_f\left(n\right)\right]$ (17)

将(17)式带入(8)式可以得到：

$\{\begin{array}{c}x\left(\theta \right)=S_0\left(i\right)-r\left(i\right)\\ y\left(\theta \right)=S_2\left(i\right)-r\left(i+p_2\right)\end{array}$ (18)

由此得到分离后的同步误差和异步误差。同步误差可以进一步分离为圆度误差和偏心误差。

3. 电主轴模态分析

根据传递矩阵法，选取目标主轴的芯轴进行分析，使用ANSYS软件，建立有预应力的模态分析。根据芯轴实际受力情况进行加载和约束，划分网格后计算求解。

分析得到的频率和振型图结果如下，表1为前18阶模态的频率计算结果，取前6阶绘制模态振型图如下。

Table 1. Modal analysis simulation results

表1. 模态分析仿真结果

前6阶模态结果绘图如图5所示。

(a) 一阶振型 (b) 二阶振型 (c) 三阶振型 (d) 四阶振型 (e) 五阶振型 (f) 六阶振型

Figure 5. Simulation result mode diagram

图5. 仿真结果振型图

Figure 6. Spindle rotation error test platform

图6. 主轴回转误差测试平台

可以看到，对于主轴轴端的径向回转误差影响较大的几个模态分别是一阶、四阶、五阶和六阶。

4. 主轴回转误差测试

使用美国雄狮精密SEA主轴回转误差分析仪对该主轴进行测试。测试平台如图6(a)所示，其中的图6(b)为用来安装传感器的传感器巢和电容式传感器以及安装在主轴上的标准球，电容式传感器插入传感器巢的孔中并由六角螺丝固定，标准球被固定在一定心刀具座(BT40)中，由主轴上的打刀缸和拉爪固定在主轴上。图(c)为传感器驱动模块和数据采集卡，驱动模块包括电源和校零标尺，采集卡使用NI-6306采集卡，通过USB连接计算机。图(d)为数据采集和分析软件界面，用来设置采样率、平均圈数等参数，并保存测试结果和原始数据。

将电容式传感器安装在传感器巢中并校零，设置每20圈进行一次平均，间隔100 rpm测试主轴从100 rpm到8000 rpm转速区间的回转误差，计算分离后的同步误差和异步误差值，得到在不同转速下的回转误差结果，部分数据结果如表2所示。

Table 2. Rotation error analysis results

表2. 回转误差分析结果

将所有数据汇总，绘制折线图如图7所示。

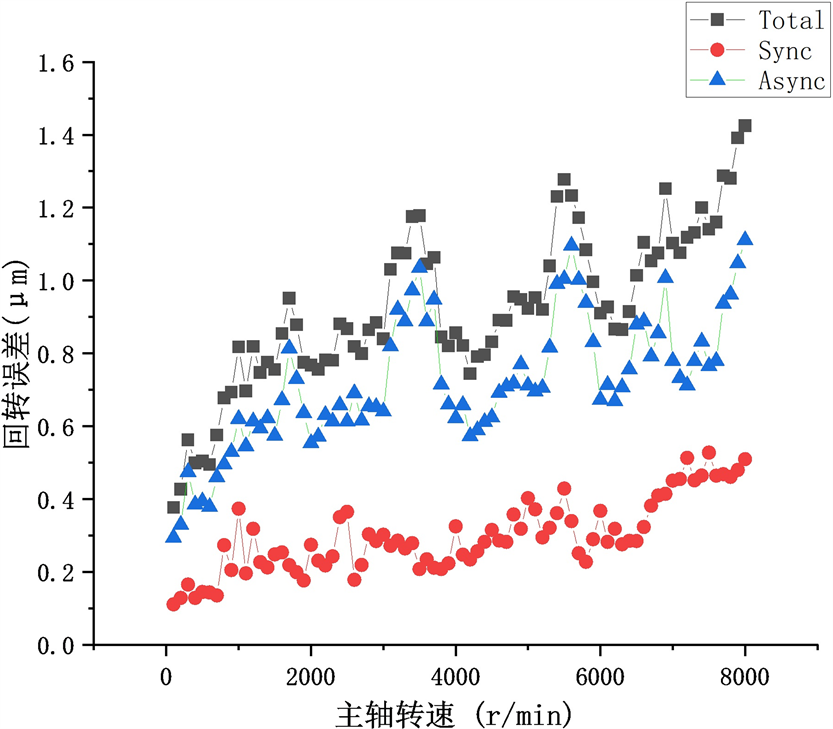
Figure 7. Line chart of error separation result

图7. 误差分离结果折线图

总的来看，主轴回转误差随转速的提高不断提高，但增加并不是线性的，在3500~4000 rpm、5400~5900 rpm、7200~8000这几个转速区间出现了异步误差异常高的情况，导致了整体回转误差偏高。而同步误差随转速的增加不断增加，较为线性。

5. 结论

传递矩阵法主要解决一维结构系统静力学和动力学问题，其建立模型灵活，计算效率高为该方法的优点，对于本文复杂的主轴系统，在采用有限元法的同时，利用传递矩阵法对主轴的参数进行确定、简化轴承等模型，上述工作在有限元分析时起到突出的作用。

用垂直两点法进行测量，降低了测量装置的安装难度，装配容易，能很容易地测得主轴的混合误差，并能够分离出同步误差和异步误差，直观地显示回转误差的轨迹图，做出进一步分析。

已知主轴电机的极对数P = 6，则三个转速异常高区间的转速基频与模态中的第一、四、五阶模态频率相对应。则可以确定主轴在该转速区间回转精度较差是由于主轴振动导致的。在编制加工工艺参数过程中，应尽量避开该转速区间，使主轴运行更加平稳，进而保证加工质量稳定。