1. 引言
自碳达峰、碳中和的低碳发展目标明确提出以来,建设以新能源为主导的现代电力系统已成为中国电力行业发展改革的新导向。国家大力推动清洁能源发展,但以光伏、风能为主的微电网出力具有间歇性和波动性,接入电力系统会损坏系统的稳定性。在微电网中接入储能系统能量可以在时间维度上实现转移,平抑功率波动,提高电能质量 [1] 。采用合理的优化配置方案能够有效减少经济成本和提高系统稳定性。因此,对微电网的优化配置进行研究具有极其重要的意义。
针对微电网的优化配置问题,国内外已有相关研究。文献 [2] 采用多种策略对麻雀搜索算法进行改进,并进行微电网的容量优化配置,验证所提策略在容量优化问题中具有更好的性能。文献 [3] 采用改进的海洋捕食者算法进行配电网储能的配置,验证其在储能优化配置问题上的有效性,但该算法仅提高了收敛精度,收敛速度能力有待考察。文献 [4] 建立考虑经济性和环保性的综合成本最低为目标函数的独立微电网容量优化运行模型,并利用改进的粒子群优化算法对模型进行求解,但其收敛精度有待进一步提升。文献 [5] 以运行收益最大为目标,采用基于改进蚁群的动态规划算法进行光储微电网的容量优化配置,验证算法的适用性和优越性,但其考虑因素较少,未能提供更加精准的参考。
在上述研究基础上,本文以风–光–燃–柴–储型微电网为研究对象,对微电网负荷端的价格型需求响应进行建模,以投资运维成本和运行成本最小为目标建立双层优化配置模型,采用基于多种策略改进的海鸥优化算法,并与Cplex求解器联合运算求解,进行微电网的优化配置,通过仿真实验验证所提策略的有效性以及能够降低微电网的各项成本。
2. 需求响应模型
价格型需求响应(Price Demand Response, PDR)基于价格的计划为以电价的形式引导用户改变用电习惯。价格型需求响应一般采用弹性系数表示电价变化量对用户参加需求响应量的影响 [6] ,表达式为
(1)
式中,e为电量电价的弹性系数,
为电量q的相对变化量,
为电价c的相对变化量。
对于t时段的用户对电价的响应率的表达式为
(2)
式中,
为电量单价的弹性矩阵,
为自适应弹性系数,
为交叉弹性系数。
3. 微电网双层优化配置模型
3.1. 双层优化配置模型框架
如图1所示,双层规划可兼顾上下层双方的利益。在上层优化配置模型中,根据微电网的运行情况相关参数对储能系统进行配置,优化目标为日运行和维护成本最低。下层用于求解微电网系统的运行问题,结果受外层模型决策变量影响,目标函数为运行成本及环保惩罚成本最低。
3.2. 上层容量优化模型
1、目标函数
以日均投资成本和运行成本最小为目标建立目标函数。计算公式为
(3)
式中,
为投资成本,
为下层运行成本。其中
(4)
式中,
为折现率,
为寿命规划周期,
为单位容量投资成本;t为一天的24小时,
。
2、约束条件
(5)
式中:
为电池容量,
为电池安装容量上限。
3.3. 下层优化运行模型
1、目标函数
储能系统优化运行和需求响应协同作用下可以最大程度的减小负荷量,降低成本,增加收益。下层模型以日调度周期内成本最低为目标,包括需求响应和储能优化运行带来的费用减少、能量废弃成本以及环境污染治理成本的减少。综合得下层目标函数为:
(6)
为运维成本,
为燃料成本,
为购电成本,
为环境污染治理成本。
1) 运维成本
(7)
式中,
为各单元的运维成本系数,
为第s个设备在t时段的功率。
2) 燃料成本
(8)
式中,
为第s个设备的燃料成本,
为s个设备t时刻的功率。
3) 购电成本
(9)
式中,
为购电单价,
为购电功率。
4) 环境污染治理成本
(10)
式中,M为污染物的种类,
第k种污染物的排放系数,
为第k种污染物的环境价值,
为污染物的污染罚款,
为第s个设备的功率。
2、约束条件
1) 燃气轮机约束
(11)
、
分别为燃气轮机出力的上下限,受其最小负载功率和额定功率的约束。
2) 柴油发电机约束
(12)
、
分别为柴油发电机出力的上下限。
3) 电池储能荷电状态约束
(13)
(14)
(15)
式中,
为电池在t时刻的荷电状态;
为电池的充放电效率;
和
分别为电池充电功率和放电功率。
4) 充放电功率约束
(16)
(17)
式中,
和
分别代表电池放电和充电的最大功率;
和
表示电池的运行状况,
为1代表电池处于放电状态,
为1代表电池处于充电状态,两者不能同时为1。
5) 购电功率约束
(18)
和
分别为购电的最小功率和最大功率。
6) 需求响应约束
响应前后总负荷量不变
(19)
式中,
为微电网的负荷需求。
7) 功率平衡约束
(20)
4. 改进海鸥优化算法
海鸥优化算法(SOA)是于2019年由Gaurav Dhiman提出的新型生物启发式算法 [7] ,该算法由于对大规模约束优化问题求解的适应性较强而比其他算法更具有竞争力。相较于其他算法,海鸥算法面对复杂问题存在收敛速度较慢、易收敛于局部最优解的问题,需对算法进行改进,以提高其收敛速度和精度。
1、混沌反向学习策略
(21)
其中,i为种群数量,j为混沌变量序号,μ为混沌系数,取值范围为(0, 2],μ越大,混沌性越好,一般选取μ = 2。通过公式可以得到n个混沌序列,将序列作逆映射到搜索空间中获取个体位置向量X,群
,
,改进后的种群初始化公式可表示为:
(22)
由种群X计算反向种群
,反向种群个体
表示为
。
(23)
通过对种群X和反向种群进行OX合并,得到新种群
,计算新种群的目标函数值并排序,选取其中适应度值最好的N个个体作为初始种群。
2、随机混合变异
为加快算法的收敛速度、增强全局搜索能力、降低算法陷入局部最优的可能性,提出针对最优个体的自适应混合变异策略。
1) 随机差分变异
差分进化是利用当前种群的距离和方向信息指引搜索的一种进化算法。该算法在变异阶段 [8] ,通过随机选择三个向量来生成变异个体
(24)
式中,F∈[0,2]为缩放因子。随机差分变异利用当前个体、当前最优个体和在种群中随机选择个体进行随机差分得到新个体。
(25)
其中,
、
均为(0, 1)的随机数,t为当前迭代次数,
为当前最优个体,
为随机选取的个体。
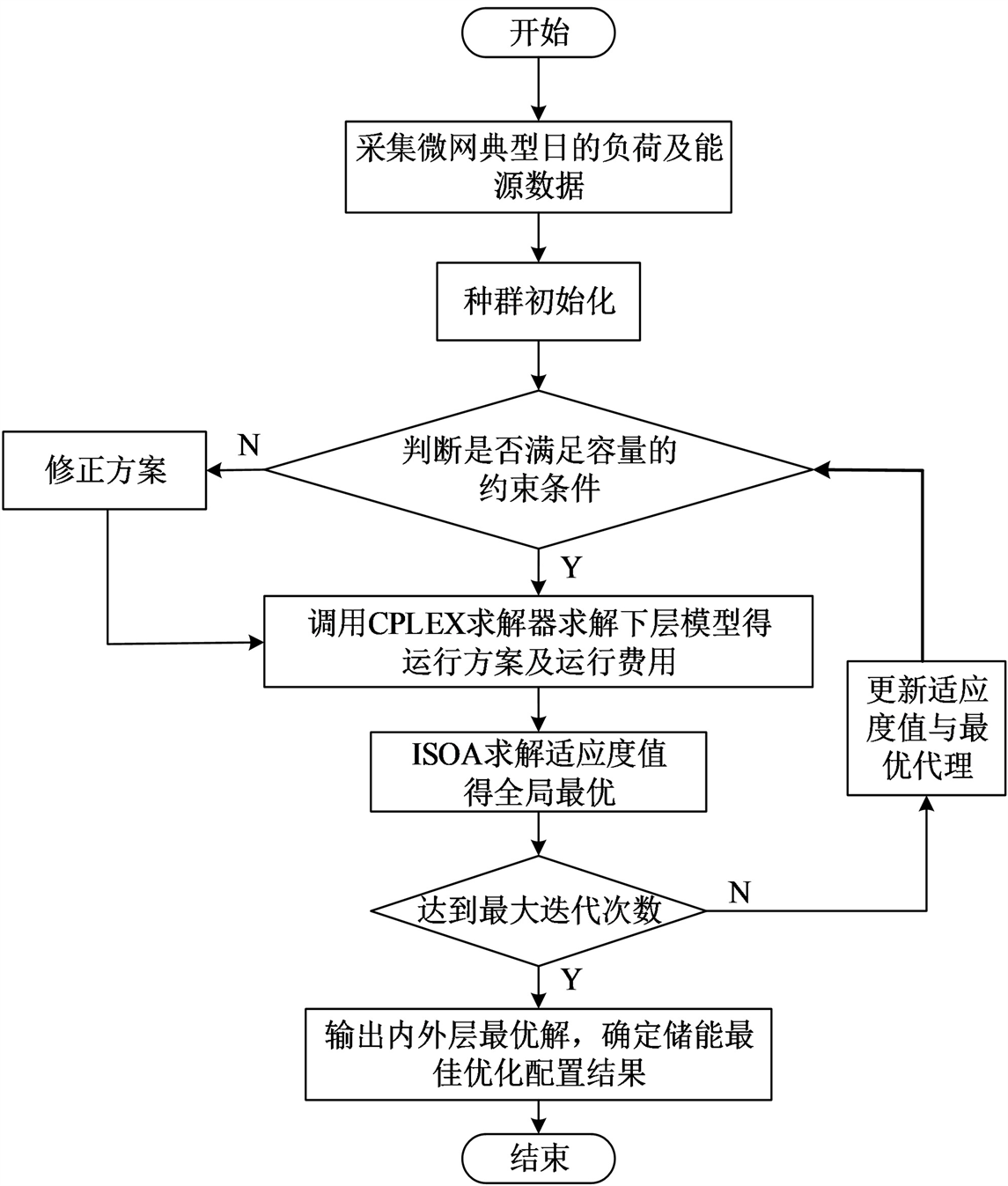
Figure 2. Flow chart for solving the two-layer model
图2. 双层模型求解流程图
2) Levy飞行
Levy飞行步长能在未知范围内搜索时,能够达到更大范围,从而加强发现者的全局搜索能力,在最优位置附近扩大范围进行搜索,避免个体陷入局部最优 [9] 。Levy分布如式
(26)
式中,λ为指数参数。采用Levy飞行的位置更新公式为:
(27)
3) 混合变异
将差分变异和莱维飞行策略引入最优个体位置更新中,利用判定因子n对最优海鸥个体位置进行混合变异扰动与更新,两种策略结合促进算法跳出局部最优,求解优化问题适应性更强。
(28)
n为(0, 1)范围内的随机数。基于编译后的最优个体位置不一定优于原始最优个体,采用贪婪策略,判定是否将原始解用变异解替换,当变异解的适应度值优于原始解时对其进行替换。
(29)
为进行贪婪选择后海鸥最优代理的位置。
5. 微电网优化配置求解过程
采用双层优化求解模型,采用改进的海鸥优化算法和MATLAB中的Cplex求解器联合求解,上层为改进的海鸥优化算法,下层为求解器,进行微电网储能的容量配置及优化运行,求解流程如图2所示。
6. 算例仿真分析
6.1. 实验场景及相关数据
算例采用风–光–燃–柴–储型的微电网进行优化配置,验证所提策略的可行性。SOA的初始参数
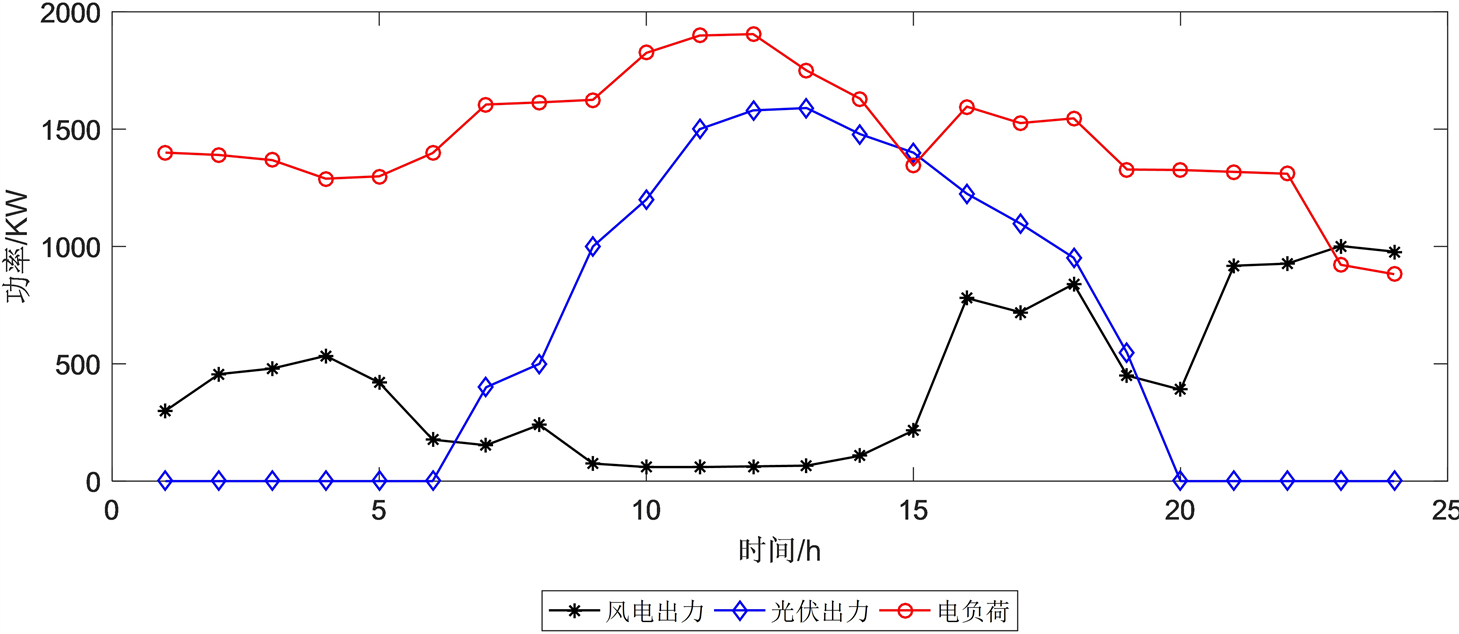
Figure 3. Microgrid loads and renewable energy output
图3. 微电网负荷和可再生能源出力
设置为:初始种群数N为80,最大迭代次数为50,风力发电、光伏发电、微型燃气轮机、柴油发电机的维护系数分别为0.0296、0.00969、0.0059、0.0128。微电网的风电、光电、和负荷的典型日出力如图3所示。
本章微电网采用的分布式电源维护系数及储能系统电池参数如表1所示 [10] 。
微网运行过程中设备产生的污染气体主要包括CO2、SO2、NOx,与其相对应的污染物排放系数、处理成本及罚款如表2所示。

Table 2. Pollution emission coefficient and treatment penalty cost
表2. 污染排放系数及治理惩罚成本
为验证所提策略有效性,分析考虑寿命损耗成本的前提下需求响应对储能优化配置结果的影响,设置以下场景进行对比:
场景1:不考虑需求响应进行系统的优化配置;
场景2:考虑需求响应进行系统的优化配置。
6.2. 算例结果分析
6.2.1. 测试函数的分析验证
通过对海鸥优化算法引入混沌反向学习和随机混合变异策略进行改进后,该算法的收敛速度和精度均得到提升。为验证ISOA改进策略的有效性,采用CEC标准测试函数中的三个标准测试函数进行测试,并将测试结果与海鸥优化算法(SOA)、灰狼优化算法(GWO)和鲸鱼优化算法(WOA)进行对比,算法的最大迭代次数Tmax = 1000,种群数N = 30。标准测试函数的三维立体图及寻优曲线如图4所示。
从图4可以看出,本文提出的ISOA与其他算法相比收敛速度和收敛精度均具有一定提升,跳出局部最优的能力更强。
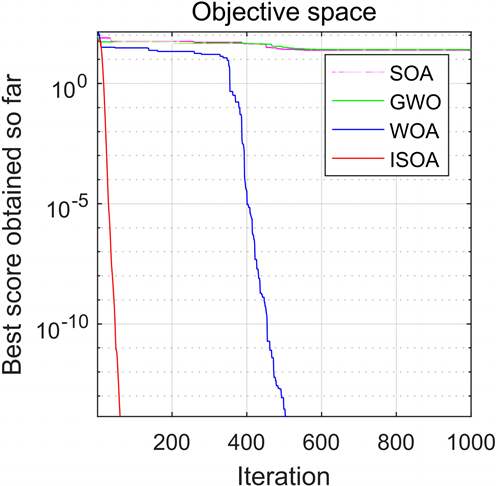
Figure 4. Function tests optimizes curves
图4. 函数测试寻优曲线
6.2.2. 算例分析验证
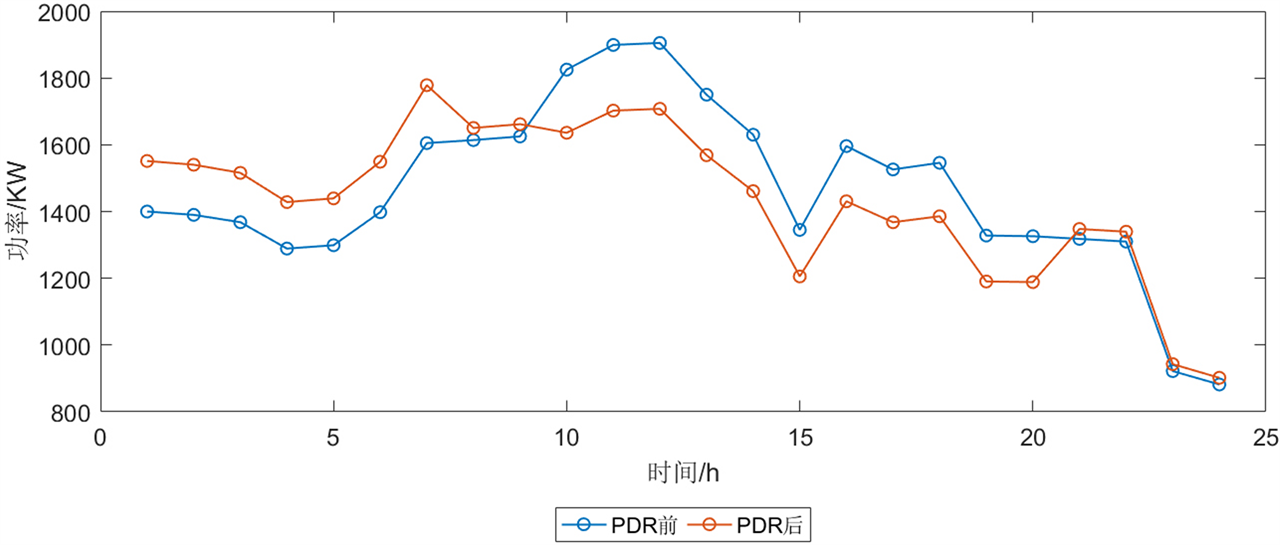
Figure 5. User load curve before and after the demand response
图5. 需求响应前后用户负荷曲线
未考虑价格型需求响应前其购电价格为0.7元/kWh,优化后的电价如下表3所示:

Table 3. Time-of-use electricity price
表3. 分时电价
各电源出力情况如图6和图7所示。
1) 负荷曲线分析
通过图5和表3可知,在考虑PDR后,通过分时电价机制引导高峰期用户负荷弹性下降转移到波谷。图中,场景1的负荷的波动较大,在价格激励下负荷转移效果明显。用户通过在电价低谷期提升用电量,在电价高峰期降低用电量,减轻微网在高峰时段的供应压力,用户主要在9:00~21:00采取减少负荷的行为,在0:00~9:00和21:00~24:00时段增加负荷的行为,将高峰时段的负荷需求转移到平谷时段,使此时的弃风弃光量降低,消纳系统盈余电量,缓和系统负荷曲线的峰谷波动。
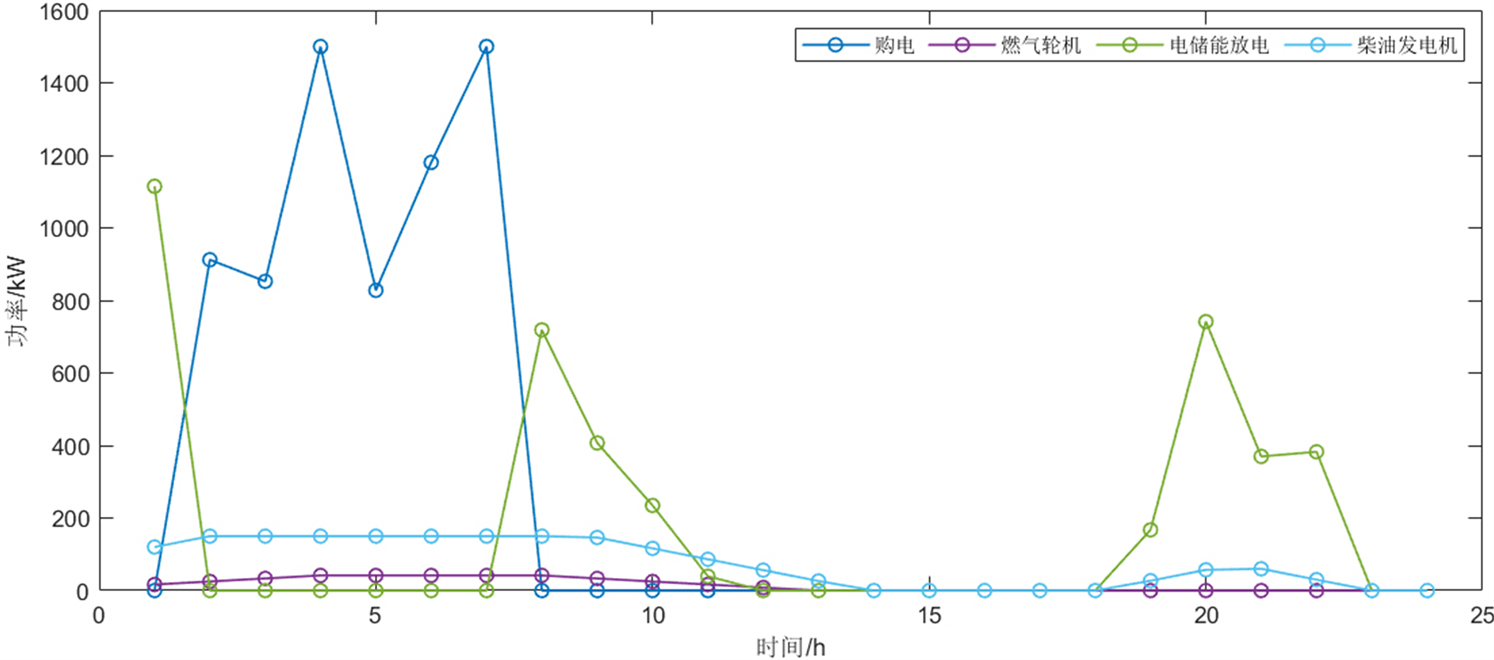
Figure 6. Scenario 1 output of each power unit
图6. 场景1各发电单元出力情况

Figure 7. Scenario 2 output of each power unit
图7. 场景2各发电单元出力情况
由图6和图7可知,在场景1和场景2两种的情况下,当考虑需求响应后,用户通过在平谷期增加用电量,消纳多余电量,在高峰期减少用电量,缓解用电负担。微网电价低时段向电网购电购电,电价高时储能放电。微型燃气轮机、柴油机和储能系统进一步得到整合,协同出力,缓解供电压力,提高系统经济性及环保性。
2) 成本分析对比
两种场景优化结果如表4所示。

Table 4. Comparison of optimization results in scenario 1 and scenario 2
表4. 场景1和场景2优化结果对比
由优化结果可知,在考虑需求响应的情况下,系统的运行成本整体较低,但由于负荷需求调整至低平谷,微型燃气轮机和柴油机得到充分利用,出力增加,随之的燃料成本与环境治理成本有一定程度的增加,但系统整体的综合成本降低5.87%,负荷变化较之前变化差距减小,电池的寿命损失成本也相应的降低,因此考虑电池寿命和需求响应对微网进行优化配置更具有经济性。
7. 结论
本文以风–光–燃–柴–储型微电网为研究对象,针对微电网的优化配置问题,提出考虑价格型需求响应,采用改进的海鸥优化算法,在保证微电网的各项约束下,进行微电网的容量优化配置求解,结论如下:
1) 文中考虑价格型需求响应后,通过分时电价能够有效调节用户的用电行为,减轻微网用电高峰的供电压力,并降低成本。
2) 文中采用的ISOA算法教传统的SOA算法具有更好的收敛速度与精度,寻优时更易获得全局最优解。
采用本文所提的基于需求响应的双层优化配置模型,能够有效降低系统总成本,具有更高的经济性。