1. 引言
煤矿开采工作中常遇到一些如断层、陷落柱、采空区等地质体的干扰。在陷落柱比较发育的地区,其是不容忽视的灾害性地质异常体,煤系地层中陷落柱的存在会破坏煤层的连续性,影响煤巷围岩的稳定性,影响巷道的掘进和煤矿的开采,还可能形成一种特殊的导水通道,引发突水等安全事故,严重时可能造成人员伤亡 [1] [2] 。精准探明掌子面前方陷落柱的位置、范围与形态等参数尤其重要。而实际煤层的物性条件复杂,导致实际勘探的波场具有复杂性与不确定性。因此通过数值模拟研究含陷落柱煤系地层中的反射槽波传播规律具有重要意义。
2011年杨思通提出反射Rayleigh型槽波的SV分量可以作为超前探测陷落柱的有效波 [3] 。2012年王勃等通过二维正演模拟分析了掌子面前方存在陷落柱时的地震波场特征,总结出基于绕射偏移的陷落柱边界探测方法 [4] 。目前,诸多学者的研究都是基于弹性各向同性的理想模型条件进行数值模拟,而实际地层具有黏弹性质,导致数值模拟结果与实际煤矿探测数据存在误差 [5] 。苑春方等 [6] 、刘瑞珣 [7] 发现Kelvin-Voigt黏弹性介质模型相比其他黏弹模型考虑了介质对地震波能量的损耗,使用Kelvin-Voigt模型更加符合地下介质是粘弹性质的实际情况。
目前基于黏弹性质的槽波超前探测理论研究很少。因此,笔者在前人的研究基础上,基于黏弹三维一阶速度–应力方程,采用交错网格高阶有限差分方法进行槽波超前探测陷落柱的三维数值模拟,分析掌子面前方存在陷落柱时的波场特征与反射槽波的传播规律。
2. 原理
2.1. 槽波超前探测原理
超前探测指的是探测掘进巷道前方一定距离内的构造情况。超前探测的测线布置与侧帮探测相似,是布置在巷道侧帮煤壁上,检波器安装在浅孔内或锚杆头上,或者侧帮打深孔,在深孔内安装多个检波器。不同之处在于,为提高效率、减少探测施工对掘进工作的影响,超前探测的炮数较少,有时仅在测线的两端布置炮点 [8] 。
槽波是一种仅沿煤层传播的制导波,具有传播距离远、能量强、波形特征易于识别、携带地质信息丰富的特点,且具有明显的频散特征。槽波大部分能量不向围岩辐射,携带大量地质构造信息,加之煤层的波导性,槽波被应用于超前探测。图1为槽波超前探测原理图,槽波在沿超前探测方向传播过程中遇到陷落柱(存在波阻抗差异)时会产生反射槽波,对其进行处理、分析与解释,进而实现对掌子面前方地质构造异常区域的槽波超前探测 [9] [10] 。
2.2. 三维黏弹性波动方程
使用vx、vy、vz变量表示位移的一阶导数,减少位移二阶导数的使用,简化整个计算过程。在没有受到外力影响或外力消失之后,根据Kelvin-Voigt模型,可获得三维黏弹一阶速度–应力方程 [11] :
(1)
式中,
、
、
为正应力;
、
、
为剪应力;
为弹性矩阵,i、j分别为矩阵的行号和列号;
为黏滞矩阵;t为传播时间,单位s;vx、vy、vz分别为质点沿x、y、z方向的振动速度,x、y和z分别代表三维空间中的平面水平方向、平面竖直方向和纵向。
2.3. 有限差分方法
有限差分就是将求解区域进行网格划分,使用有限的网格节点取代连续的求解域,利用微商与差商的近似关系,将描述地震波传播的微分方程转化为差分方程。差分离散主要分两种,其一是将单变量的二阶波动方程直接转化为时间空间的二阶中心差分进行离散求解;其二是将用位移表示的二阶波动方程转化为用应力及质点速度表示的一阶方程组,即一阶速度–应力方程,然后使用应力和速度的交错网格进行离散求解 [12] 。低阶近似、规则网格的有限差分方法具有强频散和低精度的缺点 [13] ,为保证计算精度,本文使用交错网格高阶有限差分方法对公式1进行离散化。2L阶空间差分精度、二阶时间差分精度三维各向同性介质交错网格高阶有限差分离散方程 [11] ,如下:
(2)
式中,Δt为时间差分间隔,上标n表示n Δt时刻,
表示n + 1/2,
表示n − 1/2;i、j、k表示空间差分格点位置;
等为差分算子。
2.4. 吸收边界与稳定性条件
地震波正演数值模拟不仅要考虑数值算法的构造,还需要考虑边界条件与稳定性条件。完美匹配层(Perfect Matched Layer,简称PML)原理为:将求解对象的变量分为两个部分,平行于边界的分量和垂直于边界的分量,人为在计算区域四周加上完全匹配层,可以充分的吸收边界反射,且其可以在短时间内吸收衰减沿人工界面法向的各类平面波,从而降低人工界面所产生的各类反射波,除此之外,和人工界面彼此平行的平面波不会发生衰减。在理论和模型算例上证明该方法可以很好吸收来自各个方向、各种频率的波 [14] 。
为避免产生较大的数值频散,在数值模拟时,时间步长、空间步长以及物理参数的选取均需满足差分计算的稳定性要求 [15] 。根据傅里叶分析,得到交错网格有限差分法各类差分精度的稳定性条件,如下 [11] :
(3)
式中:vp指介质纵波速度,Δx、Δy和Δz分别为x、y和z方向的网格步长,
指差分系数。
3. 模型与参数
模型在X、Y、Z方向的大小分别为300 m × 100 m × 25 m,图2、图3分别是三维含陷落柱煤系模型的XOY切面和XOZ切面,其中X方向为平行巷道方向,Y方向为垂直巷道方向,Z方向为垂直方向。模型网格dx、dy、dz分别为1 m × 1 m × 0.25 m,煤厚5 m。煤巷长度150 m,宽度4 m,高度4 m,起点坐标为(10, 48, 10.5)。掌子面位于X = 160 m处,陷落柱中心点坐标为(240, 50, 12.5),半径D = 20 m。使用主频为150 Hz的雷克子波作为激发震源,延迟时间为20 ms,时间的采样间隔为0.05 ms,震源坐标为(110, 54, 12.5)。检波器与震源同一水平线布置,布测于X方向80~160 m,道间距1 m,共81个检波点。根据相关文献中煤层和围岩物性参数常见值的范围划分 [16] ,设计模型各物性参数如表1所示,煤层的顶底板岩性参数一致,巷道赋予空值。
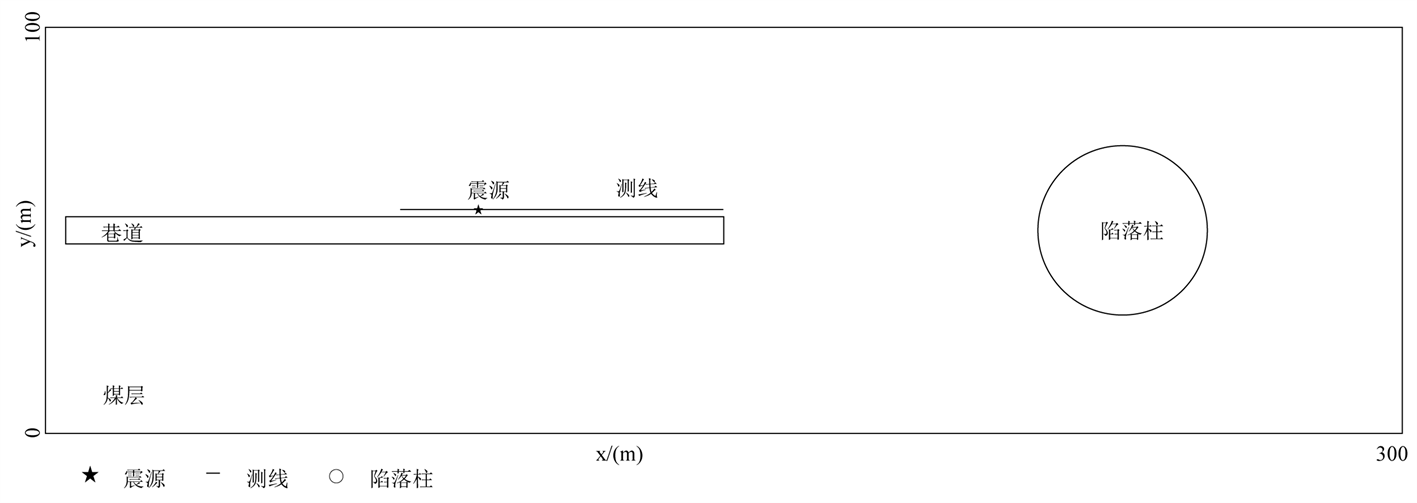
Figure 2. 3D coal series model XOY section
图2. 三维煤系模型XOY切面
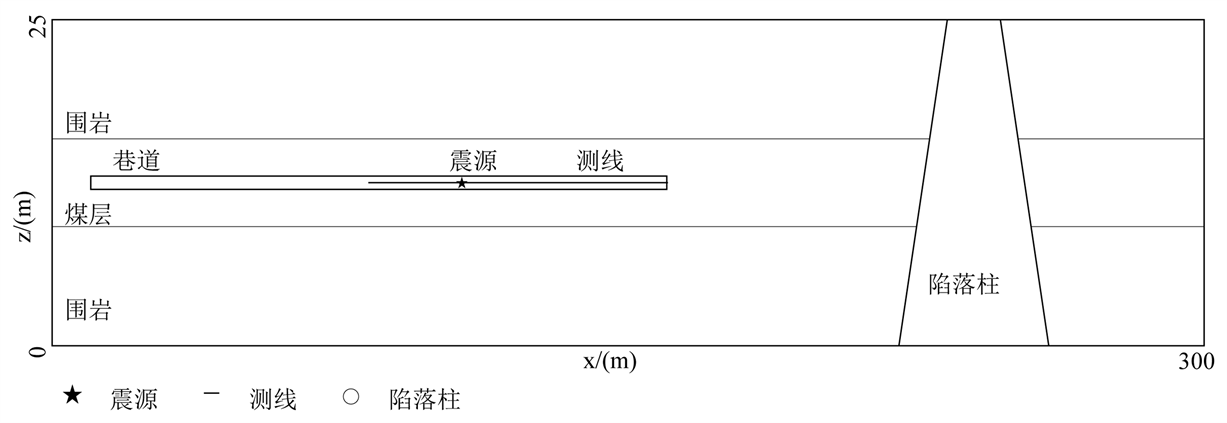
Figure 3. 3D coal series model XOZ section
图3. 三维煤系模型XOZ切面
4. 正演模拟与分析
4.1. 波场快照
图4为正演模拟的X分量40 ms、80 ms、120 ms与160 ms在Z = 12.5 m的波场快照。图4(a)为传播时间40 ms,震源激发后,产生纵波、横波,体波传播速度快,向超前方向传播率先经过掌子面,一部分体波在掌子面发生反射。图4(b)为传播时间80 ms,直达纵波已经过陷落柱,且在陷落柱左界面(靠近掌子面一侧)产生反射波和透射波,反射波被直达横波干扰,波形不明显,陷落柱体内的透射波能量有衰减,直达纵波的波形变化较小,部分速度较快的波已传播至模型右侧壁(X = 300 m);直达横波紧跟直达纵波;在体波传播过程中,纵波与横波的SV波相互叠加、干涉形成Rayleigh槽波,与体波相比,直达Rayleigh槽波能量较大、速度较慢;各直达波在掌子面处形成的系列掌子面反射波已沿巷道向后传播扩散。图4(c)为传播时间120 ms,直达横波经过陷落柱,透射进陷落柱的波能量有衰减,波形有变化。图4(d)为传播时间160 ms,反射横波到达掌子面;直达Rayleigh槽波传播至陷落柱,在陷落柱界面产生反射波和透射波,透射入陷落柱的波能量衰减大,波形有明显变化,波形不连续;掌子面反射波沿巷道向后已传播至巷道中部;地震波传播至巷道头时,亦形成了巷道头反射波。
 (a) 40 ms
(a) 40 ms 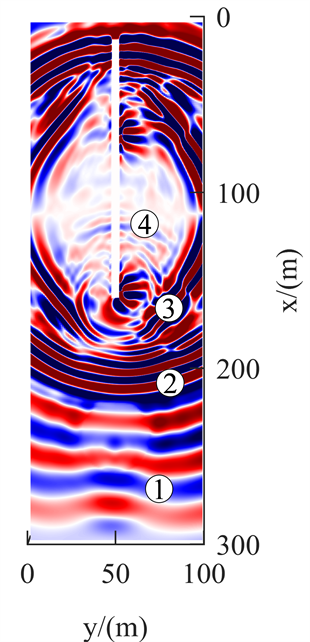 (b) 80 ms
(b) 80 ms  (c) 120 ms
(c) 120 ms 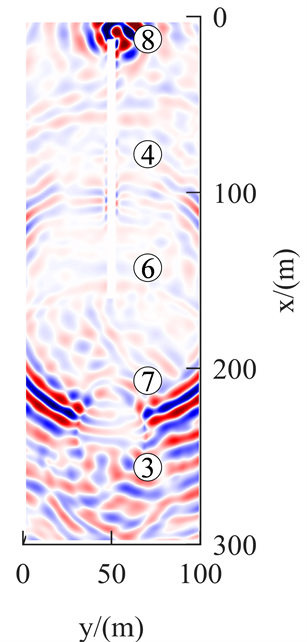 (d) 160 ms
(d) 160 ms
Figure 4. X-component wave field snapshot (In the figure: wave group 1—direct longitudinal wave, wave group 2—direct transverse wave, wave group 3—direct in-seam wave, wave group 4—reflected wave on the palm surface, wave group 5—reflected longitudinal wave, wave group 6—reflected transverse wave, wave group 7—reflected in-seam wave, and wave group 8—reflected wave at the tunnel head)
图4. X分量波场快照(图中:波组1——直达纵波,波组2——直达横波,波组3——直达槽波,波组4——掌子面反射波,波组5——反射纵波,波组6——反射横波,波组7——反射槽波,波组8——巷道头反射波)
图5为正演模拟的Y分量40 ms、80 ms、120 ms与160 ms在Z = 12.5 m的波场快照。观察发现,Y分量地震波传播的波场类似于X分量。图5(a)为传播时间40 ms,震源激发产生纵波、横波。图5(b)为传播时间80 ms,直达纵波已经过陷落柱,透射入陷落柱的波能量有衰减,遇陷落柱波形有变化;在传播过程中,SH波相互干涉形成Love槽波。图5(c)为传播时间120 ms,直达横波已传播至陷落柱,透射进陷落柱的波能量衰减小,波形有变化。图5(d)为传播时间160 ms,直达Love槽波传播至陷落柱,产生反射Love槽波,透射入陷落柱的波能量衰减小,波形变化不明显;反射横波到达掌子面;掌子面反射波沿巷道向后传播至巷道中部。
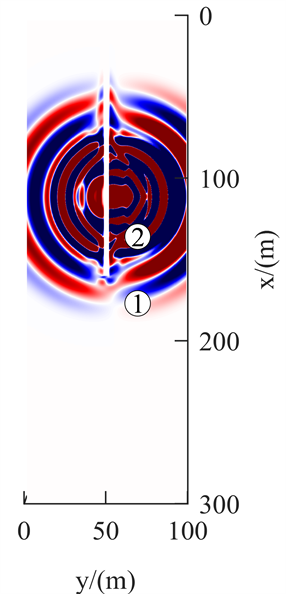 (a) 40 ms
(a) 40 ms  (b) 80 ms
(b) 80 ms 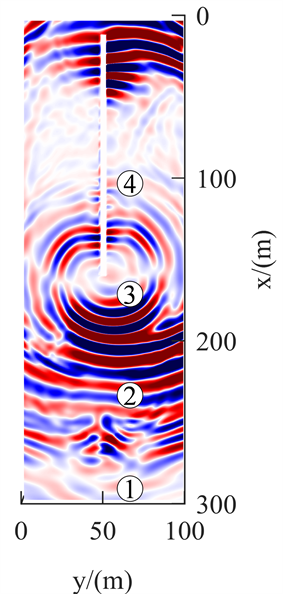 (c) 120 ms
(c) 120 ms 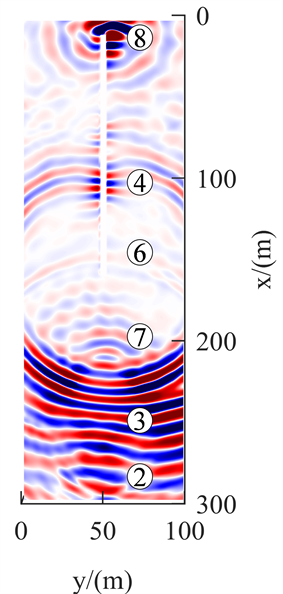 (d) 160 ms
(d) 160 ms
Figure 5. Y-component wave field snapshot
图5. Y分量波场快照
图6分别为正演模拟的Z分量40 ms、80 ms、120 ms与160 ms在Z = 12.5 m的波场快照。观察发现,Z分量中地震波的传播与X分量相似。图6(a)为传播时间40 ms,震源激发产生纵波、横波。图6(b)为传播时间80 ms,直达纵波已经过陷落柱,透射入陷落柱的波能量增大,波形变化明显;纵波与横波的SV波在传播过程中相互干涉形成Rayleigh槽波。图6(c)为传播时间120 ms,直达横波传播至陷落柱,透射入陷落柱的波能量衰减较小,波形有变化。图6(d)为传播时间160 ms,反射纵波已快传播至巷道中部;反射横波到达掌子面;直达Rayleigh槽波在陷落柱界面波形不连续,产生的反射Rayleigh槽波紧跟反射横波。
 (a) 40 ms
(a) 40 ms 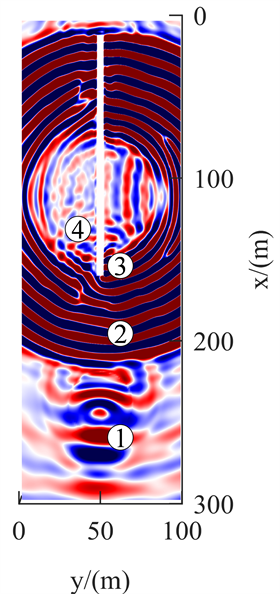 (b) 80 ms
(b) 80 ms 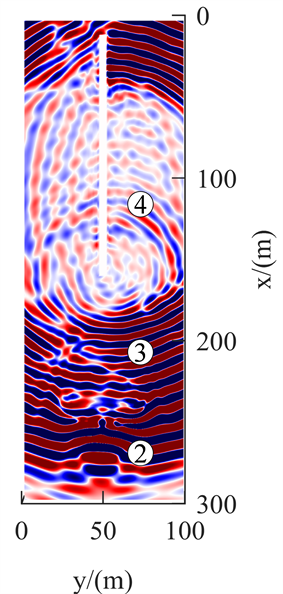 (c) 120 ms
(c) 120 ms 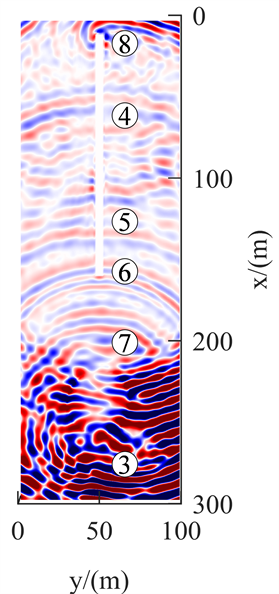 (d) 160 ms
(d) 160 ms
Figure 6. Z-component wave field snapshot
图6. Z分量波场快照
不同分量上地震波受陷落柱的影响不同。X分量的直达Rayleigh槽波受陷落柱影响较大,波形不连续,陷落柱的边界范围明显可见;遇陷落柱产生的反射Rayleigh槽波波形模糊。Y分量的直达Love槽波受陷落柱影响较小;遇陷落柱产生的反射Love槽波波形较清晰。Z分量的直达Rayleigh槽波受陷落柱影响较大;反射Rayleigh槽波波形较清晰。
4.2. 地震记录
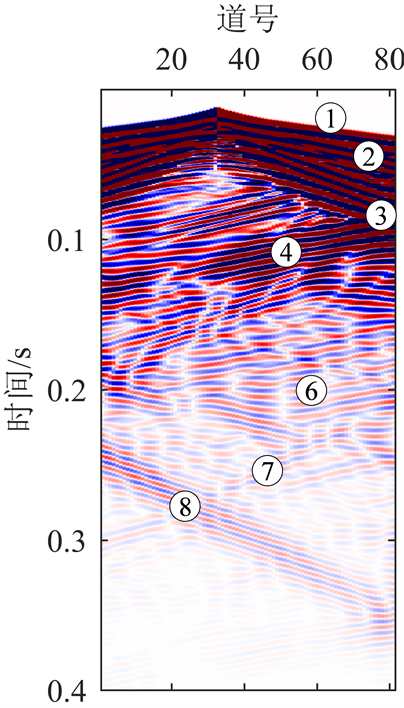
图7为合成地震记录的三分量图,图中横轴为检波器编号,纵轴为传播时间。结合波场快照和波的时距曲线特征,图7各分量上按被接收的时间顺序可识别出:直达纵波、直达横波、直达槽波、掌子面反射波、反射纵波、反射横波、反射槽波和巷道头反射波,与波场快照中所识别的波组相对应。图7(a)为X分量地震记录,反射Rayleigh槽波在能量较大掌子面反射波的干扰下难以识别,同相轴较模糊。图7(b)为Y分量地震记录,反射Love槽波能量较大,与其他波列在时间轴上间隔大,波列易识别。图7(c)为Z分量地震记录,陷落柱的各反射波波组连续性好,反射Rayleigh槽波能量较小,与掌子面反射波振幅大小相似,波列较易识别。
震源激发后,沿超前方向传播的体波和槽波遇到陷落柱表面产生了振幅较弱的反射纵波和反射横波,在X与Z分量产生了能量较小的反射Rayleigh槽波,在Y分量产生了振幅较强、同相轴明显的反射Love槽波。因此可以利用反射Love槽波超前探测陷落柱。
 (a) X分量
(a) X分量  (b) Y分量
(b) Y分量 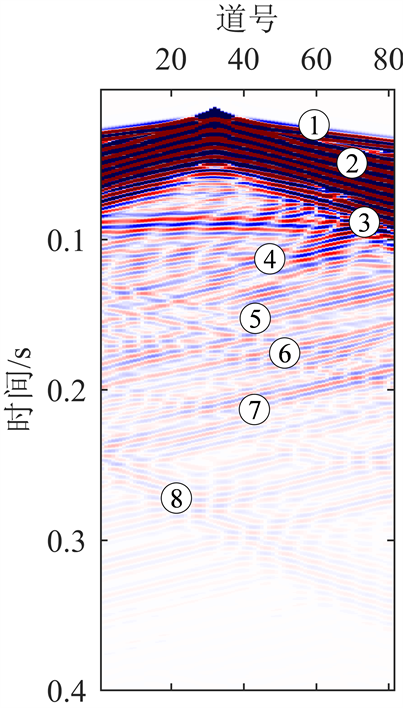 (c) Z分量
(c) Z分量
Figure 7. Three component map of seismic records
图7. 地震记录三分量图
5. 结论
通过数值模拟含陷落柱的黏弹性煤系地质模型,分析波场快照与地震记录,对槽波超前探测陷落柱得出如下结论:
1) 通过三个分量的波场快照图发现,地震波在沿超前方向传播时,遇陷落柱皆产生了反射槽波。X和Z分量的Rayleigh槽波受陷落柱影响大,Y分量上Love槽波受陷落柱影响较小。
2) 三分量地震记录上,X与Z分量接收的反射Rayleigh槽波能量较小,Y分量接收到的反射Love槽波能量较大,同相轴明显。建议利用Y分量的反射Love槽波超前探测陷落柱。
限于篇幅,本文数值模拟模型仍不够多,后续还需建立更多模型更全面的研究陷落柱的反射槽波响应特征。