基于时间卷积网络的移栽机齿轮箱轴承退化趋势研究

Research on the Degeneration Trend of Transplanting Gear Box Bearing Box Based on Time Convolution Network

摘要: 针对移栽机齿轮箱轴承振动信号传递路径长，难以进行基于振动信号的轴承退化趋势预测问题，以基于振动信号进行机器学习的轴承退化趋势预测算法研究，可实时监测齿轮箱退化趋势，最大程度减少损失。利用时间卷积网络通过不同尺寸的卷积核对轴承振动信号进行卷积，实现对历史信息的特征提取；其次通过链式结构实现网络的参数共享，有效解决长时间序列下的低预测精度等问题；通过引入因果卷积、跳层连接与残差网络等结构，使得其在CNN与RNN的基础上能够有效解决梯度消失或爆炸等问题，捕捉序列的长期退化趋势与轴承振动信号间的非线性关系，由此建立齿轮箱轴承退化趋势预测模型。进行实验探究时间卷积网络模型对退化趋势预测准确率的影响并验证其有效性。研究结果表明，基于在不同尺寸、不同故障类型、不同传感器采集到的振动信号对齿轮箱轴承退化趋势都具有显著的预测效果，满足设计要求。

Abstract: For the long way to transmit the vibration signal of the gear box of the transplanted machine, it is difficult to conduct the prediction of the bearing degradation trend based on the vibration signal. Reduce loss to the greatest extent. Using time convolutional networks to convolve the bearing vi-bration signals through convolution kernels of different sizes to achieve the characteristics of his-torical information to extract the characteristics of historical information; secondly, the parameter sharing of the network through the chain structure can effectively solve the problems of low predic-tion accuracy under long sequence; by introducing the structure of causal convolution, jumping layer connection and residual network, it enables it to effectively solve the problems such as gradi-ent disappearance or explosion on the basis of CNN and RNN. Relations, thereby establishing a pre-dictive model of gear box bearing trend. The effect of experimental exploration of the accuracy of the accuracy of degradation trend predicts and verifies its effectiveness. The results of the study show that the vibration signals collected by different sizes, different faulty types, and different sen-sors have significant predictive effects on the trend of the bearing of the gear box to meet the design requirements.

1. 引言

轴承是农机齿轮箱内的旋转部件，农机齿轮箱在实际工作过程中轴承会产生周期性运动，轴承的运动不仅会受轴承故障的影响，还会由于温度、噪声的不同而有所差异，同时轴承振动信号的变化通常隐藏在大量的背景噪声中。因此基于轴承振动信号的农机发动机性能退化趋势逐渐成为业内重要的研究方向。目前国内外针对退化趋势的研究主要围绕轴承数据预处理、性能退化的有效表征及预测模型的构建等方面展开。其中基于大数据模拟的农机发动机性能退化趋势的预测方法尤为热门，即在轴承运行过程中的构建基于AI的实时状态监测模型来预测其工作状态，进而实现定位故障点及退化趋势预测的目的。

基于AI的退化趋势预测模型主要分为两类：基于机器学习和基于深度学习的预测模型。而以这两种为代表的数据挖掘方法，用于发动机故障趋势预测的智能算法已进行多年研究。当前常见的智能算法包括支持向量回归(SVR)、差分整合移动平均自回归(ARIMA)模型、长短期记忆网络(LSTM)、决策树和逻辑回归等，较多用于研究齿轮箱轴承退化趋势预测，但考虑到农机发动机振动信号采样频率高及其工况的复杂性，难以实现在实际应用中准确、快速地对农机发动机的高精度退化趋势预测，因此本文拟开展基于机器学习的水稻钵苗移栽机齿轮箱轴承退化趋势预测研究。

国内外关于轴承退化趋势预测问题上取得了许多成果。Mahamad等人最早提出了将均方根和峭度作为人工神经网络(ANN)的输入特征的发动机退化趋势预测方法，然后将寿命百分比进行归一化操作后作为整个退化趋势模型的输出，由此能有效预测轴承失效的时间点 [1] 。Gebraeel等人使用了具有反馈性质的BP神经网络构建新型轴承退化趋势预测模型，并对基于振动信号计算农机发动机的回归预测模型的参数进行实时更新，来对移栽机齿轮箱轴承参数的实时预测实现 [2] 。Maior等人考虑到SVM在非平稳的移栽机齿轮箱轴承振动信号上表现不佳的问题，提出基于EMD和SVM的齿轮箱轴承退化趋势预测模型，结果表明比单一的SVM性能更佳 [3] ；奚立峰等人提出了一种利用自组织映射和BP神经网络两种算法模型用来筛选时域、频域等特征，并据此建立了剩余寿命预测模型，实验结果证明该方法在剩余寿命预测上的预测精度优于基于L10寿命估计方法 [4] 。张鑫等人提出先通过BP神经网络来预测轴承寿命分布的分布情况，然后再基于维修窗进行维修决策的指定，克服基于阈值的轴承维修决策模型代价成本过高的缺点，能够在降低维修成本的同时提升轴承寿命预测的精度 [5] 。李浩平等人提出一种结合了自适应遗传算法和广义回归神经网络(AGA-GRNN)神经网络的新型刀具使用寿命预测方法，用以解决传统的BP神经网络由于参数众多所导致的模型计算复杂度过大等缺陷，此法在参数优化效率和预测精度上较优 [6] 。申中杰等人针对单一变量无法表征出信号中的所有信息等不足，提出了一种基于多变量SVM和相对特征的趋势预测方法 [7] 。徐继亚等人使用了KPCA提取轴承振动信号的T2和SPE等统计特征，在进行信息粒子化后将上述统计特征作为SVM的输入进行并进行有效的滚动轴承退化趋势和回归预测 [8] 。

本文的研究目的旨在结合特征工程与智能预测算法对基于振动信号的水稻钵苗移栽机齿轮箱轴承的退化趋势进行预测，同时探索准确率更高、适应性更强的退化趋势预测方法，为合理地制定维修策略、建立更加科学的维修体制提供辅助性的依据。

2. 理论基础

通过分析轴承故障诊断的研究现状进而得出诊断思路。所用方法采用信号的分析与特征提取与辨识分类两个过程。通用算法思路从信号时域或者频域分析，借助信号分析方法与数据驱动技术以及机器学习手段实现。

为确保诊断结果的高效性，算法结构的组合优化成为首要选择，在特征提取阶段对信号的分析研究需要专业的技术要求，难度较大。专家经验也受信号提取的优劣影响，组合研究存在算法的实用性问题。而将信号特征提取、数据降维与输出分类统一起来，直接作用于信号的诊断研究，这成为卷积结构端到端模式的优越性。由于农机发动机不同传感器采集到的振动信号是一维的不定长时序型数据，因此可以使用时间卷积网络提取轴承振动信号的深层特征并根据滑动窗口的思想，实现基于水稻钵苗移栽机齿轮箱轴承振动信号的不同健康状态的性能退化趋势预测。

2.1. 基本网络结构

虽然RNN在处理序列问题上表现不俗，但在实际应用中，RNN由于自身结构的缺陷，使得RNN一次只能处理一个步长的序列数据，后一步的数据必须等模型处理完前一步才能进行处理。因此这也让RNN不能像CNN一样直接对数据进行批量并行处理，在任务完成前需要保存所有中间步骤的结果，而这也意味着RNN模型的时间复杂度和空间复杂度极高 [9] 。时间卷积网络结构如下图1所示，由于CNN在处理图像型数据时，本质上将图像视为一个二维矩阵进行后续处理。将这种思想运用到时间序列问题

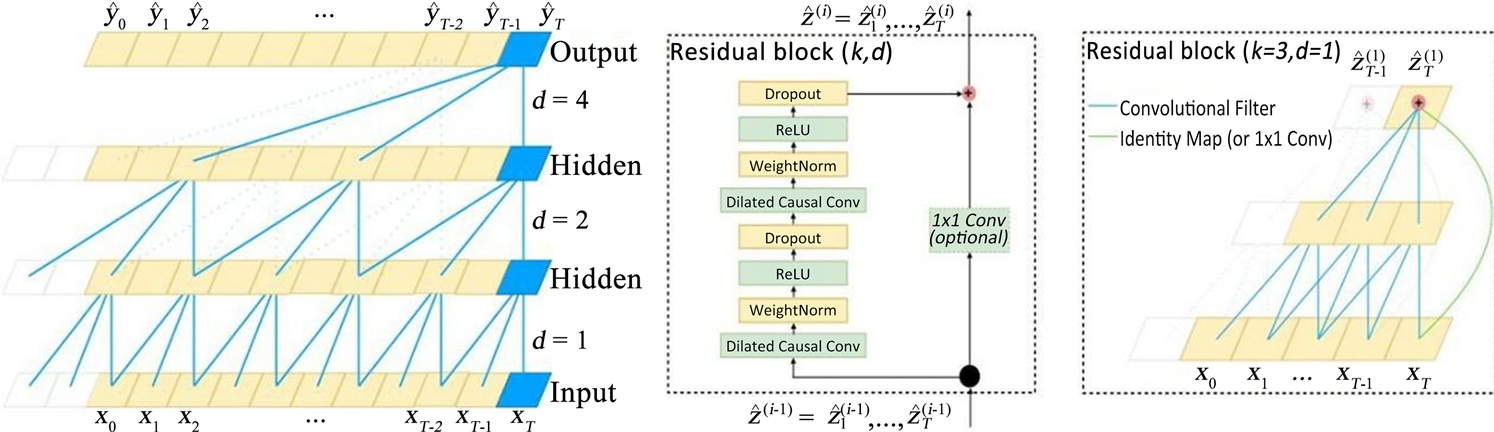(a) 因果空洞卷积过程 (b) 残差块结构； (c) TCN中残差块连接

Figure 1. Overall structure diagram of TCN

图1. TCN的整体结构图

上，可以通过将时间序列视为一个一维向量再输入至多层网络中，获得足够大的感受野。得益于卷积神经网络能够并行处理大规模样本数据的优势，时间卷积网络能够通过并行处理的方式极大地降低模型的时间复杂度，这也是时间卷积网络的基本思想 [10] 。

2.2. 时间卷积神经网络模型

时间卷积网络主要由因果卷积、空洞卷积以及残差块等结构组成。下面将对网络架构中的上述三个核心组成部分进行说明。

1) 因果卷积

由于CNN本身并不具备处理序列型数据的能力，因此考虑通过引入因果卷积的方式将序列问题转化为：根据 $x_1,x_2,\cdots ,x_t$ 预测 $y_1,y_2,\cdots ,y_t$ 。假设存在序列 $X=\left(x_1,x_2,\cdots ,x_T\right)$ ，定义滤波器组 $F=\left(f_1,f_2,\cdots ,f_K\right)$ ，则在 $x_t$ 处的因果卷积为：

${\left(F^{*}X\right)}_{(}{{}_{x_t}}_{)}={\displaystyle \underset{k=1}{\overset{K}{\sum }}{f}_k{x}_{(t-K+k)}}$ (1)

因果卷积过程如下图2所示：

Figure 2. Causal convolution diagram

图2. 因果卷积示意图

其中第一层隐藏层中最后一个隐藏节点 $h_t^1$ 与输入层的最后两个节点 $x_{t-1},x_t$ 及滤波器组 $F=\left(f_1,f_2\right)$ 的关系为：

$h_t^1=f_1{x}_{(t-1)}+f_2{x}_t$ (2)

由此可知，因果卷积有如下两个特点：

a) 仅考虑历史信息，不考虑未来信息。在给定观测序列 $x_1,x_2,\cdots ,x_t$ 的条件下，若需要预测 $y_t$ 则只能用到已观测到的序列 $x_1,x_2,\cdots ,x_t$ ，而不能考虑使用在t时刻未曾观测到的序列 $x_{t+1},x_{t+2},\cdots$ 。

b) 隐藏层的层数与序列涉及到的时间跨度成正相关。以上图为例，第三层隐藏层的最后一个节点h₃与输入的 $x_{t-2},x_{t-1},x_t$ 等三个节点相关，而输出层的最后一个节点y与输入的 $x_{t-3},x_{t-2},x_{t-1},x_t$ 等四个节点相关。

2) 空洞卷积

传统的卷积神经网络通过池化层来获得范围更广的感受野，而池化层本质上是对矩阵进行平均或取最大值等操作，因此序列数据经过池化层后必定存在信息丢失等问题。而空洞卷积通过在传统的卷积核的基础上中引入空洞结合，以达到同时增加感受野及最大程度上保留原始信息的目的。相比于传统的卷积核，空洞卷积中存在一个重要的超参数——空洞率(Dilation Rate)，空洞率是指是卷积核的间隔数。假设存在序列 $X=\left(x_1,x_2,\cdots ,x_T\right)$ ，定义滤波器组 $F=\left(f_1,f_2,\cdots ,f_K\right)$ ，则x_t处空洞率为d时空洞卷积的计算公式为：

${\left(F_d^{*}X\right)}_{(}{{}_{x_t}}_{)}={\displaystyle \underset{k=1}{\overset{k}{\sum }}{f}_k{x}_{(t-(K-k)d}}$ (3)

因此传统CNN中空洞率等于1。空洞卷积核的示意图如下图3所示：

(a) 空洞率为1的卷积 (b) 空洞率为2的卷积核

Figure 3. Schematic diagram of a hollow convolution kernel

图3. 空洞卷积核示意图

3) 残差块

虽然卷积神经网络能够提取多层次的特征，但不同层次的特征的生成往往伴随着网络层数的增加，同时越深的网络通常能够提取就越丰富的深层抽象特征信息。然而，如果希望通过提高网络深度来提高模型对于抽象特征的挖掘及表达能力，极易可能导致网络在反向传播更新参数时产生梯度消失或爆炸抑或是网络退化等现象。针对梯度消失或爆炸等问题，目前业界常用的方法是通过将网络权重参数初始化为正态分布以及使用批正则化(Batch Normalization, BN)层解决；网络层数过多所导致的退化问题的表现是随着网络层数增加，在训练集上的准确率趋于饱和甚至可能会产生下降的现象，下图4是一个网络退化的例子，20层的网络比56层的网络表现更好 [11] ：

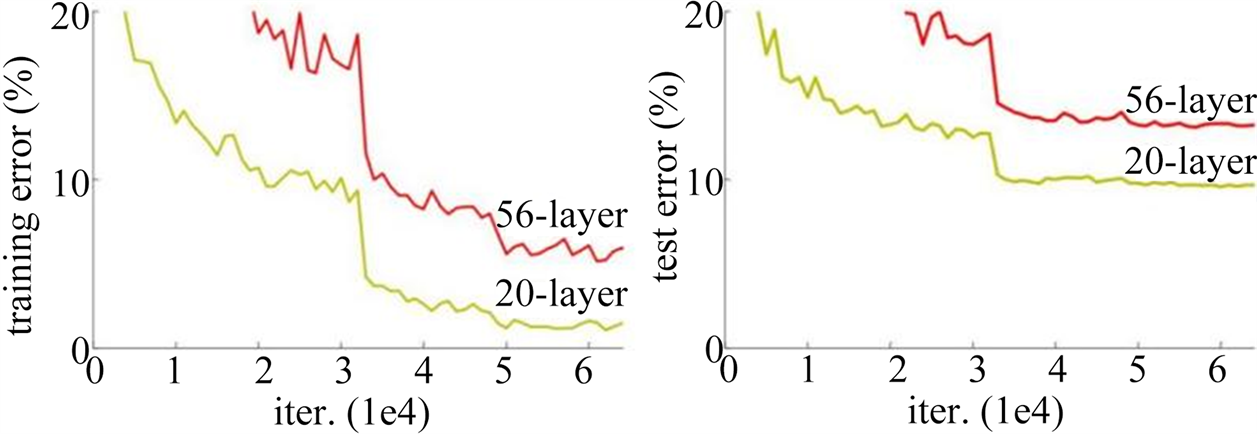
Figure 4. Diagram of network degradation

图4. 网络退化示意图

这是由于较多层网络的解空间包含了较少层网络的解空间，然而较多层网络的解空间必然更复杂，同时训练神经网络通常使用的是随机梯度下降策略，往往得是局部最优解而非全局最优解，进而产生了网络退化的现象。目前通常是利用残差块结构产生恒等映射进而解决网络退化的问题，不妨将网络中待拟合的函数 $H\left(x\right)$ 令为 $H\left(x\right)=F\left(x\right)+x$ ，此时可将对恒等映射的学习转换为学习一个残差函数 $F\left(x\right)=H\left(x\right)-x$ ，而 $F\left(x\right)=0$ 时即可视为成立恒等映射 $H\left(x\right)=x$ 。

残差块通过两种结构(a)恒等(identity)映射：即下图5中右侧的x，也被称为短路连接；(b)残差(residual)映射：即下图5中左侧的 $F\left(x\right)$ ，实现了残差块的构造，具体结构如下图5所示：

Figure 5. Residual block structure

图5. 残差块结构

其中，短路连接通常有两种方式：

(a) 同维度( $dim\left(F\left(x\right)\right)=dim\left(x\right)$ )的恒等映射：

$F\left(x\right)=W_2\sigma \left(W_{1}x+b_1\right)+b_2,H\left(x\right)=F\left(x\right)+x$ (4)

(b) 不同维度(dim(F(x))≠dim(x))的恒等映射：

$F\left(x\right)=W_2\sigma \left(W_{1}x+b_1\right)+b_2,H\left(x\right)=F\left(x\right)+W_{s}x$ (5)

2.3. 时间卷积神经网络的训练过程

训练过程就是调节参数过程，卷积核矩阵内积和得到卷积输出。根据结构参数分析，前两层卷积采用宽卷积核与长步序处理，用于提取信号的全局信息，而后的四层可分离卷积通过细卷积核与小步序细化提取局部特征。通过多步卷积操作的时间序列数据，下采样至输出层为分类特征数据，可根据特征数据概率判别类别信息，完成TCN模型结构的训练学习。

因为时间卷积网络的研究对象是序列型数据，因此通常采用一维的卷积网络。下图6是时间卷积网络结构中使用到的因果卷积与空洞卷积：

可以看到在t时刻网络中的每一层都只依赖于上一层网络中 $1,2,\cdots ,t-1,t$ 时刻的值，体现了因果卷积中“由果索因”的特性；而网络中的每一层对上一层输出的提取，都是间隔跳跃式的，且图中空洞卷积核中的空洞率以2的指数逐层增长，因此每一层都要进行0填充处理，填充的尺寸一般为 $\left(k-1\right)d$ 。

为了有效的提高准确率，防止在特征提取流程中出现过多的信息泄露，TCN网络加强了残差连接，使输入数据可以将中间不必要的环节跳过，通过1 × 1的卷积核处理后传入到全连接层，并与残差模块提取的特征相加，作为最终的输出。下图7是TCN中的残差块结构，其中恒等映射中需要对输入序列进行1 × 1的卷积操作；而残差映射主要是需要对输入序列进行空洞卷积、权重归一化、激活及Dropout等操作以拟合残差。

当空洞率d = 1时，TCN就退化为普通的卷积神经网络(CNN)：

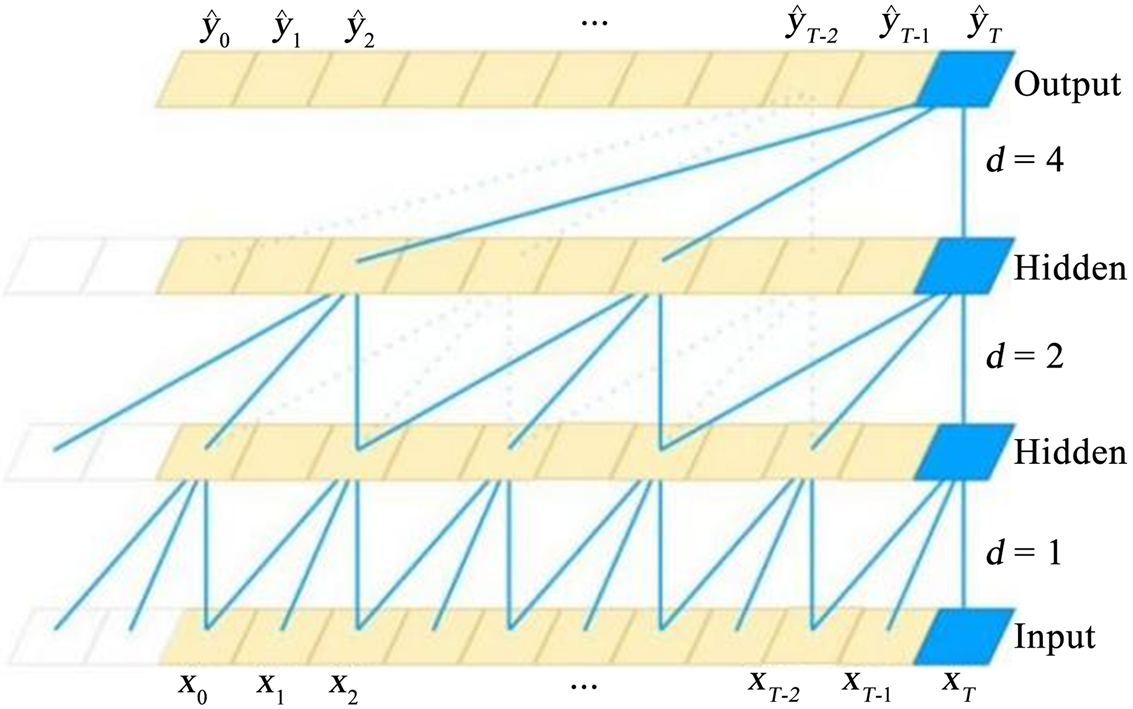
Figure 6. Causal convolution versus void convolution in TCN

图6. TCN中的因果卷积与空洞卷积

Figure 7. Residual blocks in TCN

图7. TCN中的残差块

残差连接是训练深层网络的有效方法，可将网络中不需处理的序列跳过卷积等步骤。如图8所示，TCN实例训练过程包含残差连接的1 × 1卷积操作：

该网络层的输入x与输出 $F\left(x\right)$ 的关系满足式，公式(6)：

$F\left(x\right)=D\left(x,P\right)+x$ (6)

式中：D为一系列卷积函数运算，P为卷积和的权值函数。由上式(6)可知，残差链接的结果与输入信息和权值函数的结果有关，则能保证TCN网络训练的准确度。

Figure 8. TCN instance

图8. TCN实例

Figure 9. Flowchart of bearing degradation trend prediction based on time series

图9. 基于时间序列的轴承退化趋势预测的流程图

3. 实验验证

3.1. 总体流程

本章提出了基于时间卷积网络(TCN)的水稻钵苗移栽机齿轮箱轴承退化趋势预测方法。首先，使用软硬阈值折衷的小波去噪算法对水稻钵苗移栽机齿轮箱轴承振动信号进行去噪；其次，提取去噪后的水稻钵苗移栽机齿轮箱轴承振动信号的时域以及频域特征，并将这些特征进行融合以构建水稻钵苗移栽机齿轮箱轴承振动信号的健康指数；最后，将健康指数输入至时间卷机网络中进行水稻钵苗移栽机齿轮箱轴承的退化趋势预测，并验证模型的有效性。

3.2. 结果评估

对采样频率为1.2 kHz的0.007英寸、0.014英寸、0.021英寸等故障直径，1797 rpm、1772 rpm等转速，正常、内圈故障、滚动故障等不同类型的轴承振动信号使用时间卷机网络进行退化趋势预测。将训练好的模型在测试集上进行模型验证。按照4:1的比例随机抽取样本构造训练集、及测试集，本论文滑窗尺寸选为10。由于神经网络可以极大程度地挖掘信号本身的隐藏特征，因此本章实验主要是针对去噪后的水稻钵苗移栽机齿轮箱轴承原始信号的退化趋势预测，具体结果如下图10所示：

(a) 正常驱动端轴承振动退化趋势 (b) 正常扇端轴承振动退化趋势 (c) 12 kHz、0.007英寸内圈故障驱动端轴承振动退化趋势 (d) 12 kHz、0.007英寸内圈故障扇端轴承振动退化趋势 (e) 12 kHz、0.007英寸内圈故障基座轴承振动退化趋势 (f) 12 kHz、0.014英寸内圈故障基座轴承振动退化趋势 (g) 12 kHz、0.014英寸内圈故障驱动端轴承振动退化趋势 (h) 12 kHz、0.014英寸内圈故障扇端轴承振动退化趋势 (i) 12 kHz、0.007英寸扇端故障基座端轴承振动退化趋势 (j) 12 kHz、0.007英寸扇端故障驱动轴承振动退化趋势

Figure 10. Prediction of gearbox bearing degradation trend of rice bowl seedling transplanter based on TCN

图10. 基于TCN的水稻钵苗移栽机齿轮箱轴承退化趋势预测

根据上图10可知，利用时间卷积网络进行水稻钵苗移栽机齿轮箱轴承退化趋势预测不仅可以挖掘信号内部的隐藏特征，而且在不同尺寸、不同故障类型、不同传感器采集到的振动信号上都有较为明显的改善，因此可以认为基于小波阈值去噪和时间卷积网络的水稻钵苗移栽机齿轮箱轴承退化趋势预测的模型是可行的。

4. 结论

针对机器学习在大规模数据集上运算效率的问题，本文使用了时间卷积神经网络(TCN)构建水稻钵苗移栽机齿轮箱轴承退化趋势预测模型，深度学习模型通过使用隐藏层挖掘非平稳的时间序列中的深层、抽象的特征以解决时间序列中的长期依赖特性。时间卷积网络通过不同尺寸的卷积核对轴承振动信号进行卷积，实现对历史信息的特征提取；其次，通过链式结构实现网络的参数共享，有效解决长时间序列下的低预测精度等问题；最后，时间卷积网络通过引入因果卷积、跳层连接与残差网络等结构，使得其在CNN与RNN的基础上能够有效解决梯度消失或爆炸等问题，捕捉序列的长期退化趋势与轴承振动信号间的非线性关系。