液滴偏心碰撞的多体耗散粒子动力学研究

A Many-Body Dissipative Particle Dynamics Study of Droplets Eccentric Impacting on Fi-ber

摘要: 液滴碰撞细杆的现象在日常生活中随处可见，本文采用了多体耗散粒子动力学(MDPD)模拟液滴以不同角度偏心碰撞圆柱形杆，研究了不同碰撞速度，不同碰撞角度以及不同偏心率对于液滴薄片比例和临界速度的影响。结果表明，分裂滴落的临界速度随着偏心率增大先减小而后增大，不同角度下，临界速度的改变趋势类似，接触细杆的临界速度随着偏心率增大而减小。

Abstract: The phenomenon of droplet impacting on the fiber can be seen everywhere in our daily life. In this paper, we use Many-body Dissipative Particle Dynamics (MDPD) to simulate the droplet eccentric collision with a fiber at different angles. The results show that the critical velocity of splitting drop-ping decreases first and then increases with the increase of eccentricity. The changing trend of crit-ical velocity is similar at different angles, and the critical velocity of contacting fiber decreases with the increase of eccentricity.

1. 引言

液滴碰撞圆柱体表面在自然界和日常生活中是很常见的现象，输电线路在寒冷天气情况中的结冰问题便是其中的一种，一直困扰着许多国家和地区，而防结冰是受关注的有效方法之一。液滴碰撞固体的实验一直被用于探究表面特性和液滴动力学，通过研究液滴碰撞圆柱体表面的铺展特征，对于输电线路防除冰的问题能够提供有效的应对方法和思路。

已经有许多文章关于液滴碰撞固体进行了许多的实验和数值研究。在实验上，Banitabaei [1] 研究了液滴碰撞球形固体，发现在疏水性表面上，液滴扩散时会形成锥形薄片，随着韦伯数的增加，薄片拉伸长度和锥角会相应增加。Zhang [2] 发现研究了对液滴施加不同碰撞速度撞击不同直径比的超疏水圆柱体表面所产生的影响。Khurana [3] 研究了液滴撞击不同直径的亲水和超疏水圆柱表面上后的形态和动力学，提出了用于预测给定圆柱体表面上的润湿系数的理论模型。Liu [4] 研究了液滴碰撞亲水、疏水和超疏水圆柱形表面，发现圆柱体直径越小，液滴越容易发生破碎，反之会促进液滴的回缩和反弹。在仿真模拟方面，Wang [5] 通过MDPD方法，探究液滴碰撞圆柱体的冲击动力学特性，发现液滴碰撞疏水表面更容易引起接触线的回缩。Wang [6] 等人使用MDPD方法模拟了液滴碰撞不同倾斜角度的细杆，首先他们通过与实验比较来验证方法的可行性，然后研究了液滴偏心率、杆的倾斜角和润湿性对碰撞结果的影响，发现液滴临界速度、润湿长度、接触时间和液滴捕获率均随细杆倾角的增大而增大，随偏心距增大而减小。此外，他们还发现细杆的表面润湿性对接触时间的影响不大，但对临界速度的影响较大。

液滴在圆柱体上的碰撞已经开展了广泛的研究，但大多数研究都集中于液滴以中心位置碰撞，对于液滴以一定角度的偏心碰撞涉及较少。在本文中，通过多体耗散粒子动力学的方法对液滴偏心碰撞细杆进行了模拟，系统了解碰撞角度和偏心率对于碰撞结果的影响。

2. 方法和模型设置

2.1. 多体耗散粒子动力学方法

本文使用多体耗散粒子动力学 [7] [8] [9] [10] 的方法进行仿真，是基于经典的耗散粒子动力学(DPD)改进而来的一种无网格数值方法，弥补了DPD方法不能解决液体和气体共存系统问题的不足。通过粒子间的相互作用来模拟系统，相互作用力 $F_{ij}$ 为三种不同力的总和，分别为保守力 $F_{ij}^C$ 、耗散力 $F_{ij}^D$ 和随机力 $F_{ij}^R$ ，方程如下：

$F_{ij}^C=A{\omega }^C\left(r_{ij}\right)e_{ij}+B\left({\bar{\rho }}_i+{\bar{\rho }}_j\right){\omega }_d\left(r_{ij}\right)e_{ij}$ (1)

$F_{ij}^D=-\gamma {\omega }^D\left(r_{ij}\right)\left(e_{ij}\cdot v_{ij}\right)e_{ij}$ (2)

$F_{ij}^R=\sigma {\omega }^R\left(r_{ij}\right){\xi }_{ij}{e}_{ij}$ (3)

公式1中A和B分别为吸引力系数和排斥力系数，

${\omega }^C\left(r_{ij}\right)=1--\frac{r_{ij}}{r_c}$ (4)

${\omega }_d\left(r_{ij}\right)=1-\frac{r_{ij}}{r_d}$ (5)

是具有不同截止半径的权函数， $r_{ij}$ 为粒子i和粒子j的之间的直线距离， $e_{ij}$ 为两个粒子之间的相对位置方向，密度权函数 ${\omega }_{\rho }\left(r_{ij}\right)$ 为 ${\bar{\rho }}_i$ 和 ${\bar{\rho }}_j$ 的总和，其公式为：

${\omega }_{\rho }\left(r_{ij}\right)=\frac{15}{2\text{π}{r}_d^3}{\left(1-\frac{r_{ij}}{r_d}\right)}^2$ (6)

公式2中 $\gamma$ 为耗散力系数，负号代表力的方向与粒子相对运动方向相反， ${\omega }^D\left(r_{ij}\right)$ 也是关于 $r_{ij}$ 的权函数， $v_{ij}=v_i-v_j$ ，为粒子之间的相对速度。公式3中 $\sigma$ 为正的随机力系数， ${\omega }^R\left(r_{ij}\right)$ 与 ${\omega }^C\left(r_{ij}\right)$ 、 ${\omega }^D\left(r_{ij}\right)$ 相同也是关于粒子相对距离的权函数。 ${\xi }_{ij}$ 为随机变量，代表两粒子间产生的随机扰动。 $\sigma$ 和 $\gamma$ 满足关系式 ${\sigma }^2=2\gamma k_{B}T$ ，其中 $k_B$ 为Boltzmann常数，T为系统的温度，这种关系耦合了耗散力和随机力。本文采用开源仿真软件LAMMPS实现，仿真流程图如图1所示。

Figure 1. Simulation flowchat

图1. 仿真流程图

2.2. 模型建立

碰撞模型如图2所示，其中 $e^{\text{*}}=\frac{2\text{*}e}{D_0+D}$ ，偏心长度e顺时针方向偏移为正，逆时针方向偏移为负， $\theta$

为液滴中心与细杆中心的角度，仿真中液滴粒子相关参数的设置在表1中列出。

Table 1. Droplet particle related parameters

表1. 液滴粒子相关参数

Figure 2. System model diagram

图2. 系统模型示意图

3. 结果与分析

液滴以一定角度碰撞细杆时，由于施加的碰撞速度和重力的方向不一致，会导致碰撞状态有所不同。图3展示了液滴以不同角度碰撞细杆的形态变化，左侧为时刻 $t/T$ ，t表示当前时刻，t为整个碰撞过程的时间，施加的碰撞速度 $V=5.7\left(\text{m/s}\right)$ ，此时液滴中心碰撞细杆会分裂为两团小液滴滴落，方便直观地看出液滴的形态变化。由图可知，液滴在碰撞过程的形态变化与中心碰撞相类似；与中心碰撞最直观的区别是，在拉伸断裂之前，两段薄片的扩散方向有所不同，两段薄片所包含的液滴体积相近似，且不会随着碰撞角度的增大而变化； $t/T=0.84$ 时，当液滴以角度θ = 30˚、60˚碰撞细杆，两团小液滴在扩散的过程中汇聚成了一团液滴，可见最终状态会受到碰撞角度的影响。

图4显示了不同时刻，液滴以θ = 0˚、60˚碰撞细杆的速度矢量分布图，以此了解影响碰撞状态的原因，右侧热力图通过速度 $v_{mag}$ 与初始碰撞速度V的比值进行归一化。当液滴以θ = 0˚碰撞细杆，即中心碰撞时，两段薄片外部的速度较大，而靠近细杆的部分速度较小，此外左右两段薄片的速度分布也较为对称，图中 $t/T=0.4$ ，此时与细杆完全接触的液滴，受到细杆表面向上力的影响，液滴速度降低，而靠近细杆的两薄片则出现了向内收缩的趋势；接着在 $t/T=0.7$ 两段薄片继续向内收缩，从而液滴汇聚。当液滴以θ = 60˚碰撞细杆时，液滴整体的速度分布仍是靠近细杆的较小而远离细杆的较大，但此时液滴的速度分布不再对称，当 $t/T=0.4$ ，一段薄片由于受到重力的影响，速度略大于另一段，由速度矢量图可以看出，左右两段薄片的速度不再是镜像对称的关系，速度较大的部分向下滴落的趋势也较明显；当 $t/T=0.7$ ，偏移一侧的薄片向下的移动更明显，而另一段薄片仍以斜向下的方向扩散，接着两段薄片汇聚形成一团液滴。由此可以看出不同角度碰撞改变了分裂的两段薄片扩散方向，而导致了结果的不同。

Figure 3. Morphological Changes of dropletat θ = 0˚, 30˚ and 60˚

图3. 液滴以θ = 0˚，30˚和60˚碰撞细杆的形态变化

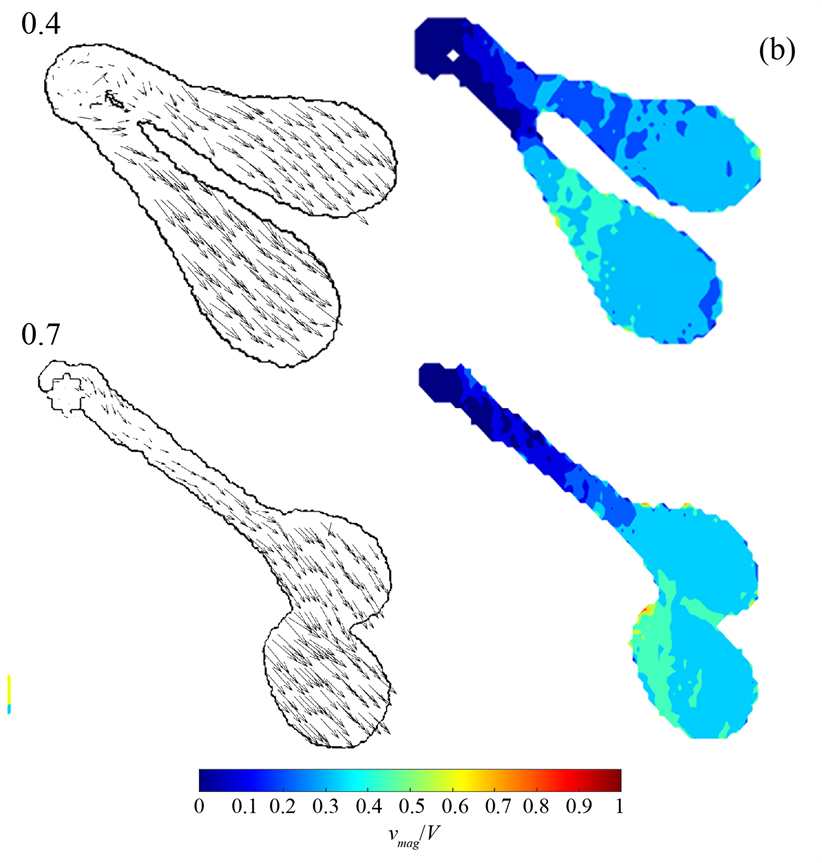
Figure 4. Velocity vector distribution when droplet impact on fiber with (a) θ = 0˚, (b) θ = 60˚ at V = 5.7 (m/s)

图4. V = 5.7 (m/s)时，液滴以(a) θ = 0˚，(b) θ = 60˚碰撞细杆时的速度矢量分布

液滴以不同角度碰撞的分裂滴落临界速度 $V_{as}$ ，如图5所示，进行了多次模拟，得到了不同角度下液滴分裂滴落临界速度的最大和最小误差。由图可以看出碰撞角度与临界速度的变化的规律如下：θ = 10˚至θ = 40˚，随着角度的增加，临界速度随之增大，在θ = 45˚左右时，临界速度较大，表明此时扩散阶段的两段薄片比较容易在分裂后形成一团液滴；之后临界速度随θ的增大而减小。

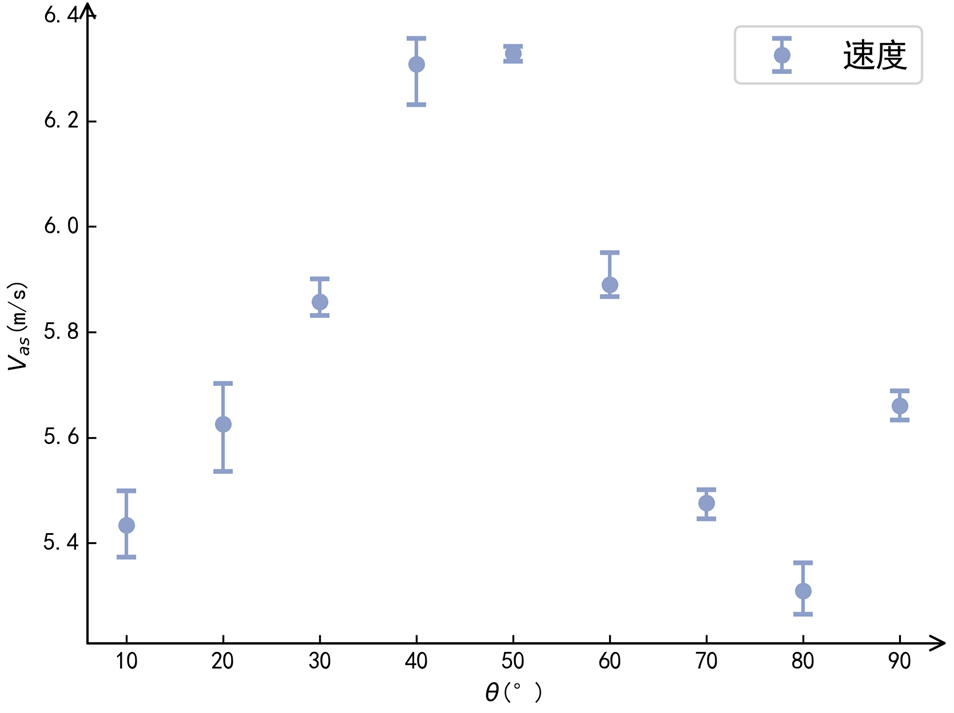
Figure 5. Critical velocity of droplet splitting atdifferent angles

图5. 不同角度碰撞下液滴分裂滴落的临界速度

碰撞的最终状态可分为：未接触，回弹，浸润滴落和分裂滴落，由于受到重力影响，当碰撞角度θ大于50˚时，若碰撞速度较小，液滴会垂直向下移动，此时则会出现液滴没有与细杆接触的情况，图6汇总了不同碰撞速度和碰撞角度下液滴的最终状态，图中的线段是根据拟合得出的不同状态的临界曲线，其中：粉色曲线为未接触与液滴回弹状态的临界曲线，蓝色曲线为回弹和浸润滴落状态的临界曲线，绿色曲线为浸润滴落和分裂滴落状态的临界曲线，碰撞结果的变化规律可以归结为以下几种情况：当V和θ都较小时，液滴在接触细杆后慢慢回弹并离开细杆表面；随着V和θ增大，液滴接触并完全浸润细杆表面后滴落；继续增大V，液滴接触细杆后沿着接触线的方向继续向外扩散，分裂成两团次级液滴并滴落，当碰撞速度V = 6 (m/s)时，θ = 40˚至50˚的碰撞结果为浸润滴落，结合图5可知当θ位于45˚左右时，液滴需要较大的碰撞速度才能分裂滴落。

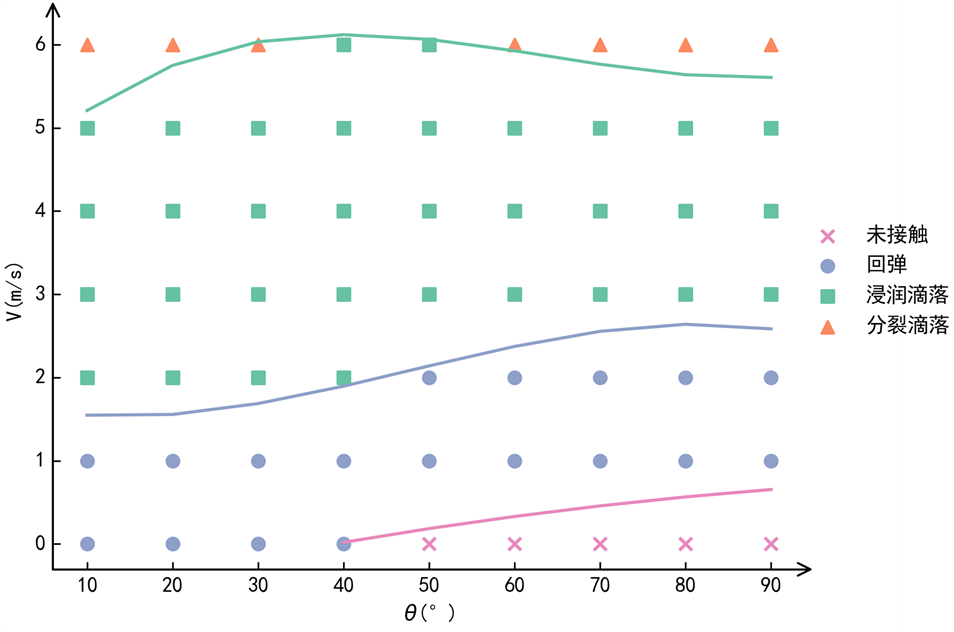
Figure 6. The state of droplet at different angles and velocities

图6. 不同碰撞角度和速度时，液滴的最终状态

图7显示了液滴以不同角度偏心碰撞细杆的形态变化。随着偏心率e^*的增大，两侧的薄片所含液滴比例不同，因此在随后的扩散阶段不呈对称的关系；当偏心率e^*较大时，在浸润阶段(如图中θ = 0˚，e^* = 0.7)，大部分液滴都聚集在偏移一侧，另一侧的液滴较少，所以在随后的扩散阶段不会形成薄片；比较图中θ = 30˚，e^* = 0.3与θ = 60˚，e^* = 0.5可以看出液滴与细杆接触阶段( $t/T=0.4$ )，两者形态类似，在随后的扩散阶段不同角度的偏心碰撞会引起两段薄片的形态有所不同。

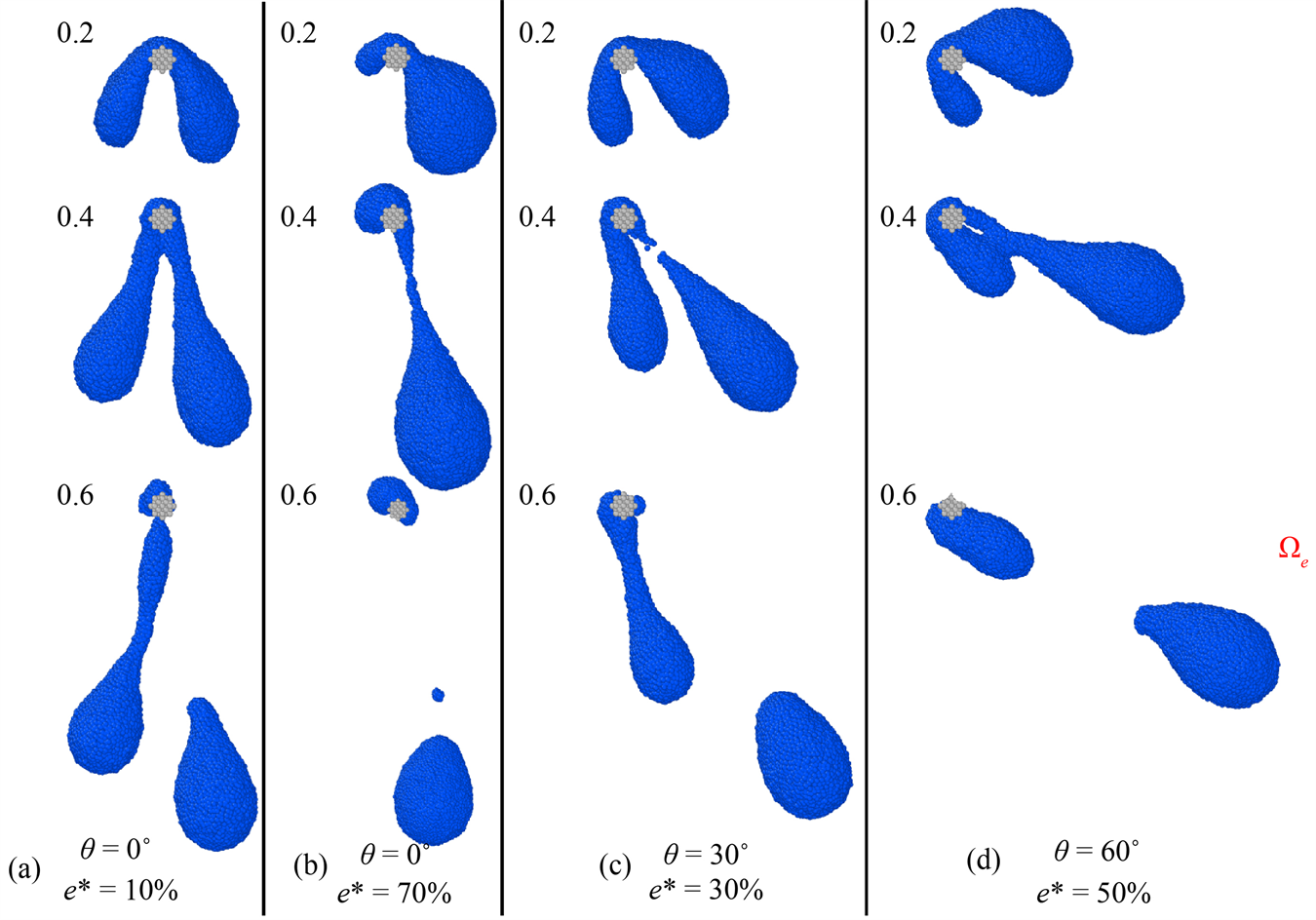
Figure 7. Morphological changes of droplet eccentrically impacting on fiber at different angles

图7. 液滴以不同角度偏心碰撞细杆的形态变化

不同碰撞角度和偏心率左右两段薄片液滴比值定义为 $\text{Ω}=\left({\text{Ω}}_0-{\text{Ω}}_e\right)/{\text{Ω}}_e$ ，其中 ${\text{Ω}}_0$ 为液滴初始所含颗粒数， ${\text{Ω}}_e$ 为偏移一侧薄片所含颗粒数。图8显示了在扩散阶段，图中的虚线表示e^* = 10%和e^* = 50%时，所对应的 值，通过与e^*为负值时对比，随着e^*的增大，液滴比值Ω随之递减，大致上呈现如图中二次曲线的规律变化，变化如图中黑色曲线；此外当e^*较小时，碰撞角度对Ω的影响也较明显，随着e^*增加，不同碰撞角度下的Ω之间的差值减小。逆时针偏移时即e^*为负值，Ω比顺时针偏移时较小，因为此时一侧薄片受到重力的影响更明显，在接触细杆之前偏移一侧包含更多液滴，进而导致在扩散阶段两段薄片更加不对称。

与中心碰撞不同，由于偏移一侧薄片所含液滴较多，牵引另一侧的薄片，因此当偏心率较大时、速度较小时如V = 4.2 (m/s)，两侧的薄片有短暂的汇聚，但两者的移动方向不同导致最终在随后的拉伸断裂阶段形成两团小液滴，如图9(a)所示的速度矢量分布和热力图。当偏心率更大时，如图9(b)所示，此时Ω更小，即偏移另一侧所含液滴更少，液滴接触杆后，液滴掠过细杆表面，不会形成拉伸的两段薄片，仍然以初始的液滴状态向着斜下方移动。当碰撞角度更大且e^*为负值时，若继续减小碰撞速度V，则会出现液滴没有与细杆接触的情况。

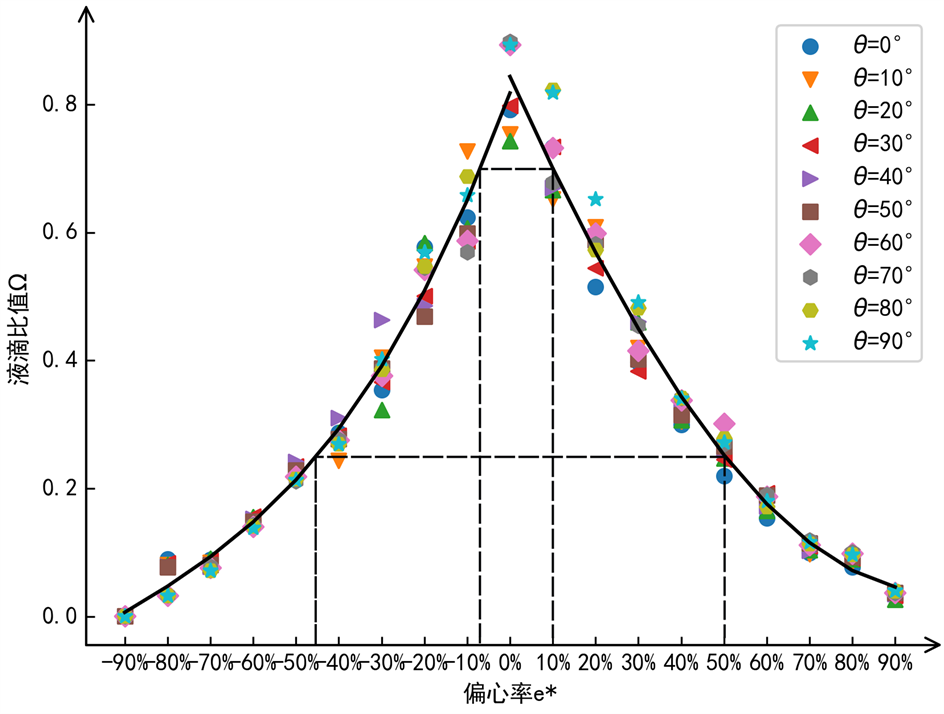
Figure 8. Droplet ratio of two lamellae under different impacting angles and eccentricity

图8. 不同碰撞角度和偏心率下两段薄片所含液滴比例

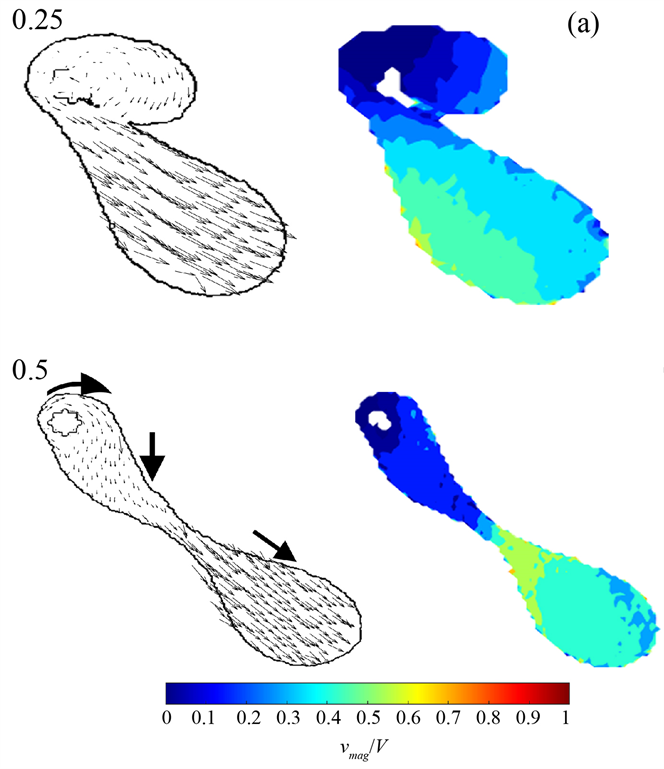
Figure 9. Velocity vector distribution when droplet impact on fiber with (a) e* = −30%, (b) e* = 80% at V = 4.2 (m/s), θ = 60˚

图9. V = 4.2 (m/s)，θ = 60˚时，液滴以(a) e* = −30%，(b) e* = 80%碰撞细杆的速度矢量分布

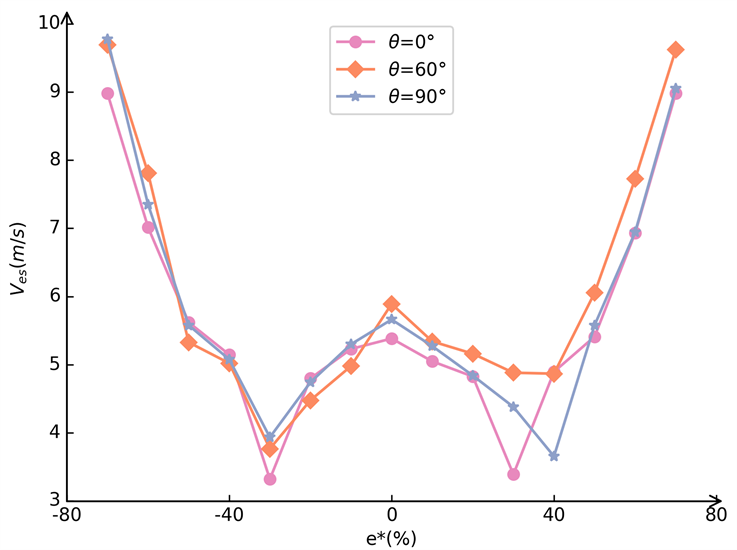
图10显示了不同偏心率和碰撞角度下，液滴与细杆接触的临界速度 $V_{ec}$ 和分裂滴落的临界速度 $V_{es}$ 。如图10(a)所示，当 $e^{\text{*}}>30\%$ (或 $e^{\text{*}}<-30\%$ )时，随着偏移量的增加， $V_{es}$ 随之减小；当偏移量继续增加， $V_{es}$ 随之递增；当 $e^{\text{*}}>70\%$ (或 $e^{\text{*}}<-70\%$ )，偏移一侧所含的液滴较少，因此在扩散阶段不会形成薄片，可见一定的e^*范围之间，能促进液滴分裂滴落。此外，对比θ = 0˚、60˚和90˚，临界速度 $V_{es}$ 的变化规律类似，当e^*相同时 $V_{es}$ 之间的差值较为接近，因此不同的角度对于 $V_{es}$ 的影响较小。当θ ≥ 50˚时，才会出现液滴与细杆没有接触的情况，如图10(b)所示，随着e^*的增加， $V_{ec}$ 递减；同时，当碰撞角度θ增加 $V_{ec}$ 也随之增大。

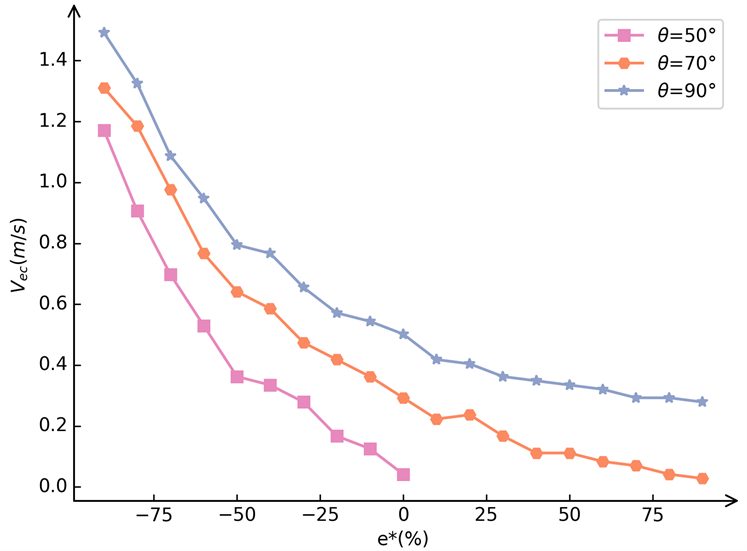(a) (b)

Figure 10. Critical velocity V_es of droplet splitting and critical velocity V_ec of droplet contact with fiber at different eccentricity and angles

图10. 不同偏心率和碰撞角度下，液滴分裂滴落的临界速度V_es (e^* = −70%~70%)和接触细杆的临界速度V_ec

4. 总结

本文采用MDPD方法模拟了液滴以一定角度偏心碰撞圆柱形细杆，单独考虑了碰撞角度对于结果影响，在重力的影响下，液滴以抛物线的轨迹向下移动，扩散阶段中分裂的两段薄片运动方向不同，造成最终的状态发生改变。在一定角度范围内，需要更大的初始速度，液滴才能分裂滴落；此外，当碰撞角度较大时，若碰撞速度较小，液滴不会接触细杆；接着综合考虑了碰撞角度和偏心率对于液滴两侧薄片比例、液滴分裂滴落临界 $V_{es}$ 和接触细杆临界速度 $V_{ec}$ 的影响。结果表明，分裂滴落时的两段薄片所含液滴会随着偏心率改变，而碰撞角度的影响则较小；分裂滴落的临界速度随着偏心率增大先减小而后增大，不同角度下，临界速度的改变趋势类似，接触细杆的临界速度随着偏心率增大而减小。