一种集成电路全局布局混合整数规划模型

A Mixed Integer Programming Model for Global Placement of Integrated Circuit

摘要: 本文提出了一种基于混合整数规划的集成电路全局布局模型，全局布局问题是将一些电子元件摆放在电路板指定的区域，使得元件之间没有重叠同时紧凑的排列。与已有的解析布局算法对比，本文用优化模型精确刻画了半周长线长(Half Perimeter Wire Length, HPWL)目标和无重叠(non-overlap)约束可以得到更精确的布局结果，避免了光滑近似的非精确解。数值实验表明，在中等规模的数据集上，本文的模型可以完全满足无重叠约束的同时，半周长线长也是较小的，得到的高质量解可以作为非精确算法的参考解。本文提出的模型在中小规模的布局问题上有较好的效果，可以用在车载芯片或蓝牙芯片设计等实际问题中，具有良好的应用前景。

Abstract: This paper proposes a mixed-integer programming model for global placement of integrated circuit. The global placement problem can be defined as placing electronic components in a designated circuit board, with no overlap and compact arrangement between these components. Compared with existing analytical placement solvers, the model we presented can accurately characterize the Half Perimeter Wire Length (HPWL) objective and the non-overlap constraint, which can obtain more accurate placement results and avoid non-precise solutions based on smooth approximations. Numerical experiments demonstrate that on medium-sized datasets, the proposed model can fully satisfy the non-overlap constraint while achieving a relatively small HPWL, and the obtained high quality solution can serve as a reference for non-precise algorithms. The proposed model performs well on small to medium-sized placement problems and can be applied to practical design problems such as vehicle-mounted chips or Bluetooth chips, with good application prospects.

1. 引言

数字经济日益成为国民经济发展重要的方向，对人们的生产生活都有很多有益的影响。计算机作为数字经济的基础设施在其中起到了重要的作用，支撑计算机高效运行的关键部件是各种电子元件，例如CPU，存储器，控制器等。这些电子元件都是由各种类型的晶体管构成，计算机的运行效率取决于这些电子元件的计算能力，尤其是取决于CPU即通常所说的芯片的计算能力。通常我们将这些电子元件看作是一种集成电路(integrated circuit)，由于国外对我国的技术封锁，如何自主制造这些精密的电子元件是一个亟待解决的问题。

集成电路设计和制造是一个复杂且漫长的过程，大致包括系统设计，逻辑设计，物理设计，参数检验，功能验证，封装等步骤 [1] 。本文研究的焦点在于设计流程中的物理设计，物理设计主要作用是在指定的区域中摆放晶体管即物理单元，使得电子元件的性能高的同时，功耗和电路面积尽可能的少。物理设计的主要流程有布图规划，布局，布线和版图规划。布图规划是确定布图区域的大小，I/O模块，规定宏物理单元的位置，设计电源线。布局是摆放标准物理单元到合法的位置，插入填充单元，进行时序优化，无重叠优化使得设计目标最优。布线主要是设计时钟网络，实现时钟同步，功耗低等目标。版图规划是将布线过程的连线进行通道化(track)和实体化，使得线长短，时序功耗低，设计规则满足。对于布局流程，又可以分为全局布局(global placement)，合法化(legalization)，详细布局(detailed placement)三个部分 [1] 。全局布局的作用是确定宏单元和其他物理单元的位置，优化目标有线长，功耗，可制造性等，约束主要是密度约束。合法化主要是将单元放置在电路板中特定的行中，确定火线和零线的方向，保证单元的电路功能正确。详细布局是通过行单元的交换，插入，单元反转等，将前序工序的布局结果进一步优化，比如去除单元之间的重叠。在设计结束后，需要将设计图提交工厂进行制造，制造过程主要是光刻机在电路板上进行蚀刻光照等复杂物理过程，最终生产出可用的芯片。

本文主要关注集成电路设计中的物理设计，从中选取布局流程的全局布局步骤作为研究对象。建立了一个混合整数规划模型。用数学模型精确的刻画半周长线长(HPWL)和无重叠约束(non-overlap) [2] ，这两个指标的优化会对集成电路的性能有深刻的影响，更小的线长代表着更满足时序要求且高可制造性，无重叠则表示芯片的功耗低从而提升芯片的计算性能，通过求解混合整数规划模型对实际的集成电路布局问题进行求解，以达到设计出更好的芯片的目的。

2. 背景

本文以CPU即通常指代的芯片为例，说明一下集成电路全局布局的问题和背景，现有的研究成果。芯片又称为中央处理器。是计算机进行科学计算的主要部件，现代计算机使用的芯片有大约数十亿个晶体管即物理单元组成以实现复杂和高效的计算，芯片的面积在100 mm²左右，功耗在数百瓦。通常来讲，评价芯片性能优劣的指标有性能(performance)，功耗(power)，面积(area) [2] ，好的芯片特征是拥有更好的性能，更低的功耗和尽可能小的面积，业界将这三个关键指标称为PPA设计目标。

为了达到更佳的PPA指标，需要对芯片中的部件在电路板上进行精密的排列与连接。其中物理单元的排列称为布局(placement)，布局通过对单元的排列得到尽可能紧凑且较少重叠的布局结果。用数学语言表述为，通过极小化半周长线长(Half Perimeter Wire Length, HPWL)表征紧凑的排列，通过计算物理单元之间的坐标代数关系，表征晶体管之间无重叠(non-overlap) [2] 。

电路板中的布局问题描述为，给定版图规格后，设计者需要根据晶体管的尺寸大小和晶体管的之间的连接，将晶体管在版图规定的区域内恰当放置，一般而言，晶体管为矩形形状。满足晶体管之间无重叠，最优化线长，时序，功耗等性能，芯片制造商会提供晶体管尺寸文件(nodes file)，晶体管连接情况(netsfile即线网文件)以让设计者根据这些信息进行布局问题的求解。

已有理论证明，布局问题是NP-难问题。国内外有许多关于布局问题的求解算法，例如有二次规划，模拟退火等智能算法，超图划分等方法求解布局问题 [1] 。近年来解决布局问题的主要方法是基于解析模型的布局算法和基于强化学习的布局算法。

2.1. 基于解析模型的布局算法

以NTUplace3 [3] ，ePlace [4] 和DREAMPlace [5] 为代表布局求解器都是解析模型来求解布局问题，这类布局求解器考虑一个光滑化的半周长线长函数，并且建立一个密度函数来近似表示无重叠约束。对于线长的处理，这三种算法采用了一些数学方法对半周长线长做光滑近似，NTUplace3引入bin (一种特殊的矩形区域)近似无重叠约束，ePlace引入物理学中的静电场概念，将无重叠约束用偏微分方程近似。DREAMPlace借助了ePlace的静电场思想，将布局问题转化为一个机器学习中求损失函数极小值的问题，通过Pytorch这类深度学习框架高效求解布局问题并采用光滑化的方法，可以使用罚函数法和共轭梯度法求解布局问题。同时，为了求解更大规模的问题，这些解析方法会使用多级聚类解聚类框架 [11] 以减少晶体管的数量规模。近两三年，学者在光滑模型的基础上，考虑时序裕量 [6] 和雾化效应 [7] 等约束，进一步扩展模型的使用范围。

从实际应用来看，光滑化的模型广泛的使用在布局求解器中。但光滑化模型的不足是，对于只含有2个或3个引脚的布局问题，光滑化模型会低估实际的半周长线长，并且求到的解不能完全去除物理单元之间的重叠。虽然在后续流程可以处理重叠约束，若可以将关口前移，在全局布局阶段处理好无重叠约束，对后续的流程会有一定的增益。目前工业界中也广泛使用解析模型的布局算法或布局求解器，国内厂商以上海立芯布局求解器LePlace和华大九天PowerPCB等为代表，可以实现7 nm制程的芯片设计布局求解。这些工业界使用的布局求解器以解析模型为主，在全局布局阶段得到一个重叠度较低的初始布局结果和半周长线长的下界，之后通过合法化和详细布局调整单元最终得到合适的布局。

2.2. 基于强化学习的布局算法

2021年，Mirhoseni等人在Nature上提出用强化学习的方法 [8] 求解芯片设计中的布局问题，文章收集了大量的已布局好的芯片文件作为训练数据集，训练一个强化智能学习体，对布局结果进行编码学习从而得到一个好的布局智能体。随后再向智能体输入测试文件，智能体首先对确定一部分单元例如I/O模块的位置，随后使用其他布局算法例如Force-Direct确定其余物理单元的位置，获得最终的布局结果。

强化学习方法的主要优势在于，该方法本质上求解的是一个多目标优化问题，得到的解不仅在无重叠约束上有改进，在其他的指标例如时序裕量也有所改进。相比于解析方法，模型覆盖的情形更加全面，得到的解会更接近工业界的实际需要。文章中指出，该方法在6个小时内可以得到芯片布局结果，其求解质量可以和人类专家相当，即将用在Google下一代张量处理器(Tensor Processing Unit, TPU)的设计中。但同时文章也提到，这种方法需要大量的芯片布局数据进行训练，需要巨大的算力和训练数据支撑，模型训练代价高昂且智能体对于不同类型芯片的泛化能力仍有不确定因素。

3. 一种布局问题的混合整数规划模型

3.1. 模型提出

本文使用混合整数规划模型刻画芯片设计中的全局布局问题，基本思路是用绝对值函数来表达半周长线长，并通过引入一些0-1变量精确表达单元之间无重叠的约束。该模型是对全局布局问题的精确描述，因此相比光滑化的近似模型可以得到更精确的解，在数学上也具有更好的可解释性。同时可以为非精确的算法提供一组参考解。

3.2. 模型建立

3.2.1. 符号说明

芯片或者集成电路全局布局问题可以用超图来建模，记 $H\left(V,E\right)$ 表示一个布局问题，记布局区域的物理单元指标集合 $I=\left\{1,2,\cdots ,n\right\}$ 。其中 $V=\left\{v_i|i\in I\right\}$ 表示物理单元的集合(下称此集合为cells，集合中的每个元素称为单元)， $E=\left\{e_i|i\in I\right\}$ 是线网(nets)的集合，这里的线网记录了单元之间的连接，可以看作超图的一条超边。记布局区域的宽和高分别为W和H，记集合 $W=\left\{w_i|i\in I\right\}$ 和 $H=\left\{h_i|i\in I\right\}$ 分别是集合cells元素中的宽和高。记 $V_X=\left\{x_i|i\in I\right\}$ 和 $V_Y=\left\{y_i|i\in I\right\}$ 是各个单元的中心点坐标。

布局问题的数学模型可以用模型(1)表达，其中的约束就是对无重叠情形的精确描述，即单元之间在横坐标上或纵坐标没有重叠，数学上表示为两个单元的横坐标或纵坐标之差的绝对值大于两个单元宽或高之和的一半。

$\begin{array}{l}\min HPWL\left(x,y\right):={\displaystyle \underset{e\in E}{\sum }\underset{v_i,v_j\in e}{\max }}\left\{\left|x_i-x_j\right|+\left|y_i-y_j\right|\right\}\\ s.t.\left|x_i-x_j\right|\ge w_{ij}\text{or}\left|y_i-y_j\right|\ge h_{ij},i\ne j\in I\\ \left(x,y\right)\in X\times Y\end{array}$ (1)

其中， $w_{ij}=\frac{w_i+w_j}{2},h_{ij}=\frac{h_i+h_j}{2}$ ， $X,Y$ 是布局边界约束。

$\begin{array}{l}X:=\left\{x\in R^n|\frac{w{}_i}{2}\le x_i\le W-\frac{w_i}{2},i\in I\right\}\\ Y:=\left\{y\in R^n|\frac{h_i}{2}\le y_i\le H-\frac{h_i}{2},i\in I\right\}\end{array}$

3.2.2. 优化目标

从模型(1)出发，为了去掉目标函数的绝对值运算，引入两个连续变量 ${\alpha }_e,{\beta }_e$ 将目标函数重写，并且为了和(1)等价，需要在约束中加入两条额外的约束表示极小化目标的含义。

$\begin{array}{l}\min {\displaystyle \underset{e\in E}{\sum }\left({\alpha }_e+{\beta }_e\right)}\\ s.t.-{\alpha }_{\text{e}}\le x_i-x_j\le {\alpha }_e,\forall \left(i,j\right)\in e,\forall e\in E\\ -{\beta }_{\text{e}}\le y_i-y_j\le {\beta }_e,\forall \left(i,j\right)\in e,\forall e\in E\\ \left|x_i-x_j\right|\ge w_{ij}\text{or}\left|y_i-y_j\right|\ge h_{ij},i\ne j\in I\\ \left(x,y\right)\in X\times Y\end{array}$ (2)

以第一条约束为例， $x_i-x_j$ 被 ${\alpha }_e$ 和 $-{\alpha }_e$ 控制，因此当 ${\alpha }_e$ 取最小值时，也就意味着 $\left|x_i-x_j\right|$ 取到了最小值，第二条约束同理可得。

3.2.3. 问题约束

同样从模型(1)出发，为了去掉约束中的绝对值符号和两个约束的逻辑or运算，可以使用大M法并引入一些0-1变量处理。首先对无重叠约束进行如下处理，

$\frac{\left|x_i-x_j\right|}{w_{ij}}:=\left|X_{ij}\right|\ge 1\text{or}\frac{\left|y_i-y_j\right|}{h_{ij}}:=\left|Y_{ij}\right|\ge 1$ (3)

引入两个0-1变量 $p_{ij},q_{ij}\in \left\{0,1\right\}$ ，使得上面带有逻辑算子or的约束有一个成立，具体表达式如下。

$\begin{array}{l}-\left(M_{ij}+1\right)\left(p_{ij}+q_{ij}\right)+1\le X_{ij}\le -\left(M_{ij}+1\right)\left(p_{ij}+q_{ij}\right)+2M_{ij}+1\\ -\left(N_{ij}+1\right)\left(q_{ij}-p_{ij}\right)-N_{ij}\le Y_{ij}\le -\left(N_{ij}+1\right)\left(q_{ij}-p_{ij}\right)+N_{ij}\end{array}$ (4)

下面对 $p_{ij},q_{ij}$ 的值列举来证明(3)和(4)在表达上是等价的。

$\begin{array}{l}\left(p_{ij},q_{ij}\right)=\left(0,0\right)\to 1\le X_{ij}\le 2M_{ij}+1,-\text{}{N}_{ij}\le Y_{ij}\le N_{ij}\\ \left(p_{ij},q_{ij}\right)=\left(0,1\right)\to -M_{ij}\le X_{ij}\le M_{ij},-2N_{ij}-1\le Y_{ij}\le -1\\ \left(p_{ij},q_{ij}\right)=\left(1,0\right)\to -{\text{M}}_{ij}\le X_{ij}\le M_{ij},1\le Y_{ij}\le 2N_{ij}+1\\ (p_{ij},q_{ij})=\left(1,1\right)\to -2M_{ij}-1\le X_{ij}\le -1,-N_{ij}\le Y_{ij}\le N_{ij}\end{array}$ (5)

以第一个约束为例，当 $\left(p_{ij},q_{ij}\right)=\left(0,0\right)$ 时， $\left|X_{ij}\right|\ge 1$ 成立，通过观察其他三个表达式，可以看到 $\left(p_{ij},q_{ij}\right)$ 的取值覆盖了所有可能的情形，并且与(3)的约束等价。

3.2.4. 数学模型

综上所述可以建立如下的混合整数规划模型。

$\begin{array}{l}\min W\left(x,y\right)={\displaystyle \underset{e\in E}{\sum }\left({\alpha }_e+{\beta }_e\right)}\\ s.t.-{\alpha }_e\le x_i-x_j\le {\alpha }_e,\forall \left(i,j\right)\in e,\forall e\in E\\ -{\beta }_e\le y_i-y_j\le {\beta }_e,\forall \left(i,j\right)\in e,\forall e\in E\\ -\left(M_{ij}+1\right)\left(p_{ij}+q_{ij}\right)+1\le \frac{x_i-x_j}{w_{ijj}}\le -\left(M_{ij}+1\right)\left(p_{ij}+q_{ij}\right)+2M_{ij}+1,\forall i\in V,\forall j\in V\\ -\left(N_{ij}+1\right)\left(q_{ij}-p_{ij}\right)-N_{ij}\le \frac{y_i-y_j}{h_{ij}}\le -\left(N_{ij}+1\right)\left(q_{ij}-p_{ij}\right)+N_{ij},\forall i\in \text{V},\forall j\in V\\ p_{ij},q_{ij}\in \left\{0,1\right\}\end{array}$ (6)

考虑到实际问题中 $M_{ij},N_{ij}$ 的有界性，可以取恰当的充分大的值，例如令 $M_{ij}=W,N_{ij}=H$ 。

4. 数值实验

在数值实验中，我们在Linux操作系统中使用C++编写数值计算程序，并使用CPLEX作为混合整数规划求解器。实验选取的数据集来自密歇根大学维护的GSRC [9] 和MCNC [10] 数据集。我们对比了本文提出的混合整数规划模型和光滑化模型得到效果。实验结果表明，光滑化模型得到的线长虽然较小，但是没有完全去除单元之间的重叠，然而本文的模型在和光滑模型线长相当的情形下，可以做到完全没有重叠，从而得到了一个质量更好的解。

4.1. 数据集说明

GSRC和MCNC数据集是由密歇根大学维护的一个电路板布局数据集。我们以GSRC中的HARD文件夹下的n10算例做说明。首先这个算例包含两个文件n10.blocks和n10.nets。blocks文件存储了单元的信息，其中一些称为宏单元的模块存储了该模块4个位置的坐标，其余的单元我们令其宽为1高为1的正方形，这个文件就是前述的尺寸文件(nodes file)。我们通过编写Python程序进行预处理可以计算出这些宏单元的宽高，生成新的blocks文件。第二个是nets文件，这个文件存储了单元之间的连接。一个net即线网包含了若干个单元，同属于一个net的单元互相之间都有连接，从数学的角度看，每一个net都是超图中的一条超边。这两个数据集分为HRAD和SOFT两部分，HARD部分意味着宏单元大小是不可变的，实验中我们使用HARD部分的数据。

4.2. 数值结果

图1是使用光滑化模型的实验结果，我们选取了n10算例，这个算例包含79个单元(cells)，其中有10个宏单元(blocks)，118个线网(nets)。光滑模型我们参考文献 [3] 的方法，使用罚函数方法和共轭梯度法求解。图1的横轴表示布局区域的横坐标，纵轴表示布局区域的纵坐标。其中数字代表布局区域的大小，并表示了单元的位置坐标。单元的摆放从(0, 0)开始，但为了作图方便，布局结果图左下端的坐标从(−100, −100)开始。从图1中看到，光滑模型得到的半周长线长为19,233，但是图中的单元之间仍有重叠，尤其是宏单元之间重叠度较高。虽然可以在详细布局等后续流程中得到缓解，但是从光滑模型的近似来看，这个布局结果不是一个高质量的解。

图2是使用本文提出的混合整数规划模型，其中横纵坐标的含义与图1相同，数字含义也与图1相同。该模型得到的半周长线长为19703，略高于光滑模型的线长，但是从图中看到各个单元之间完全没有重叠，是一个满足约束条件的同时，单元之间尽可能紧凑排列的高质量解。不过使用CPLEX求解混合整数规划模型的时间要比光滑化模型的时间长，虽然得到了高质量的布局结果，但是求解时间还有待进一步改进。

Figure 1. Smooth model result on n10 benchmark

图1. 光滑化模型求解n10算例

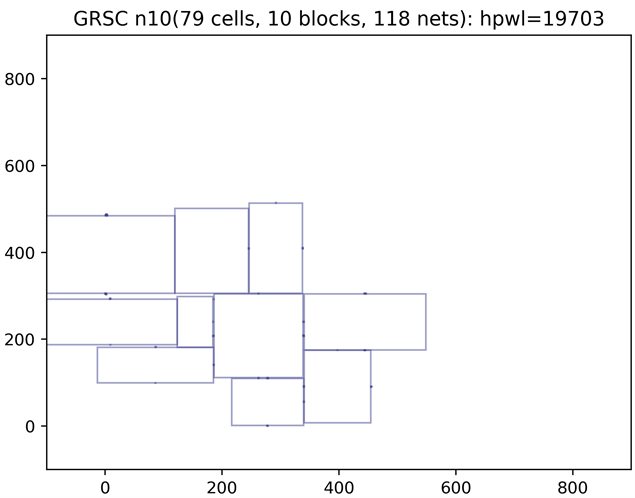
Figure 2. Mixed-integer programming model result on n10 benchmark

图2. 混合整数规划模型求解n10算例

5. 结论

本文提出了一种集成电路全局布局的混合整数规划模型，用优化模型的方法精确刻画了布局问题的关键要素，即半周长线长和无重叠约束。在实际应用中，可以获得高质量的布局结果，相比于已有的解析型布局算法。本文提出的模型可以在全局布局阶段完全满足无重叠约束，对芯片设计的后续流程有增益作用。同时，模型还可以为非精确的算法提供参考解，帮助已有的解析布局器提高求解质量，本文提出的模型还可以与多级聚类解聚类 [11] 等框架结合求解大规模的集成电路布局问题。数值实验表明，本文提出的模型可以得到高质量的解，可以有效求解中小规模的集成电路布局问题。