基于双积分系统轮式倒立摆的鲁棒复合控制

Robust Compound Control for Wheeled Inverted Pendulum Based on Double Integrater System

摘要: 本文研究了轮式倒立摆车轮位置和摆角的复合鲁棒控制方法。所提出的控制算法是时变滑模控制，精度高，抗干扰效果较好，可以消除抖振现象，获得更好的稳定性和跟踪性能。利用拉格朗日和牛顿力学方法推导了倒立摆的非线性动力学模型。利用李雅普诺夫定理证明了该控制方案的收敛性和稳定性。仿真结果表明，所提出的控制方案在消除抖振现象、抑制噪声方面具有良好的性能，可以提高系统的稳定性和缩短响应时间。

Abstract: This paper studies the compound robust control method of wheel position and swing angle of wheel inverted pendulum. The proposed control algorithm is time-varying sliding mode control with high accuracy and good anti-interference effect, which can eliminate chattering and obtain better stability and tracking performance. The nonlinear dynamic model of inverted pendulum is derived by using Lagrange and Newton mechanics methods. The convergence and stability of the control scheme are proved by using Lyapunov theorem. The simulation results show that the proposed control scheme has good performance in eliminating chattering and suppressing noise, and can improve the stability of the system and shorten the response time.

1. 引言

倒立摆系统是一种典型的机械控制系统，用于处理、研究和演示稳定性和控制理论的各个方面。经典倒立摆家族中一个相对较新的成员是轮式倒立摆，它在机器人领域有许多重要的应用，例如独轮车、Segway、JOE和PMP平台 [1] [2] [3] [4] 。这类系统的分析控制设计是一个难题，因为这种系统存在各种内在不确定性、具有高度非线性性、多数为欠驱动系统等。尽管控制这种系统有许多困难，但很多学者已对此进行了研究。

在过去的研究中，对轮式倒立摆的控制主要集中在三个方面，稳定性控制 [5] [6] ，跟踪控制 [7] ，以及摆动控制 [8] [9] [10] 。基于动力学线性化的小扰动理论，已经设计了许多线性控制器来稳定直立不稳定状态下的摆。虽然这样的控制器是可靠的，例如PID控制器，但这种方法的有效范围通常很小，并且这些技术在存在显著的参数不确定性或外部干扰的情况下通常是不够的。

为了克服线性控制器的缺点，一些研究人员提出了若干非线性控制方案。例如，文 [11] [12] 中提出了基于积分反推控制器的WIP自适应控制，以稳定摆角，文 [13] 中利用PD型正反馈控制车轮角度。仿真结果显示了良好的性能，即使出现了相当大的超调，也可达到控制目的。

目前基于滑模面控制(SMC)的方法已成为处理不确定系统的有效方法，因此基于SMC的许多研究已被考虑用于控制倒立摆系统，文 [14] 的作者利用了积分滑模控制(ISMC)来处理移动机器人内在建模不确定性的控制，然而，该算法是基于线性化模型开发的，线性化模型隐含地意味着小的操作区域。文 [15] 中提出了非线性控制策略，包括线性二次调节器(LQR)控制和三种SMC控制方法。仿真结果表明，SMC控制方法在减少抖振方面具有优势。本文对SMC方法进行了改进，提出了基于双积分系统的SMC鲁棒控制技术，在减小抖振的同时具有更快的响应时间。

2. 问题描述

如图1所示，轮式倒立摆可以看作是由小车和均匀的杆组成的系统，其中M代表小车的质量，m代表摆杆的质量，l代表摆杆质心到转动轴心的距离， $\theta$ 代表摆杆与竖直方向的夹角。x代表小车的位置，u代表控制输入。

如图所示，令 $x_1=x,x_2={\stackrel{\dot{}}{x}}_1,x_3=\theta ,x_4=\stackrel{\dot{}}{\theta }$ ，则对小车进行受力分析，有

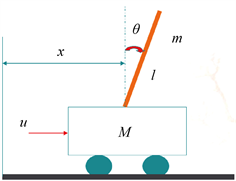
Figure 1. Schematic diagram of the structure of the inverted pendulum trolley

图1. 倒立摆小车结构示意图

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1=x_2\hfill \\ {\stackrel{\dot{}}{x}}_2=u\hfill \\ {\stackrel{\dot{}}{x}}_3=x_4\hfill \\ {\stackrel{\dot{}}{x}}_4=-\frac{3}{4l}g\sin x_3-\frac{3}{4l}g\cos x_3+u\hfill \end{array}$

或可以表示为如下的状态空间形式 $\left(\begin{array}{c}{\stackrel{\dot{}}{x}}_1\\ {\stackrel{\dot{}}{x}}_2\\ {\stackrel{\dot{}}{x}}_3\\ {\stackrel{\dot{}}{x}}_4\end{array}\right)=\left(\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right)+\left(\begin{array}{c}0\\ 0\\ 0\\ -\frac{3}{4l}g\sin x_3\end{array}\right)+\left(\begin{array}{c}0\\ 1\\ 0\\ -\frac{3}{4l}g\cos x_3\end{array}\right)u$

3. 控制律设计

定理系统： $\{\begin{array}{l}{\stackrel{\dot{}}{x}}_3=x_4\hfill \\ {\stackrel{\dot{}}{x}}_4=-\frac{3}{4l}g\sin x_3-\frac{3}{4l}g\cos x_{3}u\hfill \end{array}$

在控制律

$u=\left(-k_{3}sign\left(x_3\right){\left|x_3\right|}^{{\alpha }_1}-k_{4}sign\left(x_4\right){\left|x_4\right|}^{{\alpha }_2}+\frac{3}{4l}g\sin x_3\right)\frac{4l}{3g\cos x_3}$ $k_1>0,k_2>0,0<{\alpha }_1<1,{\alpha }_2=2{\alpha }_1/\left(1+{\alpha }_1\right)$

作用下，可以有限时间镇定。

证明 1) 首先证明系统的渐近稳定性，为此定义Lyapunov函数：

$V\left(x_3,x_4\right)=k_3\frac{{\left|x_3\right|}^{1+{\alpha }_1}}{1+{\alpha }_1}+\frac{1}{2}{\left(x_4\right)}^2$

对 $V\left(x_3,x_4\right)$ 求导，有

$\begin{array}{c}\stackrel{\dot{}}{V}\left(x_3,x_4\right)=k_{3}sign\left(x_3\right){\left|x_3\right|}^{{\alpha }_{{}^1}}{x}_4+x_4\left(-k_{3}sign\left(x_3\right){\left|x_3\right|}^{{\alpha }_1}-k_{4}sign\left(x_4\right){\left|x_4\right|}^{{\alpha }_2}\right)\\ =-k_2{\left|x_4\right|}^{1+{\alpha }_2}\le 0\end{array}$

故有 $V\left(x_3,x_4\right)$ 为非增函数，且有 $0\le V\left(x_3,x_4\right)\le V\left(x_3\left(0\right),x_4\left(0\right)\right)$ 故 $V\left(x_3,x_4\right)$ 应有有限极限， $x_3,x_4$ 均为有界变量，且

$\ddot{V}\left(x_3,x_4\right)=-k_4\left(1+{\alpha }_2\right)sign\left(x_4\right){\left|x_4\right|}^{{\alpha }_2}$

$x_4$ 为有界量，故 $\ddot{V}\left(x_3,x_4\right)$ 有界，由此可知其原函数 $\stackrel{\dot{}}{V}\left(x_3,x_4\right)$ 为一致连续的，故由Barbalat (17)定理知 $\underset{t\to \infty }{\lim }\stackrel{\dot{}}{V}\left(x_3,x_4\right)=0$ 且

$\stackrel{\dot{}}{V}\left(x_3,x_4\right)=-k_4{\left|x_4\right|}^{1+{\alpha }_2}$

知 $\underset{t\to \infty }{\lim }{x}_4=0$ 故由

$\begin{array}{l}{\stackrel{\dot{}}{x}}_3=x_4\\ {\stackrel{\dot{}}{x}}_4=-\frac{3}{4l}g\sin x_3-\frac{3}{4l}g\cos x_3\left(-k_{3}sign\left(x_3\right){\left|x_3\right|}^{{\alpha }_1}-k_{4}sign\left(x_4\right){\left|x_4\right|}^{{\alpha }_2}+\frac{3}{4l}g\sin x_3\right)\frac{4l}{3g\cos x_3}\end{array}$

可知 ${\stackrel{\dot{}}{x}}_3,{\stackrel{\dot{}}{x}}_4$ 均有界，故 $x_3,x_4$ 一致连续。下面说明 $\underset{t\to \infty }{\lim }{x}_3=0$ ，为此考察函数 $x_3{x}_4$ 其导数 $\frac{\text{d}\left(x_3{x}_4\right)}{\text{d}t}=-k_3{\left|x_3\right|}^{1+{\alpha }_1}-k_4{x}_{4}sign\left(x_4\right){\left|x_4\right|}^{{\alpha }_2}+x_4^2$ 令

$\begin{array}{l}{h}_1\left(t\right)=-k_3{\left|x_3\right|}^{1+{\alpha }_1}\\ h_2\left(t\right)=-k_4{x}_{3}sign\left(x_4\right){\left|x_4\right|}^{{\alpha }_2}+x_4^2\end{array}$

由 $\underset{t\to \infty }{\lim }{x}_4=0$ ，有 ${\stackrel{\dot{}}{h}}_1\left(t\right)$ 有界，故 $h_1\left(t\right)$ 一致连续，且 $\underset{t\to \infty }{\lim }{h}_2\left(t\right)=0$ 。由Barbalat引理(17)及其推论，可知 $\underset{t\to \infty }{\lim }{x}_3=0$ ，故闭环系统有渐近稳定性。

对于系统 $\begin{array}{l}{\stackrel{\dot{}}{x}}_1=x_2\\ {\stackrel{\dot{}}{x}}_2=u\end{array}$ ，也可采用类似方法，即令

$u=-k_{1}sign\left(x_1\right){\left|x_1\right|}^{{\alpha }_1}-k_{2}sign\left(x_2\right){\left|x_2\right|}^{{\alpha }_2}$

可实现系统的全局渐近稳定。证明从略。

4. 系统仿真

仿真过程中的各项参数为：g = 9.8 m/s²；M = 5.0 kg；m = 1.0 kg；l = 0.5 m；

仿真起始时刻x(0) = 0.5米；摆杆的初始角度为0.3 rad；k₁ = 1，k₂ = 5，k₃ = 3，k₄ = 5.2仿真结果如下图2~5所示。

Figure 2. Car position control diagram

图2. 小车位置控制图

Figure 3. Control diagram of swing angle

图3. 摆角控制图

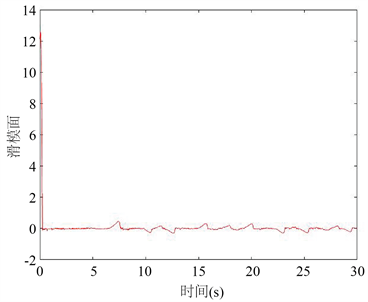
Figure 4. Sliding mode surface change diagram

图4. 滑模面变化图

Figure 5. Control output diagram

图5. 控制输出图

5. 结论

本文基于双积分链式控制理论，研究了轮式倒立摆的平衡控制方法。由仿真实验可知，在所设定的初始条件下，该控制算法精度高，可以缓解抖振现象，具有较好的稳定性。控制输入的超调也比较小。应用李雅普诺夫定理证明了该控制方法的收敛性和稳定性。单摆系统是一种应用较广的机械系统，所以该控制策略也可以应用到其他机械系统。