基于相关系数与自适应滤波的心率估计

Heart Rate Estimation Based on Correlation Coefficient and Adaptive Filtering

摘要: 近年来，基于光电容积脉搏波(PPG)实时监测心率受到各界的广泛关注，但由于在运动状态下光电容积脉搏波信号容易受到运动伪迹(MA)的叠加影响，尤其当运动幅度越大时，脉搏波信号产生的叠加干扰越严重，使得难以利用PPG信号准确计算出计心率值。为了保证能够从脉搏波信号中准确地估计心率值，为此提出一种去除脉搏波信号中运动伪迹的新算法CC-RLS，此算法利用复合归一化含噪脉搏波信号和均方根形式的加速度信号之间的相关系数法(CC)初步减少运动伪迹对PPG信号的叠加；选取合适的信号作为递归最小二乘(RLS)自适应滤波的输入信号再次滤除相关运动伪迹，增加了与心率相关的谱峰峰值，最终得到较为纯净的脉搏波信号，并且使用谱峰追踪算法进行实时心率估计。根据实验结果表明，相关系数法能够快速的消除运动伪迹谱峰峰值，并且在不同的运动状态下，该算法在10个PPG数据集上的心率估计误差较小、相比其他算法具有更少计算时间、较高的估计精度、算法稳定性高、鲁棒性强，并带来较强的实用价值。

Abstract: In recent years, real-time monitoring of heart rate based on photocapacitance pulse wave (PPG) has received widespread attention from various fields. However, due to the fact that the photocapaci-tance pulse wave signal is easily affected by the superposition of motion artifacts (MA) during exer-cise, especially when the amplitude of exercise is larger, the superposition interference generated by the pulse wave signal becomes more severe, making it difficult to accurately calculate the heart rate value using PPG signals. In order to ensure accurate estimation of heart rate values from pulse wave signals, a new algorithm CC-RLS is proposed to remove motion artifacts from pulse wave sig-nals. This algorithm utilizes the correlation coefficient method (CC) between composite normalized noisy pulse wave signals and root mean square acceleration signals to preliminarily reduce the su-perposition of motion artifacts on PPG signals; Selecting a suitable signal as the input signal for re-cursive least squares (RLS) adaptive filtering, the relevant motion artifacts are filtered again, in-creasing the spectral peak value related to heart rate, and finally obtaining a relatively pure pulse wave signal. The spectral peak tracking algorithm is used for real-time heart rate estimation. Ac-cording to the experimental results, the correlation coefficient method can quickly eliminate the peak values of motion artifact spectra. Moreover, under different motion states, the algorithm has smaller heart rate estimation errors on 10 PPG datasets, has less computational time, higher esti-mation accuracy, high algorithm stability, strong robustness, and brings strong practical value compared to other algorithms.

1. 引言

心率是衡量人们身体健康的重要生理参数，监测心率变化可以为人体亚健康状态提供科学依据。监测心率的方法目前主要使用的是心电图信号(ECG) [1] 和光电容积脉搏波信号(PPG) [2] ，心电信号在连续实时监测具有局限性，而光电容积脉搏波信号监测心率方便简易的优点备受青睐，检测设备多为智能手环、手表 [3] 等。但由于采集设备与受测者皮肤存在间隙，在运动过程中会使脉搏波波形被运动噪声叠加，心率计算发生偏差。因此，如何在不同MA的场景下仍能获得纯净的PPG信号是心率估计的一个重要研究方向。

现阶段消除MA的算法中，自适应滤波 [4] [5] 具有良好的滤波效果，此方法非常依赖参考信号，参考信号往往决定滤波的效果，自适应滤波通常和其他方法结合使用，如小波阈值去噪、经验模态分解(EMD) [6] 等方法。Wan C [7] 使用小波阈值与递归最小二乘(RLS)自适应滤波结合起来去除干扰信号，该方法在强MA条件下仍能保持较高的估计精度。Arunkumar K R [8] 采用递归最小二乘(RLS)和归一化最小均方(NLMS)自适应滤波器结合对PPG信号进行去噪。Islam M S [9] 提出一种基于约束递推最小二乘(cRLS)的去噪算法来消除PPG信号中的MA。Yang D [10] 提出自适应频谱噪声消除(ASNC)，用于去除PPG信号中的MA。独立分量分析(ICA) [11] 是一种经典的盲源分离算法。赵爱东 [12] 采用经验模态分解(EMD)结合ICA去除头部运动伪迹。Roy V [13] 通过ICA和规范相关分析(CCA)以及离散小波变换和平稳小波变换方法的组合，每一种组合方法都应用于脑电波运动伪迹抑制。Liu G [14] 提出一种基于支持向量机(SVR)和集合经验模态分解(EEMD)方法(SVR-EEMD)，该方法有效地解决“末端效应”。Zhang [15] 提出一种TROIKA的方法，先用奇异值分解将PPG信号分解为多个分量，使用加速度信号识别与MA相关的分量。去除分量后，对PPG信号与剩余分量进行稀疏信号重构，获得干净的PPG信号。此后Zhang引入一种称为JOSS的方法，提供了较低的平均误差。文武 [16] 运用奇异谱分析将矫正后的三轴加速度信号分组为不同频率成分的信号，作为三级快速横向递归最小二乘(FTRLS)算法的参考信号自适应消除运动伪迹，保留了重博波信息。Nathan V [17] 通过预测和更新过程使用粒子滤波，利用概率密度估计HR值。该算法通过校正异常值提高了估计精度。周光祥 [18] 通过小波变换对PPG信号进行去噪。王杰华 [19] 通过EMD和奇异值分解对PPG进行去噪。胡芳凝 [20] 提出一种基于快速滑动平均滤波的去噪算法。

基于上述算法，提出一种新算法CC-RLS消除PPG信号中的运动伪迹。首先计算含噪PPG信号和加速度信号不同延时下的相关系数，选择相关系数最大的含噪PPG信号和加速度信号，构造拟合加速度信号，使含噪PPG信号与拟合加速度信号的差与加速度信号的相关系数最小，得到较为纯净的信号。其次使用递归最小二乘(RLS)再次去除运动伪迹。结果表明，该算法取得较好的滤波效果，使用去除运动伪迹的脉搏波信号进行心率估计，最终得到较为准确的心率值。

2. 运动伪迹消除算法

检测者在不同程度的运动状态下，运动伪迹的叠加使脉搏波波形变得混乱无序，难以利用脉搏波信号计算心率值，为了消除运动伪迹，下文介绍了两种算法。

2.1. 信号预处理及相关性分析

设 $a_x\left(t\right),a_y\left(t\right),a_z\left(t\right)$ 为采集器采集的 $x,y,z$ 三个坐标轴的加速度信号， $y_1\left(t\right),y_2\left(t\right)$ 为传感器获得的两通道PPG信号，将 $y_1\left(t\right),y_2\left(t\right)$ 平均形成复合PPG信号 $y\left(t\right)$ ，能够减少随机噪声。将三轴加速度信号利用平方和的均方根形式转化为一维加速度信号 $a\left(t\right)$ ，一维加速度的具体表达式为 $a\left(t\right)=\sqrt{a_x{\left(t\right)}^2+a_y{\left(t\right)}^2+a_z{\left(t\right)}^2}$ ；可简化滤波器结构，提高滤波器参数收敛性。人在静止或运动状态下HR范围为30~200 ，单位为BPM/min，对应的频率范围为0.5~3.5 Hz，设计带通滤波器来消除 $y\left(t\right)$ 和 $a\left(t\right)$ 中超出频率范围内的干扰噪声，滤波器通带为0.5~3.5 Hz，并对 $y\left(t\right)$ 和 $a\left(t\right)$ 进行归一化统一量纲。图1为某窗口PPG信号时频域图，图1(a)~(b)信号变得更加“光滑”，图1(c)~(d)去除了正常HR范围以外的频率谱峰；“*”表示真实心率对应的谱峰，显然运动干扰带来的谱峰占据了信号频谱的主要最高部分。

(a) 复合PPG时域信号 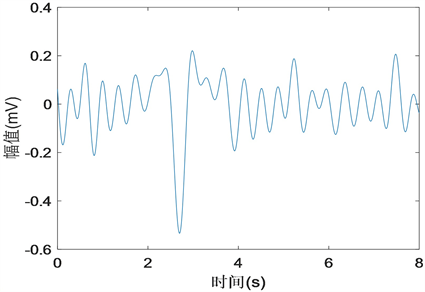(b) 归一化 + 带通滤波后复合PPG时域信号 (c) 复合PPG频域信号 (d) 归一化 + 带通滤波后复合PPG频域信号

Figure 1. Time frequency domain diagram of a certain window PPG signal

图1. 某窗口PPG信号时频域图

加速度 $a\left(t\right)$ 对心率影响存在延时性，为了确定延时长度，设延时长度为T，通过计算 $y\left(t+T\right)$ 和 $a\left(t\right)$ 的相关系数 $R\left(T\right)$ ，如图2所示，观察出 $R\left(T\right)$ 呈现一定的周期性，周期约为50。“*”表示 $T=40$ ，此时相关系数较大，相关性较大，下文提出相关系数法消除运动伪迹。

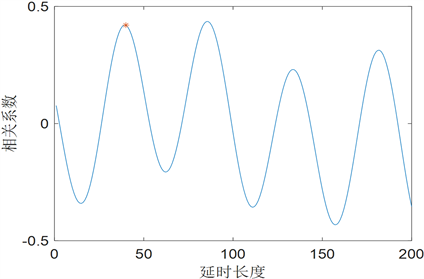
Figure 2. Curve plot of correlation coefficient about T

图2. 相关系数关于T的曲线图

2.2. 基于相关系数(CC)的噪声分离

加速度信号 $a\left(t\right)$ 造成运动伪迹在PPG信号的叠加，最大延时 $T=40$ ，通过将延时后的PPG信号减去加速度信号的一个倍数，消除这种叠加的影响，其中w为倍数，假设消除叠加影响后的PPG信号表示为 $Y\left(t\right)=y\left(t+40\right)-wa\left(t\right)$ ； $Y\left(t\right)$ 和 $a\left(t\right)$ 的相关系数为 $R_w\left(Y\left(t\right),a\left(t\right)\right)$ ，公式如下：

$\begin{array}{c}{R}_w\left(Y\left(t\right),a\left(t\right)\right)=\frac{\mathrm{cov}\left(Y\left(t\right),a\left(t\right)\right)}{\sqrt{D\left(Y\left(t\right)\right)}\sqrt{D\left(a\left(t\right)\right)}}\\ =\frac{C_1-w{C}_2}{\sqrt{C_3+w^2{C}_2-2w{C}_1}\sqrt{C_2}}\end{array}$ (1)

其中 $C_1$ 是 $y\left(t+40\right)$ 和 $a\left(t\right)$ 的协方差、 $C_2$ 是 $a\left(t\right)$ 的方差、 $C_3$ 是 $y\left(t+40\right)$ 的方差。

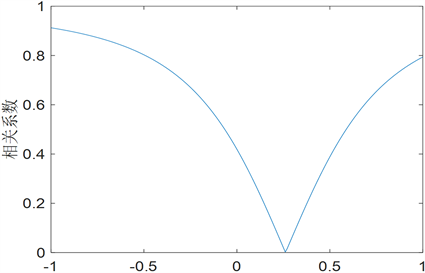
Figure 3. Graph of the objective function with respect to w

图3. 目标函数关于w的曲线图

确定叠加系数w，以相关系数 $R_w\left(Y\left(t\right),a\left(t\right)\right)$ 最小化为目标函数；目标函数越小，则去除运动伪迹的效果越好，目标函数公式如下：

$\underset{w}{\min }\frac{C_1-w{C}_2}{\sqrt{C_3+w^2{C}_2-2w{C}_1}\sqrt{C_2}}$ (2)

目标函数的图像如图3所示，经计算， $w=0.27$ 时相关系数 $R_w\left(Y\left(t\right),a\left(t\right)\right)=0.0022$ ，此时目标函数最小。

$y\left(t\right)$ 与 $Y\left(t\right)$ 的频谱图如下，“*”代表真实心率对应的谱峰，“o”代表运动干扰对应的谱峰。

(a) 原始信号的频谱图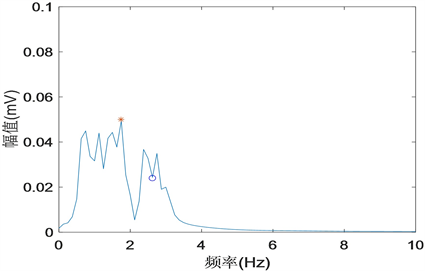(b) 消除叠加影响后信号的频谱图

Figure 4. Spectrum diagram of the original PPG signal and the signal after elimination of superposition

图4. 原始PPG信号与消除叠加后信号的频谱图

运动伪迹对PPG信号的干扰应为多个时刻加速度信号叠加的影响，人在静止状态下，频域上的最大谱峰即为真实心率所对应的谱峰 [21] 。图4(a)发现受到严重噪声干扰时，运动干扰的谱峰为信号频谱的最高谱峰，图4(b)发现经相关系数法后消除了对PPG信号影响最大的加速度信号的谱峰，消除了部分运动伪迹但没有完全消除；为了保证心率估算的准确性，考虑用自适应滤波对信号进行进一步去噪。

2.3. RLS自适应滤波去噪

加速度信号作为自适应滤波的参考信号来降低MA是目前广泛采用的方法，设 $\bar{a}\left(t\right)=wa\left(t\right)$ ，将 $\bar{a}\left(t\right)$ 作为自适应滤波器的参考信号， $Y\left(t\right)$ 作为自适应滤波器的期望信号。RLS自适应滤波算法是一种基于最小二乘准则的方法，具有速度收敛和稳定滤波的特点。RLS自适应滤波系统的框图如图5所示。

Figure 5. RLS Block diagram of adaptive filtering system

图5. RLS自适应滤波系统框图

$Y\left(t\right)$ 是滤波器的期望信号，滤波器输入信号为 $\bar{a}\left(t\right)={\left(\bar{a}\left(t\right),\bar{a}\left(t-1\right),\cdots ,\bar{a}\left(t-L+1\right)\right)}^{\text{T}}$ ，L是阶数，权系数为 $W\left(t\right)={\left(w_0\left(t\right),w_1\left(t\right),\cdots ,w_{L-1}\left(t\right)\right)}^{\text{T}}$ ，输出信号 $\bar{y}\left(t\right)={\displaystyle \underset{i=0}{\overset{L-1}{\sum }}{w}_i\left(t\right)\bar{a}\left(t-i\right)}$ ，误差信号为 $E\left(t\right)$ ，公式如下：

$E\left(t\right)=Y\left(t\right)-{\displaystyle \underset{i=0}{\overset{L-1}{\sum }}{w}_i\left(t\right)\bar{a}\left(t-i\right)}$ (3)

RLS是利用前 $t-1$ 及之前滤波器参数，对 $W\left(t\right)$ 不断更新，得到t时刻的参数，代价函数如下：

$S\left(t\right)={\displaystyle \underset{i=0}{\overset{t}{\sum }}{\lambda }^{t-i}}{\left|Y\left(i\right)-{\bar{a}}^{\text{T}}\left(t\right)w\left(t\right)\right|}^2$ (4)

其中 $0<\lambda <1$ 。

为使代价函数达到最小值，对权向量求导，得到的迭代公式：

$E\left(t\right)=Y\left(t\right)-{\bar{a}}^{\text{T}}\left(t\right)w\left(t-1\right)$

$R^{-1}\left(t\right)=R^{-1}\left(t-1\right)-\frac{R^{-1}\left(t-1\right)\bar{a}\left(t\right){\bar{a}}^{\text{T}}\left(t\right)R^{-1}\left(t-1\right)}{1+{\bar{a}}^{\text{T}}\left(t\right)R^{-1}\left(t-1\right)\bar{a}(\; t\; )}$

$w\left(t\right)=w\left(t-1\right)+R^{-1}\left(t\right)E\left(t\right)\bar{a}\left(t\right)$ (5)

以上提出的CC相关系数法与RLS自适应滤波相结合，消除运动伪迹对为HR估算的影响。图6为相关系数法CC与自适应滤波结合消除运动伪迹后的PPG频谱图，凸显了真实心率的谱峰，方便计算HR。

2.4. 基于频谱的心率估计

含噪PPG信号经过CC-RLS消除运动伪迹后，时域信号可能发生较大的变化，可能还有其他干扰信号的叠加，因此很难在时域中直接估计HR的值。故通过快速傅里叶变换(FFT)获得的PPG频谱图估计心率值；HR估计包括初始谱峰估计、谱峰选择、谱峰验证。

首先谱峰估计，设窗口为第i个 $\left(i=1,2,\cdots ,N\right)$ ，要求测试者在测试开始时前几秒保持静止，避免运动伪迹的影响。使用频谱估计心率，对消除运动伪迹的信号做FFT后，频谱自变量为频率，用s表示，对应的幅值用 $F_i\left(s\right)$ 表示，搜索信号频率谱的最大谱峰，该谱峰对应的频率为 $s_i^{*}$ 为估计心率的频率， ${\hat{H}}_i$ 为对应的心率，公式如下：

Figure 6. Frequency domain signal graph

图6. 频域信号图

$s_i^{*}=\arg \underset{s}{\max }{F}_i\left(s\right)$ (6)

${\hat{H}}_i=60s_i^{*}$ (7)

考虑到正常情况下人的心率不会发生骤变的情况，相邻窗口之间的心率具有一定的连续性。通过 $s_{i-1}^{*}$ 来确定当前窗口频率搜索的范围，当前位置范围为 $R=\left[s_{i-1}^{*}-\delta ,s_{i-1}^{*}+\delta \right]$ ； $\delta$ 为 $s_i^{*}$ 和 $s_{i-1}^{*}$ 的变化幅度的上限。

第二步谱峰选择，首先去除R以外的谱峰，其次在范围内选择大于最高谱峰40%的谱峰，选取前第二大、第三大谱峰作为候选谱峰，记候选谱峰频率为 $s_i^{*\left(m\right)}$ ， $m=1,2,3$ ；选择与 $s_{i-1}^{*}$ 最接近且满足条件 $\left|s_i^{*\left(m\right)}-s_{i-1}^{*}\right|\le \delta$ 的 $s_i^{*\left(m\right)}$ 作为当前时间窗口的心率，否则记 $s_i^{*}=s_{i-1}^{*}$ 。

上述算法可以准确计算一般情况下的心率值，但不排除某些极少数极端情况，运动伪迹的频率和PPG有效频率完全处于同频状态。此算法有可能把有效PPG频率滤除掉，这样计算心率会产生很大的偏差，故对心率进行修正。设窗口 $i-1$ 、 $i\left(i=1,2,\cdots ,N\right)$ 心率 ${\hat{H}}_{i-1}$ 与 ${\hat{H}}_i$ 变化最大值为 $\mu$ ，偏差较大的窗口心率修正公式如下：

${\hat{H}}_i=\{\begin{array}{ll}{\hat{H}}_{i-1}+\mu ,\hfill & {\hat{H}}_i-{\hat{H}}_{i-1}>\mu \hfill \\ {\hat{H}}_{i-1}-\mu ,\hfill & {\hat{H}}_i-{\hat{H}}_{i-1}<-\mu \hfill \\ {\hat{H}}_i\text{,}\hfill & 其他\hfill \end{array}$ (8)

其中 $\mu$ 是给定的一个参数。

3. 数值实验

为了验证CC-RLS算法消除运动伪迹的效果，用MATLAB R2020b进行仿真实验，并设置对比实验，进而说明本文所给的算法在去除运动伪迹具有有效性。

3.1. 数据集介绍

数据集来自2015年IEEE信号处理杯，数据集由12个训练集和10个测试集组成，每个数据集包含两个通道的PPG信号、三轴加速度信号和一个通道的ECG信号，对于每个检测者，通过两个带绿色LED (波长：515 nm)的脉搏血氧计从手腕记录双通道PPG信号。三轴加速器从手腕上记录了加速度信号；使用ECG传感器同时记录来自胸部的ECG信号，采样频率为125 Hz。在12个训练数据集记录过程中，检测者在跑步机上行走或跑步，时间H(分钟)与速度V(千米/小时)变化如下表1：

Table 1. Table of time and speed changes

表1. 时间与速度变化表

3.2. 参数设置

窗口长度为1000，步长为2秒。RLS自适应滤波器的阶数为N = 32，遗忘因子 $\lambda =0.999$ [22]。从真实HR值可以看出，相邻时间窗口的变化小于6 BPM。考虑到这些因素，取 $\delta =0.2$ ， $\mu =6$ 。

3.3. 评价指标选择

设 $H_i$ 为第i个时间窗口真实心率，第i个时间窗口真实心率为 ${\hat{H}}_i$ ，并设其绝对误差 ${\epsilon }_i={\hat{H}}_i-H_i$ ，相对误差 ${\epsilon }_{ri}=\frac{{\hat{H}}_i-H_i}{H_i}$ ； $\bar{\epsilon },{\bar{\epsilon }}_r$ 分别表示N个信号窗口绝对误差绝对值的平均和相对误差绝对值的平均，即 $\bar{\epsilon }=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left|{\epsilon }_i\right|}$ ， ${\bar{\epsilon }}_r=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left|{\epsilon }_{ri}\right|}$ ，并以此来作为衡量估计结果的标准。

3.4. 算法对比分析

根据实验结果的分析，将算法CC-RLS与其他论文提出的troika [23] 框架、joss [23] 框架及SSA + KS [24] 框架做对比，进行相关算法的评估，可见本算法具有较好的检测精度，评估方式为平均绝对误差( $\bar{\epsilon }$ )与平均相对误差( ${\bar{\epsilon }}_r$ )，使用10个相关样本进行实验得出数据如下表2，表3所示：

Table 2. Comparison results of Mean absolute error

表2. 平均绝对误差对比结果

Table 3. Comparison results of average relative error

表3. 平均相对误差对比结果

下图为各算法在10个数据集的平均绝对误差对比图，能够直观地反映出误差的整体水平。

以数据集第五个样本为例，图8为真实心率与估计心率的匹配追踪图。

4. 结果分析与讨论

表2和表3列出了其他算法和本文提出的算法在10个训练数据集上的平均绝对误差和平均相对误差。结果表明，在大多数据集中，CC-RLS的性能优于其他算法。而个别误差略高，但在可接受的范围内。

图7可看出CC-RLS算法平均绝对误差相较其他算法更小，在第10个数据集上误差最小。图8描述了受试者5心率估计值和真实值，CC-RLS算法估计值与真实值基本吻合，进一步说明了CC-RLS算法的良好性能，本文算法计算每个窗口的处理时间约为30 ms，所花费时间较少。

Figure 7. Comparison chart of Mean absolute error of each data set

图7. 各数据集的平均绝对误差对比图

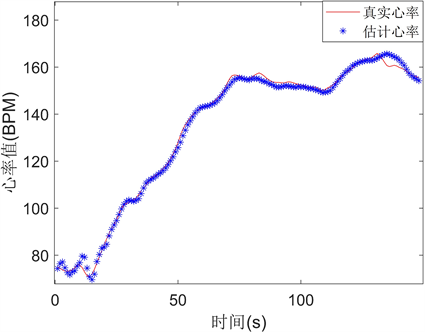
Figure 8. Matching pursuit chart of real heart rate and estimated heart rate

图8. 真实心率与估计心率的匹配追踪图

5. 总结

本文提出一种新的PPG信号去除运动伪迹的处理方法。此方法将PPG信号与加速度信号的相关系数联系起来，利用目标函数最小化求得最佳倍数，进而减少运动伪迹；结合RLS自适应滤波再次滤除运动伪迹，可以得到较理想的纯净PPG信号。此算法能够得到更加稳定的去噪，并且运算量更少，下一步将考虑增加w的维数提高算法的性能，简化计算量的同时也避免滤波器阶数选择和参数的影响。