1. 引言
泵车是现代建筑施工中不可或缺的机械装备,其工作稳定性直接影响施工质量。混凝土泵车臂架产生振动的因素包括发动机工作、液压系统泵源及泵送缸换向等,因此对其系统优化,达到减小和抑制臂架系统振动是泵车设计重点 [1] ,本文主要考虑液压系统泵源的流体脉动抑制。
产生于液压系统中的压力脉动,是由于容积式液压泵的结构原因,其输出是周期性的脉动流量,当遇到系统阻抗时形成的。通过应用实践表明,各种流体滤波器的安装,对减小泵的负载阻抗,增加对液压系统脉动压力衰减和抑制均具有明显的效果 [2] 。其中,结构耦合振动式气体消声原理为液压系统脉动控制提供了借鉴,该滤波器利用构件与流体的耦合共振将流体脉动能量转化为机械振动能量来控制和衰减,能在某一小频段范围内达到良好使用效果 [3] 。随后,有学者提出利用机械谐振式脉动补偿器来消减流体压力脉动。其思路是设计一种结构简单、灵巧的多自由度的机械谐振机构,在较宽频率范围内,使任意频率成份的流体脉动都可以对应一个与之谐振的吸振系统,将液压脉动最大限度地转换成机械振动,再通过内部阻尼消耗振动能量,则可获得广谱高效的液压脉动抑制效果 [4] 。试验结果表明,该类型的脉动衰减器在50~1000 Hz的范围内,插入损失可达10 dB以上,流体脉动抑制效果较好 [5] 。但该谐振式滤波器对流体脉动频率响应灵敏度要差,且系统压力损失大。
近来,有研究者提出使用张紧柔性膜来反射低频噪声的想法。这是一种被动噪声控制方法,利用预张拉柔性膜片与噪声的耦合振动来消除噪音,其结构原理是使用容器支撑的高度张紧膜来实现 [6] 。由于该装置类似于一个鼓,所以称之为鼓状消音器或鼓式消声器。通过对膜的真空模态响应分析发现,前两阶模态起主导作用 [7] 。同时其研究结果表明,在膜片上施加高张力有利于促进膜的低阶模态的响应,使系统更能有效地反射声音。经声反射和透射损失光谱显示,在声音几乎完全被反射的频率上出现了很多峰值。在两个相邻峰的频率之间,如果选择合适的膜片参数,膜片性能可以保持在一个相当高的水平,并能表现出良好的消声性能 [8] 。
本文将结合鼓式消声器的工作机理,顾及滤波器适应液压系统的高压、稳态大流量、低压缩性及耐腐蚀等工况要求,设计一种仿生膜片式流体滤波器,分析其工作机理并建立动力学模型,初步确定单膜片式流体滤波器结构参数,仿真分析其动态特性,并通过试验验证理论分析的正确性。
2. 膜片式流体滤波器工作机理
动力吸振器的工作机理表明,具有固定振动频率的附加“弹簧–质量”系统与流体系统的激励源频率相近时,会产生系统的共振,并引起反共振现象,从而衰减液压系统的振动能量 [9] ,机理类似于赫姆霍兹共鸣器,不同是动力吸振器将流体脉动能量转化为机械振动方式衰减。
本研究仿照耳蜗听觉原理,在滤波器内用轻巧的柔性膜片来替代动力吸振器中的机械振动元件 [10] ,设计成一种灵巧的仿生膜谐振机构,从而在流体系统中实现小巧高效滤波效果,是我们的研究目标。
为研究方便,我们只对单一频率的仿生膜片进行振动情况研究,然后逐一推广。如图1所示,膜片式流体滤波器主要由滤波器壳体、静压平衡腔、柔性膜片及阻尼平衡孔组成。被张紧的柔性膜片为圆形,周边固定并受到径向的预张拉力。受张力的柔性膜片将主油路与静压平衡油腔隔开,中间通过静压阻尼平衡油孔联通,以此达到流体静压平衡的目的。单块柔性膜片与流体环境形成“质量–弹簧–阻尼”振动系统,在某一频段范围内能够产生共振响应。因此,如果在滤波器内安装不同结构尺寸的柔性膜片,就能在多频段范围内产生共振响应,同时衰减多个振动频率,取得广谱滤波效果。

Figure 1. Working principle of diaphragm type fluid filter
图1. 膜片式流体滤波器工作原理
膜片式流体滤波器它与普通结构振动式流体滤波器的区别在于:用轻盈的预张拉柔性膜片取代了刚性结构元件,使滤波器结构更精致,从而减小了滤波器的质量和结构体积。此外,柔性膜片比刚性振动体振动频率范围更大,从而使其滤波频域更宽,对流体系统不同工况的适应性更强。
本研究中的柔性膜片是一种超弹性橡胶材料,其是一种具有超长分子链的高分子聚合物,具有超强的弹性变形能力,其最大延伸率可达500%~1000%,且变形后复原能力强 [11] 。
为了能准确的对超弹性橡胶材料进行弹性变形的力学性能分析,需要建立其本构关系。橡胶在等温条件下的弹性变形,可用一种应变能函数W描述,它反应的是材料的变形状态函数,函数所包含的状态参数可通过试验研究确定。通常,材料的应变能函数W可由三个定值应变量I1、I2、I3描述为 [12] :
(1)
其中三个定值应变量I1、I2、I3分别为:
(2)
式中,λ为空间状态下的伸长率,即:
,其中L0为橡胶自由状态下的初始长度;λ的下标1、2、3分别代表空间X、Y、Z轴3个方向。因为橡胶材料在Z轴上的压缩变形量可忽略不计,故I3 = 1,因此对于式(1),可用下述公式来描述 [13] :
(3)
式中,C1为材料常数,该关系式表达简单,只能反应材料在单向拉伸变形40%应变范围内及剪切变形90%应变范围内的状态。
研究表明,橡胶是一种各向同性材料。设橡胶弹性膜片在张拉变形前的半径为R,厚度为h,质量密度为ρ。预张拉变形后,膜片的半径为Rf,则膜片张拉变形率为δ = Rf/R。由于柔性薄膜没有结构刚度,可以采用预张拉后柔性薄膜的预应力作为刚度,用超弹性膜理论来描述柔性膜的振动变形。
在空间直角坐标系中,设一微小单元柔性膜在点P处发生张拉变形,r为微小单元膜在点P处的半径,θ为膜在点P处与X轴的夹角。根据文献 [13] 的推导,因此式(3)的定值应变I1可以写为:
(4)
我们假定流体脉动压力Ph(t)作用在柔性膜上的方向是横向的,即与Z轴平行,因此膜在振动时平面位移分量很小,可忽略不计,因此柔性膜的振动弹性势能可表示为:
(5)
同时,在张拉力F和脉动压力Ph(t)的作用下,柔性膜的动能T和应变能函数We分别为:
(6)
(7)
式中,ρ为膜的单位质量密度,由于柔性薄膜是不可压缩的,因此其单位质量密度在膜变形状态中保持恒定。
是指柔性膜在外力作用下的体积变化,Vf为变形后膜包围的体积,V0为变形前膜包围的体积,由于张拉前膜是平整的,固有V0 = 0。因此,膜振动的拉格朗日函数表达式为:
(8)
上式中,忽略阻尼作用和外部负载影响,对膜沿Z轴方向的横向振动进行处理,可得膜的横向振动线性化方程为:
(9)
令
,采用贝塞尔方程求解可得到获得膜沿Z轴方向的横向振动微分方程的解为:
(10)
式中,Amn为振动模态的幅度;n为圆周方向的振动模态波数;
为(m, n)阶的固有圆周频率;Jn为第一类贝塞尔函数。
因此,可求得预张拉膜的固有圆周频率为:
(11)
则预张拉膜的固有振动频率fmn为:
(12)
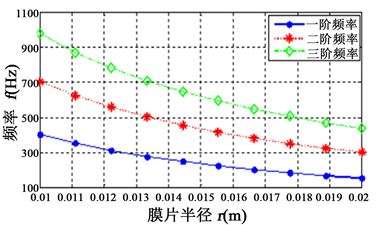
Figure 2. The relationship between the first three vibration frequencies of flexible membranes and their radius
图2. 柔性膜前三阶振动频率与其半径的关系
设柔性膜的预张拉伸长率δ = 1.1,质量密度
,材料常数C1 = 0.5 MPa,代入式(12)可解得柔性膜前三阶振动频率fmn与其半径的关系如图2所示。
图2显示,当柔性膜的预张拉伸长率(简称拉伸率)即张力一定时,预张拉膜固有振动频率随着膜片半径的增加而逐步降低,达到一定程度后并逐步趋于平缓。同时,其前一、二和三阶频率基本成倍频关系。
此外,柔性膜的预张拉伸长率也是影响膜片固有频率的重要因素 [14] 。参照式(12),如果δ趋于无穷大,则膜片固有频率收敛于下式:
(13)
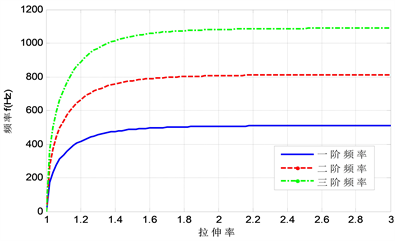
Figure 3. The influence of membrane stretching rate on the natural frequency of the membrane
图3. 膜的拉伸率对膜片固有频率的影响
图3为膜片固有频率与预张拉伸长率的关系曲线图。图中可看出,当拉伸率处于1到1.6之间时,膜片固有频率随着拉伸率的增大而顺速增加,之后变化趋缓。当拉伸率超过2后,膜片固有频率变化不明显,基本趋于定值。为研究方便,本文选取膜片的拉伸率δ = 1.1进行研究。
3. 膜片式流体滤波器流固耦合动力学分析
如图4所示,假设高度为h的流体通道壁有一直径为L的柔性膜片,膜片将流体通道与深度为hc的充液容腔隔开,中间通过直径为d的阻尼孔相通。为简化分析,在理论上我们假定柔性膜片是二维的。从滤波器通道左边进入一脉动压力能,导致柔性膜发生振动。首先,我们限定流体脉动频率低于滤波器的第一截频c/2h,现在我们要研究的问题是被反射的脉动能占多少?传递到下流通道有多少?膜振动内部摩擦损耗了多少?能量的反射系数和吸收系数分别用β和α表示,TL代表传递损失,同时,以下所用参数都通过了归一化无量纲处理。
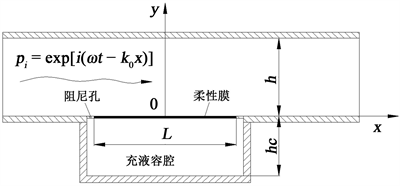
Figure 4. Structural schematic diagram of single diaphragm fluid filter
图4. 单膜片式流体滤波器结构原理图
在图4中,设坐标原点位于柔性膜片的中心,柔性膜处于
的范围内,振动状态下,膜片厚度b(x)随x变化,因此对其进行平均值的归一化处理后有:
(14)
因此,膜片的质量可写为:
(15)
式中,M0是柔性膜的平均质量。在脉动压力
作用下,膜片产生振动,如果加载到膜片上的总负载记为
,可以用下面这个方程来描述此流固耦合的动力学 [15] :
(16)
式中,η为局部膜片的振动位移,位移由
计算所得;T为膜片装配时的预张拉力,
;流体加载项
可以分成三个部分,一是由在管道这边的膜片诱发的压力
,第二个在容腔侧的膜片诱发的压力
。第三部分,是从阻尼孔反射的压力
。
可以通过对所有管道声音模态
求和得到。

Table 1. Basic parameters for theoretical calculation and simulation analysis of diaphragm fluid filters
表1. 膜片式流体滤波器理论计算及仿真分析的基本参数
所以,系统的插入损失可计算为:
(17)
式中,
是充液容腔室的峰值传输损耗,Vc是与hc相关的充液容腔体积。
参照表1的基本参数,对预张拉力下的柔性膜片进行系统流固耦合的传递损失进行仿真分析,得到如图5的结果。
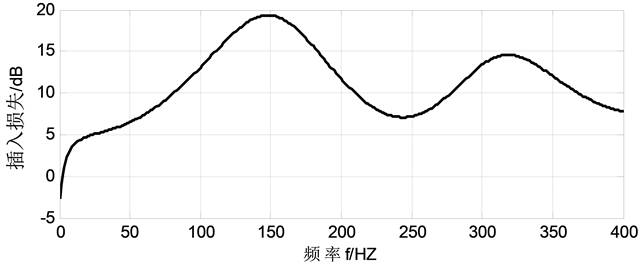
Figure 5. Dynamic modeling of single diaphragm fluid filter insertion loss simulation results
图5. 单膜片式流体滤波器动力学建模插入损失仿真结果
图中仿真结果表明,滤波器在基频150 Hz及其2倍频300 Hz附近,对流体脉动具有明显的衰减作用,基频处的插入损失接近20 dB,2倍频处的插入损失接近15 dB。同时基频在115~180 Hz范围内,压力脉动衰减达到15 dB以上,说明滤波具有一定的带宽。
4. 膜片式流体滤波器性能测试分析
为降低滤波器对系统的压力损耗,减轻结构振动体的自身质量是我们的首要考虑。因此,按照表1的参数,用柔性膜片替代弹性薄板,我们设计了单膜片式流体滤波器样机,并在流体脉动测试试验台上进行了测试试验。试验中调定泵转速为1020 r/min,理论计算流体压力脉动基频为153 Hz,与仿真计算的150 Hz结果接近。试验测试结果分别如图6及表2所示。
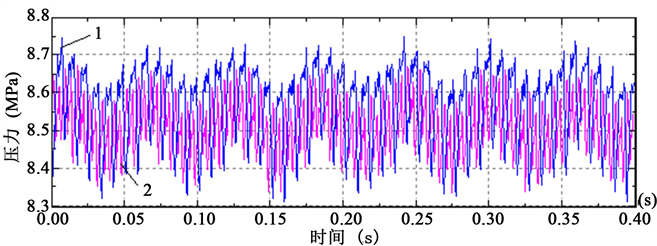 1. 滤波器入口压力p1 2. 滤波器出口压力p2
1. 滤波器入口压力p1 2. 滤波器出口压力p2
Figure 6. Time domain signal diagram of filter inlet pressure p1 and outlet pressure p2 at pump speed 1020 r/min
图6. 泵转速1020 r/min时滤波器入口压力p1及出口压力p2时域信号图

Table 2. Test data and calculation results at pump speed of 1020 r/min
表2. 泵转速1020 r/min时的测试数据及计算结果
图6中,1为滤波器入口的压力时域曲线,2为滤波器出口的压力时域曲线。图示结果明显看出,膜片式滤波器出口的时域曲线与入口压力时域曲线波形基本一致,没有明显区别,说明数据信号没有外界干扰。表2的数据结果表明,系统的脉动压力经过滤波器衰减后,改善比较明显,压力脉动波动范围由滤波前的0.44 MPa降到0.33 MPa,脉动率由5.1%降到4.0%,压力脉动衰减率达到21.6%,具有较好的滤波效果。与薄板振动式流体滤波器测试结果相比,系统的能量损失更小。
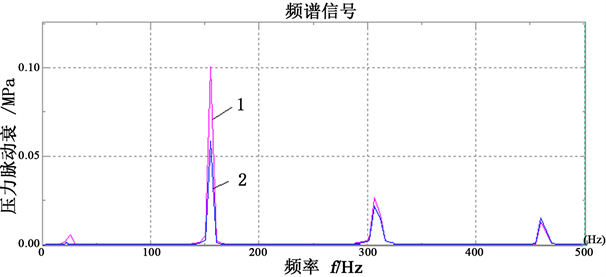 1. 滤波器入口端压力脉动频域曲线2. 滤波器出口端压力脉动频域曲线
1. 滤波器入口端压力脉动频域曲线2. 滤波器出口端压力脉动频域曲线
Figure 7. Frequency domain signal diagram at pump speed of 1020 r/min
图7. 泵转速1020 r/min时的频域信号图
图7为的压力信号的频谱分析。图示结果表明,在频率约155.7 Hz和312.2 Hz处,滤波器与流体将形成共振,这与图5的仿真结果接近。在基频155.7 Hz处,压力脉动频域幅值由0.097 MPa降到了0.065 MPa,衰减幅度33%,与时域信号分析结果基本一致,证明滤波器的理论建模及仿真结果是正确的。
5. 结论
论文仿照耳蜗听觉原理,用柔性膜片替代结构振动式流体滤波器器中的机械振动元件,设计了一种灵巧的仿生膜谐振机构,研制了一种单膜片式流体滤波器。分析了膜片式流体滤波器工作机理,建立了预拉伸柔性膜片动力学模型,仿真计算了预张拉力下柔性膜片流体滤波器在流固耦合作用下的传递损失。在流体脉动测试试验台上的试验结果表明,在滤波器工作基频处的插入损失接近20 dB,2倍频处的插入损失接近15 dB。同时在频率115~180 Hz范围内,压力脉动衰减也达到15 dB以上,说明滤波器对滤波频率的自适应性,具有较好的工程应用价值。后续将结合薄板振动式流体滤波器和膜片式流体滤波器各自的性能特点,制成刚柔结合的振动子系统,降低系统能量损耗,提高脉动衰减效果。