1. 引言
混凝土强度是混凝土质量控制的核心内容,是结构设计和施工的重要依据,是混凝土最重要的性能之一。混凝土的质量,直接关系到分项工程、分部工程以及单位工程的评定验收。混凝土的原材料处理常用的水泥以外,新出现了球状水泥、调粒水泥、活化水泥等,而矿渣、粉煤灰、沸石等超细掺合料及硅粉等,成为高强度混凝土中不可缺少的组分 [1] 。超强塑化剂、高效减水剂等外加剂的应用也越来越普遍。所有这些使得混凝土的组成更加复杂,性能更为优越,适应性更强,应用范围更广泛 [2] 。
一般来说,混凝土抗压强度是对混凝土试件进行28 d标准养护后,通过测试获得的,但混凝土强度的测试过程非常复杂且费时,即使试验结果不能满足规定强度,混凝土强度也不能提高。因此,混凝土抗压强度早期预测具有重要研究意义 [3] 。本文主要研究混凝土与水泥、高炉矿渣、粉煤灰、水、高效减水剂、粗骨料和细骨料以及龄期之间的线性关系,当然线性模型只是最简单和基础的模型,BP神经网络在建立非线性模型方面有非常好的效果 [4] ,但依据本学期学习的内容,本文只研究了线性关系,也取得了比较好的效果。
2. 模型理论
本文主要做的是线性回归分析,标准的线性回归模型是:
通常用于描述响应变量
与预测变量
之间的线性关系,
是需要估计的参数。下面介绍拟合此模型的方法。
2.1. 最小二乘回归
最小二乘法是求解线性回归模型最经典的方法,它的主要通过最小化RSS,
从而得到
。
对于n组观测数据,则需要拟合下列的线性回归方程组:
它可以表示成矩阵的形式:
,对于求解出最小的RSS,即关于求解
值,一般采用梯度下降法或者牛顿法。可以得到它的算法是:
其中
可逆,则要求
且特征不冗余。
2.2. 最优子集选择
最优子集选择是对p各预测变量的所有可能线性组合分别使用最小二乘回归进行拟合。对含有一个预测变量的模型,拟合p个模型;对含有两个预测变量的模型,拟合
个模型,以此类推。最后在所有可能的模型中选择最优模型 [5] 。它的算法过程是:对于
;k取每一个值都会生成相应数量
个模型,从中挑出RSS最小或R方最大的模型,记为
;再根据交叉验证预测误差、
(残差平方和)、BIC或者调整的R方找出最优的模型。其中
d表示预测变量个数。
Cp统计量是测试均方误差的无偏估计,所以测试误差较低的模型Cp取值也比较低,因此,可以通过选择具有较低Cp的模型作为最优模型;AIC是赤池信息准则,它适用于许多极大似然法进行拟合的模型,对于最小二乘模型Cp与AIC是成正比的;BIC是从贝叶斯信息准则,它通常给包含多个变量的模型施以较重的惩罚,所以与Cp相比,得到的模型规模更小 [5] 。以上三个统计量都是选择值最小的模型作为最优模型。
调整的R2是另一种对一系列具有不同变量个数的模型进行选择的方法,它定义为:
其中
。它的使用准则是调整的R2值越大,模型测试误差越小,因此选择值最大的模型作为最优模型。
2.3. 岭回归
岭回归系数估计值
通过最小化下式得到:
其中
是压缩惩罚,在机器学习中又叫做正则项,可以通过控制
的大小来调节模型的复杂度,当
时,惩罚项不产生作用,岭回归与最小二乘估计结果相同,随着
,压缩惩罚项的影响力增加,岭回归系数估计值越来越接近于0。
岭回归的系数估计问题等价于求解以下问题:
得到的模型估计是:
与最小二乘相比,岭回归的优势在于它综合权衡了误差与方差。随着
的增加,岭回归拟合效果的光滑度降低,虽然方差降低,但偏差在增大。而岭回归的劣势在于它无法做子集选择,它的最终模型包含全部的变量。
2.4. Lasso回归
Lasso的系数估计值
通过求解下式的最小值得到:
岭回归的惩罚项采用的是二范数,而Lasso的惩罚项采用的1范数,它定义为
。Lasso估计也将系数估计值往0的方向进行缩减,而且,当参数
足够大时,惩罚项具有将其中一些系数估计值强制设定为0的作用。所以Lasso可以完成变量选择,它得到了稀疏模型——只包含所有变量的一个子集的模型 [5] 。
Lasso的系数估计也等价于求解以下问题:
当n = p时,Lasso估计形式如下:
3. 实证分析
3.1. 数据介绍
3.1.1. 数据来源说明
本文所用的数据集来源于机器学习存储库(UIC),由台湾中华大学土木工程系叶毅成教授捐赠的混凝土抗压强度数据集。数据是由实验室测定的在特定龄期(天)下给定混合物的实际混凝土抗压强度(MPa),混凝土的成分包括水泥、高炉矿渣、粉煤灰、水、高效减水剂、粗骨料和细骨料。数据为原始形式(未缩放)。本文使用R软件对数据进行分析。
3.1.2. 数据变量说明
该数据集一共有9个变量,其中预测变量8个,响应变量1个,样本有1030个,没有缺失值,而且所有变量都是定量变量,具体变量信息见表1。
3.1.3. 描述性分析
对每个变量做描述性统计分析,得到的表2是各变量的最小值、第一四分位数、中位数、均值、第三四分位数、最大值。最小值和最大值体现了数据的波动范围,而它们的差值大小可以初步判断数据的波动大小,均值和中位数分别是在做参数估计和非参数估计使用的重要统计量,而分位数也是我们在估计位置参数时常用到的统计量。
相关系数矩阵热图用来判断两个变量之间的线性相关性,蓝色程度越深表示正相关性越强,红色程度越深表示负相关性越强。从图1可以看出X4和X5两个变量,即混合物中水的含量和高效减水剂的含量之间有较强的负相关性,在后续做线性回归时,可以考虑将其中一个用另一个线性表出。变量X3和X6,变量X8和X6之间的相关系数接近于0,即在建模的时候可以考虑混合物中粉煤灰的含量与粗骨料的含量相互独立,粗骨灰的含量与混凝土的龄期相互独立。
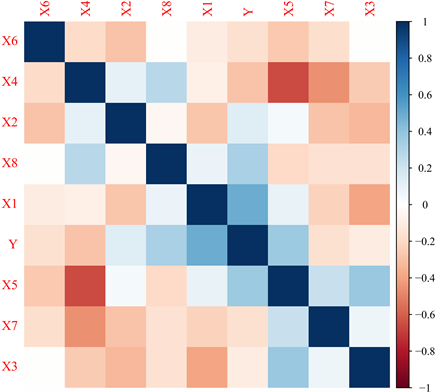
Figure 1. Heat map of correlation coefficient matrix
图1. 相关系数矩阵热图
在回归模型建立过程中,我们先划分数据的训练集和测试集,在训练集上拟合模型,在测试集上做预测,然后用均方误差评价模型效果。本文将2/3的数据作为训练集,1/3的数据作为测试集,见表3。
3.2. 最小二乘法
做简单的线性回归分析,先用最小二乘法拟合多元线性模型,首先得到的是表4模型的描述统计数据,分别是残差的最小值、分位数、最大值。

Table 4. Residual data for model 1
表4. 模型1的残差数据
表5是初始模型拟合结果,Estimate是回归参数的估计,它包括了常数项系数和预测变量系数,所以初始模型为:
Std.Error为回归参数的标准误,t value表示检验t值,Pr(>|t|)是t检验的P值。“***”说明极为显著,“**”说明高度显著,“*”说明显著,“.”说明不太显著,没有记号为不显著。所以,从表5可以看出拟合出的模型所有变量的系数都是显著的。

Table 5. Estimation of regression parameters for model 1
表5. 模型1的回归参数估计
表6是关于模型拟合效果的估计,虽然从检验的P值看出该模型估计是显著的,但通过R2和调整的R2可以看出,模型的拟合度并不高,只达到了0.62,模型还有望调整,使得模型具有更高的拟合度和预测精度。

Table 6. The effect of the fit of model 1
表6. 模型1的拟合效果
绘制模型的拟合效果图可以观察到很多改进方向,图3的第一行第一列是残差拟合图,它是模型拟合值与残差之间的散点图,红色线条表示二者关系的平滑曲线。若满足线性假设,二者应该不存在任何趋势性的关系,即红色线条应该与y = 0基本重合。从图中观察,红色线条大致与y = 0重合,但是散点图呈现倒漏斗形状,并不是均匀地分布在y = 0周围,可以考虑误差项的异方差性。
Q-Q图它可以检验数据序列是否满足某种概率分布,它将对应分布的概率分位数作为横坐标、数据序列的分位数作为纵坐标作成散点图,若该数据序列满足该概率分布,则散点的趋势线应该与某条直线基本重合。图2的第一行第二列是模型1的正态Q-Q图,可以看出散点的趋势与y = x是基本重合的,认为总体上看,模型1的残差大致服从标准正态分布。

Figure 2. Residual fit plot for model 1
图2. 模型1的拟合效果图
若模型满足同方差假设,则拟合值处于不同位置时残差的分布范围应该基本相同,即没有明显的集聚性或离散性,这一点可以通过观察残差–拟合图散点的离散程度,但更直观地是通过观察尺度–位置图。该图的纵坐标为标准化残差绝对值的平方根。若满足假设,则趋势线应该基本呈水平状。图2的第二行第一列是模型1的尺度–位置图,可以看出趋势线是呈缓慢上升状的,得到与残差拟合图相似的结论,即模型的误差项存在异方差性。
图形只能作为我们猜想的一个依据,在下结论之前我们需要做严格的假设检验。做Shapiro-Wilk检验:得到的P值是0.01341,在0.05的置信水平下拒绝原假设,认为残差服从正态分布。做异方差检验:得到的P值 < 2.22*10−16,在0.05的置信水平下拒绝原假设,认为模型是存在异方差性的。Durbin-Watson检验可以判断残差是否存在一阶自相关,即检验模型是否满足独立性假设,得到的P值 < 0.05,在0.05的置信水平下拒绝原假设,认为模型的残差是不存在一阶自相关性的。方差膨胀系数(VIF)可以用来检验自变量之间是否具有多重共线性。自变量对应的VIF越大,说明其越有可能与其他自变量存在多重共线性。如果自变量之间存在多重共线性,即某个特征可以有其他自变量线性表出,这会增大解的不确定性,可能导致最后与真实的β差别很大,或解的取值范围变大。我们通过上一节特征之间的相关矩阵发现X4与X5是存在线性相关的可能性的。从另一个方面,我们查看特征的方差膨胀系数(VIF),其中
结果如表7所示,发现膨胀系数最高的是X1,而剩下的变量X2、X3、X4、X7都存在较高的方差膨胀系数。

Table 7. Characteristic expansion factor for model 1
表7. 模型1的特征膨胀因子
线性回归中一个重要的假设是误差项的方差是恒定的,即
。线性模型中的假设检验和标准误差、置信区间计算都依赖于这一假设,但我们从前面的分析已经知道,误差项是存在异方差性的。因此考虑用凹函数对响应变量做变换,取响应变量为log(Y),得到的模型结果显示R2降低到了0.5615,说明取对数并没有使得模型的拟合效果更好。另一个消除异方差性的方法是使用加权最小二乘法拟合模型,加权最小二乘的基本思想是对原模型进行加权,即对较小的残差平方赋予较大的权数,对较大的残差平方赋予较小的权数,使之变成一个新的不存在异方差性的模型,然后再使用不同的最小二乘法估计模型参数。用加权最小二乘法拟合模型得到了模型2,它有一个非常理想的结果,如表8中的数据所示,模型显著,且拟合度达到了0.9052。表9是各变量和常数项的系数估计。

Table 8. The effect of the fit of model 2
表8. 模型2的拟合效果

Table 9. Values of fitted coefficients for model 2
表9. 模型2的拟合系数值
我们在测试集上对上面两个模型进行预测,计算模型预测值与真实值之间的均方误差(MSE),得到的结果如表10所示,可以看出模型1的均方误差要更小,即预测误差更小,这说明不能只用拟合效果来判断模型的好坏,这可能会出现过拟合的情况。

Table 10. Mean square error values for the two models
表10. 两个模型的均方误差值
3.3. 最优子集选择
用最优子集选择法估计线性回归模型参数具有更好的解释性,它实现了最优预测变量子集的筛选,得到了表11的结果,第1个模型只包含变量X1,第2个模型包含变量X1、X5,第3个模型包含变量X1、X5、X8,第4个模型包含变量X1、X2、X4、X8,第5个模型包含变量X1、X2、X3、X4、X8,第6个模型包含变量X1、X2、X3、X4、X5、X8,第7个模型包含变量X1、X2、X3、X4、X5、X6、X8,第8个模型包含所有变量。

Table 11. Models for optimal subset selection
表11. 最优子集选择的模型
评价模型的指标是R2,RSS,调整的R2,Cp(AIC)或者BIC,其中R2和调整的R2越大,模型拟合度越高,RSS,Cp,BIC越小,模型拟合度越高。从表12随着变量个数的增加,各统计量都得到改善,依照每一个统计量的数据选择了最优的子集个数,图3中的红色点表示各统计量选择的最优结果。结果显示选择6个特征是最优的。

Table 12. Model statistics for optimal subset selection
表12. 最优子集选择的模型统计量

Figure 3. Model selection results for each statistic
图3. 各统计量的模型选择结果
K折交叉验证法能够准确估计检验误差,它的基本原理是将观测数据随机地分为K个大小一致的组,或者说折。第一折作为测试集,然后剩下的K-1折上拟合模型,重复这个步骤K次,每一次在不同的K-1折上拟合模型,每一次拟合都会得到一个均方误差,K折的CV估计就是这些均方误差再求均值得到。用K折交叉验证法做最优子集选择,得到的结果是选择前6个特征的均方误差为109.1655,是最优的模型。
对整个数据集用最优子集选择,获得5个变量的参数估计结果汇总在表13中,所以我们通过最优子集法得到的模型是:

Table 13. Coefficients of the variables of the optimal subset method
表13. 最优子集法的各变量系数
3.4. 压缩估计
3.4.1. 岭回归
在做岭回归时,同样也是考虑使用交叉验证来调节参数λ,要注意的是使用岭回归要先对数据进行标准化,这里使用glmnet()函数在默认设置下,已经将所有变量进行了标准化。图4是10组子样本的交叉验证绘制CV曲线图寻找最佳的惩罚函数系数λ。采用最小MSE取值113.5488对应的
,对应8个解释变量。
用最优的λ建立岭回归模型,得到的变量系数见表14,所以我们建立第4个模型:

Figure 4. CV cross-validation plot for ridge regression
图4. 岭回归的CV交叉验证图

Table 14. Ridge regression model coefficients
表14. 岭回归模型系数
3.4.2. Lasso回归
与岭回归相比,当最小二乘回归出现较大方差时,Lasso以牺牲偏差为代价去降低方差,从而得到更为精确的预测结果。Lasso的优势是:Lasso的系数估计是稀疏的,它可以实现特征选择,因此得到的模型更容易解释。我们同样是使用10折交叉验证来调节最优的参数λ,图5是10组子样本的交叉验证绘制CV曲线图寻找最佳的惩罚函数系数λ。可以看到模型实现了特征选择,在只包含6个变量时模型就可以达到最优了。最小的均方误差是112.6013,它对应的λ是
。
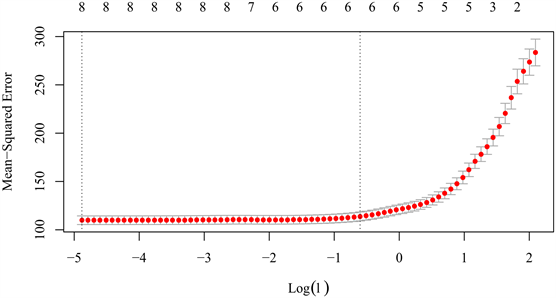
Figure 5. Lasso’s cross-validation plot
图5. Lasso的交叉验证图
用最优的λ建立岭回归模型,得到的变量系数见表15,所以我们建立第6个模型:

Table 15. Ridge regression model coefficients
表15. 岭回归模型系数
3.5. 模型的选择
综合上述的5个模型,表16是各模型的均方误差对比结果,可以看到选择第三个模型是最优的。

Table 16. Comparison of mean square error of models
表16. 模型的均方误差对比
4. 结论
本文对混凝土的抗压数据做线性回归分析,首先对数据集进行划分,然后采用多种参数估计方法来估计模型的系数,最后通过预测均方误差来选择最优的模型。
在用最经典的最小二乘法估计系数时发现模型的拟合度并不高,因此对多元线性回归模型进行模型诊断,首先考虑了误差项的异方差性,第一种解决办法是对因变量取对数后再进行简单的最小二乘回归方法进行拟合,发现模型的拟合效果和预测效果都没有得到提升;第二种解决办法是使用加权最小二乘回归方法进行拟合,得到了很高的拟合度,预测效果并不如简单的最小二乘回归方法,但是相差不是很大,所以相比较之下也可以考虑使用模型2来拟合数据。
考虑各变量之间可能存在共线性,解决办法是做最优子集选择。最优子集选择是通过选择最优或者说对模型有很大贡献率的特征子集来提高模型的拟合度的,选择最优模型参考的统计量是Cp,AIC,BIC和调整的R2,在训练模型是时候使用交叉验证法提高模型的准确度。得到的结果是:选择6个变量作为最优的模型的预测变量,计算模型的均方误差发现模型的预测效果还是有所提升的。
岭回归和Lasso都属于压缩估计的方法,它们通过对系数进行约束或加惩罚项的技巧对模型进行拟合,就是说将系数的估计值往0的方向压缩,这会提升拟合效果,Lasso的另一个优势是可以做特征选择,拟合结果显示,模型的预测均方误差并没有下降非常的多。
综合所有方法得到的结论是压缩估计都没有很好地提高模型的预测效果,最优的模型是做子集选择。
当然,模型还有很多改进的空间,由于本文使用的数据集的特征个数并不算多,做数据降维的效果也并不理想,没办法达到降维的效果。但是各特征之间的关系还是可以再进一步考虑的,比如相关性很强的两个特征可以通过线性组合等方式把一个两个特征变成一个新的特征。