基于整体最小二乘法的点云线性拟合及比对方法研究

Linear Fitting and Comparison Method of Point Cloud Based on Total Least Squares

摘要: 为解决建筑测绘领域点云数据矢量转化及比对方式的缺失，以某大型展馆X展厅为测试数据，基于整体最小二乘法对点云数据进行线性拟合，采用拟合优度及显著性检验对拟合成果的可靠性进行校核，结果展示出良好的拟合效果。随后以Geomagic Control软件作为比对平台，通过最佳拟合、3D比较、2D比较等流程，形成专业的定制报告，上述形成一套完整的点云线性拟合及比对方法，为今后类似的项目提供参考借鉴。

Abstract: In order to solve the lack of vector transformation and comparison of point cloud data in the field of architectural surveying and mapping, Hall X of a large exhibition hall was taken as test data, and linear fitting of point cloud data was carried out based on the whole least square method, and the reliability of the pseudo-composite was checked by goodness of fit and significance test. The results showed a good fitting effect. Then, Geomagic Control software is used as the comparison platform to form a professional customized report through the best fitting, 3D comparison, 2D comparison and other processes, forming a complete set of point cloud linear fitting and comparison methods, which can provide references for similar projects in the future.

1. 引言

三维激光扫描技术是近年来兴起的新型测绘技术，它通过高速激光扫描测量的方法，大面积、高分辨率地快速获取被测对象表面的三维坐标数据，实现了传统单点测量进化到面测量的技术突破，这些海量的空间点位坐标称为点云数据，该技术目前已经在各个领域进行了尝试、应用和探索，并在一些重大工程项目中起到关键性作用。

在建筑工程领域，点云数据转换为建筑图纸，包括平面、立面、剖面、总平面、细节大样等已经得到广泛推广，并成为现状测绘工作的重要技术支撑 [1] 。就目前矢量转化的手段和方式而言，大都采用将点云数据的一个面通过插件导入CAD软件中进行描绘，考虑到建筑物本身存在的不平整度、倾斜度和建成时已有的施工误差，即使人工描绘后产生细微误差，也会通过后期的统一调整进行“中和”，但在一些需要进行校对的工况下，描绘的方式显然不够严谨，需要有一个统一的、科学的矢量转换方法，以此为后续的校核比对工作提供可靠依据。

本文将以整体最小二乘法为线性拟合的计算方法，引入统计学的拟合优度及显著性检验对拟合成果进行校核，提出以Geomagic Control软件作为比对平台，通过某大型展馆X展厅的实测数据，论证上述成套拟合及比对方法的可行性，为后续的技术应用提供参考和借鉴。

2. 整体最小二乘法

整体最小二乘法是一种较为先进的最小二乘法结构，考虑线性方程组Ax = b，最小二乘法只考虑误差来自b，但是实际上误差也有可能来自A，整体最小二乘法在这一点上进行了优化考虑。目前整体最小二乘法已经广泛应用于信号处理、自动控制、系统科学、统计学、物理学、经济学、生物学和医学等多个领域中。

令A₀和b₀分别代表不可观测的无误差数据矩阵和无误差数据向量，实际观测的数据矩阵和数据向量分别为 $A=A_0+E$ ， $b=b_0+e$ 。其中，E和e分别表示误差数据矩阵和误差数据向量。整体最小二乘法的基本思想是：不仅用校正向量Δb去干扰数据向量b，同时用校正矩阵ΔA去干扰数据矩阵A，以便对A和b二者内存在的误差或噪声进行联合补偿。

$\begin{array}{l}b+\Delta b=b_0+e+\Delta b\to b_0\\ A+\Delta A=A_0+E+\Delta A\to A_0\end{array}$

以抑制观测误差或噪声对矩阵方程求解的影响，从而实现有误差的矩阵方程求解向精确矩阵方程求解的转换：

$\left(A+\Delta A\right)X=b+\Delta b\Rightarrow A_{0}X\Rightarrow b_0$

目标期望校正数据矩阵和校正数据向量都尽可能小，因此总体最小二乘问题可以用约束优化问题表述为：

$\text{TLS}:\begin{array}{l}\underset{\Delta A,\Delta b,X}{\min }{\Vert \Delta A\Vert }_F^2+{\Vert \Delta b\Vert }_2^2\hfill \\ \text{subject}\text{to}\left(A+\Delta A\right)X=b=\Delta b\hfill \end{array}$

其中F表示Frobineous范数。

整体最小二乘法的求解过程主要为：根据线性数据首先列出n × m的矩阵，构建该矩阵的增广矩阵A，对矩阵A进行QR分解(将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R)得到一个新的矩阵B，随后对矩阵B进行奇异值分解(将一个比较复杂的矩阵用三个子矩阵相乘来表示，即特征向量)，分解实则是一个提取特征值的过程，以此得到直线待定系数的整体最小二乘解 [2] 。

3. 拟合成果检验

3.1. 拟合优度

拟合优度用来描述模型与实际数据之间的误差，它可以用来反映一个模型的优劣，当某一模型的拟合优度高时，它表明该模型可能在大多数情况下是符合实际的。拟合优度可用判定系数R²表示，R²反映回归直线的拟合程度，取值范围在[0, 1]之间，R²→1，说明回归线拟合程度越好；R²→0，说明回归线拟合程度越差。拟合优度的公式为：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-\bar{y}\right)}^2}={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left({\hat{y}}_i-\bar{y}\right)}^2}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-\hat{y}\right)}^2}$

对应： $\text{TSS}=\text{ESS}+\text{RSS}$

$R^2=\frac{\text{ESS}}{\text{TSS}}=\frac{\text{TSS}-\text{RSS}}{\text{TSS}}=1-\frac{\text{RSS}}{\text{TSS}}$

其中总平方和(TSS)反映因变量的n个观察值与其均值的总离差，且可以分成回归平方和(ESS)和残差平方和(RSS)两部分，回归平方和(ESS)反映自变量x变化对因变量y取值变化的影响，残差平方和(RSS)则表示随机误差的效应。

拟合优度本质上是描述性的刻画，不涉及到对解释变量和被解释变量的总体关系的推断。对于不同的模型，不同的学科有着不同的惯性和标准，例如，在社会学中拟合优度差不多在0.3左右都是普遍的，对于时间序列拟合优度可以达到0.9以上，对于结构形状拟合优度则多在0.5左右，拟合优度不是普遍接近1的，太高的拟合优度反而会产生质疑，因此不能单纯的以拟合优度作为判断模型好坏的唯一标准。

3.2. 显著性检验

显著性检验就是事先对总体的参数或总体分布形式做出一个假设，然后利用样本信息来判断这个假设是否合理，即判断总体的真实情况与原假设是否显著地有差异。显著性检验的原理就是“小概率事件实际不可能性原理”来接受或否定假设。

显著性检验的步骤为：

1) 提出假设：H0：b1 = 0线性关系不显著；H1：b1 ¹ 0 线性关系显著。

2) 计算检验统计量F：

$F=\frac{\text{SSR}/1}{\text{SSE}/n-2}=\frac{\text{MSR}}{\text{MSE}}~F\left(1,n-2\right)$

回归均方(MSR)：回归平方和SSR除以相应的自由度(自变量的个数k)。

残差均方(MSE)：残差平方和SSE除以相应的自由度(n – k − 1)。

将回归均方(MSR)同残差均方(MSE)加以比较，应用F检验来分析二者之间的差别是否显著。

3) 确定显著性水平a，并根据分子自由度1和分母自由度n − 2找出临界值Fa。

4) 作出决策：若F > Fa，拒绝H0，线性关系显著；若F < Fa，不能拒绝H0。

4. 比对平台选用

Geomagic Control是一款逆向工程对比分析平台，它结合一系列广泛的计量工具与科学的质检工作流程，用于实现三维检测领域的简单操作与直观全方位的质量控制，该软件在短时间内，即可实现三维扫描数据与原始数模之间进行比对检测分析、最佳拟合对齐、3D比对、颜色色谱注释、2D尺寸、GD&T和出具报告等，其快速、精确、信息丰富的报告和分析为三维检测提供强大的技术支撑 [3] 。

目前Geomagic Control主要应用在制造业的检测领域，主要应用点为：① 识别并解决制造与装配问题；② 消除成本高昂的报废和返工；③ 准确一致地评估损坏、变形或磨损；④ 在零件出现故障之前做出预测；⑤ 减少质量控制瓶颈等。考虑到该软件能够处理工业级别的零件偏差，因此其处理精度完全可以满足在建筑领域的比对使用，Geomagic Control的主要比对流程见图1所示。

Figure 1. Main comparison process

图1. 主要比对流程

5. 实例测试

房屋的建筑平面测绘及复核工作越来越多的出现在既有建筑检测、改造，新建建筑施工误差比对的领域中，并成为其中举足轻重的一环，传统的测绘方式如测距仪、全站仪，由于测量精度不够、布站环境受限、数据不够直观、测绘效率较低等原因无法满足建筑测绘成果的需要。采用三维激光扫描技术可以高效的采集高精度的三维点云，基于影像级的数据可以为测绘成果转换提供有力的技术支撑，但在后处理过程中，往往采用插件导入CAD进行人工描绘，这样的矢量转换方式显得不够严谨，同时导致了精度的损失。本次将以X展厅作为测试数据，采用整体最小二乘法进行线性拟合，实现可靠的点云数据矢量转换，从而完成与原设计尺寸的比对校核工作。

5.1. 数据处理

首先将X展厅单测站点云数据调取出来 [4] ，见图2所示，进行初步的去噪处理，将坐标系转正，随后在目标上选择合适的切点设置一个参考面，将参考面网格打开进行剖切，剖切厚度设置为1 mm，见图3所示，此时目标的矢量轮廓已经清晰可见，对四条边分别进行顺时针编号(L1~L4)，并分别截取出来，将所有的直线导出为坐标合集的txt文件，并基于此进行下一步的拟合计算工作。

Figure 2. Hall X point cloud model

图2. X展厅点云模型

Figure 3. Point cloud plane cutting

图3. 点云平面剖切

5.2. 拟合计算

点云数据的量级往往在几千至几十万，甚至上百万不等，再结合不同算法的转换会形成巨大的计算量。java则具有良好的性能表现，可以高效处理大规模的数据和复杂的计算，因此依托java平台，基于最小二乘法、整体最小二乘法的原理和计算思路，以实现点云数据的矢量转换为目的，编制拟合计算软件，软件的功能模块见图4所示。针对展馆轮廓特点，本次主要采用模块4——基于整体最小二乘法的点云直线拟合计算模块进行计算。

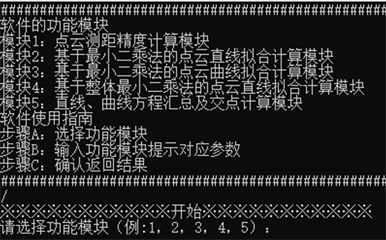
Figure 4. Point cloud linear fitting software function module

图4. 点云线性拟合软件功能模块

将截取的直线点云数据(txt)一一导入软件中，Z坐标自动删除，通过拟合计算得到各直线方程，随后选择软件中的模块5——直线、曲线方程汇总及交点计算模块，该模块可以调用上述线性拟合模块计算出的线性方程结果，通过自主选择，两两联立方程组求得交点坐标，输入CAD后完成平面轮廓线的绘制。L1线性拟合过程见图5所示，软件线性拟合计算结果详见表1。

Figure 5. L1 linear fitting process

图5. L1线性拟合过程示意

Table 1. Summary of case linear fitting calculation results

表1. 案例线性拟合计算结果汇总

5.3. 成果检验

将拟合平面成果重新导入CAD中，通过插件打开点云数据，首先可以看出前后两者基本重合一致，见图6所示，随后进入统计学的检验环节。

Figure 6. Planar pseudo synthesis is matched with point cloud

图6. 平面拟合成果与点云匹配

拟合优度：根据原始点云坐标和拟合的线性方程，分别计算每一条直线的总平方和(TSS)、回归平方和(ESS)、残差平方和(RSS)，通过拟合优度公式得到判定系数R²。

显著性检验：提出假设，H0：β1 = 0两个变量的线性关系不显著，H1：β1 ≠ 0两个变量的线性关系显著；通过检验统计量公式得到F，确定显著性水平a = 0.05，并根据分子自由度1和分母自由度n − 2查表找出对应临界值Fa。成果检验计算结果详见表2。

Table 2. Summary of results test calculation results

表2. 成果检验计算结果汇总

计算结果表明：在点云数据的矢量转换过程中，分别有61.3% (L1)、51.3% (L2)、50.4% (L3)、65.1% (L4)可以由点云数据与拟合直线的线性关系来解释，或者说，在点云数据的线性化过程中，有上述百分比是由拟合直线所决定的；此外，直线L1~L4的检验统计量F均远大于临界值Fɑ，因此拒绝H0的假设，认为线性关系高度显著。

5.4. 模型比对

分别以设计图尺寸和点云拟合轮廓建立展馆的STL模型，一起导入Geomagic Control软件中，设置一个模型为参考数据，另一个模型为测试数据，通过软件的最佳拟合对齐功能将参考数据与测试数据精确对齐，在使用中先勾选检查对称性、高精度拟合选项，再勾选只进行微调和自动消除偏差，后者可以反复应用几次，检查对齐的效果后进入比对环节。此外，对齐中如最佳拟合后还是不能有效匹配则根据形状特征改用N点、特征及RPS对齐功能进行拟合。

将两个模型首先进行3D比较，见图7所示，通过统计计算得出：展馆拟合和设计尺寸三维模型的偏差最大距离正值为104.8926 mm，偏差最大距离负值为-105.7135 mm，偏差平均距离为17.9955 mm，标准偏差为94.3829 mm，RMS估计值为96.0832 mm。在2D比较，即平面比对中，通过统计计算得出：展馆拟合轮廓和设计尺寸的偏差最大距离正值为13.7672 mm，偏差最大距离负值为−22.7566 mm，偏差平均距离为−4.4974 mm，标准偏差为14.1090 mm。随后可以通过2D注释把任意需要关注位置的偏差单独标注出来，供具体分析使用，见图8所示。

Figure 7. Model 3D comparison

图7. 模型3D比较

Figure 8. Model 2D comparison notes

图8. 模型2D比较注释

在完成所有要素分析和比对的工作后，可以使用软件的创建报告功能，导出报告支持各种类型的格式。在模板方面，报告可以根据需要进行设计和定制，包括定义报告的信息内容、模板样式、图表类型等等；在内容方面，报告会全面展示比对模型的多角度视图，除汇总上述3D、2D比较的统计数据外，还会更详细的体现偏差的百分比和分布等等。

6. 结论

1) 针对点云数据在建筑测绘中无科学矢量转换方式的现状，介绍了整体最小二乘法在线性拟合的原理和计算步骤，并引入统计学中的拟合优度和显著性检验加以复核。以某大型展馆中X展厅的点云为测试数据，基于上述理论进行计算和检验，结果表明成果具有较好的拟合效果，可为后续的比对工作提供支撑。

2) 提出以Geomagic Control软件为比对平台，将线性拟合后的平面轮廓与设计尺寸进行最佳拟合对齐、3D比较、2D比较等流程，实现全面及可靠的校核比对工作，基于软件的创建报告功能，可定制一套专业的交付报告模板。