解析几何驱动景观设计方法更新——以常州刘巷村公园景观设计为例

Updating Landscape Design Methods Driven by Analytic Geometry—Taking Park Landscape Design in Liuxiang Village, Changzhou as an Example

摘要: 当下景观规划中取点走线多用偏向定性的决策方式，许多时候会出现空间合理性有待商榷的情况，本文选取常州刘巷村的公园景观为场地，希望探索一种新的定量研究方法。在契合当地产业文化、居民需求的基础上，将解析几何应用到布局模型设计中，以对空间的分析与规划为纽带，探索解析几何与景观设计过程之间的内在逻辑。具体方法为在设计过程中对场地平面或空间合理建立坐标系，利用函数模型将空间关系转换成数字计算关系，以求合理的空间布局搭配。

Abstract: At present, as the deciding way of drawing lines and points in landscape planning is more of the tendency to qualitative methods, sometimes the arrangement of space is not that reasonable. In this paper, the park landscape in Liuxiang village, Changzhou is taken as the site selection and a brand-new quantitative research method is hoped to be explored. On basis of fitting the local agricultural culture and the needs of habitants, we resort to analytic geometry in the design of layout model. The analysis and arrangement of space are able to be seen as the links between analytic geometry and landscape design, so that the inner logic can be researched. When it comes to the concrete measures, rational coordinate systems are to be established in the plan or space of the site. Only in this way can the spatial relationship be transformed into digital relationship by functional model, thus to rationalize spatial distribution.

1. 研究理论与背景

当代随着计算机技术、数字化技术的不断发展，基于数据的研究已经渗透到各行各业，那么在设计领域亦是如此，这对于习惯于基于事件定性分析的景观设计者们来说，已然成为了一项挑战。解析几何是数学领域数形结合的重要代表，探索其在景观设计中发挥作用的可能性与路径，是推动设计行业多元化发展的重要动力。

(一) 解析几何和景观设计的内在联系

解析几何是一门数学学科，它研究的是点、线、面等几何元素的性质和关系。在景观规划和设计中，可以抓住“图形”这一共通点，通过解析几何的方法将数学原理合理运用在设计方案的生成过程中。如此，可以分析和描述景观空间的形态、结构和特征，从而帮助设计师更好地理解和规划景观空间。核心点是把设计者在场地中的设计意向转化到基于坐标系的图像系统中，通过对图形、函数的计算构造出两个学科之间的运作关系，从而使有效的数据成为构成设计的关键元素。

(二) 解析几何在景观设计中的实用意义

解析几何在景观规划和设计中具有重要的概念和意义，可以帮助设计师更好地理解、分析和表现景观空间，从而创造出更美丽、实用、符合人类需求的公共空间。

1、形态分析

解析几何可以帮助设计师分析和描述景观空间的形态特征，如平面形状、曲率、几何形式等，从而有助于设计师制定合适的设计方案。几何图形甚至可以直接运用在设计中，这其中的方圆曲直各依其所，优美的弧线给人以优雅之美的直观感受，它们是数学立体图形用于景观设计中的重要美学实例。使得设计成果显得或典雅，或对称，或美观，既是对传统的继承与发扬，也体现着一种新颖的设计思路。

2、空间组织

解析几何可以帮助设计师理解景观空间的组织原理和规律，如空间分割、空间层次、空间关系等，从而有助于设计师合理规划和布局景观空间。我们应用几何学的基础知识，计算图形本身的多种要素或者物与物之间的空间关系，可以从定量的角度更为理性地确定景观中各个对象较为合理的所处之地，从而获得空间布局上的最优解 [1] 。

3、技术应用

解析几何可以被应用于景观设计的技术方面，如CAD制图、三维建模、地形分析等，从而帮助设计师更加高效、精确地完成设计任务。再加上对场地中各设计元素的空间关系、自身特征等都有着基于具体数值的了解下，考虑施工材料的密度价格，就能清楚计算出所需的材料之多少以及总体所需之金额，并加以控制，从而工程预算的出具便有了切实可查的依据。

(三) 解析几何在景观设计中的应用示例

这里我们拿2019年江苏省扬州中学月考试题为例：

某人工湖畔有两条相互垂直的直线公路，这里设为l₁与l₂，这两条路的交点设为O。为了游客游玩之便利，需要修建一条公路与人工湖相连的直线路径AB。人工湖的轮廓可近似看成一个圆心为O′，半径为2百米的圆，且公路AB与圆O′相切，圆心O′和l₁、l₂之间的距离均为5百米，设∠OAB = θ，AB长为L (单位：百米)。则若需要新修的路径最短，当如何处置？

Figure 1. Result of establishing the coordinate system of the question

图1. 题干建系结果

首先当以O为原点，直线l₁和l₂分别为横纵两轴建立平面直角坐标系，建系结果见图1，从而建立L关于θ的函数解析式：

∵ $\text{OA}=L\cos \theta$ ， $\text{OB}=L\sin \theta$

∴直线AB的方程为 $\frac{x}{L\cos \theta }+\frac{y}{L\sin \theta }=1$ ，及 $x\sin \theta +y\cos \theta -L\sin \theta \cos \theta =0$

点O′的坐标为(5,5)，直线AB与⊙O′相切，则 $\frac{\left|5\sin \theta +5\cos \theta -L\sin \theta \cos \theta \right|}{\sqrt{{\sin }^2\theta +{\cos }^2\theta }}=2$ ，O′在直线AB的上方，结合实际意义，则有：

$L=\frac{5\left(\sin \theta +\cos \theta \right)-2}{\sin \theta \cos \theta }$ , $\theta \in \left(0,\frac{\pi }{2}\right)$

问题就转化为求定义域内L的最小值。可设 $t=\cos \theta +\sin \theta$ ，则有 $f\left(t\right)=2\cdot \frac{5t-2}{t^2-1}$ ， $t\in \left(1,\sqrt{2}\right]$ 。

求导 $f^{\prime }\left(t\right)=\frac{-2\left(5t^2-4t+5\right)}{{\left(t^2-1\right)}^2}$ ， $t\in \left(1,\sqrt{2}\right]$ ，其在定义域内恒小于0，则函数f(t)在定义域内单调减，所以当 $t=\sqrt{2}$ 及 $\theta =\frac{\pi }{4}$ 时， $L_{\min }=10\sqrt{2}-4$ ，由此所需方案就被精准解析出来了。

2. 刘巷村公园景观设计

(一) 项目背景

全面建设社会主义现代化国家，最终实现中华民族之伟大复兴，是一个任重道远的过程 [2] ，党的二十大报告指出，“要全面推进乡村振兴，坚持农村优先发展，扎实推进乡村产业、人才、文化、生态、组织振兴”。

那么对于刘巷村的整体规划，是意在打造和强化一个现代产业化农业区，要扣准“现代化”这一基本原则，打造具有一定特色的公共建筑与景观形态，与其他传统江南水乡的整体风貌做出区别，就是说，与其打造一个现代人司空见惯的古镇，把所谓的“乡愁”强加于这里的人们，倒不如利用好当地现有的特色与优势，结合今人所掌握的智慧与技术，去建设一个更容易为当下的人们所接受和栖息的场所。

(二) 公园选址场地分析

1、刘巷村分析

刘巷村坐落于常州市钟楼区，东临扁担河，南靠卜弋村，西接琵琶村村委会，北边为奔牛镇新墅村。村内粉墙参差，农场纷然，阡陌交通，道路整洁，还有农产品科普展示中心，以推广刘巷村的产业特色。此处空气和环境良好怡人，也被称为“花园里的村庄”。刘巷村还修建了“微花园”等一系列微环境改造，以便游客和村民游览休憩。

刘巷村有着水芹和翠冠梨两大极富特色的产业优势，水芹尤盛。村中建立了“合作社 + 基地 + 农户”这一较为完整的产业链，促进生态与产业融合，1978年，国家要求引入家庭联产承包责任制，农民有权耕种自己的土地，村民们就开始大量种植水芹菜，如今，刘巷村已因此被称为“水芹之乡”，在设计改造的过程中，我们可以通过建筑、景观的新颖特色表达，来产生话题热点，从而提升“刘巷村水芹”知名度就是自然而言的事情了。良好的人居环境，生态环境，配上有机、生态的农产品，方能使刘巷村焕发新生。

2、场地存在的问题

刘巷村在产业缺少更有效的宣传策略。当搜索刘巷村关键词时，在各大知名网站的信息过少，而用户往往习惯先去搜索资料再选择是否出行或购买产产品。刘巷村的资料不够统一，用户不得不各个软件查找并自己整合在一起，容易导致用户中途放弃的现象。在自媒体、网络直播盛行的时代，用户没办法通过常见方式了解刘巷村或购买刘巷村的特产。如在短视频平台抖音上，通过镜头的方式讲述乡村发展历程，并总结出完整的旅游攻略和购买攻略，或在固定时间直播带货发展乡村经济，用户便可更直观的了解刘巷村 [3] 。

其次缺少对刘巷村完整的系统设计。结合环境设计、乡村规划、视觉传达、数字媒体等设计方向做出一整套完整的乡村系统设计。如乡村品牌的IP形象、创意的产品包装、线上的交互体验等设计打造乡村形象，使数字化设计与乡村真正融合。

3、公园选址

本次公园场地的选址见图2，位于人员聚居区域中心偏东部，南北人家，西接空地，东有良田，在村中有着较为便利的交通条件与区位条件。基于以上条件，先对场地整体布局进行了基于现状的定性规划，从而从根本上达到适配村中人员来往路径与感官体验的目的。

(三) 解析几何在景观平面中的应用

首先从刘巷村特色水芹产业文化入手。水芹叶柄为中空结构,有较大的髓腔，有9处叶柄厚角组织，由此进行空间的几何重构，确定公园主次入口的分布见图3。

如此，在场地东面的池塘处寻找到篮球场出口最近的点以确定一个临水观景台的位置见图4，使得

Figure 2. Site selection of park sites

图2. 公园场地的选址

图3. 公园总体空间结构生成过程

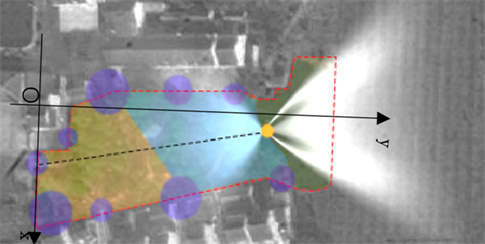
Figure 4. Determine the location of a waterfront observation deck

图4. 确定一个临水观景台的位置

在观景台上能够更清楚得获得村庄人居环境的视野，站在台上极目远眺，东可望田园万顷，西可观烟火人家。为了确定观景台的准确位置，这里在所需范围内以南北向为x轴，东西向为y轴建立平面直角坐标系，通过卫星定位近似确定池塘岸线所呈现的函数图像关系见图5，开始节点位置的计算。

篮球场处出入口的位置为(20,0)，则近似可求点(20,0)到函数 $f\left(x\right)=\frac{1}{10}{x}^2+90$ ( $x\in \left[0,10\right]$ )图像上的点距离最近的点：

5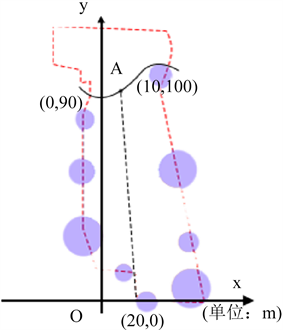

图5. 观景台函数图像关系

设观景台位置点A为 $\left(a,\frac{1}{10}{a}^2+90\right)$ ，点A到出口长度为L，则有：

$L=\sqrt{{\left(a-20\right)}^2+{\left(\frac{1}{10}{a}^2+90\right)}^2}$ ， $a\in \left[0,10\right]$ 为了便于计算，对L平方处理后定义函数：

$u\left(a\right)=\frac{1}{100}{a}^4+19a^2+8500$ ， $a\in \left[0,10\right]$ 。求导得 $u^{\prime }\left(a\right)=\frac{1}{25}{a}^3+38a$ ( $a\in \left[0,10\right]$ )，这个导函数在定义域[0,10]内恒大于0，所以u(a)是单调增函数，此时可以得知当a = 0时，函数u(a)(相当于距离L)可以取得最小值。由是确定了观景台的位置，量化完成了这一节点的规划过程。

(四) 解析几何在景观空间中的应用

空间解析几何在景观设计中也能发挥非常直观有效的辅助作用，如为了某些视觉目的，需要确定某些路径、台面的外形走向。如上文的观景台与下方水面的垂直距离为3米，测得取点处和水上建筑的东

南角的连线和水面的夹角为α，tanα的值为 $\frac{3}{5}$ ，现在还需要紧贴水做一步道，要求人走在步道上时望向

观景台取点处的视线和前述连线的夹角恒为30˚，那么如何确定人行走的轨迹或者这个步道的形状就需要用到空间解析几何的知识。

根据上文描述，我们可以将这些点线面关系简化为下见图6：

将取点处设为点A，建筑东南角设为点B，构成步道的动点设为点P，以点A到水平面的垂足为原点O，OB为y轴，垂直于OB于点O的直线为x轴，直线OA为z轴，建立空间直角坐标系见图7，这样就可以在这个坐标系中求得点P的运动轨迹，过程如下：

点A的坐标为(0, 0, 3)，点B的坐标为(0, 5, 0)，可设点P的坐标为(x, y, 0)

则 $AB=\left(0,5,-3\right)$ ， $AP=\left(x,y,-3\right)$ ，所以可以构成方程 $\text{cos}\left(AB,AP\right)=\frac{5y+9}{\sqrt{34}\times \sqrt{x^2+y^2+9}}=\frac{\sqrt{3}}{2}$ ，经过对这个式子的变形整理，可以得到 $51x^2+{\left(y-90\right)}^2=7903$ ，显然这是一个椭圆，则点P就在这个圆锥曲线上运动而构成步道的形态就可以了。

(五) 解析几何在施工上的应用

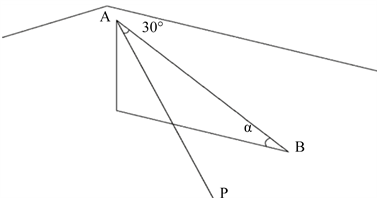
Figure 6. Simplification of point, line, and Surface of people- road relationship

图6. 人–路关系点线面简化

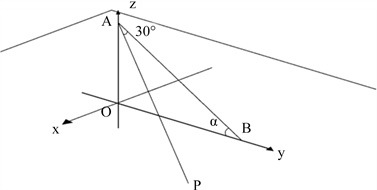
Figure 7. Spatial coordinate system of people-road relationship

图7. 人–路关系空间坐标系

在景观建设的施工过程中，常常会遇到土方填挖的问题，这也是施工成本的重要组成部分。这里将以此公园的土方问题为例，浅析解析几何的方法对施工成本控制的积极作用。

公园东部有一池塘，连通刘巷村东边的扁担河，为了节约水资源以更好地支持村中的水芹产业，决定将原本的近似于二次函数图像的弧形水渠，它深0.5米，宽1米，现在改为等腰梯形见图8，这其中就涉及填土的问题，如何使填土最少，由于长度的恒定，需要计算的就是截面面积的变化。我们将其截面底部顶点作为原点。建立平面直角坐标系。

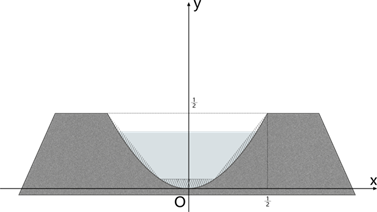
Figure 8. Coordinate representation of canal cross-section

图8. 水渠截面坐标表示

易得原水渠所示的函数关系为：

$y=2x^2\left(x\in \left[-\frac{1}{2},\frac{1}{2}\right]\right)$

设点M的坐标为(t, 2t²) ( $0<t<\frac{1}{2}$ )，则梯形面积：

$S\left(t\right)=\frac{1}{2}\left(2t+1\right)\left(\frac{1}{2}-2t^2\right)=-4t^3-2t^2+t+\frac{1}{2}$ , $t\in \left(0,\frac{1}{2}\right)$

求导得 $S^{\prime }\left(t\right)=-12t^2-4t+1$ , $t\in \left(0,\frac{1}{2}\right)$

令 $S^{\prime }\left(t\right)=0$ ，得在定义域上到 $t=\frac{1}{6}$ ，列表得：

所以，当等腰梯形底边长 $\frac{1}{3}$ 米时，这个梯形的截面面积最大，既符合改为梯形的功能需求，原水渠中需要回填的土方量也是最少的，也就达到了节水效果 [4] 。

(六) 设计方案

以上的两个节点设计是在本设计中利用解析几何原理解决实际设计问题的代表性示例，在这个公园设计中，大到空中栈道，小至室外景观座椅的外形生成，都或多或少地蕴含着几何图形之间相互作用、相互成就的巧妙关系，当然，景观设计最终还是要回归到人的直观体验本身，不可在函数模型上做过多的纠缠而让人感到本末倒置。

以下是本次公园设计总平面图与细节表现见图9。

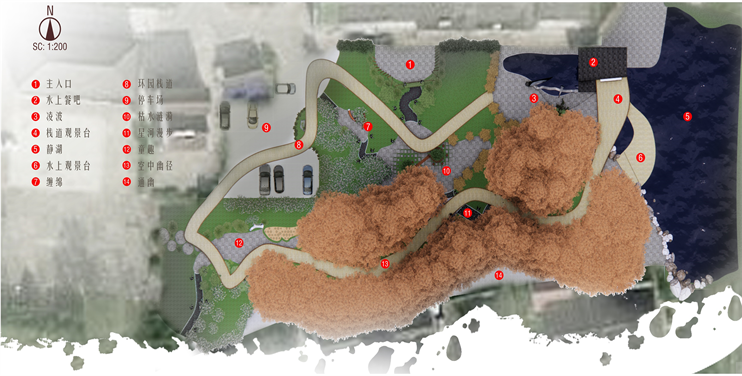
Figure 9. Park design master plan and detail representation

图9. 公园设计总平面图与细节表现

1、依然是从水景说起，以建筑作为两岸的连结，是江南独特的景致，这里将这样的空间又进行了丰富，上下两层的设置见图10使得游人在观景时有了更多的体验与选择见图11。

2、结合水芹叶与根茎的形象特点设计了路灯的造型见图12。

3、利用弧线构成的水上的座椅，供人休息的同时也增强了空间的艺术感与灵动性见图13。

4、在景观轴线的交叉处、场地的中心位置着力打造，设计了绕树的桌椅以及渐变的铺装见图14，兼顾了景观的生态性、艺术性、创新性。

5、栈道架于空中而部分丛林掩道见图15，可让人在一时的满目枝桠间忘记自己与泥土分离，走过树林后，豁然开朗而顿生豪迈之感。

Figure 10. Spatial analysis of viewing platform

图10. 观景台空间分析

Figure 11. The rendering of viewing platform

图11. 观景台效果图

Figure 12. Renderings of streetlights

图12. 路灯效果图

Figure 13. The rendering of viewing platform

图13. 水上座椅效果图

Figure 14. Table and chair renderings

图14. 桌椅效果图

Figure 15. Forest walkway Renderings

图15. 林中步道效果图

3. 解析几何在景观中的局限性与未来发展

(一) 局限性

解析几何在空间理论和分析方法上是基于数学分析的，在景观空间设计中存在一些局限性，如下所述：

1、偏向于理论分析：解析几何是一种理性分析方法，更偏向于对空间形式、结构和组合进行理性分析和优化，而对于景观空间中的感性和主观因素，如情感、文化和历史背景等，解析几何并不能很好地进行处理。

2、忽略了自然因素：景观空间设计通常需要考虑到自然因素，如地形、水文和生态等。然而，解析几何主要关注于空间形式和组合，对于这些自然因素的分析和处理相对较少。

3、依赖于规则几何：解析几何常常依赖于规则几何，如直线、圆形和椭圆等，而对于景观空间中复杂的景观空间，解析几何的应用会受到一定的限制。

因此，在景观空间设计中，解析几何不能单独应用，需要结合实际情况和其他分析方法进行综合分析和设计 [5] 。

(二) 未来发展方向

1、整合主观因素：未来景观设计里的解析几何方法需要更好地整合场地所在之处的人文特征与人的主观感受等感性因素，以更好地满足用户需求和设计目标。

2、结合数字技术：对于复杂的景观空间，解析几何的方法需要结合数字技术，如虚拟现实、增强现实和人工智能等，以提高设计效率和精度，并为用户提供更好的交互体验。

3、强化自然因素：未来的解析几何方法需要更好地强化自然因素的分析和处理，如地形、水文和生态等，推导出目标函数关系更为合理的定义域，以更好地实现景观空间的生态可持续性和生态环境效益。

4、自由处理能力：未来的解析几何方法需要更好地发展非规则几何的处理能力，如曲线和自由曲面等，以更好地满足景观空间中的自然属性形态的设计需求。

4. 结语

基于解析几何的景观设计在布局时布局搭配合理的模型，首先根据设计内容自身的空间特征，确定设计时所需要的坐标系以及相对应的函数或曲线关系，通过准确的计算得出设计方案的骨架。在这样的基础上，构建所要设计的景观布局，实现对景观空间规划的定量分析。这次尝试表明，这种方法设计出的方案比传统定性分析得出的方案合理性要高，更能够满足可持续发展的要求。回归到景观设计的表现上，则更加能够有的放矢，让景观设计脱离重艺术而缺技术的窘境。

注释

文中所有图片均为作者自绘。