基于系统动力学的机场出租车载客决策分析——以虹桥机场为例

Analysis of Airport Taxi Passenger Carrying Decision Based on System Dynamics—Taking Hongqiao Airport as an Example

摘要: 随着人口流动的日益频繁，机场的工作压力也日益增加，如何对出租车和乘客进行合理分配成为问题。针对不同的主客观因素，出租车司机往往会面对排队载客与空车回市区的选择。本文首先利用系统动力学模型建立机场出租车载客系统动力学模型，对五个影响出租车司机决策的因素进行分析与计算，并通过上海虹桥机场旅客吞吐量、飞机起落架次等仿真模拟来对出租车司机决策进行策略分析。然后，我们利用分类讨论思想及优先级调度算法对出租车司机“优先权”标准进行定义，分析出两种排队方法，以保证短途返回载客的出租车司机收益与长途返回载客的出租车司机收益尽量均衡。

Abstract: With the increasing frequency of population mobility, the work pressure at airports is also increasing, and how to allocate taxis and passengers reasonably has become a problem. Due to different subjective and objective factors, taxi drivers often face the choice of queuing to carry passengers or returning to the city empty. This article first uses a system dynamics model to establish a system dynamics model for airport taxi passenger transportation, analyzes and calculates five factors that affect taxi driver decision-making, and conducts strategic analysis of taxi driver decision-making through simulation of passenger throughput and aircraft takeoff and landing sorties at Shanghai Hongqiao Airport. Then, we use the concept of classification discussion and priority scheduling algorithms to define the “priority” standard for taxi drivers, and analyze two queuing methods to ensure that the income of taxi drivers returning for short distance passengers is as balanced as possible with that of taxi drivers returning for long distance passengers.

1. 引言

随着现代科技的发展与时代的进步，出行、旅游人数也以较快的增速增长。机场经常是人满为患，大多数乘客下飞机后要去市区(或周边)的目的地，出租车成了机场出行的一大重要交通工具。如何在机场快速乘坐到出租车也成了一大难题。为了高效地配置出租车和乘客，我们需要分析出租车行为并用优良的系统来管理。

在确定的某一时间段内抵达的航班数量与乘客数量以及在排队等候的出租车数量是司机可以观测到的，即确定信息。通常司机决定是否载客或直接返回市区与其个人的经验判断有高度相关性，比如季节因素、时间因素、航班数量、乘客数量以及其他私人原因都有可能影响司机的最终决策。

在我们实际生活中，还有很多其他影响出租车司机作出决策的因素。在本文的研究中，我们将结合实际情况，建立合理严谨的数学模型研究解决以下问题：

1) 分析影响出租车司机载客的因素及其相关关系，为使机场交通高效运行及出租车司机收益最大化，建立相关决策模型，并进行策略分析。

2) 以某一机场及其所在地出租车载客的相关数据为例，分析模型的有效性和相关性，列出司机的选择方案。

3) 在司机不可拒载和选择乘客，司机可多次往返载客的前提下，应给予短途载客返回机场的司机一定优先权，制定相应的制度，使得司机收益均衡。

2. 模型假设与变量说明

2.1. 模型假设

根据黎冬平等(2009) [1] 的研究，为使问题易于理解，我们作出以下合理假设：

1) 假设不存在出租车司机拒载情况；

2) 假设蓄车池内车辆按规定正常排队行驶，不存在车辆刮擦等事故导致蓄车池内车辆无法正常行驶的情况；

3) 假设蓄车池内都为正规出租车并且排队的乘客都已选择出租车交通方式，无黑车、私家车等车辆存在。

2.2. 变量说明

Table 1. Variable description table

表1. 变量说明表

本文选取天气状况、汽车数量、客流量、航班情况、其他原因5个变量，如表1为各变量说明表，以下对各变量进行解释说明。

2.2.1. 天气

1) 正常天气

在天晴、多云等良好天气状况下，天气情况往往不会对出租车司机载客与否的选择造成决定性影响；当遭遇雨雪天气时，更多司机会倾向尽快返回市区而选择直接放空返回市区接客或下班，因此会对出租车司机的载客决策有一定影响。

2) 极端天气

当有台风等极端天气来临时，天气将会对出租车司机的载客决策有决定性影响，大部分出租车司机会选择放空返回市区下班回家。

2.2.2. 出租车数量

出租车司机会根据“蓄车池”的车辆数判断待客所需花费的时间成本，从而决定是否载客回到市区。

2.2.3. 旅客数量

出租车司机会根据机场航班到达数判断可能的候客数，从而决定是否要花费时间成本载客回到市区。

2.2.4. 时间

不同季度及每天的不同时间段都会对机场的航班数、机场的开放时间有一定的影响，司机也会根据不同的时间选择是否要载客回市区。

2.2.5. 其他原因

1) 汽车状况

出租车在上客区的等待及运送乘客会消耗汽车的油量及机制，司机会根据汽车油量等车身状况选择是否等待上客及载客回市区。

2) 个人事务

如若司机因个人事务需要尽快返回市区，会对其载客选择产生一定影响。

3. 模型的建立与求解

3.1. 机场出租车载客系统动力学模型的建模步骤

机场交通问题是社会交通问题乃至经济发展问题的影响因素之一。然而在目前对交通需求逐渐增大的形势下，我国机场出租车规范以及管理制度与系统仍相对滞后，有较大改善空间。

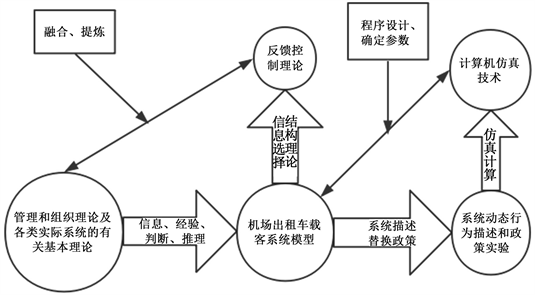
Figure 1. Composition of dynamic model for airport taxi passenger carrying system

图1. 机场出租车载客系统动力学模型的组成

Figure 2. Modeling process of dynamic model for airport taxi carrying system

图2. 机场出租车载客系统动力学模型的建模流程

并且随着社会的进步，出行、旅游人数也以较快的增速增长，机场附近交通拥堵也成为了一大问题。由于相关因素较多，且不好确定，传统的方法很难对机场出租车的管理做出全面、完善的理论分析，这导致了机场交通效率的低下。因此，我们将运用系统动力学模型以及优先级调度算法等方法对机场出租车的管理进行更为严谨的系统性的研究，并以此为根据建立相关的模型，对相关的问题进行全面分析。

机场出租车载客系统动力学模型将以管理组织理论为模型基础依据，并将其与反馈理论结合，综合得出系统的动力学模型，并根据蒙特卡洛模拟作为有力的仿真手段，使我们的模型更加便于使用，切合实际，从而帮助完善机场出租车问题的管理。

参考柳伍生(2010) [2] 以及桂寿平等(2002) [3] 研究方法，机场出租车载客系统动力学模型的组成如图1所示，相应的建模流程如图2所示。

根据系统动力学模型的建模流程，我们可以大致把系统动力学的研究过程分为以下6个步骤：问题定义、模型概念化、模型数学表达、仿真、评价及政策分析。

我们将用DYNAMO语言对模型的数学表达、仿真和政策分析这三个阶段进行模型行为分析及拟合度评价，并通过其对未来经济、社会发展的匹配程度进行相关的有效政策分析。

3.2. 机场出租车载客系统动力学模型的建立

3.2.1. 机场出租车载客系统动力学模型的因果关系分析

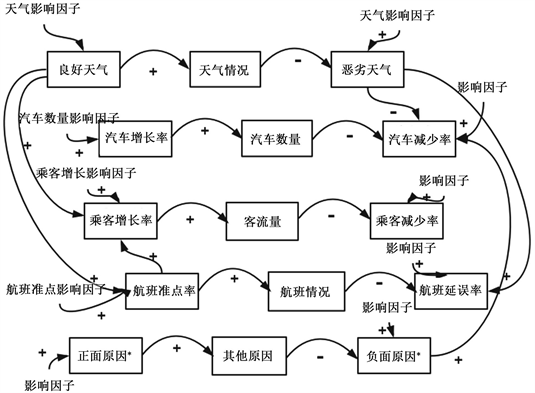
Figure 3. The basic causal relationship of the dynamic model of airport taxi passenger carrying system

图3. 机场出租车载客系统动力学模型的基本因果关系

通过对机场出租车载客系统的深度剖析，我们得到了如图3和4所示的基本因果关系图和基本反馈环。

由因果关系图可知，如果天气情况恶劣，将使飞机延误率提高，从而导致实时机场的客流量减少；同时，天气情况的恶劣也将导致出租车数量减少。如果司机或出租车本身发生其他原因(如油量不够、家中事务等)，也会导致机场“蓄车池”出租车数量减少；如果实时机场乘客数量减少，也会导致机场“蓄车池”出租车数量的减少。

Figure 4. Basic causal feedback loop

图4. 基本因果反馈环

3.2.2. 机场出租车载客系统动力学模型的建立

机场出租车载客系统动力学模型可划分为5个模块：天气情况子构造、汽车数量子构造、客流量子构造、航班情况子构造、其他原因子构造。以这5个水平变量(X₁, X₂, X₃, X₄, X₅)的反馈系统表述机场出租车载客系统。

系统向量的动态方程为：

$X_1=C_{11}{X}_1$ (1)

$X_2=C_{22}{X}_2+C_{21}{X}_1+C_{25}{X}_5$ (2)

$X_3=C_{33}{X}_3+C_{34}{X}_4$ (3)

$X_4=C_{44}{X}_4+C_{34}{X}_4$ (4)

$X_5=C_{55}{X}_5+C_{21}{X}_1+C_{25}{X}_5$ (5)

故有

$X΄=AX$ (6)

式中，X∈R^m，

$A=\left[\begin{array}{ccccc}{C}_{11}& 0& 0& 0& 0\\ C_{21}& C_{22}& 0& 0& C_{25}\\ 0& 0& C_{33}& C_{34}& 0\\ C_{41}& 0& 0& C_{44}& 0\\ 0& 0& 0& 0& C_{55}\end{array}\right]$ (7)

C₁₁为恶劣天气指数与良好天气指数之差，C₂₁为良好天气指数对汽车增长率的促进程度，C₂₂为汽车增长率与汽车减少率之差，C₂₅为其他正面原因对汽车增长率的促进程度，C₃₃为乘客增长率与乘客减少率之差，C₃₄为航班准点率对乘客增长率的促进程度，C₄₁为良好天气对航班准点率的促进程度，C₄₄为航班准点率与航班延误率之差。

由此得出，系统的状态空间表达式如(8)：

$X\text{΄}=AX=\left[\begin{array}{ccccc}{C}_{11}& 0& 0& 0& 0\\ C_{21}& C_{22}& 0& 0& C_{25}\\ 0& 0& C_{33}& C_{34}& 0\\ C_{41}& 0& 0& C_{44}& 0\\ 0& 0& 0& 0& C_{55}\end{array}\right]\left[\begin{array}{c}{X}_1\\ X_2\\ X_3\\ X4\\ X5\end{array}\right]$ (8)

式(6)为线性定常系统齐次方程。当系统的初始时刻为t₀ = 0时，初始状态为X₍₀₎，即X_(t0) = X₍₀₎

方阵A的特征方程为

$\left|\lambda I-A\right|=\left[\begin{array}{ccccc}\lambda -C11& 0& 0& 0& 0\\ -C21& \lambda & 0& 0& -C25\\ 0& 0& \lambda -C33& -C34& 0\\ -C41& 0& 0& \lambda -C44& 0\\ 0& 0& 0& 0& \lambda -C55\end{array}\right]$ (9)

式中，λ为特征方程的根，I为单位矩阵。

$A=\left[\begin{array}{ccccc}{\lambda }_1& & & & \\ & {\lambda }_2& & 0& \\ & & {\lambda }_3& & \\ & 0& & {\lambda }_4& \\ & & & & {\lambda }_5\end{array}\right]$

其中λ₁，……，λ₅为方阵A的特征根，故有

$Ф\left(t\right)=e^{A\left(t-0\right)}=T\left[\begin{array}{ccccc}{\text{e}}^{\lambda 1t}& & & & \\ & {\text{e}}^{\lambda 2t}& & 0& \\ & & {\text{e}}^{\lambda 3t}& & \\ & 0& & {\text{e}}^{\lambda 4t}& \\ & & & & {\text{e}}^{\lambda 5t}\end{array}\right]{\text{T}}^{-1}=\left[\begin{array}{ccccc}{R}_{11}& R_{12}& R_{13}& R_{14}& R_{15}\\ R_{21}& R_{22}& R_{23}& R_{24}& R_{25}\\ R_{31}& R_{32}& R_{33}& R_{34}& R_{35}\\ R_{41}& R_{42}& R_{43}& R_{44}& R_{45}\\ R_{51}& R_{52}& R_{53}& R_{54}& R_{55}\end{array}\right]$ (10)

$Ф\left(t\right)=e^{A\left(t-0\right)}$ 表示由系统初始状态引起的系统的运动。

由此得机场出租车载客系统动力学模型的解析表达式：

$X\left(t\right)=Ф\left(t\right)X\left(0\right)$ (11)

3.3. 策略分析

根据以上机场出租车载客系统动力学模型的求解，我们可知出租车司机对于载客与否的抉择主要受五个因素影响：天气状况、航班情况、“蓄车池”出租车数量、乘客数量、其他原因。

当天气状况良好时，出租车司机往往会前往到达区排队等待载客返回市区；当天气恶劣时，出租车司机更倾向于直接放空返回市区。

当航班正点到达时，出租车司机可以选择合适的航班时间前往到达区排队等待载客返回市区；当航班延误时，为了避免浪费不必要的时间成本，出租车司机往往会直接放空返回市区。

当“蓄车池”出租车数量适量且乘客数量较多时，出租车会愿意前往到达区排队等待载客返回市区；当“蓄车池”出租车数量过于饱和时，出租车会倾向直接放空返回市区。

当乘车区乘客数量较多时，出租车司机会愿意前往到达区排队等待载客返回市区；当乘车区乘客数量较少时，出租车司机往往会节省时间成本而直接放空返回市区。

当司机有其他原因(如油量不足、家中事务等)发生时，会选择直接放空返回市区。

3.4. 方案分析

3.4.1. 航班放行正常率变化仿真

航班放行正常量的仿真结果如图5所示，由仿真结果可以看出，上海虹桥机场的航班放行正常率在2006~2010年间保持在85%~90%之间，虽然航班放行正常率在此期间出现低于85%的情况，但并不影响航班放行正常率的平稳趋势。到2010年5、6月左右航班放行正常率出现了两次大幅度的下滑和一次大幅度的上浮，在第二次下滑之后，到2012年航班放行正常率有小幅度的回升，但在2012年之后航班放行正常率就持续下滑。这说明随着社会的发展，人们的安全意识也更加强烈，航班放行检查机制也更加严格，航班放行正常率也会随之有所波动。

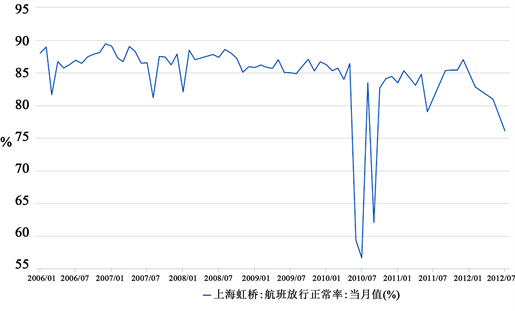
Figure 5. Normal flight release rate at shanghai Hongqiao airport from 2006 to 2012

图5. 2006~2012年上海虹桥机场航班放行正常率

3.4.2. 旅客吞吐量与飞机起降架次变化仿真

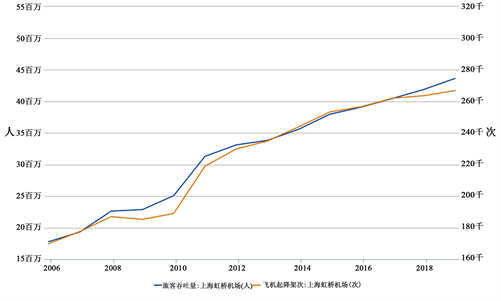
Figure 6. Passenger throughput and aircraft takeoff and landing sorties at Shanghai Hongqiao Airport from 2006 to 2018

图6. 2006~2018年上海虹桥机场旅客吞吐量及飞机起降架次

由图6可知，上海虹桥机场的旅客吞吐量日益增加，这一方面是上海虹桥机场国际交通枢纽以及基础设施的不断完善，另一方面是，上海是我国的经济金融中心，各种大型活动也会选择上海作为活动举办地，随之而来的也是不断上涨的旅客吞吐量。

由图6可知，上海虹桥机场的飞机起降架次越来越多。随着上海虹桥机场发展的要求，航班次数的增加以及航线的不断拓宽，成为了飞机起降架次增加的主要原因。并且随着上海虹桥机场旅客吞吐量的不断增大，飞机起降架次也随之增加。

根据以上仿真模拟分析，上海虹桥机场出租车司机会选择前往到达区排队等待载客返回市区。

4. “优先权”排队方法分析

4.1. 分类讨论法

该模型以上海虹桥机场为例，利用出租车收益、出租车油费、出租车行驶距离与出租车净收入等变量构造分段函数，对出租车“优先权”标准进行定义，使具有“优先权”的出租车节省时间成本，从而给出使出租车收益尽量均衡的“优先”安排方案。

首先，我们通过查找资料了解到上海地区出租车大多使用92号汽油，并搜集了其汽油价目表，如表2所示。

Table 2. Price list of different gasoline models in Beijing, Shanghai, and Jiangsu regions (RMB/Liter)

表2. 北京、上海、江苏地区不同型号汽油价目表(元/升)

同时，我们收集了上海市出租车收费标准作为参考(该模型以日间收费为例)，如表3所示。

Table 3. Shanghai taxi charging standards

表3. 上海市出租车收费标准

为计算出租车净收益，我们利用下列公式：

出租车净收益 = 出租车收益 − 出租车油耗

(出租车油耗统一为0.08升/公里)

由公式及数据可得：

$y=\{\begin{array}{c}-1.056x-140\le x\le 3\\ 1.444x+6.53＜x\le 10\\ 2.544x-5.2x＞10\end{array}$

由函数我们可以得到出租车净收益分段曲线图，如图7：

根据图中曲线变化，我们对载客返回机场的出租车分为三类：

1) 优先Ⅰ类：载客3公里以内返回机场；

2) 优先Ⅱ类：载客大于等于3公里且小于10公里返回机场；

3) 正常载客：载客大于10公里返回机场。

出租车司机根据自己所属的类别进入相应的“蓄车池”及上客区接载乘客(每个上客区乘客流量相同)，优先类出租车则可以通过减少等待时间优先接客，从而使自身收益与其他车辆尽量均衡。

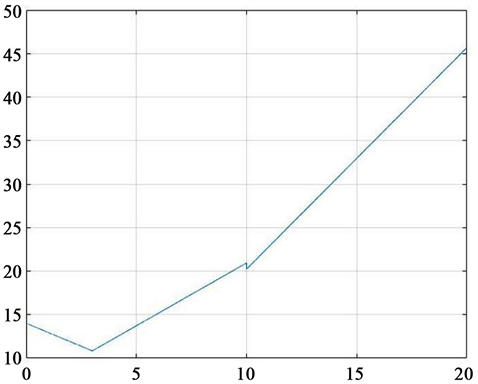
Figure 7. Taxi net income segmented function diagram

图7. 出租车净收益分段函数图

4.2. 优先级调度算法

多次短途载客的出租车司机一方面有着多次载客的机会，一方面也要承担从机场送完乘客后回机场的空载损失。为使收支相对平衡，管理部门所给的“优先权”在一定程度上是给了短途往返的出租车司机更多拉客的机会，而在机场出租车排队区拥有更多拉客的机会，就意味着有更短的等待时间。所以本题要解决的是如何让短途往返的出租车拥有更短的等待时间。

可借鉴计算机CPU (中央处理器)处理进程的方法来解决本题。将出租车的整个短途往返的过程看作一个程序，使其等待时间更短意味着整个程序优先级更高，系统要优先执行整个程序。我们从操作系统的多种调度算法中采用优先级调度算法并结合实际情况，得出解决方法。

优先级调度算法通常用于作业调度和进程调度，这里的优先级指的是在CPU等待队列中，作业运行的紧迫程度，该算法每次从作业队列中选择优先级最髙的，把它们调进内存中，分配I/O等资源，创建进程后处于就绪状态。当进程处于执行状态前，从就绪队列中选择优先级最高的进程，使其优先占用CPU，使其进入执行状态。在实际情况下，机场管理人员无法快速机动选择优先级最高(短途往返时间最短)的出租车，所以我们让选择让出租车进入等待时间最短并且队列最短的出租车排队队列，使其拥有最短的等待时间，使收益相对平衡。

5. 总结

本文结合影响出租车决策的五个因素，建立机场出租车载客系统动力学模型，具体分析使机场交通高效运行及出租车司机收益最大化的策略：

当天气状况良好时，出租车司机往往会前往到达区排队等待载客返回市区；当天气恶劣时，出租车司机更倾向于直接放空返回市区；当航班正点到达时，出租车司机可以选择合适的航班时间前往到达区排队等待载客返回市区；当航班延误时，为了避免浪费不必要的时间成本，出租车司机往往会直接放空返回市区；当“蓄车池”出租车数量适量且乘客数量较多时，出租车会愿意前往到达区排队等待载客返回市区；当“蓄车池”出租车数量过于饱和时，出租车会倾向直接放空返回市区；当乘车区乘客数量较多时，出租车司机会愿意前往到达区排队等待载客返回市区；当乘车区乘客数量较少时，出租车司机往往会节省时间成本而直接放空返回市区；当司机有其他原因(如油量不足、家中事务等)发生时，会选择直接放空返回市区。

同时，结合上海虹桥机场的航班情况仿真模拟进行分析，上海虹桥机场出租车司机会选择前往到达区排队等待载客返回市区。最后，结合分类讨论法，将出租车分为三类，出租车司机根据自己所属的类别进入相应的“蓄车池”及上客区接载乘客；结合优先级调度算法，出租车可以进入等待时间最短并且队列最短的出租车排队队列，使其拥有最短的等待时间，使收益相对平衡。