1. 引言
金融市场是经济活动的重要组成成分,对国家、对企业以及对于个人都有着重要的意义。股票市场对于实体经济的影响和作用都是相互的,作为金融市场的一个重要的构成部分,股票市场从它一出现就引起了人们的关注,并与很多人的生活紧密相关。近些年来,我国经济发展态势较好,人们的生活水平也有显著提升,与此同时带来的是手里资金的闲置,简单的银行储存已不能满足人们的需求。随着投资和金融意识的增长,大家的投资需求更多了,与此同时市场上可供选择的投资类型也更多了,股票市场就是其中之一。高风险和高回报是股票市场的特性,长期以来人们被这特性不断吸引到其中,股票市场也逐渐成为大众投资的重要手段之一。
因此,股票价格预测一直是金融市场领域的研究热点。股票市场中的数据包含以下几个特点:第一是数据量非常大,股市每天的交易都会产生大量的数据,用好这些数据,并且找出规律性非常重要;第二是数据间关系的错综复杂,股市中包含相关和不相关的,也包含线性的和非线性的关系;第三是数据的动态性,股市中的数据时刻都在发生变化。一些研究者在对股票进行分析和预测的时候选择建立统计计量模型,由于计量模型对数据有整体性、平稳性、低噪声等非常严格的要求,加上假定限制过多,这对于现实中的股票市场数据往往是很难达到的,所以该模型用于实际的预测中很难得到想要的预测效果。近来更多的国内外学者在对股票进行预测研究时,往往使用机器学习的方法,如逻辑回归、支持向量机和循环神经网络等。
近年来,随着预测要求的精度越来越高且单一浅层的机器学习模型对于股票的波动性、记忆性等特性无法很好的克服等问题的出现,产生了将分解算法与时序预测模型相结合的组合模型。因为股票数据中包含各种影响分量,它们在相互作用时会遮挡我们要识别的规律或让规律扭曲,因此有理由将股票的过程分解为单个分量并单独分析每个分量的规律,从而进一步提高股票预测的精度。常见的分解算法有奇异谱分析(SSA)、经验模态分解(EMD)、集合经验模态分解(CEEMDAN)、变分模态分解(VMD)等,他们被广泛应用在金融时序数据分解中。比如,刘遵雄等通过基于SSA的广义神经预测模型对同方股份的收盘价进行预测,得到了较高的预测精度 [1] 。Cao等将CEEMDAN和LSTM相结合,对全球主要的股市指数的收盘价进行预测,取得了较好的预测结果 [2] 。Niu等使用变分模态分解对伦敦富时指数和纳斯达克指数进行分解,并使用基于注意力机制的门控循环网络进行预测,提高了预测的准确性 [3] 。程文辉等通过VMD对原始金融序列一次分解后又使用EEMD对残差项进行二次分解,之后使用融合FM和LSTM的方法进行预测,得到了较高的预测精度 [4] 。
因此,本文基于将分解算法和机器学习模型相结合的思想,提出了一种基于二次分解与粒子群优化算法优化的支持向量回归和基于注意力机制的长短期记忆网络的混合模型,即S-V-PSAL混合模型,用来进行股票价格的预测。在使用亿纬锂能股票历史数据进行的实证分析中,通过与其他模型进行预测效果的对比,验证了该模型的有效性。
本文余下部分的结构安排如下:第1节介绍奇异谱分析、变分模态分解、支持向量回归和长短期记忆网络模型的基本理论;第2节介绍所提出的S-V-PSAL混合模型的整体结构与具体流程;第3节进行实证分析;第4节中对本文进行总结及未来展望。
2. 相关工作
文章中提出的S-V-PSAL混合模型,综合了奇异谱分析和变分模态分解两次分解以及支持向量回归模型和长短期记忆网络模型。本节先分别对它们进行介绍,以便在前人的基础上提出混合模型。
2.1. 奇异谱分析
奇异谱分析(SSA)是一种处理非线性时序数据的方法,包括统计学和信号处理中的多种方法。SSA先前一直被用于数字信号处理,在1978年被Colebrook应用于海洋浮游生物研究中,随后Hassani将其引入社会科学领域,对美国每月意外死亡人数进行预测 [5] ,现在SSA被广泛应用于气候、环境、社会科学以及金融等多个领域。SSA的主要目的是将原始时间序列分解成不同的成分序列之和,包括长期趋势、噪声项,从而对原始数据进行分析或去噪,继而用于其他任务。
SSA由分解与重建这两个阶段组成,在两个阶段又都包括两个独立的步骤,第一个阶段是将原始序列延时排列,将单变量时间序列增广为多变量序列也即矩阵形式,对其进行奇异值分解。第二个阶段根据特征值对序列分组,形成新的时间序列 [6] 。
2.2. 变分模态分解
变分模态分解(VMD)由Dragomiretskiy在2014年提出,是一种在模态变分和信号处理问题中的自适应、完全非递归的方法,可以根据输入信号的特性确定模态分解的数目K,并匹配每种模态的最佳中心频率和有限带宽 [7] 。VMD的目标是将一个原始输入信号分解成一组离散的具有特殊稀疏性的子信号 [8] ,也即模态。在保证分解序列各个模态的带宽之和最小的前提下,最终获得变分问题的最优解。
2.3. 支持向量回归
支持向量机(SVM)由Vapnik提出,主要应用于模式识别领域,后来发展到回归领域 [9] 。支持向量回归(SVR)就是其在回归领域的应用,这是一种利用核函数检测高维特征空间中最优回归超平面的回归方法。通过输入样本的特征向量,求出输入特征和输出值之间的回归关系,并根据此关系来对未来值进行预测 [10] 。
2.4. 长短期记忆网络
长短期记忆网络(LSTM)在1997年由Hochreiter提出,是一种改进后的循环神经网络 [11] 。LSTM中存在门控单元,可以帮助系统存储更多信息。单元格通过打开和关闭门来决定是否删除或存储信息。单元由四个主要元件组成:输入门、具有自重复连接的神经元、遗忘门和输出门。遗忘门是允许细胞记住或忘记其先前状态的元素。LSTM的具有自重复连接的神经元结构示意图如图1所示。
首先“遗忘门”决定从单元状态转储哪些信息,这个功能需要
(从前一个隐藏层输出)和
(当前输入)共同决定,并通过式(1)输出[0, 1]中的数字,其中1表示“完全保持”,0表示“完全转储”。LSTM决定在单元状态中的存储时有两个步骤。首先,由“输入门”来决定保留的信息,如公式(2)。然后,用tanh层对保留的消息生成向量
来更新单元状态,如公式(3)。公式(4)将单元状态
更新为
。最后“输出门”决定LSTM输出的内容。LSTM首先运行一个sigmoid层,即公式(5),它决定要输出哪个单元状态。并用tanh层把输出取值固定在−1和1之间,并乘以sigmoid层的输出,如公式(6),以此来输出想要的部分。
(1)
(2)
(3)
(4)
(5)
(6)
3. 基于S-V-PSAL混合模型的股票预测
本文提出了一种基于S-V-PSAL混合模型的预测方法来进行股票价格预测。该混合模型首先利用奇异谱分析(SSA)将股票价格数据进行第一次分解,得到长期趋势子序列和噪声子序列,接着用变分模态分解方法(VMD)对噪声子序列进行第二次分解,得到一系列频率不同的子序列IMFs,之后使用支持向量回归模型(SVR)对长期趋势子序列进行预测,并且使用粒子群优化算法(PSO)来确定SVR的最佳参数,包括核函数系数、惩罚因子和epsilon。对于VMD分解之后的子序列,使用基于注意力机制的长短时记忆网络模型(ALSTM)来预测。最后重构各序列得到最终结果。预测的具体流程图如图2所示:

Figure 2. Financial time series data forecasting flow chart based on S-V-PSAL mixed model
图2. 基于S-V-PSAL混合模型的金融时序数据预测流程图
4. 实证分析
4.1. 数据来源
为了验证使用混合模型预测的有效性,使用python从baostock网站获取股票历史数据,进行实证分析。实例中使用的数据为2020年1月2日~2022年12月30日这三年的亿纬锂能股票(股票代码为SZ300014)的历史数据,共728条交易日数据,每条数据包含的特征有open、high、low、close等。部分数据展示如下表1所示。图3展示的是原始股票数据的收盘价序列。
由于数据之间有不同的量纲,为了实验后续的顺利进行,需要对原始数据进行归一化处理,并对处理后的数据以8:2进行划分,前578条数据为训练集,后145条数据为测试集。
4.2. 模型评价指标
下面使用平均绝对误差(MAE)、均方误差(MSE)和决定系数(R2)这三种在回归问题中常用的评价指标,来对预测结果进行评价,以更直观、定量的比较所提出的S-V-PSAL混合模型与对比模型的对股票价格的预测性能。这三种评价指标的计算公式如下式(7) (8) (9)所示:
(7)
(8)
(9)
其中,S是数据长度,y是数据的真实值,
是预测值,
是真实值的平均值。作为评价指标,MAE、MSE的值越小,表明模型预测效果越准确。R2的值越靠近1,表明模型的拟合程度越好。
4.3. 实验结果分析
4.3.1. 二次分解
首先对数据进行一次奇异谱分析,将亿纬锂能股票的收盘价序列以20为窗口长度构造轨迹矩阵,继续对轨迹矩阵进行奇异值分解,得到的奇异值越大表示包含的有用信息更多,绘制奇异值占比图如图4所示,从图中可以看出前两阶包含了90%以上的信息,所以将前两阶作为趋势序列,将三阶以后的部分作为噪声序列,由此将原始数据分解为trend序列和noise序列,如图5所示。
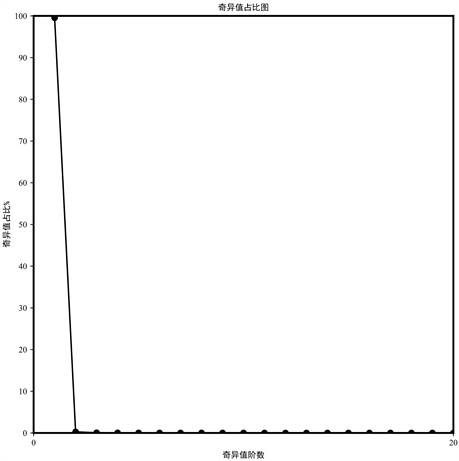
Figure 4. Proportion graph of singular values
图4. 奇异值占比图
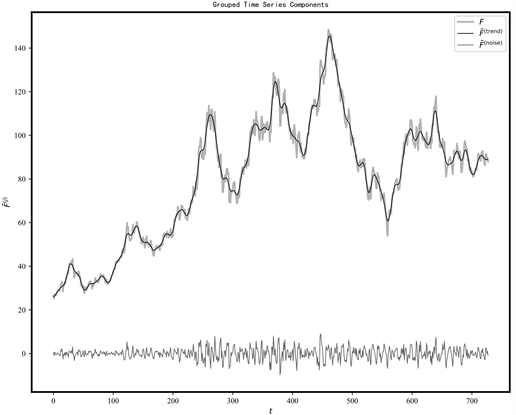
Figure 5. Results of singular spectrum analysis
图5. 奇异谱分析结果
之后,对SSA得到的噪声序列继续进行变分模态分解。选择分解模态的数目为3。noise序列分解得到的模态IMFs如图6所示,残差序列如图7所示。

Figure 6. IMFs of VMD decomposition
图6. VMD分解后的IMFs
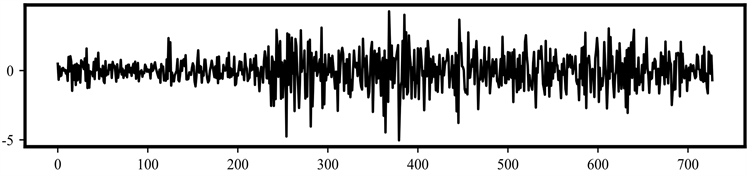
Figure 7. Residual sequence of VMD decomposition
图7. VMD分解后的残差序列
4.3.2. 预测结果
首先使用PSO-SVR对原始序列进行预测,结果如图8所示。
然后分别对SSA得到的trend序列和noise序列进行PSO-SVR预测,结果分别如图9、图10所示。对两段序列得到的预测序列相加,得到SSA-PSO-SVR模型预测结果,如图11所示。

Figure 8. Prediction of original sequence PSO-SVR
图8. 原始序列PSO-SVR预测图

Figure 9. Prediction of trend_PSO-SVR
图9. trend_PSO-SVR预测图
之后对VMD得到的子序列IMF1、IMF2、IMF3和残差序列使用ALSTM进行预测。结果如图12、图13、图14、图15所示。在表2中列出了各IMFs预测结果的评价指标数值。

Table 2. Evaluation index of each IMFs prediction result
表2. 各IMFs预测结果的评价指标
最后,将PSO-SVR预测的trend序列的预测结果和ALSTM预测的IMFs和res序列的预测结果重构,得到的最终预测结果如图16所示。
为了比较所提出的S-V-PSAL混合模型与PSO-SVR模型、SSA-PSO-SVR模型的预测结果,在表3中列出了各个模型的评价指标,可以看出未经过分解的PSO-SVR模型的MAE、MSE最大,R2最小,经过一次分解的SSA-PSO-SVR模型各评价指标均居中,预测效果相比未经过分解的模型较好,而所提出的经过二次分解的S-V-PSAL混合模型的MAE、MSE均最小,R2最大,表示所提出的混合模型的预测效果最好。

Figure 16. Prediction of S-V-PSAL mixed model
图16. S-V-PSAL混合模型预测图

Table 3. Evaluation index of each model
表3. 各个模型评价指标
5. 结语
股票价格时间序列数据具有非线性、非平稳、复杂性高等特点,经过分解,能够一定程度的降低序列的复杂度。本文提出了基于S-V-PSAL混合模型的股票价格预测方法,经过奇异谱分析和变分模态分解二次分解,发挥分解算法的优势,有效降低了数据的复杂度。使用PSO-SVR和ALSTM对分解后的子序列进行预测,再将预测结果重构得到最终预测结果。使用亿纬锂能的股票历史数据进行验证,与PSO-SVR、SSA-PSO-SVR相比,S-V-PSAL混合模型的预测效果较好。
虽然从评价指标看出S-V-PSAL混合模型具有较好的预测效果,但是仍需要对其进一步的改进。本文中对于VMD和ALSTM的参数设置,受人为影响,通过不断地调参来选定,后续考虑使用优化算法或者样本熵的方法来设置参数,使模型效果更优。
基金项目
国家自然科学基金(11961039)。
NOTES
*第一作者。
#通讯作者。