基于标识压缩的Petri网可达状态研究

Research on Reachability of Petri Nets Based on Identifier Compression

摘要: Petri网可以准确地反映在事件(变迁)发生时，系统产生的相应变化。而可达图正是对一个系统所有动态信息的表现。因此，针对复杂Petri网系统初始标识变化导致可达标识剧增这一场景，恰当地保存可达标识就成为了一大挑战。本文针对可达标识的存储，提出压缩标识的算法。通过对需要进行保存的标识进行编码，无需存储实际的托肯数，只需要保存压缩后的标识。在此基础上，进一步提出了去冗余化的实现算法，极大程度上减小了存储标识所需要的内存空间。然后，通过实验，验证了所提出的算法有较好的压缩效果。最后，由于验证算法在压缩标识时需要花费额外的时间，给出了压缩标识算法在CDUA中的实现，并且检验了效果，给出了相应的分析。

Abstract: A Petri net can accurately reflect the corresponding changes in a system when events (transitions) occur. The reachability graph represents all dynamic information of a system. Therefore, in the scenario of a complex Petri net system with a significant increase in reachable markings due to ini-tial marking changes, appropriately storing reachable markings becomes a major challenge. This paper addresses the storage of reachable markings and proposes an algorithm for identifier com-pression. By encoding the markings that need to be saved, the actual token numbers do not need to be stored, and only the compressed identifiers need to be preserved. On this basis, a redundancy elimination algorithm is further proposed, significantly reducing the memory space required for storing identifiers. Then, through experiments, the proposed algorithm’s compression effectiveness is verified. Finally, due to the additional time required for validating the compression algorithm on reachable markings, the implementation of the compression algorithm in CDUA (Compute Unified Device Architecture) is presented, and its effectiveness is examined, along with relevant analysis.

1. 引言

随着以智能制造为核心的工业4.0时代的到来，分布式控制 [1] 变得愈发重要起来。要对这类型系统做出建模，并且所得模型必须能够精准地反映系统中的每个动作，在出现死锁或者陷入故障 [2] 的时候也能够恰当的表达。而使用Petri网建模，正可以满足这些要求。Petri网可以精准地表达分布式系统的初始状态、资源的分配、事件或动作的发生以及故障出现等状况，变迁的发射可以表现出复杂系统的状态变化 [3] 。所以，将Petri网建模理论应用到这类系统的建模中去有着极其重要的意义。

想要用Petri网来准确地表现被建地模系统每个状态的发生，可达图 [4] 是一个较为直观、可靠的方法。在构成可达图的过程中，就需要快速准确地计算出每一个可达状态。所有可达状态组成的集合就被称为可达集 [5] 。

在计算一个Petri网的所有可达标识时，由于初始托肯发生变化，或者是网规模愈发增大，就有可能出现标识数激增，甚至出现状态空间“爆炸的问题”。因此，就需要恰当的存储，尽可能减少占用内存空间。针对这类问题，对可达标识进行压缩是一种较好的策略。而另一种方式是利用OBDD (有序二元决策图)来压缩。OBDD是一种有效的对布尔函数进行操作以及描述的方法 [5] 。针对有界Petri网，把标识转换成对应的布尔变量来存储，添加新标识时，可以复用已经存在的路径。李凤英等人在此基础上，提出了Petri网可达标识的OBDD以及ZBDD表示方法 [6] 。需要注意的是，这类方法是通过复用已有的路径来压缩Petri网的可达标识的，并没有实际针对标识进行压缩。本文提出了可以直接压缩标识的算法，给出了这种算法的具体实现，并且通过算例的仿真来验证了提出算法的可靠性。

2. 相关知识

2.1. Petri网

定义1 [7] ：一个Petri网定义为一个五元组， $PN=\langle P,T,Pre,Post,M_0\rangle$ ，其中：

$P=\left\{P_1,P_2,\cdots ,P_m\right\}$ 代表m个组成库所集合；

$T=\left\{T_1,T_2,\cdots ,T_n\right\}$ 代表n个变迁组成的集合；

$Pre=P\times T$ 代表从库所到变迁的有向弧；

$Post=T\times P$ 代表从变迁到库所的有向弧；

$M_0$ 是初始标识。对应着函数 $M:P=Z^{+}\cup \left\{0\right\}$ ，即给每个库所分配的初始托肯数。

在对系统进行建模分析时，Petri网使用变迁的发射来表征事件的发生。这是一个动态过程，发射一个变迁，会导致对应数量的托肯移动，也就产生了新的标识。将从一个标识到另一个标识，需要经过的标识以及相应的发射变迁，称之为一个发射序列。比如从 $M_0,M_1,\cdots ,M_r$ 这些标识的产生需要经过 $t_1,t_2,\cdots ,t_r$ 这些变迁的发射， $\sigma =M_0{t}_1{M}_1{t}_2\cdots t_r{M}_r$ 就是对应的发射序列。称 $M_0$ 到 $M_r$ 是经过 $\sigma$ 可达的，记作 $M_0[\sigma \rangle M_r$ ，或记为 $M_r=M_0[\sigma \rangle$ 。

定义2 (变迁使能规则) [7] ：如果 $\forall p\in {}^{·}t$ ，有 $M\left(p\right)\ge Pre\left(p,t\right)$ ，那么就称变迁t是使能的。

定义3 (变迁发射规则) [7] ：在标识M下，变迁t的使能导致了新标识 $M_{new}$ 的产生，记作 $M[t\rangle M_{new}$ ，其中 $M_{new}$ 的求取如下：

$M_{new}\left(p\right)=M\left(p\right)-pre\left(p,t\right)+post\left(p,t\right)$

在对一个给定的Petri网结构进行分析并且构建其可达图的过程中，需要计算出每一个可达标识。并且在直接相连的可达标识间，也就是通过某个变迁发射而触发的新旧标识之间，通过有向弧来进行连接。与此同时，为了尽可能降低可达图的复杂性，需要对相同的标识进行去重，这就需要在计算过程中判断这个标识是否存在于现有标识中，如果不存在，就添加这个标识，否则的话，继续进行迭代。

2.2. 通用压缩算法

现在对Petri网可达图的研究中，经常把一个标识看作一个整型数组，数组中每个元素都对应着当前状态下，库所中的托肯数。因此考虑使用无损压缩减少占用的内存。

等长编码压缩 [8] 。使用较为广泛，并且实现也较为简单。应用到可达标识的存储中，其主要思想为，对标识中的各个库所而言，找出最大的托肯数，使用可以表示这个数的最大位数来表示每个库所中的托肯数。

差分编码压缩 [8] 。算法基本思想是，不再保存每个库所对应的托肯数，而是在保留第一个库所的前提下，接下来的每个位置保存当前库所与第一个库所之间的差值。

考虑存储short型(占2个字节)数组的场景，未压缩以及使用两种压缩算法的比较如图1所示。

(a) (b) (c)

Figure 1. (a) Stores an uncompressed array of short data type; (b) Stores a short array with equal-length compression; (c) Stores a short array with delta compression

图1. (a) 存放未被压缩的short型数组；(b) 存放等长压缩的short型数组；(c) 存放差分压缩的short型数组

需要存放(5, 2, 7, 0, 0)的short型数组时，未经过压缩，如图1(a)所示，一共占用10字节的内存空间；经过等长编码压缩，如图1(b)所示，取出数组中最大数为7，每个位置就可以压缩成一个字节来表示，一共需要6字节大小的内存；经过差分编码压缩，如图1(c)所示，也仅需要6字节大小的内存。需要注意的是，虽然使用这两种压缩编码已经在一定程度上减少了内存空间的占用，但是仍然会有冗余位的出现。接下来，提出了去冗余化的改进方式，提高了压缩的质量。

3. 压缩算法实现

在求取Petri网的可达标识时，需要存储已经遍历过的标识，需要添加新标识时，首先对现有的标识进行判重，不重复才会添加到对应的容器中。给定一个未添加到容器中的标识集，按照上述的步骤，经过多次迭代，可以获取到所有的标识。给出可达图的构建伪代码如算法1所示。

Algorithm 1. Petri net reachability graph construction algorithm

算法1. Petri网可达图构建算法

假定一个Petri网的可达标识可以用一个short型数组来表示，也就是说，在任何情况下，一个库所存放的托肯数总是小于等于32,767。

针对上面的可达图构建算法，提出了对标识进行压缩的算法。在存储新标识时，存储经过压缩后的标识，可以在一定程度上减少空间占用。下面给出两种压缩方法以及具体实现。

3.1. 等长编码压缩

对于一个Petri网而言，通常每个库所存放的托肯数是不相同的。因此，可以求出当前标识中最大的托肯数，使用大于等于这个最大值的8的整数次来存放。一般情况下，存放这个最大值所需的字节小于2字节。基于这个角度出发，使用等长编码来压缩可达标识。

求出最大值所需的字节数后，这个标识下，所有库所中的托肯数都使用对应字节数来表示。相较于未使用等长编码压缩的可达标识，压缩率可以使用下面等式来计算：

$\text{Compressionrate}=\frac{{\displaystyle \underset{i=1}{\overset{\text{placeNum}}{\sum }}\max \left(\text{byte\_size}\right)}}{\text{total\_need\_byte}}$

其中：

Compression rate指的是压缩率；

max (byte_size)指的是存放当前标识中最大托肯数所需的字节；

placeNum指的是当前Petri网的库所数；

total_need_byte指的是未进行压缩前，存放这个标识所需的字节数；

使用等长编码压缩可达标识的好处在于使用最小的可满足内存来存放。不会对标识中实际的托肯数做出任何的修改。现给出对可达标识使用等长编码压缩如算法2所示。

Algorithm 2. Fixed-length coding compressed identification algorithm

算法2. 等长编码压缩标识算法

需要注意的是，使用等长编码来压缩Petri网的标识并不一定能够保证压缩效果，如果当前标识中最大的托肯数存放需要2字节，那么对这个标识进行压缩就不会起到效果。为了在一定程度上解决这个问题，提出了基于去冗余化的差分编码压缩方式。

3.2. 差分编码压缩

本文提出一种改进的基于差分编码的Petri网可达标识压缩方法。首先，遍历整个数组，找到最大值以及最小值，求出中值，并且保存中值，而后求出存放最值与中值之间的差值所需的最大位数。为了尽可能的避免冗余位的出现，除了保存中值外，每个对应元素都是用这个最大位数来保存。考虑到差值正负值均有可能出现，对正值不做处理，对负值做取反操作。

使用这种改进的差分编码方式来压缩可达标识的压缩率可以使用下面等式来计算：

$\text{new\_byte}=\text{mid\_byte}+\frac{\max \_\text{bits}\ast \text{placeNum}}{8}$

$\text{Compressionrate}=\frac{\text{new\_byte}}{\text{total\_need\_byte}}$

其中：

mid_byte表示存放中值所需的字节数；

max_bits表示存放差值所需的最大位数；

placeNum表示库所数；

new_byte表示压缩后需要的字节数；

total_need_byte表示未压缩前需要的字节数；

使用这种改进后的压缩算法可以一定程度上增强了压缩效果。并且，尽可能去消除了冗余位。但是，需要注意的是，如果需要再次获取到原标识时，需要进保存的编码进行解码操作。给出对可达标识使用改进后的差分编码压缩的算法，如算法3所示。

Algorithm 3. Improved differential coding compressed identification algorithm

算法3. 改进后差分编码压缩标识算法

4. 实例验证及结果分析

4.1. 可行性验证

用Java编程实现了这两种压缩算法的串行实现。实验用主机主频为2.8 GHz，分配的堆内存为4 Gb。通过一个较为复杂的Petri网结构，首先比较计算得到的可达标识数是否相同。在此基础上，进一步比较压缩前后占用的内存大小。

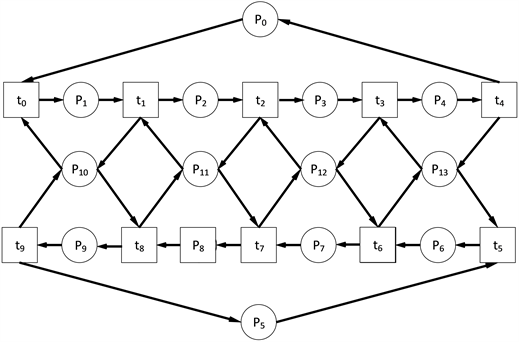
Figure 2. Example of a complex Petri net

图2. 复杂Petri网示例

如图2所示，该Petri网结构是一个由14个库所和10个变迁所组成的。随着初始标识的变化，可达标识数也会随之变化，在比较复杂的网结构中，就会出现状态量激增的情况，甚至有可能导致状态空间“爆炸”。

为了解决这种情况，在允许的情况下，计算出的可达标识集会占用更少的空间；如果需要使用到的内存空间已经超过了可用的上限值，将会能够计算出更多的标识。

需要注意的是，相较于未使用编码压缩可达标识前，虽然能够节省内存空间，但是在进行压缩时，会占用一定的时间，在需要计算的网较复杂时，消耗的时间是不容忽视的。考虑以时间换取空间，做了一些这个方面的权衡。

现给出基于图2的复杂Petri网结构，在变更初始标识的情况下，占用空间的对比如表1，花费时间的对比如表2。

注意的是，下面两表的标识自上而下均为：

$\left[0,5,5,5,5,5,0,0,0,0,0,0,0,5\right]$ ，

$\left[0,9,9,9,9,9,0,0,0,0,0,0,0,9\right]$ ，

$\left[0,11,11,11,11,11,0,0,0,0,0,0,0,11\right]$ ，

$\left[0,15,15,15,15,15,0,0,0,0,0,0,0,15\right]$ 。

Table 1. Comparison of space occupancy before and after encoding compression (unit: MB)

表1. 编码压缩前后占用空间比较(单位为MB)

Table 2. Comparison of time consumption before and after encoding compression (unit: s)

表2. 编码压缩前后花费时间比较(单位为s)

4.2. CUDA并行实现

通过4.1节，验证了使用两种压缩算法可以对大规模Petri网占用的内存空间进行有效的压缩，但是会花费额外的时间。使用CUDA来并行化计算Petri网的可达标识，可以有效的减少花费的时间。在图2所示的Petri网复杂示例中，不断变更初始标识，比较使用CUDA前后以及使用基于两种压缩标识的方法改进的CUDA并行化算法所花费的时间(见表3)。

Table 3. Comparison before and after CUDA improvement

表3. CUDA改进前后对比

使用CUDA实现了并行计算改进前后求取Petri网可达标识集的算法，并且比较了花费的时间。通过表3可以较为直观的看出来，使用CUDA有效的加快了计算效率，但是使用两种压缩标识的算法后，会消耗额外的时间。这种在时间的花费上并不是无意义的，由于性能所限，CUDA使用memcpy函数在主机端和设备端进行数据拷贝时，会受到设备端内存和全局内存大小的影响。

并行计算中，程序并行化的效果以及性能可以使用加速比的概念来描述。加速比是由美国计算机科学家吉恩·阿比达尔提出的，可以用下面公式计算：

$K=\frac{W_s+W_p}{Ws+\frac{W_p}{p}}$

其中：

K为并行计算加速比；

W_s为待解决问题的串行分量；

W_p为待解决问题的并行分量；

p为系统处理器的个数。

对改进CUDA代码前后所花费时间求取加速比，可以更加直观的表现出并行计算的加速效果。

Table 4. Comparison of speedup before and after CUDA improvement

表4. CUDA改进前后加速比对比

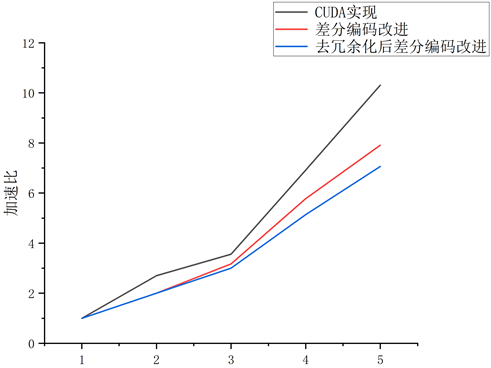
Figure 3. Speedup of various parallelization algorithms

图3. 各种并行化算法加速比

在如图3所示的并行化算法加速比对比图中，可以较为直观的看出来，使用CUDA对Petri网求可达集有明显的加速效果，但是使用压缩标识的算法后，会造成一定的影响。在随着标识数剧增的情况下，这种影响是不容忽略的。但是在使用CUDA对这两种算法做了并行方面的加速后，在花费时间上仍然有较大的改善。

5. 结束语

提出了一种可达标识压缩的思路。使用两种不同的编码方式。在计算Petri网可达标识集时，规模越大，传统算法所需的空间会越大，而使用压缩标识的效果会更好。通过与未压缩前的所需的时间和占用的内存空间对比，验证了所提出方法的有效性。

在判断提出的算法对于存储空间有着明显的压缩效果以后，进一步使用CUDA实现并行加速。通过表4以及图3，可以较为直观地看出来，使用CUDA对Petri网求可达集有明显的加速效果，但是使用压缩标识的算法后，会造成一定的影响。在随着标识数剧增的情况下，这种影响是不容忽略的。

下一步的思路主要是寻找更适合压缩Petri网可达标识的编码方式或者算法，从而进一步提高空间利用率。