高速公路ETC车道车流的优化模型研究

Study on the Optimization Model of Traffic Flow in Toll Lanes of Expressway Toll Stations

摘要: 高速公路ETC收费车道的过车能力在大部分时段存在冗余，且待收费车辆的车道选择惯性行为形成其不同的通行强度。为最大化各ETC收费车道效用及防止车流高峰时段惯用车道的交通拥堵，分析ETC车道饱和通行能力的基础上拟合其饱和车头时距，并提出一种ETC收费车道车流的优化模型：基于车道车流的饱和车头时距占比和差异，模型动态调整收费车道开放数及再分配各车道交通流，进而平衡各车道的通行强度及提高通行效率。基于贵阳西收费站而求解模型及仿真的结果表明：根据通车情景调整收费车道开放数且优化车流后，站点各车道的通行强度均衡值均提高20%以上、通行车辆延误时间缩短5%到8%。站点车流稳定条件下，根据车道利用率调整收费车道开放数并再分配其静态车流的方法可使高速公路ETC车道的通车效率更高，其车流优化的思路可为站点的智慧化管理提供参考。

Abstract: The passing capacity of the expressway ETC toll lane is in excess most of the time, and the lane selection inertia of the vehicle forms its different traffic intensity. To maximize the utility of each ETC toll lane and prevent traffic congestion in the habitual lane during peak hours: firstly, we calculate and fit the saturated headway of the ETC toll lane; secondly, we propose an optimiza-tion model of the traffic flow of the ETC toll lane. Based on the proportion and difference of the saturated headway of the lane traffic, we dynamically adjust the number of toll lane openings and redistribute the traffic flow of each lane, to balance the traffic intensity and improve the traffic efficiency of each toll lane. Based on Guiyang West Toll Station, the results of solving the model and simulation show that: after adjusting the number of toll lanes open according to the opening scenario and optimizing the traffic flow, the traffic intensity balance value of toll lanes increases by more than 20%, and the delay time of passing vehicles is shortened by 5% to 8%. Under the condition of stable traffic flow at the station, the method adjusts the number of toll lane openings according to the utilization rate of the lane. By distributing its static traffic flow, the opening efficiency of the ETC lane of the expressway is higher. The traffic flow optimization can provide a reference to manage the station intelligently.

1. 引言

随着ETC收费的广泛应用和收费平台的智慧化迭代，高速公路收费站的整体收费能力大幅上升。ETC收费车道与待收费车辆的距离不同，其车道的通行强度相差较大且偏离主路的收费车道车辆到达量较小 [1] 。大部分时段，低通行强度的ETC收费车道的利用率较低，而车流高峰时段时，高通行强度的惯用车道率先出现交通拥堵现象。现阶段，收费站人工调整ETC收费车道开放数及平衡交通流的管理水平较低。因此，探讨如何动态调整ETC收费车道的开放数以及智慧优化其车道车流的策略具有十分重要的应用意义。

高速公路收费站的车道开放策略和车流分配效果直接影响其运营效率和经济效益高低 [2] 。当前，学界针对高速公路收费站的研究主要为ETC收费站的交通流特征、站点布局的优化和站点车道的选择行为等 [3] 。其中，已有部分学者分析交通流对收费站整体通行效率及运营效率的影响 [4] ，部分学者侧重分析收费高峰时段用户的延误时间和出行成本 [5] 。待收费车辆经匝道交织区驶入ETC收费车道的车速较低，其行驶情景与城市道路交叉口转向行为类似。此外，车流饱和流率广泛用于道路交叉口的智能交通方案研究 [6] [7] 。因此，本文基于各车流的饱和度调整车流利用率。不同交通状态下，各车道的饱和车头时距占比各异。现阶段，基于饱和车头时距分析ETC收费车道通行效率的研究较少。实际上，高速公路收费站通行车辆的全时段过车数据涵盖饱和、非饱和等多种交通状态 [8] 。非拥堵时段，通行强度较低的收费车道的车辆通行量接近零；通行车辆较密集时，收费车道的车头时距较小且饱和车头时距出现概率较大。综合以上研究，本文首先以高速公路ETC收费车道的饱和车头时距分析为基础，并依据其通行强度关系建立ETC收费车道车流优化模型。其次，基于案例站点对优化模型进行求解而得到相应的车道调整策略和交通流再分配方案。最后，对比和仿真各车道优化前后的车流状况而论证模型的可行性和有效性。

2. 饱和车头时距分析

2.1. ETC收费车道饱和通行能力分析

收费车道通行能力与车身系数、通行限制速度及驾驶人行为等系列因素有关 [9] 。本文参考ETC单车道的通行能力计算方法 [10] 及基于通行车辆的安全时距和过车延误时间，得出ETC收费车道的一般通行能力 $C_E\left(K\right)$ 的计算公式(1)：

$C_E\left(K\right)=\frac{3600}{T_E\left(K\right)}=\frac{3600}{\left(S_{安}+L_{车}\right)\cdot 3.6/v_{设}+t_{延误}}$ (1)

其中 $T_E\left(K\right)$ 为收费站K的ETC收费车道最小车头时距均值； $L_{车}$ 为通行车辆平均长度； $v_{设}$ 为收费车道的限制速度； $t_{延误}$ 为车辆通过ETC收费车道的延误时间，其值为ETC收费车道平均服务时间 $t_{服务}$ 与车辆通过收费车道时间 $L_{收费车道}/v_{设}$ 的差值； $S_{安}$ 为ETC收费车道的车辆安全间距。

高速公路的通行能力与其车道宽度、侧宽及路侧干扰物等因素相关 [11] 。收费站一般地处平坡，其ETC收费通道数大于3且路侧较宽。因此，车道侧宽修正系数和路侧干扰系数均取为1，而车道宽度对通行能力的修正系数 $f_w$ 取值参考高速公路车道各宽度对应的修正系数表 [12] 。各收费站服务群体存在差别 [13] 。通行车辆类型占比不同，其收费车道对应的通行能力有所不同，本文根据ETC收费车道过车车型及其占比修正ETC收费车道饱和通行量，具体方法为：合并一型客货车为小型车、合并其余类型车辆为大中型车，并按照大中型车与小型车的通行能力转换关系设置通行车辆类型修正系数 $f_t$ [14] (见表1)。收费车道的通行能力与其站点服务水平紧密相关。代收费车辆对车辆行为变化较敏感 [16] ，借鉴公路交通流特征分析中驾驶体验分级其服务水平的方法 [15] ，本文以三级服务水平的V/C值为界限而划分站点交通流是否繁忙。因此，设定高速公路收费站K的ETC收费车道的饱和通行能力 $C_p\left(K\right)$ (pcu/h)，其计算公式如下：

$C_p\left(K\right)=C_E\left(K\right)\cdot f_w\cdot f_t\cdot V/C$ (2)

Table 1. Correction factors for traffic types

表1. 通行车辆类型修正系数

2.2. 饱和车头时距拟合

部分学者使用路段服务强度表示路段车道承担的交通流量占最大路段车道交通量的比值 [16] 。其中，ETC收费车道通行强度越大，通行车辆越密集，收费车道的车头时距越小且饱和车头时距出现的概率越大。由于混合车流对车头时距影响较大 [17] ，本文借鉴期望车速 [18] 和饱和车头时距 [6] 的计算方法并基于通行强度，而得到收费车道相对空闲或饱和状态对应的车头时距分位点。设饱和车流阈值 ${t^{\prime }}_{k,s}$ 为收费车道k的车流状态的车头时距分位点，其计算公式为(3)：

$P\left(t_{k,s}\ge {t^{\prime }}_{k,s}\right)=1-w_k$ (3)

其中车头时距 $t_{k,s}$ 为ETC收费车道k中前后待收费车辆成功通过闸机的第d条和第 $d-1$ 条收费交易记录间隔(精确到s)；ETC通行强度 $w_k$ 为收费车道k实时交通量与饱和通行量的比值，其计算公式为(4)：

$w_k=AH{V}_k/C_p\left(K\right)\left(k=1,2,3,\cdots \right)$ (4)

其中 $AH{V}_k$ 表示站点K中收费车道k的每小时通行量均值。

部分学者使用数据驱动的方法分析通行车辆饱和状态对应的高斯分布均值 [19] 。考虑偏小车头时距对ETC收费车道饱和车头时距均值的影响，本文将站点K所有ETC收费车道中小于 ${t^{\prime }}_{k,s}$ 的车头时距合并为饱和车头时距集合 $\left\{t_K\right\}$ ，并使用对数正态分布拟合站点期望饱和车头时距 ${\bar{T}}_K$ 。

3. ETC收费车道车流优化模型

本节ETC收费车道车流优化模型包括饱和车头时距的平衡模型和交通流分配模型。

3.1. 饱和车头时距的平衡模型

在微堵时段内，站点车流连续 [20] ，过小的周期内优化站点车流的应用价值较小。参考以往研究中按每小时分析收费车道的通行能力 [1] [5] ，本文首先以30 min为时间间隔对车道流量进行饱和分析，并将前一周期车流的饱和车头时距分析结果用于后一周期的车道优化和流量分配。设ETC收费车道k的 $T-1$ 周期的车道利用率 $C_{T-1}{}_{,k}$ ，其值为期望饱和车头时距 ${\bar{T}}_K$ 与车头时距 $t_{k,s}$ 均值之比，即计算公式(5)：

$C_{T-1}{}_{,k}=\frac{{\underset{\dot{}}{T}}_K}{{\displaystyle \underset{s=1}{\overset{m}{\sum }}{t}_{{}_{k,s}}}/m}\left(s=1,2,\cdots ,m\right)$ (5)

其中m为收费车道k分析周期内通行车辆数。

车流优化需首先开启或关闭通行强度异常的ETC收费车道而调整站点整体车流的均衡空间。因各ETC收费车道对车流的饱和车头时距的影响不同，引入优化差异系数 $q_{T-1,k}$ 表示收费车道车流调整空间以明确其车道开启和关闭的优先顺序，其计算公式见(6)：

$q_{T-1,k}=C_{T-1,k}/w_k$ (6)

为明确ETC收费车道的优化方案和车流转移方向，将通行强度 $w_k$ 按大小排列，并以 $q_{T-1,k}=1$ 为界依次命名为 $k_1,k_2$ ，情景化车道的通车状态和优化思路如下：

情景1：站点仅开通部分车道且皆为繁忙状态，即全部营运车道的利用率大于其平均通行强度(所有 $q_{T-1,k_2}=0$ )，则T周期开启 $k_2=j$ 收费车道。

情景2：站点仅开通部分车道且存在空闲状态的车道，即利用率最小的营运车道小于其平均通行强度(存在 $q_{T-1,k_2}=0$ 且 $q_{T-1,k_2}<1$ )。当关闭营运车道 $k_2=j$ 车道而转移的车流量大于其余已开通车道的调整空间总和，即满足式(7)，则T周期关闭 $k_2=j$ 收费车道；否则，维持原有车道数。

$C_p\left(K\right)\cdot w_{k_2=j}\cdot q_{T-1,}{}_{k_2=j}<C_p\left(K\right)\cdot \left[{\displaystyle \underset{k_1=1}{\overset{i}{\sum }}{w}_{k_1}\cdot \left(q_{T-1,}{}_{k_1}-1\right)+{\displaystyle \underset{k_2=1}{\overset{j-1}{\sum }}{w}_{k_2}}\cdot \left(1-q_{T-1,}{}_{k_2}\right)}\right]$ (7)

情景3：站点已开通所有车道且皆处于繁忙状态，即所有车道的利用率大于其平均通行强度(不存在 $q_{T-1,}{}_{k_2}$ )，则T周期维持原有车道数。

情景4：站点已开通所有车道且存在空闲状态，即全部车道中，利用率最小的收费车道小于其平均通行强度(存在 $q_{T-1,}{}_{k_2}$ 且不为0)。当关闭 $k_2=j$ 车道而转移的车流量小于其余已开通车道的调整空间总和，即满足公式(8)，则T周期关闭 $k_2=j$ 收费车道；否则，维持原有车道数。

由于车道车流优化优化前后站点整体车流量相等，因此饱和车头时距的平衡模型的目标函数和约束条件分别为式(8)和式(9)：

$\min J_1=p\left(T\right)-MD=\sqrt{\frac{{\displaystyle \underset{k=1}{\overset{i+j}{\sum }}{\left(w_{T,k}-{\mu }_{w_{T,k}}\right)}^2}}{i+j}}-MD$ (8)

${\displaystyle \underset{k_1=1}{\overset{i}{\sum }}{C}_p\left(K\right)}\cdot w_{k_1}\cdot \left(q_{T-1,k_1}-q_{T,k_1}\right)={\displaystyle \underset{k_2=1}{\overset{j}{\sum }}{C}_p\left(K\right)}\cdot w_{k_2}\cdot \left(q_{T,k_2}-q_{T-1,k_2}\right)$ (9)

其中M为相当大的正数；D为T周期收费车道动态调整量； $w_{T,k}$ 为优化后车道k的通行强度，其值为T周期进入车道k的交通流量 $f_k$ 与车道实际饱和通行量 $C_p\left(K\right)$ 之比； $q_{T-1,k}、q_{T,k}$ 为优化前后车道k的优化差异系数。

3.2. 交通流分配模型

高速公路收费站的交通流分配为动态交通用户均衡过程。部分学者已证明信任诱导车道信息产生的换道行为比例与诱导信息为出行者节省的出行时间均值有关 [21] 。本文根据全时段的车辆交易数据中各车道的通行强度均值差异包含时间节省信息，而以各车道相对流量表示车辆发生换道行为的比例，设T周期经诱导驶入收费车道k的车辆比例 ${\theta }_k$ ，其计算公式为(10)：

${\theta }_k=\left(\frac{{\bar{T}}_K}{w_{T-1,k}}-\frac{{\bar{T}}_K}{w_k}\right)÷\frac{{\bar{T}}_K}{w_{T-1,k}}=\frac{w_{T-1,k}-w_k}{w_k}$ (10)

其次，与道路交叉口信号诱导情景一致，引入诱导信息的控制系数 ${\tau }_{T,K}$ 表示车流诱导效果并设定周期T的收费车道k的诱导信号比为 $a_k$ ( ${\displaystyle \underset{k=1}{\overset{i+j}{\sum }}{a}_k=1}$ )，则收费车道k最大诱导能力 $C_{\max }^k$ 的计算公式为(11)：

$C_{\max }^k=C_p\left(k\right)\cdot w_k\cdot {\displaystyle \underset{k=1}{\overset{j}{\sum }}{q}_{T-1,k}\left(1-{\tau }_{T,K}\right)\cdot {\theta }_k}$ (11)

其中 ${\tau }_{T,K}=1$ 表示T周期收费车道k参与诱导信号输出；反之， ${\tau }_{T,K}=0$ 表示收费车道k的诱导信号处于停用。

由于流入车道k的实际车流量受已有车流的路阻影响，本文参考BPR路阻函数计算路段出行时间的方法 [22] 而设定收费车道k所需的行驶时间为 $t_k\left(x_k\right)$ ，计算公式如下：

$t_k\left(x_k\right)=t_0\cdot \left[1+\alpha {\left(\frac{C_p\left(K\right)\cdot w_{T-1,k}}{C_p\left(K\right)\cdot w_k}\right)}^{\beta }\right]={\bar{T}}_K\cdot \left[1+\alpha {\left(\frac{w_{T-1,k}}{w_k}\right)}^{\beta }\right]$ (12)

其中 $t_0$ 为自由车流通过路段a的时间，其值为期望饱和车头时距 ${\bar{T}}_K$ 。

均衡过程实则为交通流的非线性最优控制问题 [23] ：部分驾驶者以旅行时间最短为目标，因信号诱导改变原行驶路径而使得各车道车流相对均衡，从而自动提高收费站整体利用效率。因此，交通流分配模型中各车道车辆行驶时间的目标函数为计算公式(13)，且受约束条件(10)到(12)限制。

$\min J_2={\displaystyle \underset{k=1}{\overset{i+j}{\sum }}{\displaystyle \underset{0}{\overset{x_k}{\int }}{t}_k}\left(x_k\right)\text{d}x}$ (13)

其中 $x_k$ 为车道k的交通量。

4. 求解算法

收费车道车流优化模型的求解步骤以下：

步骤一，求解饱和车头时距的平衡模型：基于公式(5)~(9)计算各车道优化差异系数 $q_{T-1,k}$ 且识别站点情景而得到车道的动态调整数D和平衡量 $E_k$ ；

步骤二，求解交通流分配模型：参考交通流分配的迭代算法 [24] ，求解各车道的车流迁移过程如下：

1) 初始化，令迭代次数 $n=0$ ，基于公式(12)得到车流流入的收费车道的初始路阻值 $t_k^0\left(x_k\right)$ (交通流分配中，只有信任诱导信息的通行车辆会改变原行驶路径，则流入车流的收费车道的初始路阻值为该车道的行驶时间函数)；

2) 迭代，令迭代次数 $n=n+1$ ，计算第n次迭代的 ${\theta }_k^n$ 、 $t_k^n\left(x_k\right)$ 和 $C_{\max }^{k,n}$ ，并在 $E_k$ 和 $C_{\max }^{k,n}$ 的限制下对车流进行全有全无分配而得到第n次经诱导新进入车道k的交通量 $f_{诱}^{k,n}$ 和其诱导信号比 $a_k^n$ ( $a_k^n=f_{诱}^{k,n}/C_{\max }^{k,n-1}$ )；

3) 判定，当信号比 $a_k^n$ 和为1时，即满足公式(14)，进行步骤4)；否则，返回步骤2)；

${\displaystyle \underset{n=1}{\overset{\max }{\sum }}{\displaystyle \underset{k=1}{\overset{i+j}{\sum }}{a}_k^n}=}1$ (14)

4) 结束，计算优化后车流量 $f_k$ 、 $p\left(T\right)$ 及 $J_1$ 值。

5. 实例分析

5.1. 研究区域和数据来源

本文的研究区域为贵阳市的贵阳西收费站。按小时统计贵阳市的所有收费站的车流分布特征，结果显示其每天的通行车流量表现为早晚双高峰特性。其中，贵阳西收费站作为沪昆高速重要的出入口，其出口共包含8条ETC车道，交通通行量多，可作为代表站点而分析。研究数据来源于该市交通大数据研发中心，共获取2021年节假日期间3,837,478条车辆交易记录比。

5.2. 饱和车头时距计算

参照交通运输部路网中心印发的《标准化ETC专用车道总体技术方案》(下称《技术方案》)中 $S_{安}$ 为26.2 m； $L_{车}$ 取站点车长一般值4 m；依据《技术方案》 $t_{服}$ 取值3 s、 $L_{收费车道}$ 取值16 m，基于公式(1)，得到 $C_E\left(K\right)=765\text{pcu}/\text{h}$ 。其次，根据贵阳西收费站的车道宽度(3.5 m)和全年大客货车车辆占比(3.53%)取相应 $f_w$ 和 $f_t$ 值(0.97、0.898)，且对照三级服务水平 $V/C$ 取0.65，基于公式(2)得到 $C_p\left(贵阳西\right)=433\text{pcu}/\text{h}$ 。再者，计算收费车道k的通行强度 $w_k\left(k=1,2,\cdots ,9\right)$ ，进而得出车头时距集合 $\left\{t_{贵阳西}\right\}$ ，并通过MATLAB拟合期望饱和车头时距 ${\bar{T}}_{贵阳西}$ (精确到s，其值为8 s)。

5.3. 车流优化结果

参考贵阳西收费站的双高峰特征及凌晨车流的低密度现状，本小节取08:00到08:30、17:00到17:30和00:00到00:30三个典型时间段的通行车辆数据而计算各车道的 $q_{T-1,k}$ 大小，进而识别其对应的通车情景及车道调整策略，且进一步迭代求解模型而得到优化前后的服务平衡函数值(分别为参数1和参数3)和服务平衡参数变化率(参数2)，三时段的通车情景及优化策略如表2所示：三时段的车流优化后，站点服务平衡参数变化皆大于22%；时段3与时段1或2对比，即与增加收费车道开放数或维持原有收费车道数相比，关闭站点闲余车道得到的服务平衡函数值最小；时段3的车流量较小，关闭闲余车道后，站点车流的平衡分配效率(73%)较高。以上结果说明，收费车道开放数调整后，各车道通行强度的平衡参数相对提高，且车流到达量较少、关闭闲余车道得到的车流平衡分配效率较高、其服务平衡函数值较小。

Table 2. Traffic optimization results in three periods

表2. 三时段车流优化结果

5.4. VISSIM仿真模拟

该小节以贵阳西收费站的实际几何、减速区域和通行量为仿真基础并设计相应车辆线路模拟各车道通行车辆的决策行为，且进一步分析车流优化前后拥堵指标的变化和通行效率差异：如图1所示，时段3、时段1和时段2的车辆通行量依次递增，而优化后其行程总时间均值缩小百分比也依次递增，如时段3车流到达量较小，其延误时间和行程总时间较小且优化后两变化率较小，分别为−5.97%、−0.45%。以上结果说明，与车道变化数无关，通行量越大的站点，车流优化对其行程总时间和延误时间的缩减效果越大。

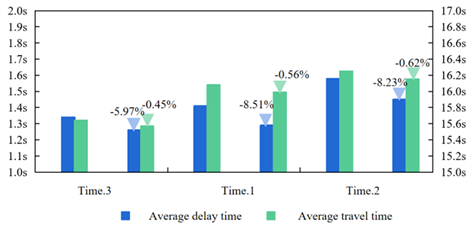
Figure 1. Changes in congestion indicators before and after traffic flow optimization

图1. 车流优化前后的拥堵指标变化

6. 结论

本文首先计算ETC收费车道的一般通行能力，并考虑车道环境、通行车辆类型和站点服务等因素分析其实际饱和通行量；其次，基于期望车头时距占比确定各车道利用率并情景化典型通车状况和车道优化思路，进而平衡车流的饱和车头时距以均衡各车道的通行强度；最后，根据案例的车流数据和通车环境求解模型及仿真结果，得出以下结论：一、收费车道数的调整可平衡各车道的通行强度，且车流量越少时关闭闲余车道得到的车流平衡分配效率较高。二、各车道车流经诱导后其平衡参数均优于原行驶情景，且车流量越小时车流路径变化数较少，其平衡分配效率较高。三、通行量越大的站点，车流优化对其行程总时间和延误时间的缩减效果越大，且与车流优化中的车道开放数无关。本文分析ETC收费车道的通车状态进而通过模型动态调整站点车道开放数及平衡各车道车流压力，该思路为站点的通行效率提升和收费车道拥堵现象的治理提供了借鉴。

基金项目

贵州大学“研究基地及智库”重点专项课题(GDZX 2021030)和贵州大学人文社会科学一般项目(GDYB2021020)。