基于K近邻算法和混合模型的短期交通流预测

Short-Term Traffic Flow Forecast Based on K near Neighbor Algorithm and Hybrid Model

摘要: 道路拥堵情况由于车辆数量的不断增加而一直存在，及时、准确地进行交通流预测仍是研究的重点。由于交通流数据是庞大的、复杂的，本研究使用KNN算法对数据进行挑选，选择与目标监测点相关性更高的数据，将其输入到CNN-GRU-ATT模型中，对交通流数据进行预测。模型中的CNN层提取特征，GRU层描述时间趋势，ATT层实现对关键信息的关注。实验发现：该模型与其他基线模型相比，模型精度更高，MAPE最高降低了28.33%；与未引入KNN算法相比，模型拟合优度有所提升，达到了97.79%。

Abstract: Road congestion has always existed due to the increasing number of vehicles, and traffic flow fore-casting in time and accurately is still the focus of research. Because traffic flow data is huge and complex, this study uses the KNN algorithm to select the data, select data with higher correlation with the target monitoring point, and enter it into the CNN-GRU-ATT model. Perform predictions. The CNN layer extracts feature in the model, the GRU layer describes time trends, and the ATT layer achieves attention to key information. The experiment found that compared with other baseline models, the model has higher accuracy, and MAPE has reduced up to 28.33%; compared with the KNN algorithm, the model fitting superiority has improved, reaching 97.79%.

1. 引言

随着社会科技、经济的发展，汽车数量迅速增加，交通拥堵情况也随之出现。而智能交通系统(ITS)的建设可以有效缓解道路拥堵，缩短出行时间。及时、准确地进行交通流预测必不可少。

早期的交通流预测主要是基于统计分析的，例如自回归、移动平均等模型，这些模型易于理解，但对数据缺失情况难以处理。目前常用的模型分为单一模型的优化和混合模型。其中XGBoost [1] 、SVR [2] 、BP [3] 、LSTM [4] 、BILSTM [5] 、GRU [6] 模型受到广泛使用。但单一模型的精度可进一步提升，因此出现了一系列优化算法，例如自适应天牛须搜索算法(BAS) [7] 、灰狼算法 [8] [9] 、遗传算法 [10] 、蚁群算法 [11] 、鲸鱼算法 [12] 等，均发现模型精度有所提升。当前混合模型更是交通流预测研究的主要潮流。卷积神经网络能够用来提取特征，与上述单一方法混合有较好的模型精度 [2] [4] [13] 。基于交通流数据的复杂性和冗余性，K均值聚类 [14] 被用于数据的预处理，选取与目标监测点相关性更高的监测点数据。Zhuang等 [15] 充分考虑交通流的空间相关性，提出先使用K近邻算法对站点数据进行空间筛选，选取相关性高的点，再输入模型进行预测，性能较LSTM模型提高了19%。

自2014年注意力机制的提出，其迅速成为研究热点。它能聚焦关键信息，减少干扰。Li等 [16] 在模型中加入了自注意力机制，可以抑制长期时间序列信息的丢失，有效提高预测精度。除考虑时间、空间维度外，有的文章也考虑了其他因素的影响。Ma等 [17] 将温度、降水量等气象数据与交通流数据进行融合，发现模型效果较好。

本研究基于英国高速公路数据，建立了KCNN-GRU-ATT模型来更好地预测短期交通流，KNN算法对大量数据进行挑选，选择与目标监测点距离更近的监测点数据，CNN层用于提取特征，GRU层用于时间趋势的描述，ATT层用于聚焦关键信息。

2. 模型及算法介绍

2.1. KNN算法

KNN的核心思想是计算不同特征值之间的距离，找到最接近目标点的点，并通过加权平均得到结果。本研究采用欧式距离来选择交通流的相关性。KNN方法是一种典型的基于数据挖掘的方法，传统的未经处理的数据库是巨大的，难以处理的。因此适当地对数据进行预处理，能较好的压缩数据库，并提高预测性能。

KNN方法步如下：给定一个数据库，包括历史数据和当前数据；确定K的初始值；计算新目标监测点数据与其他数据之间的欧式距离，并按升序排序；根据误差函数，选取最优K值，得到与目标监测点数据K个最近的邻居作为后续模型的输入。

欧式距离的计算公式如下：

$d_i=\sqrt{{\displaystyle \underset{k}{\sum }{\left(x_0\left(k\right)-x_i\left(k\right)\right)}^2}}$ (1)

其中， $x_0\left(k\right)$ 为目标监测点在 $k$ 时刻监测到的交通流， $x_i\left(k\right)$ 为第 $i$ 个监测点在 $k$ 时刻监测到的交通流。

2.2. KCNN-GRU-ATT预测模型

本文通过建立KCNN-GRU-ATT模型来对交通流进行预测，模型整体框架如图1所示。

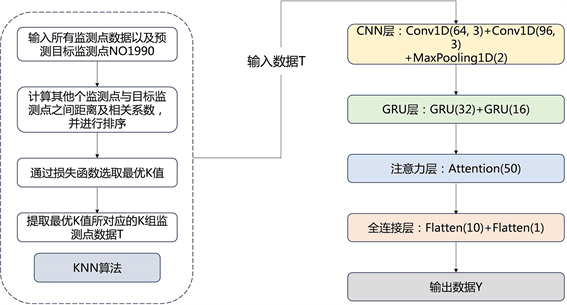
Figure 1. Model process and parameter chart

图1. 模型流程及参数图

1) KNN算法。通过选取最优K值，得到后续模型的输入数据。

2) CNN层。主要包括两层一维卷积层、一层最大池化层。卷积层可以提取特征，而最大池化层对上述特征进行挑选，防止过拟合；

3) GRU层。主要接收上层的输出数据，使用两层GRU层可以更加充分的提取潜在信息；

4) 注意力层。GRU层会随着时间长度的增加而出现信息丢失和梯度消失问题。注意力机制可以保留重要信息，减少其他信息的干扰；

5) 输出层。本文建立两层全连接层，最终输出预测数据。

3. 数据来源及预处理

3.1. 数据来源

本文使用数据为2023年1月1日到2月28日共2个月的英国高速公路M25上46个摄像头监控的交通流数据，以15 min为时间间隔，每个摄像头各采集5664条数据。

3.2. 数据预处理

由于收集到的数据中存在缺失、异常等问题，需要对数据进行预处理。删除缺失严重的6个监测点数据，使用箱线图进行异常值检验时，发现并不存在异常值。但是查看数据之后，发现存在一些不切实际的“0”值，因此将上述异常值当作缺失值进行处理。考虑到交通流数据的交替情况，使用均值替代有所不妥，本文使用前值进行填补。本文对数据进行归一化，使用的是 $\min -\max$ 方法，公式如下：

${x^{\prime }}_i=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }},$ (2)

其中， ${x^{\prime }}_i$ 为归一化后数据， $x_i$ 为原始数据， $x_{\min }、x_{\max }$ 分别为最小、最大值。

4. 实验结果与分析

4.1. 评价指标

本文采用四种回归算法中常用的评价指标来评价模型的效果，分别是 $R^2$ 、RMSE、MAE和MAPE，计算公式如下：

$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^n{\left(y-\hat{y}\right)}^2}}{{\displaystyle {\sum }_{i=1}^n{\left(y-\bar{y}\right)}^2}}\text{,}$ (3)

$RMSE=\sqrt{\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left({\hat{y}}_i-y_i\right)}^2}},$ (4)

$MAE=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|{\hat{y}}_i-y_i\right|},$ (5)

$MAPE=\frac{100\%}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|\frac{{\hat{y}}_i-y_i}{y_i}\right|}.$ (6)

4.2. 实证分析

本文采用PYTHON软件进行模拟研究。为了验证K近邻算法中K值是否对交通流预测结果产生影响，因此选择不同K值进行预测。结果显示，不同的K值对预测性能有显著影响。由图2可以看出，当K = 5、6、9，即相关检测点个数为5、6或者9时，预测效果最好，损失值达到最低。

Figure 2. Different K values corresponding to loss values

图2. 不同K值对应的损失值

为了更直观地观察多个监测点之间的数据相关性，将所有监测点的一天数据共96个样本进行可视化。从图3可以观察到，NO550、NO5066、NO10349与其他监测点的数据差异较大。之后对所有监测点的与目标监测点的相关性进行分析，从图4可以发现相关性系数在98%以上的有5个监测点，分别是NO547、NO5875、NO4145、NO2097、NO3437。

Figure 3. All monitoring points one day data distribution map

图3. 所有监测点一天数据分布图

Figure 4. Analysis of the correlation point of all monitoring points and target monitoring points

图4. 所有监测点与目标监测点的相关性分析

为了找出最优K值，将K = 5、K = 6、K = 9分别进行建模，得到的模型结果见表1。从表1可以看出，K = 6时， $R^2$ 、RMSE、MAE、MAPE分别为0.9779、59.7029、40.0641、0.0898，预测结果略优于K = 5和K = 9时。从表2可以看出，K = 6时，对应的监测点编号分别为NO547、NO5875、NO4145、NO2097、NO3437、NO2992。

Table 1. Evaluation indicators corresponding to different K values

表1. 不同K值对应的评价指标

Table 2. Monitoring point combination corresponding to different K values

表2. 不同K值对应的监测点组合

为了进一步评价KCNN-GRU-ATT模型的有效性，本文选择SVR、LSTM、GRU、CNN-GRU、GRU-ATT、CNN-GRU-ATT模型作为基线模型进行对比。从图5可以看出，SVR、LSTM对数据的拟合效果较差，之后绘制一天的数据拟合效果图(见图6)，发现GRU模型对最高值处的拟合效果较优，而对持续上升的数据拟合效果较差，其他模型在拟合图中差别较小。

Figure 5. Fitting renderings of each model

图5. 各模型的拟合效果图

Figure 6. The fitting renderings of each model one day

图6. 各模型一天的拟合效果图

因此从表3来看，文章提出模型的MAPE较CNN-GRU、GRU-ATT、CNN-GRU-ATT模型分别提高8.35%、7.45%、9.14%、0.68%。在均方误差上有较大的降低，最少减低了18.54%，本文模型较好。

Table 3. Evaluation indicators of different models

表3. 不同模型的评价指标

5. 结论

本研究采用KCNN-GRU-ATT组合模型对短期交通流进行预测。在之前的文章中，已建立SVR、LSTM、GRU、CNN-GRU、GRU-ATT、CNN-GRU-ATT多个模型进行预测，这次加入K近邻算法，来检验监测点的空间相关性。通过不同K值的选取，对与目标监测点之间的相关性进行排序，最终选择最适合的K值，将数据输入本模型。实验结果显示，该模型较之前模型在均方误差上有较大降低，其他评价指标也表现更好。本文提出模型虽然预测效果较好，但考虑因素比较单一，之后的研究中可以加入气象数据进行分析。

NOTES

^*通讯作者。