突发公共卫生事件下城市应急物流配送中心选址问题

The Location Problem of Urban Emergency Logistics Distribution Center under Public Health Emergencies

摘要: 近年来，各类突发公共卫生事件突然爆发，尤其是重大传染性病毒，导致社会生活的各个方面都受到了极为严重的影响。在突发情况下，全国上下各地都面临着物资紧缺、配送速度慢等问题，为了将应急物资更快速更准确地配送到受灾区，建立城市应急物流配送中心意义重大，而应急物流配送中心的选址问题尤为关键。合理的选址不仅可以使物资快速而精准地配送到有需要的地方，解决灾区物资需求问题，还可以节省配送时间，缩短配送路线和配送费用，从而减少灾情带来的损失。本文基于k-means聚类算法和重心法建立选址模型，以湖北省为例，根据湖北省各地区的地理坐标、物资需求量等数据，代入模型进行实证研究，最终在湖北省选出合理的应急物流配送中心位置，从而验证了该模型的现实可行性。

Abstract: In recent years, the sudden outbreak of all kinds of public health emergencies, especially major infectious viruses, has caused extremely serious impact on all aspects of social life. In emergencies, all parts of the country are faced with shortages of materials, slow distribution and other problems. In order to deliver emergency supplies to the affected areas more quickly and accurately, it is of great significance to establish urban emergency logistics distribution centers, and the location of emergency logistics distribution centers is particularly critical. Reasonable site selection can not only quickly and accurately distribute materials to places in need, solve the problem of material demand in disaster areas, but also save distribution time, shorten distribution routes and distribution costs, so as to reduce the loss caused by the disaster. This paper establishes a location selection model based on k-means clustering algorithm and gravity center method. Taking Hubei Province as an example, this paper uses the geographical coordinates and material demand data of various regions in Hubei Province to conduct empirical research, and finally selects a reasonable location of emergency logistics distribution center in Hubei Province, thus verifying the realistic feasibility of this model.

1. 绪论

1.1. 研究背景

近年来，各种重大突发公共卫生事件频繁发生，给国家造成了不可估计的损失，这种情况下，应急物流就显得极为重要，其高效运作可以使救援工作高效进行，节省救援时间和成本。

重大公共卫生事件的爆发对全球人类生命安全、经济与社会进步等各个方面都会带来严重的影响，阻碍社会发展。近年来，在各类天灾人祸事件的抗击战中，各个主要受灾区医疗防控物资和生活物资频频告急，我们必须进行深刻反思，必须认识到当下我国以及全球应急物资保障体系还有很大的不足与改进空间，建立健全应急物资保障体系刻不容缓。

1.2. 研究目的和研究意义

1.2.1. 研究目的

《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》指出“提高快速调配和紧急运输能力”“加快建立储备充足、反应迅速、抗冲击能力强的应急物流体系” [1] 。

建立城市应急物流配送中心选址的模型，适用于城市灾害突然发生时的救援活动以及应急物资配送，根据实际受灾情况，选择最佳的应急物流配送中心的地点，从而降低灾情对人民生命安全和社会生活所带来的重大伤害和损失，该模型和求解方法可以应用于实际，为以后各种突发事件情况下的应急物流配送中心的选址问题提供依据，具有现实意义。

1.2.2. 研究意义

重大灾情下，各地区的物资需求量急剧增加，且总需求量极为庞大，包括医疗应急物资和生活物资等等，医疗物资有防护服、护目镜以及各种先进的医疗设备，生活物资包括蔬菜、水果和各种日常生活用品。城市应急物流配送中心的选址规划意义重大，对于节约配送成本、最大限度地减少城市区域内货物运输造成的交通拥堵至关重要，是保证物资快速及时精准供应的关键所在。

应急物流的概念在国内提出较晚，它是一种专门的应急后勤服务，主要是在严重的自然灾害或者重大社会性事件发生时，对各方面需求包括物资、资金、人员进行紧急调度与保障。应急物流与普通物流相比较而言，有着明显的区别，它要求对事件的发生快速做出反应，更多地考虑如何使灾害造成的损失最小和配送时间最短，关键性问题就是怎样将各个地区所需要的医疗和生活物资及时、精准地运送到受灾地区，其中最重要的一个关节就是配送，而物流配送中心的地理位置好坏与应急物资的配送质量直接相关。在对城市应急物流配送中心的选址问题进行研究时，要充分考虑各种因素，例如受灾严重程度、GDP变化幅度、物资需求数量、地理环境、政府政策等，将定量分析与定性分析相结合，对传统的模型和算法加以改进，从而最终确定应急物流配送中心建在何处是最合适的，这可以为受灾地区的救灾救援工作带来很多便捷，具有十分重要的意义 [2] 。

1.3. 城市应急物流配送中心选址研究现状

1.3.1. 国内研究现状

国内外研究者近年来兴起了对于应急物流以及配送中心的研究，取得了很多研究成果，也开发出了应急物流这一全新研究领域。

在如何对城市应急物流配送中心选址方面，严毅 [3] 等考虑到传统重心法的劣势，即理论距离与现实距离差距较大、运费计算不准确等问题，引入了非直线系数来对重心法进行改进，从而使得成本节约了百分之五点零六，为现实选址问题提供了参考意义。褚东亮 [4] 等在传统重心法的基础上，引入了禁忌搜索算法对选址问题进行了优化，并通过案例分析，将重心法与TSA相结合的计算结果与位置度量法、层次分析法相比较，从而验证了该算法的优势和可操作性。邸鸿喜 [5] 等研究了疫情下冷链物流配送中心选址问题，并充分考虑了新冠病毒感染这一要素，提出了新冠病毒感染风险系数，与CFIP模型结合，得到了最合理的选址结果。刘琳 [6] 等在对配送进行研究时，还考虑到了对生鲜产品新鲜度的要求和碳排放成本这两个因素，并建立了一种双层目标规划模型，结果相较于k-means聚类、遗传算法的平均成本分别改进了3.03%和1.22%。薛徳琴 [7] 等以江苏某电商企业物流配送为例，第一步用k均值算法对不同的协同配送区域进行划分，第二步运用层次分析法分别对不同的协同配送区域进行具体选址，最后用模糊综合评价法对选址结果进行评价。宗芳 [8] 等对“一带一路”沿线城市进行物流配送中心选址研究，考虑了众多经济因素，如投资运营成本、城市GDP等等，其建立了以效用最大化为目标、加入了熵权法TOPSIS的定量模型，该模型均衡了经济因素和非经济因素，最终得出促进沿线城市发展的最优方案。

1.3.2. 国外研究现状

Schilling [9] 等讨论了设施系统长期发展规划中的不确定性问题。在某些情况下，单一未来预测的高方差可以通过使用一组可选的未来情景来降低。通过仔细选择设施配置，规划者可以在收集额外信息和减少不确定性的同时，以很少或不牺牲的代价推迟未来设施地点的选择，这使得规划人员能够保持灵活性，以适应复杂和动态的环境。Caunhye [10] 等运用内容分析的方法，对应急物流优化模型进行了研究。灾难操作可以在灾难发生之前执行，也可以在灾难发生之后执行。灾前作业以短通知疏散、设施选址、物资预置为主，灾后作业以救灾物资分发、伤员运输为主。根据这些行动，其对三个方面进行了研究，分别是：设施选址、救援分发和伤员运输以及其他行动。对于前两部分，根据模型类型、决策、目标和约束条件对文献进行了结构和分析。最后，通过内容分析框架，找出几个研究空白，并提出未来的研究方向。Yi [11] 建立了多目标动态规划，但仍存在一些缺陷，其考虑了两种目标，包括物资配送速度最快和伤员救治延误时间最短，从而确定了一种应急物流选址模型，但实际灾情的发生却具有很大的不确定性和突然性。Horner [12] 等在进行配送中心位置选址问题的研究时，引入了GIS，但却忽视了各个地区的应急物资需求数量，缺少实际意义。

2. 城市应急物流配送中心选址方法分析

2.1. 配送中心选址常用方法

物流设施选址方法有很多种，其中常用的方法可以分为三类，即连续型模型选址法、离散型模型选址法以及综合因素评价法，每种类型都有其代表性的研究方法，且不同方法都有其优势和劣势。方法总结如下表1所示：

Table 1. Summary of common logistics facility location methods

表1. 常用物流设施选址方法总结

2.2. K-Means聚类方法

2.2.1. 聚类分析简述

聚类是对成员或要素进行归类和整理，即把研究要素按照某种分类标准，若某些要素在某种程度上比较类似，则将其集中于一组，聚类是一种挖掘数据内部结构的方法。在相同的集群或群组中，聚类对象的相似性更高。聚类的方法包括：系统聚类、图论聚类、有序样本聚类、聚类预测、动态聚类、模糊聚类等 [13] 。k均值聚类算法是当前学者普遍认为的最常用的分割聚类方法，它是给定一组数据点集和所需群集k，k是通常由使用者指定的，或者也可以通过建立算法等方法等找出，k均值聚类算法会根据一定的距离函数将资料分成k组，再通过不断地迭代，最后找到最佳的聚类分组。

2.2.2. K-Means聚类步骤

k-means聚类是本文对城市应急物流配送中心选址进行研究时的基础方法，k-means方法的基本步骤如下：

1) 给定聚类数为k，然后将聚类对象随机分为k组，再确定k个初始聚类中心。

2) 由于k-means聚类算法的聚类标准为距离，所以计算每个群组中的所有对象到该组簇心的欧氏距离(即直线距离)。此处，欧氏距离表示类似程度，聚类可以使得同一群组中的样本点具有较高的相似度，而不同群组间相似度低。欧氏距离的计算公式如下：

$D\left(x,C_i\right)=\sqrt{{\displaystyle \underset{j=1}{\overset{n}{\sum }}{\left(x_{ij}-C_i\right)}^2}}$ (1)

式中， $x_{ij}$ 代表第i个群组中的第j个聚类对象的坐标， $C_i$ 表示第i个群组的初始聚类中心，D表示每一簇中各个聚类要素到该组的对应的簇心的欧氏距离(即直线距离)。

3) 利用欧氏最小距离原理，将样本分布到最接近的群集，并以各簇内的平均值为新的群集中心。

4) 重复2)和3)，直到其结果不再发生改变或者到达最大迭代次数时，则簇心的位置基本上可以确定，并且聚类区的成员群也可以确认，不需要再继续进行迭代计算。

2.3. 重心法

2.3.1. 重心法简述

重心法常常用于选址决策问题，例如超市选址、学校选址以及应急物流配送中心的选址等等。重心法是把应急物流系统中的需求点看作一个在一定的平面上的目标，把各个点的需求和资源看作一个目标的质量，以目标系统的重心为最优的位置，并通过确定目标重心的方法来确定一个紧急物流设施的位置 [14] 。

2.3.2. 重心法假设条件

重心法的唯一决策标准是物资运输成本的最小化，如果可以使运输总成本最小，则该物流配送中心位置就是最佳的，可以应用的。所以在运用重心法进行选址决策时有以下三个假设条件：

一是由于各需求点散落分布，所以物资需求量不可能细化到每个点，所以它并不是实际的需求量，而是将某一相近区域内的需求量汇集，这样也方便配送。

二是物资配送的成本只体现在运输费用，而且重心法的目标函数中，运输费用仅仅体现在配送中心与需求点之间的距离，根据距离确定一个正比例关系，根据计算得出运输费用，却忽视了城市的交通运输状况等其他实际因素。在实际运输过程中，道路交通往往会出现各种难以预料到的状况，例如交通堵塞、有些路段红绿灯点较多、道路等级等，这些都能直接影响到运输成本 [15] 。

三是由于配送中心所处的地区不同，各种建设成本也会存在很大差异，如不同地区劳动力成本不同，土地费、建设费等也都不尽相同。所以在应用重心法选址时，默认假设不考虑这些因素带来的差异。

2.3.3. 重心法步骤

1) 假设各需求点的坐标为 $\left(x_i,y_i\right)$ ，应急物流配送中心的坐标为 $\left(x_0,y_0\right)$ ，用W表示配送中心到各点的运输费用，W的计算公式如下：

$W={\displaystyle \underset{i}{\overset{n}{\sum }}{w}_i}$ (2)

$w_i=r_i*q_i*d_i$ (3)

$d_i=k\sqrt{{\left(x_i-x_0\right)}^2+{\left(y_i-y_0\right)}^2}$ (4)

$k=\frac{两地间的实际公路里程}{两地间的欧氏距离}$ (5)

式中，W表示两地之间(即从配送中心到各需求)的总配送价格， $w_i$ 表示两地之间的配送价格，n表示受灾点的数量， $r_i$ 表示两地之间的配送费率， $d_i$ 表示两地之间的直线距离， $q_i$ 表示两地之间的配送量，k为修正因子，即两地间直线距离的修正系数。

2) 根据上式得

$W={\displaystyle \underset{i}{\overset{n}{\sum }}{r}_i*q_i*d_i}$ (6)

令 ${\partial W/\partial x}_0={\displaystyle \underset{i}{\overset{n}{\sum }}\left[r_i*q_i*\left(x_0-x_i\right)\right]}=0$ ， $\partial W/\partial y_0={\displaystyle \underset{i}{\overset{n}{\sum }}\left[r_i*q_i*\left(y_0-y_i\right)\right]}=0$ 得

$x_0=\left[{\displaystyle \underset{i}{\overset{n}{\sum }}{r}_i*q_i}*x_i/d_i\right]/\left[{\displaystyle \underset{i}{\overset{n}{\sum }}{r}_i*q_i/d_i}\right]$ (7)

$y_0=\left[{\displaystyle \underset{i}{\overset{n}{\sum }}{r}_i*q_i}*y_i/d_i\right]/\left[{\displaystyle \underset{i}{\overset{n}{\sum }}{r}_i*q_i/d_i}\right]$ (8)

对上面的结果进行迭代，求出最优解，迭代公式如下：

$x_{m+1}=\frac{{\displaystyle \underset{i\in I}{\sum }{r}_i*q_i*x_i/{\left[{\left(x_m+1-x_i\right)}^2+{\left(y_m-y_i\right)}^2\right]}^{1/2}}}{{\displaystyle \underset{i\in I}{\sum }{r}_i*q_i/{\left[{\left(x_m-x_i\right)}^2+{\left(y_m-y_i\right)}^2\right]}^{1/2}}}$ (9)

$y_{m+1}=\frac{{\displaystyle \underset{i\in I}{\sum }{r}_i*q_i*x_i/{\left[{\left(x_m+1-x_i\right)}^2+{\left(y_m-y_i\right)}^2\right]}^{1/2}}}{{\displaystyle \underset{i\in I}{\sum }{r}_i*q_i/{\left[{\left(x_m-x_i\right)}^2+{\left(y_m-y_i\right)}^2\right]}^{1/2}}}$ (10)

式中：m为表示迭代计算的次数，I为受灾区域所属的集合。

3) 迭代计算流程

(a) 随机确定一个配送中心的初始地点 $\left(x_{00},y_{00}\right)$ ；

(b) 将 $\left(x_{00},y_{00}\right)$ 的坐标数据代入式(4)中，计算各受灾点到初始配送中心坐标点的距离 $d_i$ ，再根据式(6)求得此时的总运输价格 $W_0$ ，即：

$d_i=k\sqrt{{\left(x_i-x_{00}\right)}^2+{\left(y_i-y_{00}\right)}^2}$

$W_0={\displaystyle \underset{i=1}{\overset{n}{\sum }}{r}_i*q_i*}k*\sqrt{{\left(x_i-x_{00}\right)}^2+{\left(y_i-y_{00}\right)}^2}$

(c) 将 $\left(x_{00},y_{00}\right)$ 代入式(9)和式(10)，得出首次迭代改进后的物流配送中心的坐标 $\left(x_{01},y_{01}\right)$ ，计算出此时新的总运输成本W₁，即：

$d_i=k\sqrt{{\left(x_i-x_{01}\right)}^2+{\left(y_i-y_{01}\right)}^2}$

$W_1={\displaystyle \underset{i=1}{\overset{n}{\sum }}{r}_i*q_i*}k*\sqrt{{\left(x_i-x_{01}\right)}^2+{\left(y_i-y_{01}\right)}^2}$

(d) 比较 $W_0$ 和 $W_1$ 的大小，如果 $W_1<W_0$ ，则返回第三步继续进行迭代，即把 $\left(x_{01},y_{01}\right)$ 代入式(9)和式(10)，得到第二次迭代改进后的配送中心的坐标 $\left(x_{02},y_{02}\right)$ ，如果 $W_1>W_0$ ，则说明 $\left(x_{00},y_{00}\right)$ 就是物流配送中心的最好的选址坐标；

(e) 继续进行迭代计算，直到出现 $W_{k+1}>W_k$ 为止，则 $\left(x_k,y_k\right)$ 即为配送中心选址坐标的最优解。

2.4. 基于K-Means聚类的重心法的改进

2.4.1. K-Means与重心法结合简述

由于传统重心法只适合单个的设施选址问题，而本文中需要建立多个城市应急物流配送中心，因此结合k均值聚类算法和重心法，首先利用k-means聚类分析算法对受灾点进行划分，然后依次在各个聚类区域内，分别采用重心法研究选址。通过两种方法结合，从而将“在一个区域内建多个配送中心的选址问题”转化为“多个区域内分别进行单一配送中心选址问题”，这样就对传统重心法进行了改进，发挥了两种方法的优势，使得模型具有一定的参考意义和借鉴价值，可以为现实中的选址问题提供解决思路。

2.4.2. K-Means与重心法结合流程图

将k-means聚类方法与传统重心法相结合，其大致步骤如下图1所示：

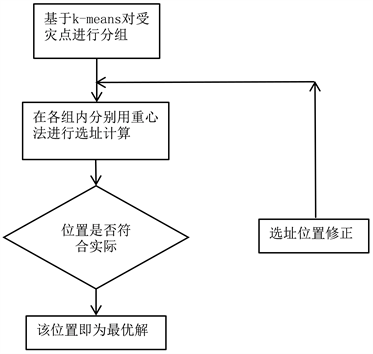
Figure 1. Solving model based on k-means’ center of gravity method

图1. 基于k-means的重心法求解模型

3. 实证研究

为了验证本文模型的可行性，本文选取2020年疫情时期受灾最严重的湖北省各区域作为实证研究对象。

3.1. 湖北省基本数据

湖北省位于中国的中部地区，东西南北方向分别与安徽省、重庆市、江西省、河南省接壤，北纬(N)范围为29˚01′53″至33˚6′47″，东经(E)范围为108˚21′42″至116˚07′50″。湖北省地域辽阔，总面积有18.59万平方千米。湖北省省会是武汉市，它有13个行政单位，其辖区内有12个地级市、1个自治州。

通过查阅高德地图，得到湖北省十七个地区的经纬度，即地理坐标。查阅各类官方数据以及权威媒体报道数据，收集到湖北省各区域2020年一季度的物资需求(包括新鲜蔬菜、医药等)，其中需求量为日均估值。如下面表2所示。

Table 2. Material demand and geographical coordinates of various regions of Hubei Province

表2. 湖北省各地区物资需求量及地理坐标

3.2. 实证分析步骤

3.2.1. K-Means聚类分析

本文计划在湖北省建立两个城市应急物流配送中心，即给定最佳聚类数k = 2。利用Matlab软件可计算聚类结果，如图2所示。图中红色坐标点表示聚类区域1，绿色坐标点表示聚类区域2，两个聚类区的质心坐标分别为(30.561, 114.02)和(31.23, 111.23)。

Figure 2. Matlab clustering results

图2. Matlab聚类结果

图3为轮廓系数，用来作为聚类性能的评估指标，轮廓系数的取值范围为[−1, 1]，取值越接近1说明聚类性能越好，相反，取值越接近−1则说明聚类性能越差。图3显示的轮廓系数均接近1，表示聚类效果较好。

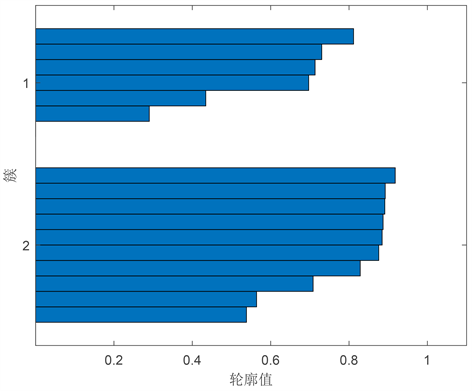
Figure 3. Cluster object outline values

图3. 聚类对象轮廓值

结果显示，武汉、黄石、鄂州、孝感、黄冈、咸宁、随州、仙桃、潜江、天门这十个地区为聚类区域1，余下的地区十堰、宜昌、襄阳、荆门、荆州、恩施、神农架林区这七个地区为聚类区域2。最终聚类分区结果如下表3所示：

Table 3. The final clustering result

表3. 最终聚类结果

3.2.2. 各聚类区内精确重心法选址

本研究中，即讨论疫情时期受灾的湖北省的配送中心选址问题，需要建立两个城市应急物流配送中心，分别位于聚类区域1和聚类区域2。经过前面的k均值聚类计算，已经确定了如何对湖北省的十七个地区进行分组，接下来要做的就是应用重心法分别在两个聚类区域内，选择合理的配送中心的位置，即把多设施选址问题转化成了单个设施的选址问题，解决起来更加方便。

根据本文第二章建立好的重心法模型，重心法需要考虑两个节点之间的运输距离、运输量、运输价格等数据。在本文中，为了便于计算，将所有节点之间的运输费率视为1，即生鲜农产品的配送费率为1元/t/km，医疗物资的配送费率为1元/万件/km。具体数据如下表4和表5所示：

Table 4. Transportation rates within cluster area 1

表4. 聚类区1内两地运输费率

Table 5. Transportation rates within cluster area 2

表5. 聚类区2内两地运输费率

根据上文建立的重心法模型，一步步计算出刚开始的物流配送中心坐标的xy值，x00 = 29.838，y00 = 114.05，将此结果以及其他所搜集到的数据代入公式③④⑤⑥，再进行一步一步迭代，直到总运费不再变少才停止，最终求得聚类区1内应急物流配送中心位置的最优解为x* = 30.60，y* = 114.31。在高德地图中查找此坐标点，发现该点位于武汉市解放大道，周围高速公路遍布广泛，交通便利，可以快速运输医疗物资和生鲜物资。

与上面求解聚类区1的配送中心最佳位置的计算过程相同，根据聚类区2的数据，代入重心法模型进行数次迭代计算后，最后结果为(31.04, 111.73)。查高德地图，发现该点位于湖北省宜昌市，此处远离山区、地势平坦、空旷，施工难度低，有利于加快基础设施的建设，缩短施工周期，为遭受灾情危害的地区迅速提供应急物资。用坐标图表示如下：图4中蓝色点代表湖北省各个地区，红色点代表两个配送中心选址。

Figure 4. Coordinate map of cities and distribution centers in Hubei Province

图4. 湖北省各市及配送中心坐标图

4. 总结

本文研究城市应急物流中心配送选址问题，以2020年初爆发新冠肺炎疫情时期的湖北省为例，首先指定了应急物流中心的个数，即建立2个物流配送中心。其次通过将k均值聚类算法与重心法相结合，建立了基于k-means聚类算法的改进重心法选址模型，并将实际数据代入建立的模型中。最终得出了两个配送中心的坐标位置，验证了所提出的模型和方法的正确性和优越性，可应用于以后城市突发事件或灾难时，为应急物流配送中心选址提供理论依据，具有一定的借鉴意义。当然，在现实问题决策中，还需要进一步结合实际，不能忽略现实因素，可以将模型提供的结果作为参考，这样才能保证所做决策更加地科学与合理。