多策略融合的鱼鹰算法

Osprey Optimization Algorithm with Multi-Strategy Fusion

摘要: 针对鱼鹰算法易于陷入局部最优、收敛速度慢等问题，本文提出了一种多策略融合的鱼鹰算法。在鱼鹰捕猎的阶段，引入黄金正弦策略，加快算法从搜索空间中收敛到可行解的速度；在鱼鹰移动猎物阶段，引入灰狼围攻策略，增加精英个体的引导作用，有效提高算法寻优精度；对适应度值排序倒数5只鱼鹰个体采用较差个体放逐策略，利用莱维飞行特性，增强算法跳出局部极值的能力。在MATLAB中利用12个基准测试函数与9个算法进行对比测试，并且将改进前后的鱼鹰算法应用在光伏电池参数估计中，实验结果表明了本文所提改进鱼鹰算法是一种寻优精度高、稳定性强的算法。

Abstract: Aiming at the problems that the osprey optimization algorithm is easy to fall into the local optimum and slow convergence, this paper proposes a multi-strategy fusion osprey optimization algorithm. In the stage of osprey hunting, the golden sine strategy is introduced to accelerate the convergence of the algorithm from the search space to a feasible solution; in the stage of osprey moving prey, the grey wolf siege strategy is introduced to increase the guiding role of the elite individuals and effectively improve the algorithm to find the optimal precision; the poorer individual banishment strategy is adopted for the bottom five osprey individuals in the order of fitness value, and the Levy flight characteristics are used to enhance the ability of the algorithm to jump out of the local optimal value. Twelve benchmark functions and nine algorithms are used in MATLAB for comparative testing, and the osprey optimization algorithms before and after the improvement are applied in the estimation of photovoltaic cell parameters, and the experimental results show that the improved osprey optimization algorithm proposed in this paper is a kind of algorithm with high accuracy of optimization search and high stability.

1. 引言

在各类先进技术不断被提出的当今，元启发式算法作为经典方案仍在各个领域有出色的表现。蒲公英优化算法(Dandelion Optimization, DO) [1] 、金豺优化算法(Golden Jackal Optimization, GJO) [2] 、蜜獾算法(Honey Badger Optimization Algorithm, HBA) [3] 、孔雀优化算法(Peafowl Optimization Algorithm, POA) [4] 、爬行动物搜索算法(Reptile Search Algorithm, RSA) [5] 、海马算法(Sea-horse Optimizer, SHO) [6] 等新的群智能算法层出不穷，图像分割 [7] 、路径规划 [8] 、资源调度 [9] 等应用场景也不断得到验证。

鱼鹰算法(Osprey Optimization Algorithm, OOA) [10] 是2023年由Mohammad D等受鱼鹰捕鱼行为启发提出的新群智能算法。鱼鹰是一种善于捕鱼的鸟类，其在水面上盘旋后俯冲将鱼抓出，然后将鱼带回巢穴或是在岸边吃掉。鱼鹰算法即模拟鱼鹰捕鱼的两个行为，具有较好的寻优精度，但是收敛速度较慢且易于陷入局部最优。文献 [11] 对象群领导者利用折射反向学习机制与柯西变异相融合进行扰动，有效提高算法跳出局部最优值的能力。文献 [12] 利用莱维飞行对侦察角色的麻雀个体位置移动方式进行改进，增强了算法的寻优能力。

因此，本文提出一种多策略融合的鱼鹰算法(Improved Osprey Optimization Algorithm, IOOA)。首先在鱼鹰算法的第一个阶段，引入黄金正弦策略加速鱼鹰在整个搜索空间内捕鱼，增强算法全局搜索的能力，提高收敛速度；其次在OOA的第二个阶段，引入灰狼围攻策略增强精英个体的引导力，提高算法寻优精度；最后引入较差个体放逐策略，对适应度值最差的5只鱼鹰进行莱维随机游走，提升种群多样性并且提高算法跳出局部最优值的能力。本文选取了12个基准测试函数以及9个算法进行对比，并且将IOOA和OOA应用在双二极管光伏电池等效模型的参数辨识中，实验结果表明了IOOA是一种寻优精度高、收敛速度快的算法。

2. 标准鱼鹰算法

鱼鹰算法旨在模拟鱼鹰发现水下鱼的位置后潜入水下捕捉并将捕到的鱼带到合适位置食用的行为。在发现食物并捕捉阶段，鱼鹰位置在整个搜索空间会发生较大变化。每个鱼鹰个体的位置作为一个候选解，这里将适应度值更好的位置设定为食物源的位置，鱼鹰的位置移动按照公式1进行。

$x_{i,j}^{new}=x_{i,j}+\text{rand}\times \left(S{F}_{i,j}-I\times x_{i,j}\right)$ (1)

其中 $S{F}_{i,j}$ 为所选择捕猎的鱼，rand为[0, 1]之间的随机数，I为{1, 2}之间随机数。 $x_{i,j}$ 为第i只鱼鹰个体的第j维位置， $x_{i,j}^{\text{new}}$ 是鱼鹰移动后得到的新位置。

在将鱼带到合适位置食用阶段，鱼鹰在当前位置附近较小范围内移动，开发阶段鱼鹰位置更新公式如下。

$x_{i,j}^{\text{new}}=x_{i,j}+\frac{lb+\text{rand}\times \left(ub-lb\right)}{t}$ (2)

其中ub是搜索空间的上界，lb是下界。t是当前迭代次数。每次比较移动前后位置的适应度值，将适应度值更好的作为新位置。

$x_i=\{\begin{array}{l}{x}_i^{\text{new}},{\text{iffit}}_i^{\text{new}}<{\text{fit}}_i\\ x_i,\text{else}\end{array}$ (3)

其中fit为适应度值，根据具体问题计算得到。

3. 改进鱼鹰算法

3.1. 黄金正弦策略

在标准OOA中，鱼鹰个体在当前位置的附近移动，仅仅依靠随着迭代次数增加，步长减小的方式完成局部开发，使得OOA局部开发能力不足。黄金正弦算法(Golden Sine Algorithm, Gold-SA) [13] 是一种由黄金分割系数和正弦函数引导的具有较强局部开发能力的算法。为了提高OOA的寻优精度，本文将黄金正弦策略引入捕食鱼的位置更新公式中。黄金正弦策略的数学建模如下，

$x_{i,j}^{\text{new}}=x_{i,j}\times \left|\sin \left(r_1\right)\right|-r_2\times \sin \left(r_1\right)\times \left|c_1\times S{F}_{i,j}-c_2\times x_{i,j}\right|$ (4)

其中 $r_1$ 为取值为 $\left[0,2\pi \right]$ 的随机数， $r_2$ 为 $\left[0,\pi \right]$ 之间的随机数， $c_1$ 和 $c_2$ 为收缩空间的因子，表达式如下，

$c_1=ag+b\left(1-g\right)$ (5)

$c_2=a\left(1-g\right)+bg$ (6)

其中a和b的初始值分别设定为 $-\pi$ 和 $\pi$ ，g为黄金分割率 $\frac{\sqrt{5}-1}{2}$ 。鱼鹰个体在收缩因子和正弦函数的引

导下能够快速精确找到搜索空间内的最优位置。

3.2. 灰狼围攻策略

在标准OOA中，开发阶段鱼鹰按照公式2找到更适合的位置进食，但是仅仅是在当前位置附近较小范围内移动，若当前位置所代表的鱼的位置对应的单一优秀个体不是全局最优个体，那么标准OOA中该阶段的移动方式就会增加陷入局部最优解的风险。因此，本文引入灰狼算法(Gray Walf Optimization, GWO) [14] 中多个优秀个体围攻的思想，在OOA中加入最优个体和次优个体的影响。灰狼围攻策略的数学建模如下，鱼鹰个体与最优个体和次优个体的距离分别为 $D_1$ 和 $D_2$

$D_1=\left|C\times \text{best}-X\right|$ (7)

$D_2=\left|C\times \text{sub}-X\right|$ (8)

其中best表示最优个体的位置，sub表示次优个体的位置。系数向量 $C=2r_3$ ， $r_3$ 是[0, 1]之间的随机数。受影响后的中间位置分别是 $X_1$ 和 $X_2$ 。

$X_1=\text{best}-A\times D_1$ (9)

$X_2=\text{sub}-A\times D_2$ (10)

其中A为系数向量，用公式11计算得到。

$A=2d{r}_4-d$ (11)

$d=2\left(1-\frac{t}{\text{max\_iter}}\right)$ (12)

其中max_iter是最大迭代次数， $r_4$ 是[0, 1]之间的随机数。受精英个体影响后的位置更新方式为：

$X^{\text{new}}=\frac{X_1+X_2}{2}$ (13)

3.3. 较差个体放逐策略

在标准OOA中，仅仅模拟了鱼鹰捕食鱼并将鱼带到合适位置食用的过程，对于鱼鹰种群中最优个体设定为鱼的位置，但是对于种群中较差的个体没有任何规定。这就导致适应度值较差的个体继续参与算法寻优，一定程度上造成计算资源的浪费。因此本文引入较差个体随机游走策略，对适应度值排序在最后5位的鱼鹰个体进行莱维随机游走 [15] ，增强算法跳出局部极值的能力。较差个体进行莱维随机游走的公式如下，

${\text{Ext}}_{t+1}={\text{Ext}}_t+\text{L <msup> e <mo> ′ </mo> </msup> vy}\left(\dim \right)\times {\text{Ext}}_t$ (14)

其中Ext表示较差个体位置，dim是维度，莱维飞行表达式如下，

$\text{L <msup> e <mo> ′ </mo> </msup> vy}\left(x\right)=0.01\times \frac{r_5\times \sigma }{{\left|r_6\right|}^{1/\beta }}$ (15)

$\sigma ={\left(\frac{\Gamma \left(1+\beta \right)+\sin \left(\frac{\pi \beta }{2}\right)}{\Gamma \left(\frac{1+\beta }{2}\right)\times \beta \times 2^{(\beta -1)/2}}\right)}^{1/\beta }$ (16)

其中 $r_5$ 、 $r_6$ 是[0, 1]之间的随机数， $\beta$ 一般取0.5。

3.4. IOOA主要步骤

本文改进IOOA主要步骤如下：

第一步：设置种群规模为N，最大迭代次数为max_iter，初始化种群。

第二步：计算鱼鹰个体适应度值并进行排序，分别设定前两名为最优个体和次优个体，设定排名最后的5位为较差个体。

第三步：模拟鱼鹰的位置识别及捕猎行为。选择适应度值小的位置为鱼的位置，按照公式4进行移动，利用黄金正弦策略快速搜索。

第四步：模拟鱼鹰的开发行为。根据公式13计算移动后的位置，利用最优个体和次优个体的影响因子提高算法寻优的准确度。

第五步：对排名后五位个体按照公式14进行放逐，增强算法摆脱局部极值的能力。

第六步：检查算法是否满足结束条件，若满足则结束循环，否则继续执行。

第七步：输出最优解。

改进IOOA的算法流程图如图1所示。

Figure 1. Flow chart of IOOA

图1. IOOA流程图

4. 算法性能测试

4.1. 基准函数测试实验

4.1.1. 基准函数

为了测试本文改进算法IOOA的性能，选取了 [16] 中的12个基准测试函数，其中F1-F5为单峰函数，F13是多峰函数，维度设定为30维，F14-F23为固定维度多峰函数。单峰函数只有一个峰值，求解简单，体现的是算法的全局搜索能力；多峰函数有多个峰值，算法容易收敛于局部峰值，因此求解复杂，体现算法应对局部峰值干扰的能力；而固定维度多峰函数设定更为复杂，因此求解更加困难。

4.1.2. 基本函数测试结果及分析

对比实验是验证算法有效性的常用方法。本文选取了蒲公英优化算法DO、金豺优化算法GJO、灰狼优化算法GWO、蜜獾算法HBA、孔雀优化算法POA、粒子群算法(Particle Swarm Optimization, PSO) [17] 、爬行动物搜索算法RSA、海马算法SHO、鲸鱼优化算法(Whale Optimization Algorithm, WOA) [18] 这9个包含经典算法以及近年提出的性能良好的算法作为对比算法进行实验。对比实验中设置的参数在表1中给出。

Table 1. Parameter settings

表1. 参数设置

实验环境为Windows 11系统，1.80GHz CPU，内存16GB，编程语言为MATLAB R2020b。为了避免偶然性对分析算法性能时造成较大偏差，实验将独立重复运行30次，将30次实验结果的平均值Mean和标准差Std记录在表2中，最优结果加粗表示。

Table 2. Results of comparative experiments

表2. 对比实验结果

分析表2数据可以发现，在选取的12个测试函数中，除了F15，本文改进算法IOOA的平均值均小于其余10个对比算法。在F15下IOOA排名第二，同样保持较高的寻优精度。在F21、F22、F23中，标准OOA就达到了很好的寻优结果，但是IOOA仍然超越了OOA。F21函数的理想最优结果是−10.1532，OOA和IOOA的寻优平均值均是理想结果，但是IOOA的标准差更小，说明在同等高精度的情况下IOOA的稳定性更强。F22的最优结果是−10.4028，IOOA取得−10.402851的平均值，而OOA的平均值是−10.402905；F23的最优结果是−10.5363，IOOA取得−10.536345，而OOA取得−10.536372，因此F22和F23中IOOA都是在平均值上相较OOA有着微弱优势。但在其他测试函数下IOOA相较OOA有明显优势，如F5、F13、F14、F15和F20，IOOA的寻优精度均超过OOA。因此IOOA是一种寻优能力强、适用范围广的算法。

将部分函数得到的收敛曲线在图2中给出，本文改进算法IOOA的收敛曲线用带有五角星的曲线表示，标准OOA用带有空心圆的曲线表示。

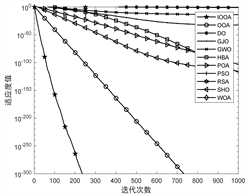
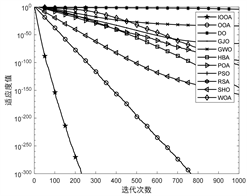
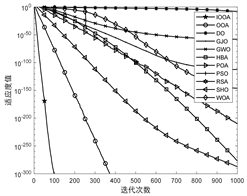
F1 F2 F4

F13 F14 F15F20 F22 F23

Figure 2. Convergence curves for benchmark test functions

图2. 基准测试函数收敛曲线

观察图2中F1、F2和F4的收敛曲线图可以看出，标准OOA算法在单峰函数下的收敛曲线在其他对比算法下方，说明了OOA算法自身就具有良好的性能，但IOOA曲线出现在OOA曲线更下方，证明了IOOA相比OOA有更高的寻优精度和收敛速度。在F13的收敛曲线图中，IOOA的曲线在所有对比算法曲线的下方，与其他算法曲线有明显区别，说明了IOOA在F13下的寻优效果相较于对比算法有明显优势。在F14的收敛曲线图中，可以看出POA、HBA、OOA以及IOOA的寻优效果较好，但是IOOA最先开始收敛并且收敛到了高精度结果，DO看似较晚开始收敛，但是同样达到了高精度寻优结果，结合表2数据可知，IOOA的标准差小于DO标准差，说明IOOA相较于DO算法更稳定。在F15图中，POA的收敛曲线在所有对比算法最下方，但是IOOA仅次于POA，同样表现出良好的性能。在F20的曲线图中，IOOA与OOA的收敛曲线差距明显，并且有几个算法收敛曲线在开始阶段出现在IOOA收敛曲线下方，但是结合表2数据，IOOA在第850次迭代就收敛到F20的最优值−3.2附近。在F22和F23的收敛曲线图中，相较于其他对比算法，IOOA和OOA的收敛曲线在最下方，说明OOA算法在处理这类较为复杂的问题时相比其他对比算法有着明显优势，结合表2数据分析，IOOA和OOA在F22和F23下的寻优效果差距虽然不大，但是IOOA相较OOA更接近函数的理想最优结果。各个对比算法在测试函数下的收敛曲线图直观验证了IOOA是一种收敛速度快、寻优精度高的算法。

4.1.3. 秩和检验

为了更准确的对比各个算法的寻优效果，Wilcoxon秩和检验是常用的统计检验方法 [19] 。一般来说，秩和检验标准设置为0.05，即当秩和检验结果小于0.05的时候，说明改进算法相较于对比算法有显著优势，其他情况说明没有显著优势。各个对比算法相较于IOOA的Wilcoxon秩和检验结果记录在表3中。

Table 3. Results of the Wilcoxon rank sum test

表3. Wilcoxon秩和检验结果

表3中可以观察到，包含OOA在内的10个对比算法在12个基准测试函数下的秩和检验结果均远小于标准值0.05，说明本文改进IOOA相较于对比算法有着显著性优势。进一步验证了IOOA的有效性和竞争性。

4.2. 双二极管光伏电池参数辨识应用

除了测试算法的基本性能，还需要检验算法实际应用的能力。光伏电池的参数辨识是群智能算法的一个典型应用场景，其中双二极管光伏电池模型(Double Diode Equivalent Model, DDM) [20] 有着电路模型相对简单、参数精度要求高的特点。DDM中所需辨识的7个参数分别是光生电流 $I_{ph}$ 、扩散电流 $I_{sd1}$ 、饱和电流 $I_{sd2}$ 、串联电阻 $R_s$ 、并联电阻 $R_{sh}$ 、扩散二极管理想因子 $n_1$ 和复合二极管理想因子 $n_2$ ，这7个参数的边界在表4中给出。

Table 4. Boundaries of DDM parameters to be measured

表4. DDM待测参数边界

实际的电压值和电流值数据在 [21] 中可以找到，在标准温度25℃下进行实验，将标准OOA和改进IOOA进行DDM参数辨识得到的结果记录在表5中，将均方根误差(Root Mean Square Error, RMSE)作为参数辨识准确性的评价指标，最优结果加粗表示。

Table 5. Results of DDM parameter identification

表5. DDM参数辨识结果

表5中可以明显看出IOOA的RMSE小于OOA的RMSE，说明了改进IOOA的参数辨识准确度更高。为了更直观的对比改进前后算法的参数辨识效果，将拟合的I-V和P-V特性曲线在图3中给出，其中实际数据用虚线表示，OOA估计的数据用空心圆表示，IOOA估计得到的数据用五角星表示。

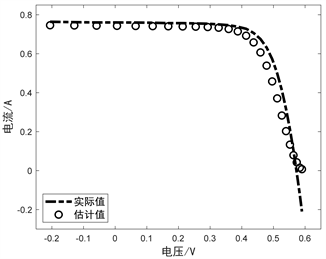
OOA的I-V曲线 OOA的P-V曲线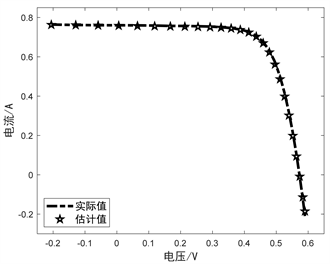 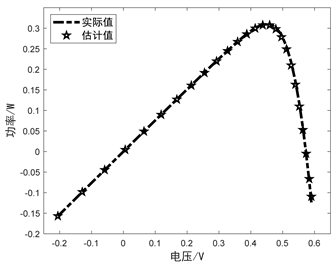IOOA的I-V曲线 IOOA的P-V曲线

Figure 3. I-V and P-V characteristic curves of the algorithm before and after improvement for DDM parameter identification

图3. 改进前后算法对DDM参数辨识的I-V和P-V特性曲线

观察图3曲线可以看出，标准OOA虽然基本拟合出实际数据的形状，但是有明显误差，而IOOA得到的曲线与实际数据拟合程度高，说明IOOA进行DDM参数辨识的效果更好、准确度更高。

5. 总结

本文针对标准OOA算法寻优精度不高、易于陷入局部最优等问题，提出了改进的IOOA。在鱼鹰进行位置识别及捕猎阶段，引入黄金正弦策略，利用正弦函数快速收缩在被选鱼的位置附近，加快OOA全局搜索的速度；在将鱼带到合适位置的开发阶段，引入灰狼围攻策略，利用最优个体和次优个体的影响力选择精确度高的开发位置；每次迭代将适应度值排名后5位个体重新释放到搜索空间中进行莱维随机游走，增强算法跳出局部最优值的能力。在算法性能测试中选用12个基准测试函数进行实验，包含单峰函数、多峰函数以及固定维多峰函数，并选用9个性能良好的对比算法，实验结果表明IOOA是一种有竞争力、稳定性强的算法。将改进前后的鱼鹰算法应用于双二极管光伏电池模型的参数辨识中，均方根误差以及拟合的I-V、P-V曲线均证明了IOOA相较于标准OOA改进效果明显，是一种寻优精度高的算法。