基于基本面分析的量化投资——以券商行业为例

Quantitative Investment Based on Fundamental Analysis—Taking Securities Industry as Examples

摘要: 本文先是对基本面分析以及量化投资的背景进行介绍，然后对基本面分析以及量化投资的概念模型进行阐述。在分析层面先是对我国券商行业的几个宏观指标做出了研究。通过基本面分析的量化投资理论，找取了A股市场的所有50支券商股票，先通过数据预处理选出38只券商股票，然后借助R、SPSS、MATLAB和LINGO软件对券商2020年1月1日至2021年12月31日的所有真实数据先进行月平均处理，并对下个月的数据进行预测，之后对预测值先进行基于熵权法的Topsis算法，得出其中综合得分较好的5支股票。再通过均值–方差模型画出有效边界图，并给出其中一种最优的投资权重组合及收益。

Abstract: This paper first introduces the background of fundamental analysis and quantitative investment, and then expounds the conceptual model of fundamental analysis and quantitative investment. At the level of analysis, several macro indicators of China’s securities industry are studied. Based on the quantitative investment theory of fundamental analysis, all 50 securities stocks in the A-share market are selected, and 38 securities stocks are selected through data preprocessing. Then, all re-al data of securities companies from January 1, 2020 to December 31, 2021 are processed on a monthly average basis with the help of R, SPSS, MATLAB and LINGO software. Then, Topsis algo-rithm based on entropy weight method is used to predict the predicted value, and 5 stocks with good comprehensive scores are obtained. Then the effective boundary graph is drawn by means of mean-variance model, and one of the optimal investment weight portfolios and returns are given.

1. 引言

1.1. 课题背景

基本面量化投资(一种新的量化与价值相结合的智能量化投资方法)，其关键是通过研究证券基本面和超额收益率间的关联。通过基本面研究和定量投资相互促进，使基本面投资成为实现价值投资的现代手段。基本面定量的选股模式，是对企业财务指标、证券市场状况、行业情况等各种因素综合加以衡量，从而利用数学手段合理地解释并估计证券市场的异常收益情况。当我们将基本面分析结果纳入量化模型框架，将有助于对股票投资以及股票组合作出更全面、更可靠的研究结果。其优势在于：首先，基本面分析为定量模型的建立奠定了坚实的逻辑基础；第二，量化投资分析可以从大量历史数据中获得更可靠的统计规则；第三，基本面分析考虑公司未来的增长，选择相关因素，并根据历史数据检验因素的有效性；第四，基本面投资可以深入分析投资组合的绩效及其影响因素。

1.2. 研究意义

从表面上看，基本面分析指的是对宏观经济和政治数据的综合分析。事实上，它的目的是判断金融市场的未来趋势。基本面分析主要适用于周期长、证券市场相对成熟、预测精度要求低的地区的证券价格预测。基本面分析以证券的内在价值为基础，关注影响证券价格和趋势的各种因素，从而决定投资哪些证券以及何时购买。

本文正是在这样的背景下，研究者期望从证券公司的投资状况中获得的利益，对其进行基本面量化投资研究。通过对量化模型的分析，获得最佳的量化投资战略，为证券公司未来的量化投资提出了一些宝贵的建议。一方面，以量化为基础的投资组合，在试图引进基本面分析的过程中，往往会出现一些问题。量化投资的专家往往把专门技术看作是一个重要的区别。因此，在进行量化基本面时，他们常常缺少相关的经验，从而造成了失误；而在另一种情况下，对那些注重于量化的公司而言，模式的解释同样是一个棘手的问题。模型的可解释性可比单纯的建立一个量化模型要困难的多。因此，基本面与量化的融合是一个非常重要的课题，寻找二者的相似性，进行更深一步的剖析。

1.3. 国内外研究现状

1.3.1. 国外研究现状

Gordon和Shapiro [1] 基于未来现金流量的折现，研究了基于公司当前股息和公司基本面的股息增长计量，并论证了基本面分析的合理性，但该分析模型对高增长公司的预测精度仍然较低。

Feltham G和Ohlson J [2] 提出了非常收益模型，考虑了股息的折现和资产价值的剩余收益，并对当前的会计基础和公司未来的收益进行了调查，以研究并得出结论。

在此基础上，Rappaport [3] 提出了贴现现金流模型。贴现现金流模型结合了公司的基本因素、增长和未来创造现金流的能力，通过当前现金流预测股票价值，更好地研究股票。

Lee和E.C. [4] 提出，基本面量化投资是一种新的投资方法，将定量投资(机器驱动)和价值投资(人力驱动)结合起来。它是近年来备受关注的一种智能量化投资方法。基本面定量投资的核心是分析股票基本面因素与风险溢价之间的关系，或者通过分析准确预测股票收益。他们通常通过对市场异常现象的研究来分析学术研究中的基本因素，并分析能够提供超额回报的公司的特征。

Feng等 [5] 使用lasso方法测量因素对资产定价的贡献，发现利润因素和投资因素比之前发现的数百个因素具有更显著的统计解释力。

1.3.2. 国内研究现状

张然和汪荣飞 [6] 基本面量化投资是量化投资和价值投资的深度融合，其核心因素是超额收益与股票的基本面因素之间的关系。基本面投资与数量投资的互补性使基本面数量投资成为现代价值投资手段。同时机器学习算法是一种能够有效识别异常因素与超额收益之间复杂模式的算法，它的投资策略比传统的线性算法和所有单一因素都能获得更好的投资性能。

李斌 [7] 基于A股市场的96个异常因素，采用预测组合算法、lasso(套索)回归、岭回归和偏最小二乘回归等12种机器学习算法，系统比较了机器学习驱动模型和线性回归模型在中国市场的实证表现，并从机器学习的角度检验了模型中异常因素的重要性，研究将基本面量化投资引入机器学习将有助于促进人工智能、机器学习、经济学和管理学的交叉融合。

王伦 [8] 引入了gcforest算法，建立了基于gcforest的股票投资市场多因素量化投资策略。

周隽和何鹏飞 [9] 基于从价值因素、盈利能力因素、经营能力因素、增长能力因素、偿债能力因素和质量因素六个维度中选择的候选因素，最终通过模糊c均值聚类(FCM)算法筛选出影响因素，建立多因素模型。

侯晓辉和王博 [10] 对基本面量化投资进行了梳理，探讨了基本面分析、量化投资理论与实践的发展以及基本面量化的内涵。然后介绍了其重要的理论基础和测量方法，系统梳理了相关实证研究进展，并提出了未来的研究展望，为该领域的后续研究提供有力的参考。

1.4. 研究方法

1) 时间序列滑动平均法

时间序列的滑动平均法。该方法采用按顺序逐期增减数据来求取移动平均数，从而剔除偶然性变化影响，先查明新事物变化，而后再加以预测的方法。

2) 基于熵权法的Topsis算法评价方法

熵权法：信息熵是对信息的不确定性程度进行的一个衡量。信息量就越大，不确定性就越小，熵值也就越小，因此基于信息熵的特点，既可以利用计算熵值来确定某个事件的随机程度，也可以利用信息熵值来确定一个指数的离散程度，当指数的离散程度越大时，该指数对事件综合评价的影响程度也越大。

Topsis法：对于给定有限个的评价对象与理想化目标的接近程度进行排列顺序的方法，是对现有的评价对象进行评价好坏的一种算法。

基于熵权的Topsis算法评价方法：我们在执行评价中在Topsis算法的基础之上引入熵权来确定决策矩阵的各项指标的权重。

3) 均值–方差模型

均值–方差模型又称马科维茨模型 [11] ，是马科维茨在1952年提出的投资组合优化模型。该投资组合理论主要是用均值和方差来表述股票的收益和风险这两个关键因素对投资的影响。而其中的均值是指股票组合的平均期望收益率。而方差则是指投资组合的回报率的平均值，它既反映了实际回报率与均值之间的离散性，也说明了投资组合所面临的风险。

2. 数据来源与处理

2.1. 数据准备

本文选择A股市场中券商板块50家券商公司2020年1月1日至2021年12月31日财务报表的数据，实验数据均来自wind数据库。由于全部数据量很大，以下给出数据的部分截图，以表1申万宏源公司2020年1月的流通市值、市盈率、市盈率(静态)、基本每股收益、每股净资产、beta值6个指标为例给出数据。

Table 1. Index data of Shen Wan Hongyuan in January 2020

表1. 申万宏源2020年1月指标数据图

2.2. 数据预处理

缺失值处理

由于股票在选择期内未上市等原因导致数据缺失，并且由于每家上市公司公布的财务数据之间存在差异，或者说收集者在收集数据时存在遗漏都可能会在导出原始数据后出现缺失值。因此，我们需要补充填写缺失的数据值。我们主要通过以下方式处理数据的缺失值：

1) 删除缺失值：主要有简单删除法和加权法。简单删除法是处理缺失值的最简单方法之一。简单的删除方法主要是是直接删除缺失的样本。若存在数据缺失的问题，只需删除少量样本即可实现，那么这种方法是最有效的。但当缺失值的类型为不完全随机缺失时，则需要通过加权数据来减少数据的偏差。

本文采用直接删除缺失值的方法，由于财达证券、中金公司、中泰证券、国联证券和中银证券的流通市值存在大量缺失不易于进行补充，所以需要直接删去这5家公司；由于华西证券、长城证券、华林证券、中信建设、天风证券、红塔证券、南京证券的beta值存在大量缺失不易于进行补充，所以直接删去这12家公司。最后将这些证券公司删除，将样本从50家公司缩小为38家。

2) 用可能的值来插值补充缺失值：这个方法的主要思想是通过使用方法来用最可能的值插补缺失值，这可能比删除所有数据会减少信息损失。所以对于部分缺失值较少的公司(如华安证券等)，我们可以采用拉格朗日插值算法来填充缺失的数据，步骤如下：

①给定k + 1个取值点：

$\left(x_0,y_0\right),\cdots ,\left(x_k,y_k\right)$ ，

其中 $x_i$ 对应自变量， $y_i$ 对应函数位置所在的值。

②假设任意给定的两个 $x_i$ 互不相同，应该使用拉格朗日插值公式得到拉格朗日插值多项式为：

$L\left(x\right)={\displaystyle \underset{j=1}{\overset{k}{\sum }}{y}_i{l}_i\left(x\right)}$ ，

$l_i\left(x\right)={\displaystyle \underset{i=0,i\ne j}{\overset{k}{\prod }}\frac{x-x_i}{x_j-x_i}}=\frac{x-x_0}{x_j-x_0}\cdots \frac{x-x_{j-1}}{x_j-x_{j-1}}\frac{x-x_{j+1}}{x_j-x_{j+1}}\cdots \frac{x-x_k}{x_j-x_k}$ ，

本文对于缺失值也采用了拉格朗日插值法来填充缺失的数据，以下图1是基于拉格朗日插值算法对华安证券的基本每股收益进行拟合，我们发现插入的数值符合曲线曲度，准确性较高。

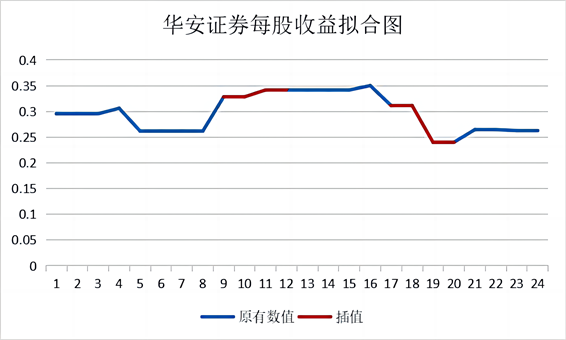
Figure 1. Fitting chart of basic earnings per share of Huaan Securities

图1. 华安证券基本每股收益拟合图

2.3. 指标选取

我们在筛选股票进行基本面分析的量化投资，必须对基本面的财务指标进行选取，必须较好的分析券商板块每个公司的各项指标。

借鉴于周隽，何鹏飞 [9] 在文章中通过研究将资料的市盈率、市净率、市销率、总资产收益率、净资产收益率、销售净利率、固定资产比例、总资产增长率、流通市值、基本每股收益等十六个候选因子先划分到价值水平因子、盈利水平因子、运营水平因子、成长水平因子、偿债水平因子五个维度再进行模糊C均值聚类分析。

本文选取了财务指标数据包括这50只券商股票的流通市值、市盈率、市盈率(静态)、基本每股收益、每股净资产、beta值这6个原始财务数据作为基本面指标进行分析。选用上述指标是因为这是企业进行基本面分析常用的指标，这上述6个指标之间的联系各自能解释大部分情况下企业的财务状况。在不考虑其他因素影响情况下，每股收益越高的同时风险越小的话，收益率就越高。基本面指标的解释详见下表2。

Table 2. Fundamental index table

表2. 基本面指标表

3. 基于基本面分析的选股策略

3.1. 基于时间序列滑动平均法分析

因为基本面指标的“过去”和“现在”都可能存在统计依赖关系，所以，我们采取了基于时间序列滑动平均模型对50家证券公司未来一个月6个基本面指标的数据进行预测，希望通过预测值来更好地代表长时间的真实值。

该部分借鉴于周游 [12] 对金融时间序列进行分析，使用滑动平均算法来对金融时间序列进行计算滑动平均线交叉点的收益率和命中率的分析。

以下是进行时间序列滑动平均法的过程：

设定时间序列的观测序列为 $y_1,y_2,\cdots ,y_t$ ，设定移动平均的项数N。一次简单移动平均值计算公式为：

$M_t^{\left(1\right)}=\frac{1}{N}\left(y_t+y_{t-1}+\cdots +y_{t-N+1}\right)=M_{t-1}^{\left(1\right)}+\frac{1}{N}\left(y_t-y_{t-N}\right)$ ，

基于搜集的数据运用SPSS建立时间序列滑动平均模型，得出38只券商股票基本每股收益、每股净资产、市盈率、市盈率(静态)、流通市值、beta值的预测结果。其中，由于预测时前五项指标值越大越好，而beta值越小越好，所以为将beta值变为正向指标，我们取beta值的倒数进行预测出2022年1月的数据，如下表3。

表3为38只券商股票基本每股收益、每股净资产、市盈率、市盈率(静态)、流通市值、beta值的预测结果，我们使用六个指标的预测结果，利用熵权法，为后文选出优质券商股票以建立投资组合模型提供数据支撑。

Table 3. General forecast table

表3. 总预测表

3.2. 基于熵权法的Topsis算法分析

根据3.1.部分所预测的六个指标值，利用熵权法的Topsis算法，计算得到38家券商股票的综合得分，从而选取综合得分较高的股票。这一部分借鉴于邵毅明和钟颖等 [13] 选用神经网络等5种模型，分别对路段未来时刻短时交通流进行预测，构建基于熵权法的Topsis算法的短时交通流综合评价模型，对各预测模型的预测性能进行综合评判。

3.2.1. 建模步骤

本部分我将基于熵权法的Topsis算法的理论步骤进行介绍。

第一步 构建原始矩阵并归一化：

1) 假设有n个需要进行评价的券商，m个评价的基本面指标构成的正向化矩阵X如下：

$X=\left(\begin{array}{ccc}{x}_{11}& \dots & x_{1n}\\ ⋮& \ddots & ⋮\\ x_{m1}& \dots & x_{mn}\end{array}\right)$ ，

2) 采用最大–最小标准化的方法对各个指标进行标准化处理，其中 $x_{ij}$ 代表第i个券商公司的第j个基本面指标值。

$x_{ij}=\frac{x_{ij}-\min \left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}}{\max \left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}-\min \left\{x_{1j},x_{2j},\cdots ,x_{nj}\right\}}$ ，

第二步 计算熵值：

1) 求出m个评价指标的值

$e_j=-\frac{1}{\ln n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{p}_{ij}}\ln \left(p_{ij}\right)\left(j=1,2,3,\cdots ,m\right)$ ，

n是券商个数，计算第j项指标下第i个样本所占比重作为运算中的概率 $p_{ij}$

2) 计算信息效用值 $d_j$

$d_j=1-e_j$ ，

3) 对信息效用值进行归一化处理得到每个指标的熵权 $w_j$

$w_j=\frac{d_j}{{\displaystyle \underset{j=1}{\overset{n}{\sum }}{d}_j}}\left(j=1,2,3,\cdots ,m\right)$ ，

第三步 寻找最优、最劣解：

1) 确定正负最优、劣理想解

$\begin{array}{l}{V}^{+}=\left\{\underset{1\le i\le m}{\max }V|i=1,2,\cdots ,m\right\}\\ V^{-}=\left\{\underset{1\le i\le m}{\min }V|i=1,2,\cdots ,m\right\}\end{array}$

第四步 欧式距离计算：

2) 计算评价指标与正负理想解的欧式距离

$D_i^{+}=\sqrt{{\displaystyle \underset{j=1}{\overset{m}{\sum }}\left(V_{ij}^{+}-V_j^{+}\right)}}\left(i=1,2,\cdots ,m\right)$ ，

第五步 计算相对最优评分：

3) 得出方案最优评分T

$T=\frac{D^{-}}{D^{+}+D^{-}}$ ，

最终的评分是用一个样本到最优解和最劣解的欧式距离来决定的，其中样本到最优解的距离记为 $D^{+}$ ，到最劣解的距离记为 $D^{-}$ ，最终的方案最优评分为T。

3.2.2. 运行结果

该部分我们通过R3.6.3运用forecost包分析，使用各基本面指标预测数据对38家券商股票基于熵权法的Topsis的综合得分，最终结果如表4所示。

Table 4. Comprehensive score table

表4. 综合得分表

最终将全部券商公司的综合得分进行降序排序，并选取排名前五公司，分别是中信证券、广发证券、国信证券、东方证券、东兴证券。

4. 基于均值–方差模型的量化投资

根据3.2部分得到综合得分最高的五只股票，利用均值–方差模型将对这五支券商股票进行分析，给出这五只股票的量化投资组合。

4.1. 原理简介

本部分运用均值–方差模型来对股票进行投资，这种投资是在综合考虑了投资的风险和收益的情况下进行的。这一部分借鉴于佐拉 [11] 通过对澳大利亚4家公司选取了12个月的时间序列股票数据的分析，由两种股票作为风险资产的投资组合的风险和预期收益，基于均值–方差模型得到符合各自风险承受能力的最优投资组合。

该部分先介绍均值方差模型的公式，模型公式如下：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{w}_i}E\left(R_i\right)=E\left(R_p\right),$ (1)

${\sigma }_p^2={\displaystyle \underset{i=1}{\overset{n}{\sum }}{w}_i^2{\sigma }_i^2}+2{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{n}{\sum }}{w}_i{w}_j{\sigma }_{ij}}},$ (2)

$E\left(R_p\right)$ 是投资组合的期望收益； $w_i$ 是资产i在投资组合中的权重； $E\left(R_i\right)$ 是资产i期望收益； ${\sigma }_p^2$ 是投资组合的方差； ${\sigma }_i^2$ 是资产i的方差， ${\sigma }_i$ 则是资产i的标准差； $w_i$ 是资产i在投资组合中的权重， $w_j$ 是资产j在投资组合中的权重； ${\sigma }_{ij}$ 是资产i和资产j的协方差，它等于相关系数 ${\rho }_{ij}$ 和资产i和资产j的标准差的乘积。

4.2. 运行结果

通过得到2022年1月的股价均值，我们求得这5家证券公司的收益率(每投入一元可得到的收益)，该收益率即为模型中所需要求得的均值：

Table 5. Rate of return table

表5. 收益率表

并且我们需要计算得出基于均值–方差模型的这5家券商股票的收益率的方差、标准差、协方差，结果如下表6、表7。

利用上表5、表6、表7求出的均值、标准差、协方差，并结合均值–方差模型的理论可知，我们需要实现的目标便是收益率(均值)最大化且风险(方差)最小化。为此，我们运用4.1中的公式(1)、(2)建立多目标规划模型：

Table 6. Table of variance and standard deviation of rate of return

表6. 收益率的方差和标准差表

Table 7. Covariance table of yield

表7. 收益率的协方差表

公式(1)中的 $E\left(R_i\right)$ 为该目标函数中的 $x_i$ ， $E\left(R_p\right)$ 为下述目标函数的 $Z_2$ 公式(2)中 ${\sigma }_p^2$ 为下述目标函数的 $Z_1$ 。

目标函数： $\{\begin{array}{l}Min{Z}_1={\displaystyle \underset{i=1}{\overset{5}{\sum }}{\displaystyle \underset{j=1}{\overset{5}{\sum }}{w}_i{w}_j{\sigma }_{ij}}}\\ Max{Z}_2={\displaystyle \underset{i=1}{\overset{5}{\sum }}{w}_i{x}_i}\end{array}$ ，

约束条件： $\{\begin{array}{l}{\displaystyle \underset{i=1}{\overset{5}{\sum }}{w}_i=1}\\ 0\le w_i\le 1\end{array}$ ，

$Z_1$ 是投资组合的方差，用来代表投资组合的风险； $Z_2$ 是投资组合的均值，用来代表组合的收益；

$x_i$ 是第i只证券的收益率； $w_i$ 或 $w_j$ 是第i支或第j支证券的投资权重； ${\sigma }_{ij}$ 是第i支和第j支证券的协方差。

通过LINGO和MATLAB软件，我们求出5家券商股票投资组合权重的最优解并画出有效最优解并画出有效前沿图，如下图2所示：

Figure 2. Effective frontier graph

图2. 有效前沿图

如图2所示，有效前沿图的横轴代表了标准差即风险，纵轴表示均值即收益，有效前沿线上的每一点都代表了一种最佳的组合。当我们给定收益时能够确定风险；而给定风险水平也能够确定收益。比如在有效前沿图中标出的该点为风险为9%时，收益率为6.5%。

同时我们也求出了5家券商股票投资组合权重的最优解，如下表8所示：

Table 8. Weight table of stocks

表8. 股票权重表

最终，在5家证券公司收益率保持当前水平下，我们得出其中一种在均值–方差模型下的最优投资组合，可以按照表8的权重分配我们的投资。

4.3. 投资预测

4.3.1. 预测结果

根据熵权法得出的综合得分最高的五家公司——中信证券、广发证券、国信证券、东方证券、东兴证券，进行均值–方差模型的量化投资预测得出投资的权重和收益率，得出当投资47.87%的国信证券和52.13%的东兴证券时收益最大。

基于熵权法和均值方差模型进行量化投资时，假设在2022年1月初投入100万元资金，分别购买47.87万元的国信证券和52.13万元的东兴证券，则 $Z_2=0.0810\times 47.87+0.0406\times 52.13=\text{5}\text{.9939}$ 万元为我们所得的收益。

4.3.2. 现实比较

但在真实情况下，在同花顺软件中查询得2022年1月国信证券的收益率为−6.45%，而2022年1月东兴证券的收益率为−9.03%，求得收益为 $Z=-0.0645\times 47.87-0.0903\times 52.13=-7.794954$ 万元。

真实收益为5.9939万元，而预测收益为−7.794954万元，两者之间相差较大，究其误差原因，是因为市场是一个各种因素综合影响下的市场，在均值–方差模型下我们只考虑了股票的收益和风险，所以得出了预测较好的收益，但是真实情况下，市场受到政策和投资者心理波动的影响。2022年1月中国A股市场持续低迷，上证指数月初为3651.89点即为该月的最高点，月末3356.56点即为该月的最低点，1月上证指数震荡下行。在大盘影响下，该月券商板块在月初就开始破位下行，临近下旬一度向上尝试反弹但尝试失败，1月下旬至春节前出现持续下跌的情况，最终以最低价月收盘，1月券商板块的跌幅明显，呈现普跌情形，且板块中的大多数股票的下跌幅度较为明显。而我们所进行投资的国信证券1月涨跌幅为−6.45%，东兴证券的涨跌幅为−9.03%，跌幅较为明显，整个投资市场的情绪较差也导致了跌幅的加剧，导致了我们真实值与预测值的误差。

5. 结论与思考

5.1. 研究结论

本文以券商行业作为基本面量化投资研究的目标，先通过分析2010年至2020年我国券商行业的发展趋势，比较分析营业总收入、净利润等指标的发展趋势，发现2010年至2020年间券商行业的发展先向下后向上，总体呈现一个增长趋势。在投资环境较差的当下，配置一些券商资产不失为抵御投资风险的良策。

本文选取了基本面分析的6个指标，找取了A股市场的所有50支券商股票，先通过对数据的缺失直接进行删失和拉格朗日法填补值进行数据的预处理，筛选出38只券商股票，然后对券商2020年1月1日至2021年12月31日的所有真实数据先进行月平均处理，并对下个月的数据进行预测，之后对预测值先进行基于熵权法的Topsis算法，根据该算法得出了其中综合得分排名前五支的股票——中信证券、广发证券、国信证券、东方证券、东兴证券。再通过均值–方差模型，在共同考虑衡量收益和风险的情况下画出有效边界图，有效边界曲线上的点都是最优的解，通过分析给出对五只股票的其中一种最优的投资权重组合，当我们在2022年1月投资100万元时，我们将100万元的47.87%投入国信证券，52.13%投入到东兴证券会得到最佳的收益5.9939万元。

5.2. 研究思考

基于上述我本篇对基本面分析的量化投资的研究，得出了基于熵权法的Topsis算法和均值–方差模型下的我对量化投资组合及收益的结论，为量化投资的研究给出了基本面分析的研究，但在分析中我有以下思考：

1) 运用量化投资理论和股票基本面分析可以选出一些符合投资条件的券商，但股票市场具有不确定性，经过基本面分析的量化模型也存在风险，因此选出的股票不一定能得到预期的回报。每个券商个股所面对的非系统风险可以通过建立投资组合进行规避。

2) 量化投资的建立离不开基本面分析和技术分析。但在长线的投资中，我们更需要注重基本面的分析。我们要敬畏市场，但不必过于恐惧市场的风险。进行投资是一个十分漫长的过程，希望在这个过程中投资者能够不盲从、不跟风，坚持自己的策略进行投资。

3) 指标值的收集由于收集者的失误可能会导致数据的缺失或者是数据的错打漏打都会导致关键信息的缺失。同时本文采用直接删除缺失值的方法有些过于莽撞，也会导致结论的局限性，我们在下次处理数据时需要更加谨慎。

4) 对于不同风险和收益偏好的投资者，我们需要给出不同形式的投资组合，需要修改风险和收益在模型中的权重参数。