1. 引言
《常微分方程》作为数学分析的分支,是数学与应用数学专业的一门基础课程。它伴随着微积分理论产生与发展,是自然科学和其他科学领域重要的研究工具之一,已成为处理数学理论联系实际问题的有力方法和途径 [1] [2] [3] [4] 。它同时是定性理论、稳定性理论、动力系统等后继领域研究的基础。常微分方程还与其他学科或领域结合出现各种新的分支,如控制论,种群生态学、分支理论、脉冲微分方程等。常微分方程所探究的模型通常来自于物理、力学、社会、生物、化学及气象等自然世界,师范生学习常微分方程课程对学生学科素养提升有着潜在价值。学生通过学习该模块化课程,使其具备解决问题、自主学习与研究、创新的能力。《常微分方程》模块化课堂教学贯穿以学生为中心理念,运用多种教学策略进行教学设计和实施,积极有效组织学生参与校内外实践教学活动 [5] [6] [7] [8] 。
2. 专业认证理念与专业培养现状
《常微分方程》不仅是中学代数的延拓,也是现代数学的基础。然而由于本课程概念多,内容抽象,理论性强,思维方式独特,学生普遍反映难学。说它难学有课程的客观原因,同时也有学生的主观因素。
然而,目前很多高校数学与应用数学师范专业的常微分方程与专业认证理念,在构建模块化教学内容结构体系的过程中,还有一定的偏差和脱节。
3. 课程教学模块化
微分方程模块化课程采取混合式学习(B-Learning)的策略,通过多样化的活动和评价为核心。利用网络线上课程和电子资源,传统线下课堂和线上网络的优势,实施以教师为主导的课堂教学活动和以学生为主体的网络学习活动,突出常微分课程课堂教学的“学生为中心”地位。教师可尝试如下教学循环结构设计(图1),使教学任务实施有章可循。结合基于混合式学习的教学模式和教学理念,不仅加强了学生的学科素养的提升,学生在教育实践中善于发现问题、及时反思,了解数学教学研究方法,具有初步的数学教学研究能力。同时为学生树立创新发展的意识,具有一定的教学创新能力,帮助学生学会创造性地解决学习和教育教学实践中遇到的真实问题。
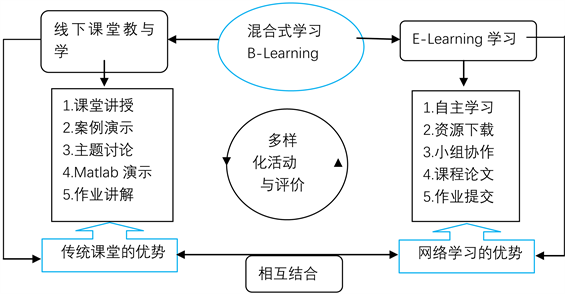
Figure 1. Teaching cycle structure design flow chart
图1. 教学循环结构设计流程图
4. 线上线下教学融合化
根据数学与应用数学(师范)人才培养目标定位,在教学方式上,按照常微分方程“理论模块 + 应用案例 + 软件模拟”的模式授课,将网络资源课程与线下课堂教学相结合,分块组织实施教学计划,形成较为特色的课堂教学体系。在实践体系上,通过课程实践,在明确的任务驱动下,充分利用Matlab等软件工具以及混合式教学MOOC,使学生在“学中做、做中学”,逐步培养学生自主学习的意识和应用实践能力。同时,在考核方式上,可探索建立多元化、过程性与期末考核相结合评价模式,强调以任务驱动,督促学生课前、课中、课后各环节完成目标任务,进一步全面提高学生的思维能力、动手能力和创新能力。
5. 实施过程目标化
结合我校数学与应用数学专业应用型人才培养目标,确立《常微分方程》课程的功能和建设目标,本着“在学中做、在做中学”的思想,积极挖掘课程思政元素,力争做到思政理念入课程、有考核。围绕学生创新能力的培养和综合素质的提高,力争为数学与应用数学专业相关课程建设提供如下改革和建设的范例。
1) 融入思政元素,充分挖掘课程内容中的思政元素,优化课程标准,让学生在掌握《常微分方程》基础理论、数学分析方法和模型数值模拟应用的同时,深刻理解微分方程与动力系统领域创新、建模与演化规律预测等思想。探索《常微分方程》网络教学资源与课堂教学相结合的教学方式。
2) 以学生为中心,强化能力导向,以任务驱动方式构建项目化实践教学体系。把课堂讲授与实验操作相结合,经典的解的存在唯一性理论与动力系统理论发展现状相结合,培养学生的学习兴趣;重基础,重原理,重应用,培养学生的认知能力。通过课程的模型背景、建模过程、数值模拟以及模型预测等,激发学生的使用现代数学工具的模拟兴趣;通过常微分方程课程设计、创新研究计划和毕业论文等,培养学生动手操作的实践能力。
3) 改革考核方式,融入思政考核内容,建设贯穿教学过程的过程性考核评价体系。完善的考核评价体系必须以充分调动学生学习主动性为根本,建立多元化、过程性考核评价模式是促进教学质量提升的保障,因此在考核模式设计上要科学合理,特别是对思政教育效果考核评价方面要制定相应方案,课程总评成绩除了包括平时成绩、实验成绩和期末成绩外,还应该包括教学过程中的项目试验完成情况、网络平台学习情况等方面的考核。
6. 建模思想操作化
现在的教学多数采用传统的教学模式,虽然多数教师采用多媒体方式授课,常微分方程中建模思想既有理论证明也有结合理论解与数值模拟结果对实际现象给出合理的解释,从而提高学生的学习兴趣。
本文以欧拉方程数值解为例,将常微分方程课程线上与线下相融合。对该教学任务作可如下的安排:事先,布置求解微分方程
在讲授求解该微分方程问题之前,同时让学生检查计算机上Matlab软件能否正常运行,并通过网络资源查找求解常微分方程的三种算法,独立读懂三种算法的程序代码。教师可安排二至三名学生通过Matlab软件和多媒体展示布置的作业任务,并将完成情况纳入该课程的考核评价。教师板书该微分方程求解步骤和详细过程,给出该方程的解
。
然后,引入新课,介绍欧拉方法的数值解内容。在讲解过程中,同时让学生分别利用Matlab软件进行数值解模拟。将学生氛围五组,每组分别为使用欧拉方法、改进欧拉方法、2阶龙格–库塔方法、4阶龙格–库塔方法计算方程
的解,设定统一步长为
。学生独立完成后,学生分组展示,教师并与教材给出演示图进行比较进行逐一点评。
7. 小结
本文以《常微分方程》课程模块教学为例,在师范认证背景下,探索案例教学穿插到抽象的理论基础课程的教学过程。引入探究式、提问互动式、案例讨论、问题学习等方法进行组合授课,既有利于学生形成正确的数学观,立足学科思想和方法,拓宽专业视野,也有利于培养学生熟练应用信息技术和数学软件,以及在教育实践中善于发现问题、解决问题的能力。这为探索常微分方程教学与其他课程教学改革提供有意义的参考范例。
基金项目
本文受安徽省省级大学生创新创业训练计划项目资助(S202314098038)。
NOTES
*通讯作者。