耦合物理场下的电机振动噪声分析

Analysis of Motor Vibration and Noise in Coupled Physical Fields

摘要: 本文通过有限元仿真技术在物理耦合场中进行电机振动，噪声的仿真分析。首先通过Maxwell进行电机在转速1500 r/min得工况下，仿真得出电磁力密度，经过转换得到频域下得电磁激振力。接着用ANSYS进行模态分析，确定得电机定子的一阶固有频率为1632.5 Hz，并求出前六阶固有频率以及模态振型。然后将电磁激振力作为远程载荷结合模态分析，进行了谐响应分析，得出一阶固有频率的振幅。最后通过噪声分析，确定了在频率为2000 Hz时的噪声为30.723 dBA。本文的仿真工作为电机减振降噪的设计优化提供了完整的分析流程。

Abstract: This article uses finite element simulation technology to simulate and analyze motor vibration and noise in a physically coupled field. Firstly, Maxwell was used to simulate the electromagnetic force density of the motor at a speed of 1500 r/min, and the electromagnetic excitation force in the fre-quency domain was obtained through conversion. Next, modal analysis was conducted using ANSYS to determine the first-order natural frequency of the motor stator as 1632.5 Hz, and the first six natural frequencies and modal shapes were calculated. Then, the electromagnetic excitation force was used as a remote load combined with modal analysis to perform harmonic response analysis and obtain the amplitude of the first natural frequency. Finally, through noise analysis, it was de-termined that the noise at a frequency of 2000 Hz was 30.723 dBA. The simulation work in this ar-ticle provides a complete analysis process for the design optimization of motor vibration and noise reduction.

1. 引言

永磁电机是世界上出现的第一种电机产品，是包括汽车等多领域在内的核心部件。随着近几年的集成电路技术，电子元器件和微型计算机技术的快速发展。永磁电机也凭借其功率大，高效率，体积小，低耗能等优势迎来了属于它的时代。无论是航天领域，农用领域，军工领域等都得到了广泛的应用，也取得了一些成果。随着电机的快速发展，人们对于电机的要求也越来越高 [1] 。不仅仅对于电机要求功率高，转速高，也对于电机的振动，噪声等方面的优化越来越重要 [2] 。而对于电机的设计优化来说，在电机设计量产之前对电机进行振动，噪声分析，在源头控制住振动，噪声的产生，是非常重要的。

针对电机的振动问题，国内外学者提出了众多优化方案，并做了大量深入的研究。Wang等人进行了复杂径向电磁力下的电机动建模，讨论了转子偏心对振动的影响，并开发了定转子振动响应的预编程程序。廖晓文运用外差法，对电机的转子磁极所输出信号的相位差进行了改进，并进行了实验验证 [3] 。Sandra M. Castano通过分析切换策略对径向力波形的影响，运用调整导通角的方法来降低电磁径向力高变化率，从而降低开关磁阻电机的振动 [4] 。张自有通过对滑模观测器和切换函数进行改进，有效地减小了电机运行所产生的高频抖振。郭建英针对电机的转矩脉动问题，提出谐波注入的研究新方法，在Matlab/Simulink模块中建立了电机控制系统，并对此方法实验验证了其可靠性 [5] 。吴伟等人针对电机的转速不同步问题，提出了一种基于新型偏差耦合结构的非奇异终端模糊滑膜控制策略，并在控制结构上引入PID速度补偿器，有效提高了系统的鲁棒性与稳态性能 [6] 。姜富宽基于转子分段提出了一种抑制转矩的齿槽新结构，建立了电机转矩解析模型，并对齿宽进行优化组合，经有限元仿真和实验验证表明该方法对电机的转矩脉动抑制有显著作用 [7] 。

本文通过有限元的方法对永磁同步电机中的定子进行了振动，噪声仿真分析。由此从源头进行减振，降噪，提出优化方案。本文首先在ANSYS旗下的Maxwell软件中搭建了电机主要部件定转子的二维平面图，并通过求解器求解出电机转动时产生的径向电磁力。然后对定子部分进行了模态分析，得到定子的固有频率。然后将Maxwell中分析的径向电磁力作为远程载荷导入到定子部分的谐响应分析中，结合模态分析部分，进行谐响应分析。最后将谐响应分析的结果最为远程载荷导入到Harmonic Respone模块进行了谐波声学分析。

2. 振动，噪声仿真

2.1. 电磁分析

本文通过Solidworks设计了电机的定转子模型如图1，图2所示。在此模型上进行定子的振动，噪声仿真。本例设计的电机转子部分是24个定子槽。

Figure 1. 3D part drawing of motor stator and rotor

图1. 电机定转子三维零件图

Figure 2. 2D plan view of motor stator and rotor

图2. 电机定转子二维平面图

电磁分析模块通过Maxwell软件中的RMxprt模块进行电机定转子二维模型的绘制。在此模块绘制需要给定一定的电机定转子相关的参数。本次仿真分析的对象具体参数见表1。

Table 1. Maxwell simulation analysis parameter table

表1. Maxwell仿真分析参数表

本文通过瞬态求解，得到了气隙中随时间变化的转矩，结果如图3所示。由数据可以得某一时刻的电机二维平面磁场图如图4所示。由于旋转机械电机随着时间，空间的变化气隙磁密是不同的，根据后处理结果的电机定转子之间的气隙磁密如图5所示。

Figure 3. Torque over time graph

图3. 转矩随时间变化图

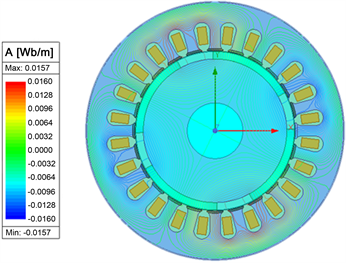
Figure 4. Air gap magnetic field line distribution diagram

图4. 气隙磁场线分布图

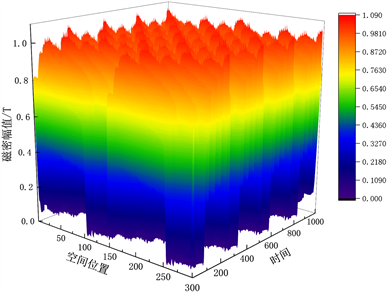
Figure 5. Distribution map of air gap magnetic density over time and space

图5. 气隙磁密随时间，空间变化分布图

由图3的结果可知，在一定的电机转速条件下，转矩随时间是周期性变化。由图4可知，磁场整体的变化，并且可以看到磁场是对称分布的。由图5可知，气隙磁密随时间空间变化图。

2.2. 模态分析

2.2.1. 模态分析理论基础

本文考虑无阻尼条件下多自由度结构的模态分析，以两自由度为例。不考虑阻尼，结构的运动微分方程矩阵形式可以表示为：

$M\ddot{x}+Kx=f$

式中，M，K分别为结构的质量矩阵和刚度矩阵；x，f分别为结构相应及结构的外部激励向量。设两自由度结构初始向量状态为零，对其运动微分方程做傅里叶变换可得

$\left(K-w^{2}M\right)X\left(w\right)=F(\; w\; )$

得其阻抗矩阵为

$Z\left(w\right)=K-w^{2}M=\left[\begin{array}{cc}{k}_1-w^2{m}_1& -k_1\\ -k_1& k_1+k_2-w^2{m}_2\end{array}\right]$

两自由度结构得频响函数为二阶矩阵，可由其阻抗矩阵得逆矩阵计算可得

$\left[\begin{array}{cc}{H}_{11}\left(w\right)& H_{12}\left(w\right)\\ H_{21}\left(w\right)& H_{22}\left(w\right)\end{array}\right]={\left(K-w^{2}M\right)}^{-1}=\frac{\left[\begin{array}{cc}{k}_1+k_2-w^2{m}_2& k_1\\ k_1& k_1-w^2{m}_1\end{array}\right]}{\left(k_1+k_2-w^2{m}_2\right)\left(k_1-w^2{m}_1\right)-k_1^2}$

频响函数矩阵中任意元素 $H_{lp}\left(w\right)$ 表示l响应与p点激励之间得频响函数，当 $l=p$ 时称为原点频响函数，当 $l\ne p$ 时称为跨点频响函数。由于结构得质量矩阵和刚度矩阵均对称，易得知频响函数矩阵也为对称矩阵。由频响函数矩阵即可确定系统固有特性。

2.2.2. 模态分析仿真

将Maxwell 2D图形转换为Maxwell 3D，然后进行定子的模态分析。Maxwell 3D图形如图6所示。本文采用的是34定子槽的定子进行绕组设置。

Figure 6. 3D model diagram of stator

图6. 定子3D模型图

对于本文的永磁同步电机采用的模型，在进行模态分析是，认为是同一种不锈钢材料。其密度是7.85 × 10⁶ kg/mm³，杨氏模量是2 × 10⁵ MPa，泊松比是0.3。将材料赋给模型并进行模态计算。作为此模型的永磁同步电机定子的固有频率如表2所示。

Table 2. Natural frequency of motor stator

表2. 电机定子固有频率

各阶的定子变形如图7所示。

Figure 7. The first six modal shapes

图7. 前六阶模态振型

在ANSYS计算过程中，对于自由模态下的固有频率实际前6阶为刚体模态。所以从第七阶开始取为第一阶，同时因为模型具有对称性，会有相近的阶数，其实为同一阶。

2.3. 谐响应分析

提取Maxwell中定子齿部受到的电磁激振力，作为谐响应分析的载荷。如图8所示，以及谐响应分析远程载荷力和力矩如图9所示。

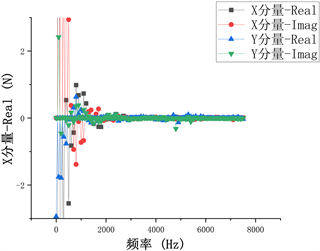
Figure 8. Data graph of stator tooth excitation force score

图8. 定子齿激振力得分量数据图

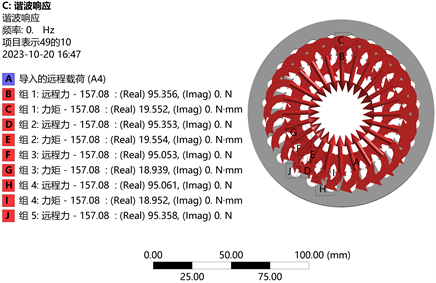
Figure 9. Harmonic response analysis of remote loads

图9. 谐响应分析远程载荷

由图7可知，定子齿部受到的力和力矩在x，y，z方向都表现出了在低频情况下的幅值比较大，随着频率的增加，力和力矩在三个方向上的分量都逐渐区域稳定。

由图9可知力和力矩分布的方向，大概可以了解定子的转动方向。

通过谐响应分析可以得到振幅随频率变化，和相位角随频率变化图，如图10所示。

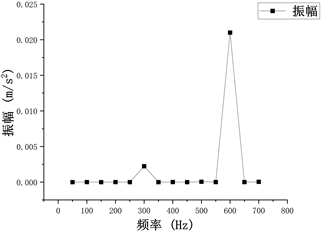
Figure 10. Harmonic response analysis frequency response function diagram

图10. 谐响应分析频响函数图

2.4. 噪声分析

为了计算电机在受迫振动下的电机噪声在空气域中的分布情况，将谐响应分析的计算结果做激励远程导入到Harmonic Acoustics模块建立耦合，进行电机的噪声分析。综合电磁分析，模态分析，谐响应分析。设置一个环状的空气域，作为声学区域。通过分析求解可以得到如图所示的声压级图和频率响应如图11，图12所示。

由图11可以看出噪声分布具有对称性，并且随着空气域的慢慢扩大，噪声也早逐渐的减弱，这也符合空气振动遭遇空气摩擦，逐渐减弱。由图12可知，随着频率的增加，噪声也逐渐增加，在达到一定的频率时，逐渐收敛。

Figure 11. 3D noise distribution map

图11. 三维噪声分布图

Figure 12. Noise frequency response diagram

图12. 噪声频响图

3. 结论

本文针对永磁同步电机进行的振动噪声仿真分析。由上述仿真分析，可得出结果。

(1) 电机电磁激振力分析过程中，主要提取电磁体对定子齿产生的电磁激振力。结果显示磁感应密度最大为0.0157 Wb/m，最小为−0.016 Wb/m。将此磁感应密度值转换为电磁激振力，作为远程载荷，进行谐响应分析。

(2) 由模态分析仿真结果可知，一阶固有频率在1632.5 Hz，模态振型为定子横向拉伸。二阶固有频率为2948 Hz，模态振型为定子两端向2个方向拉伸。三阶固有频率为4342 Hz，模态振型为定子整体向三个方向拉伸。在此基础上可以进行一定优化设计，提高一阶固有频率。

(3) 由谐响应分析可知，在一阶固有频率，二阶固有频率出，会出现很大的幅值。表示，振动频率在此阶段内会产生很大的振动。将谐响应分析得到结果作为噪声分析的远程载荷。

(4) 由噪声场分析可知，当振动频率在2000 Hz时，会产生最大30.723 dBA的噪声。在此基础上可以进行减噪设计。