1. 引言
近年来,计算机软件已经渗透到几乎所有领域,成为现代社会的重要组成部分,深刻地改变了人们的生活方式、工作方式和社会互动。但是,一旦计算机软件发生故障将会导致严重后果,从数据丢失和业务中断到安全泄露和法律责任。例如:2020年8月9日,美国国土安全部的一些系统经历了持续数小时的故障。这次故障影响了海关和边境保护局的运营,造成长时间的边境延误。2021年3月2日,微软Exchange服务器发生了漏洞,导致数千个组织的电子邮件数据泄露和被攻击。这些软件失效案例不胜枚举,因此,研究软件可靠性保障软件系统正常运行、提高软件质量是现代软件开发和维护过程中不可或缺的一部分。
软件可靠性增长模型(software reliability and growth model, SRGM) [1] [2] [3] 是软件工程领域的关键工具,用于建立数学模型描述和预测软件系统可靠性的变化趋势。此类模型在软件可靠性的评测、保证、测试资源优化和发布策略 [4] [5] 研究中具有重要作用。当前最常用的参数模型是非齐次泊松过程(non-homogeneous Poisson process, NHPP) [6] [7] 类软件可靠性增长模型。最先提出的NHPP类模型是G-O模型 [8] ,其后改进得到了Delayed S-shaped和Inflection S-shaped等经典模型。建立NHPP类软件可靠性增长模型首先需要提出基本假设,建立数学模型,然后基于具体数据利用最小二乘估计或最大似然估计求解模型中的参数,得到具体的拟合函数。传统的参数化软件可靠性模型存在许多缺点,这些缺点与其不切实际的假设、环境依赖的适用性和可疑的预测性直接相关。
非参数模型无需预先假设函数的具体形式,而是基于数据集进行估计。与参数化软件可靠性增长模型相比,非参数模型有着更强的适应性且拟合精度较高。Hao [9] 等引入一种对数风险函数的惩罚非参数最大似然估计,用于分析右删失数据,并使用光滑样条平滑估计。Yu [10] 等通过建立分类回归模型来表征交通流与不同时间点的关系,并通过具有光滑样条的负二项式模型识别不同的交通流模式。Suk [11] 等首先提出分段线性模型,其中数据的时域被划分为连续的阶段,并且在每个阶段拟合一条单独的线性回归线,其中惩罚样条模型通过引入惩罚项来实现拟合度和平滑度之间的平衡。Liu [12] 等提出了一种贝叶斯时变系数模型来评估多类型循环事件的强度的时间分布,该模型使用贝叶斯惩罚样条获得时变系数和基线强度的平滑估计值。Dohi [13] 等考虑了数据驱动的软件可靠性评估方法,可以在不完全的故障计数分布知识下为软件可靠性预测提供有用的概率信息。Choudhary [14] 等进行了软件可靠性预测建模:参数化和非参数化建模的比较,评估并比较了2个参数和2个非参数软件可靠性增长模型在3个真实数据集上软件故障的准确性。Dharmasena [15] 等采用基于具有核平滑的局部多项式建模的非参数方法来进行SRGM建模,并提供数值示例对模型进行评估比较。
综上所述,关于软件可靠性模型的研究主要分为参数模型和非参数模型。本文利用非参数模型中的光滑样条回归模型对开源软件累计故障数进行研究。其余部分主要内容如下:第二节主要介绍了基于光滑样条回归的软件可靠性模型;第三节针对真实数据集进行案例分析;第四节根据分析结果得出结论。
2. 基于光滑样条回归的软件可靠性模型
2.1. 非参数回归模型
非参数回归 [16] [17] [18] 是统计学研究的一个热门方向,有着广泛的应用前景,受到国内外学者的广泛关注。由于失效数据没有固定的分布以及可靠性模型没有具体的函数形式,因此本文选择非参数回归模型进行累计失效数的拟合和预测。
给定一组累计失效数
,若想研究软件失效数Y与时间变量X之间的关系,可将其表示为非参数回归模型的形式:
(1)
其中
为未知光滑函数,假定随机误差
。
令
,
,
,则模型(1)可写成:
(2)
2.2. 光滑样条回归模型
光滑样条回归 [19] 是一种常见的非参数回归模型,可以用于拟合开源软件以月为单位的累计失效数。由于光滑样条回归软件可靠性模型是由数据驱动模型,因此具有较强的稳健性和适应性。其在软件可靠性回归拟合中的思想是使用样条在每个时间段内拟合一个方程,然后在时间点处将这些分段曲线光滑的连接起来。光滑样条回归的目的是在保持模型光滑性的同时,尽量减小观测数据与模型之间的残差。即需要满足残差平方和最小准则:
(3)
其中:
为时间,
为累计失效数,
为回归方程的拟合值。由于光滑样条的节点数较多,会导致模型出现过拟合现象,因此需要在(3)式的基础上引入一个惩罚项,故判断准则为:
(4)
其中,
是一个非负的调节参数,
,主要是为了控制回归函数的拟合优度和光滑程度之间的平衡,其值过小会导致过拟合,过大会出现有偏估计。
为惩罚项,其目的是为了提高拟合曲线的光滑程度。
是
的二阶导数,表示拟合函数
的弯曲程度,
值越大,曲线波动越厉害,曲线也就越粗糙。接下来本文将以自然三次样条为例,展示光滑样条回归模型对累计失效数估计值的显示表达式。
2.3. 自然三次样条
在
上有一组软件失效时间
,
,如果f满足以下两个条件:
1) f在区间
上都是三次多项式;
2) f在时间节点
处的一阶、二阶导数都连续,且在
上也连续。
那么称f为三次样条函数。此外,如果满足
,那么f为自然三次样条,即f在
是线性的。自然三次样条的形式为:
(5)
令
,
,根据自然三次样条的边界条件可得
。接下来先引入两个带状矩阵Q、R:
(6)
其中元素
,
,
,
,当
时,
。
(7)
其中元素
,
,其中当
时,
。
易知矩阵R为严格正定矩阵,令
,由f和
确定自然三次样条的充要条件是
,则
(8)
因此,(4)式可表示为矩阵形式为
(9)
对(9)式关于f求导,令其导数为零可使得上式最小化,故得f的估计为
(10)
回归函数f对累计故障数的拟合程度可归结于参数
的取值。
3. 案例分析
为了验证与比较模型的性能,本文基于真实数据集对GO模型、DSS模型、ISS模型以及光滑样条回归模型进行对比分析。
3.1. 失效数据
Tomcat服务器是一个由Apache软件基金会开发和维护的轻量级、开源的Web应用服务器,通常在中小型系统以及访问并发较低的场景中广泛使用。Tomcat服务器通常与其他组件和工具一起使用,如Apache HTTP服务器、数据库、应用程序框架等,以构建完整的Web应用程序堆栈。本文所需的故障数据来源于Tomcat服务器版本3-11的用户缺陷跟踪系统(http://bz.apache.org/bugzilla/)。
Tomcat的主要数据字段有Auth、Catalina、Cluster、EL、Jasper和Manager等。本文以月为单位进行数据整合,提取了从2010年1月到2023年8月期间检测到的故障数(共164组数据),失效数据见表1。

Table 1. Tomcat3-11 failure data
表1. Tomcat3-11失效数据
3.2. 模型评估准则
为了比较模型的性能,本文选择以下指标进行衡量:MSE,AIC。
1) 均方误差(Mean Squared Error,简称MSE)是一种常用的评估指标,用于衡量估计值与实际观测值之间的差异,从而量化模型的拟合精度。数学上,MSE可以表示为:
(11)
2) 赤池信息量准则(AIC) [20] 是一种模型选择的统计指标。它用于平衡模型的拟合优度和复杂性,以便选择最适合的模型。在不同模型选择时,优先使用具有较小AIC值的模型。AIC的计算公式为:
(12)
其中:L是模型的似然函数值,k是模型中的参数数量,也称模型的复杂度。当误差服从正态分布时,AIC可以表示为:
(13)
其中:m是样本容量,RSS是残差平方和。
3.3. 模型性能对比分析
本文基于表1中Tomcat的真实数据集,利用最小二乘估计求解出了NHPP类软件可靠性增长模型的参数估计结果,进而得到模型的具体表达式。模型的参数估计结果以及拟合优度结果如表2所示。从表中可以看出光滑样条回归模型的MSE (10.6977)和AIC (397.0549)这两个拟合度评估指标比其他3个可靠性模型的值都要小。从以上评价指标的数值可以看出,对于本文的失效数据,光滑样条回归的拟合效果最好,而DSS模型的拟合效果最差。

Table 2. Least squares estimation of parameters and model comparison results
表2. 参数的最小二乘估计和模型比较结果
各模型的失效拟合图如图1所示。从图中可以看出,光滑样条回归模型对累计故障数拟合效果较好。

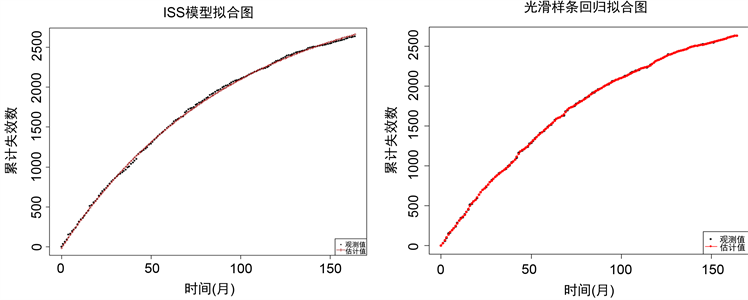
Figure 1. Cumulative failure count fits for each model
图1. 各模型的累计失效数拟合图
图2为四种模型的拟合对比图,整体分析可知,光滑样条回归模型的拟合效果要优于NHPP类软件可靠性增长模型。这也说明由于非参数回归不需要前提假设且对数据集进行分段拟合,因此非参数回归相比于参数回归有着更强的稳健性和适应性。
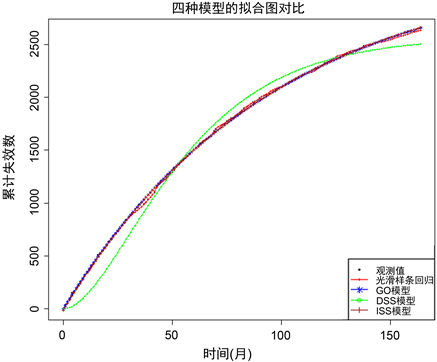
Figure 2. Comparison of fits for four different models
图2. 四种模型的拟合对比
3.4. 预测性能对比分析
为了分析模型的预测性能,本文绘制了四种模型的相对误差(RE)曲线。其中RE曲线越趋近于0,预测性能越好;大于0是正向预测;小于0是负向预测。
使用Tomcat数据集进行的预测揭示了模型对未来测试性能的描述和对未来累计故障数的检测能力。从图3所示的相对误差曲线和数据分析可知:(1) 整体上,除了DSS模型出现了一定的预测偏差之外,其余三个模型的预测曲线随着时间的增大都逐渐趋向于0,即表明预测效果较好;(2) 在测试的初始阶段,RE曲线的起伏表明模型正在对数据进行拟合适应,其中光滑样条回归模型的波动程度较小,表明该模型对数据的拟合适应性较强。
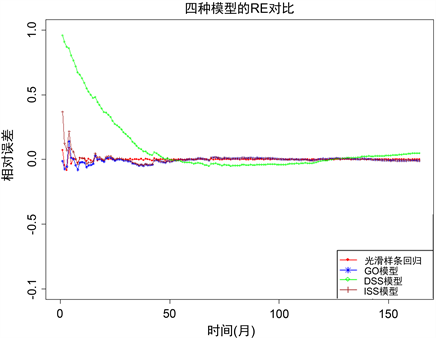
Figure 3. Comparison of relative error curves for four different models
图3. 四种模型的相对误差曲线对比
4. 结论
在软件可靠性研究中,单位时间内累计发生失效次数对软件可靠性起决定作用。本文以Tomcat服务器累计失效数为研究对象,提出一种非参数可靠性模型——光滑样条回归模型,将该模型与传统的NHPP类可靠性增长模型进行对比分析。通过绘制拟合图、预测图以及计算评估指标得出具体结论,光滑样条回归软件可靠性模型的拟合和预测效果更好,且对数据具有较强的稳健性和适应性。
基金项目
国家自然科学基金项目(No.72361008),贵州省交通运输厅科技项目(No.2022-321-013)。
NOTES
*通讯作者。