1. 引言
二十世纪三十年代P. Jordan最早给出了约当代数的概念。约当代数是在量子力学中引入的一类非结合代数,在很多领域都有广泛的应用。最近几十年,约当代数得到了广泛的研究,并应用于微分几何、量子群、李理论等数学领域 [1] [2] [3] 。现阶段,约当代数作为独立的代数结构,发展迅速。在约当代数的基础上出现了一些其它的代数,比如预约当代数 [4] 、J-dendriform代数 [5] 等。其中侯冬平做了预约当双代数和Loday代数的约当代数
类似
[6] 。Y. Sun等人给出了低维预约当代数的完全分类 [4] 。本文在此基础上,研究了二维预约当代数的Rota-Baxter算子,并构造了一些特殊的J-dendriform代数,为预约当代数的研究提供一些基础。
2. 预备知识
定义1.1 ( [6] )在线性空间J上定义一个双线性的乘法“ ”,如果满足
”,如果满足
其中
,
,则称
为预约当代数。
定义1.2 ( [6] )设
是一个预约当代数,V是一个线性空间,如果
两个线性映射满足
其中
,
,则称
为
的一个双模。
设
是一个预约当代数,用L和R分别表示J上的左乘算子和右乘算子,即
,其中
。
设
是预约当代数,V是线性空间,对于任何的线性映射
,定义映射
,其中
则称
是
的一个对偶映射。
定理1.3 ( [6] )设
是预约当代数,且
是
的双模,则
是
的双模。
定理1.4 ( [6] )设
是预约当代数,
是线性映射,则
是预约当代数
的一个双模当且仅当直和空间
上定义
时,
为预约当代数。
定义1.5 ( [5] )设
是预约当代数,
是
的一个双模,如果线性映射
满足
其中
,则称T为预约当代数
的O-算子。
定义1.6 ( [5] )设
是预约当代数,如果线性映射
满足
(2.1)
其中
,则称R为预约当代数
的Rota-Baxter算子。
定理1.7 ( [6] )设V是线性空间,
是预约当代数,
是线性映射,则
是预约
当代数
上JP-方程的对称解当且仅当T是
上与双模
相关的O-算子。
定义1.8 ( [5] )设A是一个线性空间,
是A上的两个双线性的代数运算,如果满足
其中
,
,
,
,则称
为J-dendriform代数。
定理1.9 ( [5] )
是一个预约当代数,R是
的Rota-Baxter算子,在J上定义
其中
,则
是J-dendriform代数。
3. 二维预约当代数上的算子
定理2.1 ( [4] )
是二维预约当代数,
是J的一组基,则
在同构意义下有以下几种(表1)。

Table 1. Classification of two-dimensional pre-Jordan algebra
表1. 二维预约当代数的分类
定理2.2令
设
是二维预约当代数,
是J的一组基,则J上的Rota-Baxter算子为:
1) 对于
型的预约当代数,它的Rota-Baxter算子为O;
2) 对于
型的预约当代数,它的Rota-Baxter算子为O;
3) 对于
型的预约当代数,它的Rota-Baxter算子为R1;
4) 对于
型的预约当代数,它的Rota-Baxter算子为R1;
5) 对于
型的预约当代数,它的Rota-Baxter算子为R2;
6) 对于
型的预约当代数,它的Rota-Baxter算子为R1;
7) 对于
型的预约当代数,它的Rota-Baxter算子为R1、R3、R4;
8) 对于
型的预约当代数,它的Rota-Baxter算子为R1、R3、R4;
9) 对于
型的预约当代数,它的Rota-Baxter算子为R1、R3、R4;
10) 对于
型的预约当代数,它的Rota-Baxter算子在
下的矩阵R5、R6;
11) 对于
型的预约当代数,其上的任意线性变换都是它的Rota-Baxter算子。
证明:1) 设
是二维预约当代数,R是
上的Rota-Baxter算子,设R在
下的矩阵为
,由于R满足(1.1),则
(3.1)
对于
型预约当代数,由(2.1)可得
(3.2)
解方程可得
。因此,
型预约当代数的Rota-Baxter算子为0。
2) 对于
型预约当代数,由(2.1)可得
解方程可得
。因此,
型预约当代数的Rota-Baxter算子为0。
3) 对于
型预约当代数,由(2.1)可得
解方程可得
。因此,
型预约当代数的Rota-Baxter算子为R1。
4) 对于
型预约当代数,由(2.1)可得
解方程可得
。因此,
型预约当代数的Rota-Baxter算子为R1。
5) 对于
型预约当代数,由(2.1)可得
解方程可得
。因此,
型预约当代数的Rota-Baxter算子为R2。
6) 对于
型预约当代数,由(2.1)可得
解方程可得
。因此,
型预约当代数的Rota-Baxter算子为R1。
7) 对于
型预约当代数,由(2.1)可得
分情况讨论:
① 若
,则
,此时
的Rota-Baxter算子为R1。
② 若
,则
,
i) 若
,则
,此时
的Rota-Baxter算子为R3,
ii) 若
,则
,此时
的Rota-Baxter算子为R4。因此,
型预约当代数的Rota-Baxter算子为R1、R3、R4。
8) 对于
型预约当代数,证明方法与(7)相同,得到了
型预约当代数的Rota-Baxter算子为R1、R3、R4。
9) 对于
型预约当代数,证明方法与(7)相同,得到了
型预约当代数的Rota-Baxter算子为R1、R3、R4。
10) 对于
型的预约当代数,由(2.1)可得
分情况讨论:
① 若
,则
,此时
的Rota-Baxter算子为R5。
② 若
,则
,此时
的Rota-Baxter算子为R6。
因此,
型预约当代数的Rota-Baxter算子为R5、R6。
11) 对于
型的预约当代数,
上的任意线性变换都是它的Rota-Baxter算子。
4. 特殊四维预约当代数上的JP-方程的解
定理3.1设
是二维预约当代数,则由定理1.7对应的四维预约当代数
的特征矩阵为:
1)
的特征矩阵为
2)
的特征矩阵为
3)
的特征矩阵为
4)
的特征矩阵为
5)
的特征矩阵为
6)
的特征矩阵为
7)
的特征矩阵为
8)
的特征矩阵为
9)
的特征矩阵为
10)
的特征矩阵为
11)
的特征矩阵为
证明:对于二维预约当代数
,设
是
的一组基,
是
的对偶基。根据定理1.7,在
上
则
。同理可得
。
由于
则
。同理可得
。
其余情况与(1)的证明方法类似。
定理3.2 设
是二维预约当代数,则由定理1.7构造的预约当代数
上JP-方程的解为:
1) 令
,则
是
上的JP-方程的解;
2) 令
,则
是
上的JP-方程的解;
3) 令
,则
是
上的JP-方程的解;
4) 令
,则
是
上的JP-方程的解;
5) 令
则
是
上的JP-方程的解;
6) 令
则
是
上的JP-方程的解;
7) 令
则
是
上的JP-方程的解;
8) 令
,则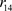 是
上的
是
上的
JP-方程的解。
证明:对于
型预约当代数,由定理2.2知R1是
的Rota-Baxter算子,因此
由定理1.7可知,
是
上的JP-方程的解。
其余情况与(1)的证明方法类似。
5. J-Dendriform代数的构造
定理4.1设
是二维预约当代数,
是J的一组基,则由定理1.9构造的J-dendriform代数为:
1)
上由R1构造的J-dendriform代数为
,
,其余全部为0;
2)
上由R1构造的J-dendriform代数为
,其余全部为0;
3)
上由R2由构造的J-dendriform代数为
,
;
4)
上由R1构造的J-dendriform代数为
,
,其余全部为0;
5)
上由R1构造的J-dendriform代数为
,其余全部为0;由R3构造的J-dendriform代数为
,
,
,其余全部为0;由R4构造的J-dendriform代数为
,
,
,
,
,
,其余全
部为0;
6)
上由R1构造的J-dendriform代数为
,其余全部为0;由R3构造的J-dendriform代数为
,
,
,其余全部为0;由R4构造的J-dendriform代数为
,
,
,
,
,
,其余全
部为0;
7)
上由R1构造的J-dendriform代数为
,
,其余全部为0;由R3构造的J-dendriform代数为
,
,
,
,其余全部为0;由R4
构造的J-dendriform代数为
,
,
,
,
,
,
,
;
8)
上由R5构造的J-dendriform代数为
,
,由R6构造的J-dendriform代数为
,
,其余全部为0。
证明:根据定理1.9,对于
型二维预约当代数,它的Rota-Baxter算子为R1,则
,
。故
其余情况与(1)的证明方法类似。
6. 结论
本文主要研究了二维预约当代数的Rota-Baxter算子的全部分类,并得到了特殊的四维预约当代数上JP-方程的解,并构造了一些特殊的J-dendriform代数。此外,还可以继续研究三维预约当代数上的Rota-Baxter算子,或者考虑其它形式的低维预约当代数上的JP-方程的解,这些问题都可以继续深入研究。