基于污水流行病原理的病毒检测点选址问题研究——以湖南省娄底市为例

Research on the Location of Virus Detection Points Based on the Principle of Sewage Epidemic—Taking Loudi City, Hunan Province as an Example

摘要: 近年来，我国的公共卫生事件具有明显的突发性、不确定性等特点，对于突发性的病毒，当病毒大规模爆发时，污水流行病学(WEB)作为临床监测的补充方法，相比血常规、特异性血清检查和核酸检测等常规检测方法有着更简便、广泛和接近实时监测的优点，对于区域疾病监测有着广泛的应用前景。该项技术取决于污水收集系统等基础设施的发展与完善，然而我国在该方面的研究、应用起步较晚，目前我国有关污水病毒检测的研究取样范围大多局限于一两座污水处理厂，同时也没有标准化的WBE应用方案。基于此，本文以湖南省娄底市为例，考虑各社区人口分布以及建设成本，结合WBE的三阶段处理效率，即对象释放效率、管道输送效率、检测回收效率，先后通过K-means聚类模型和TOPSIS综合评价法，研究娄底市区常规污水疾病采样点的优化选址问题。

Abstract: In recent years, China’s public health events have obvious suddenness, uncertainty and other characteristics, for sudden viruses, when the virus large-scale outbreak, wastewater based epide-miology (WEB) as a supplementary method of clinical surveillance, compared with routine detec-tion methods such as blood routine, specific serum test and nucleic acid detection has the ad-vantages of simpler, extensive and near-real-time monitoring, for regional disease surveillance has a wide application prospects. The technology depends on the development and improvement of infrastructure such as sewage collection systems, but China’s research and application in this area started late, and most of the research and sampling scope of sewage virus detection in China is limited to one or two sewage treatment plants, and there is no standardized WBE application program. Based on this, this paper takes Loudi City as the object, combined with the three-stage treatment efficiency of WBE, namely object release efficiency, pipeline transportation efficiency, and detection and recovery efficiency, and successively uses K-means clustering model and TOPSIS comprehensive evaluation method to study the optimal site selection of conventional sewage dis-ease sampling points in Loudi urban area.

1. 引言

近年来我国不断发生突发性的公共卫生事件，这些事件具有不确定性和迅速传播的特点，给公共卫生安全带来了巨大挑战。传统的疾病监测方法存在一定的局限性，比如需要大规模的样本采集和检测，耗时耗力且效率较低。因此，寻找一种更简便、广泛且接近实时的监测方法，对于及时追踪和判断公共卫生事件的发生与传播至关重要。

污水流行病学作为一种新兴的监测方法，基于人们感染疾病后代谢物在污水中的排放，通过分析市政污水处理厂进水中的污染物或生物标记物浓度，结合相关参数进行化学分析，可以探究与疾病、药物滥用、健康等有关的公众信息，并估计感染人数 [1] 。与传统的污水处理厂相比，污水监测系统可以更好地了解病毒在社会中的传播情况，通过监测城市居住区的污水中病毒残留物质，可以追踪病毒在社会中的传播程度。

然而，目前我国污水流行病学研究和应用起步较晚，研究范围较窄且缺乏标准化的应用方案。因此，为了更好地应对公共卫生事件，有必要进行相关研究，特别是在疫情传播路径和病毒监测目的方面 [2] 。科学合理的污水疾病检测点选址对于区域疾病的监测具有重要意义，能够提供有效的数据支持和参考，帮助当地公共卫生部门更好地了解病毒传播情况，并采取相应的措施进行预防和控制。因此，研究污水流行病学在公共卫生事件监测中的应用是非常重要的，它能够为公众的健康和社会的稳定提供有力保障。

2. 疾病监测点选址模型设计思路

2.1. 选址影响因素

为了使本文的研究更具有一般性，在污水疾病检测点的选址过程中，本文充分考虑客观影响因素，包括居民的地理位置、居民的人口数量以及现有污水系统布局等 [3] 。在人口密集区和流动人口较多的地区选择监测点，考虑污水负荷和处理能力，确保监测点覆盖的范围不会过大或过小，提高检测的准确性和效率。同时充分考虑监测点的建设成本，使污水疾病检测点能有效地覆盖范围内的居民点的同时尽量减少污水疾病采样点的建设及运营所需要的总费用，以及考虑污水回收的效率 [4] 。其中，人口密度、管道输送成本、系统建设成本以及污水回收效率是本文选址设计过程中的重点。

2.2. 数据来源

本文采集的数据包含娄底市各乡镇人口数量、各乡镇经纬度坐标以及现有污水系统布局等作为污水常规化监测点选址的资料来源。其中人口数据来源于娄底市统计局娄底第七次人口普查乡镇数据，包含按区域划分的96个乡镇人口数量，经纬度数据根据卫星地图查询各乡镇对应经纬度坐标、现有六所主要的污水处理系统布局信息来源于娄底市生态环境局。

2.3. 模型构建思路

本研究的目标是在96个居民点组成的区域中，选出一定数量的污水疾病监测点，并建立居民点到监测点之间的管道运输网络。为了达到最小化成本、最大化覆盖范围和最大化回收效率的目标，本文采用了以下方法和评估指标。

首先，根据每个居民点到其他居民点的距离计算，建立了距离矩阵。然后，采用K-means聚类算法，将距离矩阵作为输入数据，确定了10个聚类中心点，这些聚类中心点被视为潜在的监测点备选。

接下来，对每个备选的监测点，计算它们与区域内所有居民点之间的距离，作为监测点到居民点之间的管道运输成本。此外，人为设定每个备选点的固定建设成本，并计算备选点所覆盖的人口密度。还利用现有污水厂地理位置数据，计算每个备选点到最近的污水厂之间的距离，并根据检测点的人口数量计算各个备选点的回收效率。

经过以上计算，我们可以使用TOPSIS综合评价法对每个备选的监测点进行评估。首先，确定评估对象，将每个备选的监测点作为评估对象。其次，归一化三个权重指标，使其在0到1的范围内。然后，构建决策矩阵，将每个备选监测点的评价指标按照权重加权后构建成一个决策矩阵。接下来，确定理想解和负理想解。理想解是在各个指标上取最大值的情况，而负理想解则相反，取在各个指标上的最小值。然后，计算每个备选点与理想解之间的距离，使用欧氏距离度量。这个距离表示备选点与理想解之间的差异程度。同时，计算每个备选点与负理想解之间的距离，表示备选点相对于负理想解的差异程度。最后，根据与理想解和负理想解的距离，计算每个备选点的综合评价值。综合评价值反映了备选点相对于理想解和负理想解的优劣程度，数值越大表示备选点越优秀。通过选择综合评价值最高的备选点，我们可以确定最适合的污水疾病监测点。该评估方法综合考虑了多个指标的权重和比较，能够帮助决策者进行科学合理的决策。

通过上述步骤，可以得到最优的污水疾病监测点的选址方案，该方案在最小化成本、最大化覆盖范围和回收效率方面取得了较好的平衡。这个方法不仅充分考虑到了居民点的地理位置、人口数量和现有污水系统布局等客观因素，还利用了K-means聚类算法和TOPSIS综合评价法来实现选址决策的科学性和合理性。同时，该方法综合考虑了各种影响因素，旨在为污水流行病学的应用提供更具指导性和实用性的解决方案。

3. 模污水疾病监测点选址数学模型

3.1. 模型假设

① 不考虑疾病检测系统出故障的情况，即设备工作状态一直良好；② 每个污水处理点的处理能力一样，选址点之间是相互独立的，即一个选址点不会受到其他选址点的影响；③ 该城市的地势平坦，污水排放到污水处理点的速度均匀，不受其他因素影响；④ 不考虑土地成本差异，认为各个污水监测点的选址点土地成本一样；⑤ 假设每个潜在的监测点的建设成本是固定的，不考虑其他因素对建设成本的影响。

3.2. 模型的建立与求解

3.2.1. 基于K-Means聚类对居民点进行分类

本文的目标是从96个居民点组成的区域中，选出一定数量的疾病监测点，建立社区居民点到常规疾病监测点的管道运输网络，实现社区与最近的监测点之间平均距离最小。首先考虑的是居民点的平均最短距离，解决的是多源选址问题，找到常规疾病监测点的最佳选址 [5] 。

通过数据分析，对现有居民点地地理位置进行类型划分。聚类分析是对个体或对象按照差异性原则进行分类，形成同类个体或对象之间的差异最小化，不同个体或对象之间的差异最大化，针对居民点疾病采样点的建设问题选择K-means算法可以简洁有效地对数据进行聚类划分 [6] 。

其思路是(如下图1)：先从给定的数据集中，随机选择K个初始的聚类中心，然后统计每个样本点的间距，再根据距离最近原则，把样本点分配到对应的簇中；在下一次迭代的过程中，重新统计各簇的聚类中心，直到达到终止条件或达到最大循环次数为止。最终得到每个聚类组的点集和聚类中心的坐标。聚类结果应让同一簇内的样本点距离尽量的近，而不同簇的样本点间的距离相距尽量的远。

Figure 1. Cluster flowchart

图1. 聚类流程图

样本点之间的欧式距离公式表示为：

$d\left(x_i,x_j\right)=\sqrt{{\displaystyle \underset{i=j,i,j=1}{\overset{n}{\sum }}{\left(x_i-x_j\right)}^2}}$ (1)

其中， $d\left(x_i,x_j\right)$ 表示样本点 $x_i$ 和 $x_j$ 之间的欧氏距离， $x_i=\left(x_{i1},x_i{}_2,\cdots ,x_{ip}\right)$ 和 $x_j=\left(x_{j1},x_j{}_2,\cdots ,x_{jp}\right)$ 为维度等于p的任意两个样本点， $x_{ip}$ 表示样本点i对应p个维度的具体取值。

数据集D的平均样本距离表示为：

$\text{Mean}\text{Dist}\left(D\right)=\frac{1}{C_n^2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{i}{\sum }}d\left(x_i,x_j\right)}}$ (2)

其中， $C_n^2$ 是n个样本点中随机选取两个样本点的所有可选的组合数。

数据集D的误差平方和表示为：

$\text{SSE}={\displaystyle \underset{i=1}{\overset{k}{\sum }}{\displaystyle \underset{x\in c_i}{\sum }d{\left(x,c_i\right)}^2}}$ (3)

其中，k是簇的个数， $c_i$ 是第i个簇的聚类中心， $d\left(x,c_i\right)$ 指的是数据点x与 $c_i$ 的相异度。不同的相异度计算常常会导致不同的聚类结果。SSE的大小即可说明样本点的密集程度。

通过计算每个居民点之间的距离并使用K-means聚类算法，得到一组备选检测点，得到的聚类结果如下图2、表1：

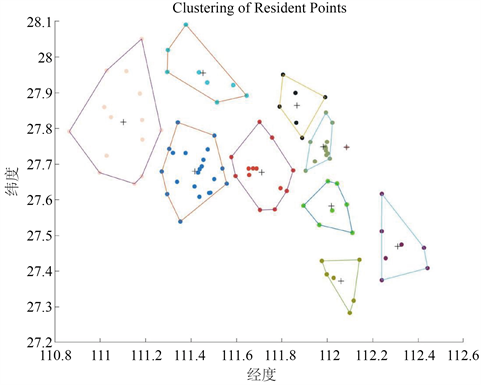
Figure 2. 10 potential sampling points after clustering

图2. 聚类后的10个潜在采样点

Table 1. Potential point location and corresponding number of people covered

表1. 潜在点位置及对应的覆盖人数

3.2.2. 计算潜在检测点的对应指标

在得到十个潜在检测备选点之后，本文结合现有的污水处理厂地理位置，认为各检测点的运输成本、人口覆盖数量、污水回收效率是主要影响因素。下面对这三个指标进行计算：

a) 各备选检测点运输成本

计算每个备选检测点到居民点的距离作为管道运输成本，人为设定每个检测点的建设成本，将管道运输成本与建设成本之和作为总成本，假设成本越大备选检测点被选择的可能性越小。

b) 各潜在检测点人口覆盖数量

计算每个聚类中心点所覆盖的人口数量，作为人口数量指标，假设人口覆盖数量越大备选检测点被选择的可能性越大。

c) 各潜在检测点的污水回收效率

为得到各备选疾病检测点的污水回收效率，利用现有的污水处理厂地理位置信息，考虑检测点到污水处理厂的距离、各检测点所覆盖的人口数量、以及各污水处理厂的处理能力。假设距离越远，运输的成本和损耗越大，因此对效率有负面影响；假设人口数量与产生的污水量成正比；假设处理能力越大，效率越高。

使用欧氏距离计算每个疾病监测点到最近的污水厂的距离，各潜在检测点与现有的污水厂地理位置关系如下图3。

定义回收效率函数为：

$E_i=\frac{P_i\times C_j}{D_{ij}\times \max P}$ (4)

其中， $E_i$ 是检测点i的回收效率， $P_i$ 是检测点i的人口数量， $C_j$ 是处理厂j的处理能力， $D_{ij}$ 是检测点i到处理厂j的距离， $\max P$ 是所有检测点覆盖的人口数量最大值，用于归一化人口数量，最后，为每个检测点选择回收效率最高(即 $E_i$ 最大)的处理厂，并计算其回收效率 $E_i$ ，假设回收效率越高检测点被选择的可能性越大。

最终得到的三个指标如下表2。

为确保不同权重之间具有相同的尺度范围，减少尺度差异对模型的影响，以便它们能够在模型中平等地进行比较和综合考虑，本文对以上三个指标进行归一化处理，消除权重之间的量纲差异，使它们具有可比性。

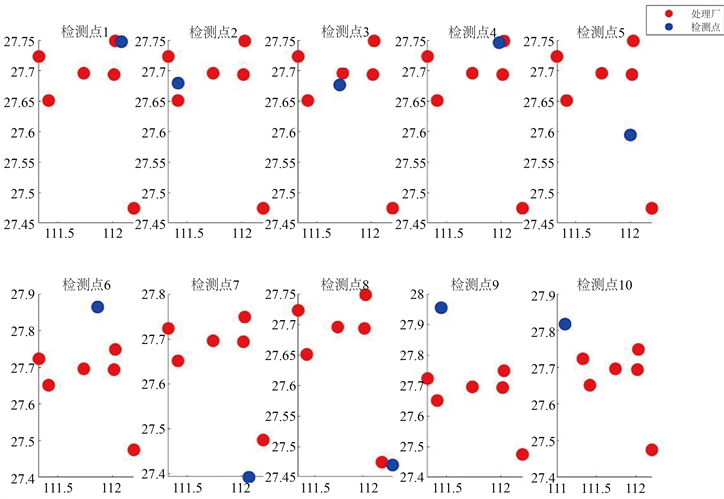
Figure 3. Geographical location relationship between each alternative site and existing sewage treatment plants

图3. 各备选点与现有的污水厂地理位置关系

Table 2. Evaluation indicators for each potential detection point

表2. 各潜在检测点评估指标

3.2.3. 基于多属性决策分析对十个潜在检测点进行选择

TOPSIS法是根据评价对象与理想化目标的接近程度进行排序的方法。基于归一化后的原始数据矩阵，找出有限方案中的最优方案和最劣方案，进而得出某一方案与最优的方案和最劣方案之间的差值，从而得出与理想方案的接近程度 [7] 。其基本步骤如下：

标准化数据：为确保不同权重之间具有相同的尺度范围，减少尺度差异对模型的影响，以便它们能够在模型中平等地进行比较和综合考虑，本文将每个备选方案的属性值标准化到0到1之间，以便在不同属性之间进行比较。得到标准化的指标如下图4所示：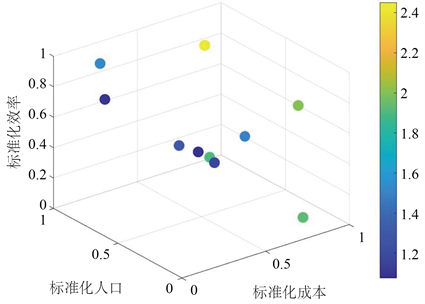

Figure 4. Scatter plot of three indicators

图4. 三个指标散点图

Figure 5. Site selection evaluation results

图5. 选址点评估结果

计算与正理想解和负理想解的距离：对每个备选方案，计算其与正理想解和负理想解之间的距离，通常使用欧氏距离或其他距离度量方法。

综合评分：计算每个备选方案的综合评分，这可以通过计算距离与负理想解的距离之比来实现。距离越小，综合评分越高，反之亦然。

排序或选择：按照综合评分对备选方案进行排序或选择。得分最高的方案排名最高，表示最优选择。得到最终结果如上图5所示。

综上，在娄底市的污水检测点选址中，聚类中心点10的评分排第一即点(111.102143，27.818015)，是娄底市建立污水疾病检测点的最佳选址位置，其次是聚类中心点2、8、7、3、9，评分分别为1.97、1.70、1.64、1.51、1.50，均比较适合用于疾病监测点的选址，聚类中心点1、5、6、4的评分较低，不太适合作为污水检测点。

4. 结语

在娄底市污水疾病检测点选址中，通过K-means聚类模型和TOPSIS综合评价法，得出了优化选址的具体结果。其中，聚类中心点10的评分最高，评分为111.102143，坐标为(111.102143，27.818015)，被认为是最佳选址位置。其次是聚类中心点2、8、7、3、9，它们的评分分别为1.97、1.70、1.64、1.51和1.50，也适合作为污水检测点。而聚类中心点1、5、6、4的评分分别为1.01、0.69、0.54、0.00，分数较低，不太适合作为污水检测点。

这项研究有助于解决污水病毒检测点选址的问题。随着公共卫生事件(如突发性疫情)的发生，通过污水流行病学方法来进行临床监测已被证明具有很多优点，例如简便、广泛和接近实时监测等等。而在这个方法中，污水检测点的选址对于区域疾病监测至关重要。本文研究的结果提供了娄底市区常规污水疾病检测点的优化选址建议，根据评分高低确定了最佳选址位置和其他适合的选址点。这将为娄底市建立污水疾病检测点提供指导和参考，有助于提高疫情监测的精确性和有效性。

此外，该研究方法可以为其他地区的污水检测点选址提供有价值的见解。通过结合人口分布、建设成本和污水处理系统等因素，综合评价不同候选点的处理效率，可以帮助决策者更加科学地选择合适的污水检测点位置。这对于公共卫生事件的监测和防控具有重要意义，有助于及早发现和应对潜在的疫情风险。

5. 展望

本文所描述的方法和评估指标是为了在选址污水疾病监测点时最小化成本、最大化覆盖范围和回收效率。这一方法注重利益平衡和资源优化，有助于科学合理地进行决策。然而，需要指出的是，本文的研究方案可能存在一些可行性和局限性。首先，该研究的可行性会受到特定地区和情境的影响。不同地区的地理条件、人口分布和污水系统的布局等因素会影响到选址的可行性和有效性。因此，在将这种方法应用于实际项目之前，需要对具体地区进行充分的调研和分析。

其次，本文可能未考虑到一些特定的政治、环境和社会因素。例如，政府的政策导向、环保规定和社会支持程度等因素可能会影响到监测点选址和管道运输网络的建设。因此，如果在具体的政治背景下，这些因素对选址决策有显著影响，那么在决策过程中需要考虑这些因素。

最后，本文所使用的方法可能还存在一些技术上的限制。例如，K-means聚类算法在确定聚类中心点时可能存在一定的主观性，而且该方法不能保证找到全局最优解。此外，TOPSIS综合评价法在权重的确定和距离度量上也存在一定的主观性。

综上所述，本文提供了一种科学合理的选址方案，以平衡成本、覆盖范围和回收效率。但是需要注意的是，具体应用该方案时需要进行实地调研，并充分考虑特定地区和情境的因素，以及与当地政策、环境和社会因素的协调。

基金项目

本研究由湖南省大学生创新创业训练计划项目“疫情常态化背景下核酸检测点优化布局研究——以娄底市为例”和湖南人文科技学院数学应用与实践创新创业教育中心、科学计算与数据分析创新创业教育中心资助。

NOTES

^*通讯作者。