1. 引言
数字高程模型(Digital Elevation Model, DEM)作为地表高程的数字化表达,被广泛应用于地貌、水文、测绘、灾害监测和控制等领域 [1] ,是战时快速获取境外信息,实现由海对陆打击的重要保障。在现有的全球公开数字高程数据中,美国航天飞机雷达测绘任务(Shuttle Radar Topography Mission, SRTM)在覆盖范围、高程精度、公开程度等各方面综合评价最高,已成为应用最为广泛的全球DEM数据 [2] 。但是,SRTM受观测手段、地形条件、植被覆盖等因素的影响,虽经过多次修正,但其高程仍然存在不可忽略的误差,且在不同区域高程精度往往差异较大。
针对SRTM所存在的高程误差,国内外学者尝试利用各类精度更高的参考数据对SRTM高程误差进行修正,如高精度GNSS测量点 [3] [4] 、机载激光雷达高程数据 [5] [6] ,高精度DEM数据 [7] 等。但是,上述参考数据往往分布区域受限、获取和制作难度大,难以依据实际需要对大范围、任意区域的SRTM进行高程误差修正。2003年美国国家航空航天局发射的冰、云和陆地高程卫星(The Ice, Cloud and Elevation Satellite, ICESat)携带了激光测高载荷GLAS (Geoscience Laser Altimeter System),因其近全球覆盖,测高精度高等优势,ICESat/GLAS数据被逐步应用于SRTM高程修正中。杜小平等 [8] 在中国典型高海拔山区和低海拔沿海平原地区建立了ICESat/GLAS和SRTM之间一元线性回归模型,提高了特定区域的SRTM高程精度;Su等 [9] 以ICESat/ATLAS为参考高程数据,通过建立基于树高、冠层覆盖度和坡度的SRTM高程误差多元线性回归模型,修正了内华达山脉植被覆盖山区的SRTM;秦臣臣等 [10] 借助ICESat/GLAS数据,采用插值方法对误差数据构建误差曲面,以误差曲面修正SRTM;杨帅等 [11] 基于ICESat/GLAS数据,采用多种机器学习的方法对配准后的SRTM进行修正。以上基于ICESat/GLAS数据对SRTM的高程误差的修正工作为提供高程更为精准的全球SRTM奠定了基础,但ICESat在2009年失效,其数据也相应停止更新,无法实现更具现势性的SRTM修正。2018年9月,第二代冰、云和陆地高程卫星(The Ice, Cloud and Elevation Satellite-2, ICESat-2)成功发射,作为光子体制的星载激光测高卫星,相较于线性体制的ICESat,其搭载的先进地形激光高度计系统(Advanced Topographic Laser Altimeter System, ATLAS),具有低能量、高灵敏度、高重复频率的优势,可以获取光斑更小、密度更高的高程数据 [12] ,同时其数据高程精度也优于ICESat/GLAS。因此,应用ICESat-2/ATLAS数据有利于实现更加精准、更具现势性的SRTM高程误差修正结果。
随着ICESat-2/ATLAS数据的公开发放,Magruder等 [13] 针对ICESat-2/ATLAS数据特点从中提取分类为地表的光子作为高程参考点,结合Landsat8影像,采用多项式回归方程建立SRTM修正模型,修正过后的SRTM相比原始SRTM高程误差得到明显改善。但是,由于SRTM高程误差与其影响因素之间往往是复杂的非线性关系,简单数学表达的多项式回归方程难以充分表达这种关系,应用此种方法修正的SRTM高程精度仍不够稳定,存在一定的局限性。
为此,本文提出一种基于粒子群算法优化的随机森林(PSO-RF) SRTM高程误差修正方法。首先,以ICESat-2/ATLAS ATL03数据为基础提取参考高程光子;然后,构建以经纬度、坡度、坡向、地形起伏度和地表覆盖类型为响应变量的修正模型;最后,采用PSO-RF建立SRTM高程误差修正模型,利用数据训练后的模型结合SRTM每个像元对应的响应变量信息,实现对SRTM的高程误差修正,进一步提高SRTM的高程精度。
2. 研究区域与数据来源
2.1. 研究区域概况
本文选择的研究区域位于美国西海岸内华达山脉和圣华金河谷地区(36.3˚~38.3˚N, 117.5˚~120.7˚W)。如图1所示,该区域东侧为高山地,西侧为平原,地形和地表覆盖类型呈现多样性,能够较为全面地检验本文方法的有效性。
2.2. 数据来源
2.2.1. SRTM数据
SRTM是由美国国家航空航天局、美国国家图像与测绘局和德国宇航中心共同合作,采用合成孔径干涉雷达测量技术生成的全球DEM数据,其覆盖了全球约80%的陆地面积(56˚S~60˚N)。自发布以来,SRTM历经多次修订,本文使用数据版本为GL1,其分辨率为1'' (约30 m),以WGS-84坐标系为其地理坐标系,以EGM96大地水准面为其高程基准。该版本的SRTM数据融合了ASTER GDEM V2、USGS GMTED等多源、多类型DEM数据,解决了之前版本SRTM所存在的部分区域的空洞问题,标称绝对高程精度优于16 m (LE90) [2] 。
2.2.2. 全球地表覆盖数据
本文选择我国自主研发的GlobeLand30 (V2020)作为实验所用全球地表覆盖数据,该数据由中国科学院空天信息创新研究院利用美国陆地资源卫星(Landsat)、中国环境减灾卫星(HJ-1)、高分一号卫星(GF-1)等多源影像制作而成,空间分辨率为30米,包括耕地、林地、草地、人造地表等10个地表类型。经抽样验证,GlobeLand30 (V2020)的总体精度优于85%,能够为本文方法提供准确的地表覆盖数据支撑。
2.2.3. ICESat-2/ATLAS数据
ICESat-2搭载的ATLAS采用微脉冲多波束光子计数激光雷达技术,以10 kHz的重复频率发射激光波束,通过衍射光学元件将其分成三对激光子束,每对子束均包含强、弱光束 [14] ,三对子束在沿轨方向平行排列,在垂轨方向上间距约3 km,任一子束中强弱光束垂轨方向间相距约90 m,沿轨方向间距约2.5 km,二者能量比为4:1,每个波束均可表征为直径约17 m,沿轨间距0.7 m的地表光斑 [15] 。由于强光束相对弱光束具有更优的地形的反演精度 [16] [17] ,为提升本文所提PSO-RF方法的效率与鲁棒性,减少冗余数据,本文只选取强光束数据用于提取参考高程光子,其数据分布可如图2所示。

Figure 2. Distribution of ICESat-2/ATLAS data in the study area
图2. 研究区域ICESat-2/ATLAS数据分布情况
ICESat-2/ATLAS共分为Level0-Level3四级数据,其下又细分为ATL00-ATL21 (无ATL05) 21种产品。其中,与本文相关的为Level2级数据产品ATL03和Level3A级数据产品ATL08。ATL03为全球定位光子数据,记录了光子精确的经纬度信息,以及相对于参考椭球的大地高信息。ATL08为陆地和植被高程数据,该数据以ATL03数据为基础,通过差分渐进高斯自适应去噪算法(Differential, Regressive, and Gaussian Adaptive Nearest Neighbor, DRAGANN)得到信号光子,并采用迭代滤波的方式将信号光子分类为冠顶、冠层和地表光子,进而重采样为100 m空间分辨率的冠顶和地表高程产品。
2.2.4. LIDAR DTM数据
为验证修正SRTM的高程精度,以美国国家生态观测站网络(National Ecological Observatory Network, NEON)发布的高精度的LIDAR DTM作为验证数据,其分辨率为1 m,标称垂直和水平精度分别为0.36 m和0.40 m,其分布情况可如图3所示。该数据以WGS-84为其空间参考坐标系,NAVD88为其高程基准,为对后续进行结果精度验证,本文采用美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA)开发的VDatum软件将其转换至EGM96高程基准。

Figure 3. Distribution of LIDAR DTM
图3. LIDAR DTM分布图
3. 研究方法
3.1. 参考高程光子提取
依据DRAGANN去噪算法及光子分类结果,ICESat-2科学团队在ATL08中提供了光子分类标签(classed_pc_flag),标签为0、1、2、3时分别代表噪声、地表、冠层和冠顶光子。现有研究表明,DRAGANN去噪算法在中低信噪比条件下表现较好,而在强噪声环境下该方法可能导致部分信号光子被错分为噪声光子 [18] ,带来错误的光子分类结果,进而影响后续高程修正过程。因此,本文方法首先通过ATL03数据中的信号光子置信度标签(signal_conf_ph),粗略计算ATL03数据的信噪比。对处于中低信噪比条件下的ATL03数据,利用ATL03和ATL08之间的关联关系将光子的分类信息关联到ATL03中,直接提取地表光子 [16] 。而对于强噪声背景下的ATL03数据,则以剪枝四叉树去噪方法为基础得到信号光子 [19] ,并结合自适应布料模拟方法精准提取地表光子 [20] 。最后,综合不同噪声背景下的地表光子,将其作为参考高程光子参与后续误差修正。需要指出是,由于ATL03数据中的光子高程是以WGS-84参考椭球为基准的椭球高度,因此,为统一高程基准,同LiDAR DTM相似,将光子相对椭球的大地高也转换到EGM96高程基准。
对SRTM数据进行裁剪、镶嵌得到研究区域的高程数据,然后进行地理处理得到坡度、坡向、地形起伏度数据,利用双线性内插提取得到光子所在位置处的地形因子信息。
3.2. 地形因子与地表覆盖类型参数提取
对SRTM数据进行裁剪、镶嵌得到研究区域的高程数据,然后进行地理处理得到坡度、坡向、地形起伏度数据,利用双线性内插提取得到光子所在位置处的地形因子信息。
对于地表覆盖类型参数,由于Globeland30为分带UTM投影,而本文研究区域横跨第10和第11两个投影带,因此将提取的参考高程光子地理坐标系根据其所处区域分别投影至UTM Zone 10N和UTM Zone 11N坐标系,然后根据光子相应位置提取得到所属的地表覆盖类型参数。
3.3. 基于PSO-RF的SRTM高程误差修正模型构建
随机森林是Breiman提出的一种可用于解决非线性回归问题的机器学习算法,具有精度高抗噪声能力强,不易发生过拟合的优势 [21] [22] 。因此,本文构造RF回归模型对SRTM进行高程误差预测,同时针对其中影响模型精度的超参数,进一步融合PSO算法对超参数进行搜索寻优,以PSO-RF构造SRTM高程误差修正模型。
3.3.1. 基于RF回归的SRTM高程误差模型
本文基于RF回归算法,以经度、纬度、坡度、坡向、地形起伏度和地表覆盖类型六个响应变量构造SRTM高程误差模型:
(1)
式中,Herror为SRTM高程误差,Lat和Lon分别为纬度和经度,Sl、As、Re、Gl分别为坡度、坡向、地形起伏度和地表覆盖类型参数。
基于高程误差模型,将参考高程光子的经纬度信息[Lat, Lon]、地形因子[Sl, As, Re]和地表覆盖类型参数Gl作为模型的输入数据,光子对应的SRTM高程差值Herror作为模型目标数据,二者共同构成模型训练集。基于Bagging框架 [23] [24] ,以并行的方式组合多棵决策树,应用自助采样法(Bootstrap Sampling)对训练集进行有放回随机采样得到训练决策树的若干子训练集。随机从响应变量[Lat, Lon, Sl, As, Re, Gl]中选择n (n < 6)个变量作为决策树节点划分的候选变量,对于每个节点,依次遍历选择的n个变量对其进行划分,当划分所产生的两个数据集D1、D2中各自Herror均方差最小,且两个数据集均方差之和最小时,所对应划分的变量值j和变量值s将作为最优划分变量和划分点,其代价函数的表达式为:
(2)
式中,m1、m2为划分后的数据集D1、D2中Herror的均值,xi为变量属性。通过若干子训练集对决策树的划分,建立不同的决策树,完成随机森林高程误差模型的训练。然后,将训练的误差方程用于新的响应变量[Lat, Lon, Sl, As, Re, Gl]对应的Herror结果预测中,将各决策树结果通过取均值等方式作为模型最终结果,得到相应的高程误差。
由以上随机森林训练流程可知,决策树的个数(n_estimators)和节点划分可选择特征变量数量最大值(max_features)这两个超参数对模型的建立影响较大。因此,对于这两个超参数值,本文将通过PSO寻优进行确定。
3.3.2. 基于PSO的超参数优化
为避免由于参数设定不当而影响RF算法精度,本文利用PSO优化算法寻找RF算法中决策树个数和节点划分可选择特征变量数量最大值两个超参数的最优组合。首先依据两个超参数的解空间范围,以整数编码的方式对种群进行初始化,然后按式(3)所示经过粒子在解空间中速度和位置的迭代更新,通过比较不同参数组合下适应度函数值搜索最优参数组合。
(3)
式中,
为第k次迭代中第i个粒子的速度,
为第k次迭代中第i个粒子在超参数解空间中的位置,w为惯性权重,c1和c2为学习因子,r1和r2为
的随机数,pbest,i为第i个粒子所经历的最佳适应度函数值对应的位置,gbest为整个粒子群经历的最佳适应度函数值对应的位置。
考虑到PSO优化过程的计算效率,同时兼顾可搜索性,通过先期实验,本文将粒子群个数设置为20,最大迭代次数设置为50。同时在进行粒子速度计算时将式(4)中的惯性权重w进行线性递减以保证算法具有较好的收敛效果,递减策略为 [25] :
(4)
式中,ws为初始惯性权重,we为终止惯性权重,k为当前迭代的次数,kmax为最大迭代次数。不失一般性地,本文中kmax设为50,ws设为0.95,we设为0.4。
本文的适应度函数值采用对RF高程误差模型进行五折交叉验证的方式进行确定,将原始训练集随机分为5组,其中4组用于随机森林模型的训练,1组用于模型精度验证,验证评价指标采用均方差回归损失:
(5)
式中,N为用于验证的数据个数,Herror为预测SRTM存在的高程误差,
为真实高程误差。依次将各组用于精度验证,最终将5次精度验证结果的均值作为适应度函数值,适应度函数值越小表示此参数下模型精度越高。
3.3.3. 基于PSO-RF的SRTM高程误差修正模型
综合上述误差修正与参数优化模型,进一步建立基于PSO-RF的SRTM高程误差修正模型:
(6)
式中,Hcorrect为SRTM修正后的高程,Horiginal为原始SRTM高程。
通过PSO算法的参数寻优,利用训练集训练得到最优参数组合的RF高程误差模型,根据每个SRTM像元的响应变量[Lat, Lon, Sl, As, Re, Gl],用于SRTM高程误差结果Herror的预测中,再由求得的高程误差,结合原始SRTM高程Horiginal得到修正后的SRTM高程Hcorrect。
4. 实验结果与分析
为验证本文提出的PSO-RF修正方法在SRTM高程误差修正中的有效性、优越性,本文以LIDAR DTM数据范围为主要验证区域,将基于PSO-RF的高程误差修正模型修正的SRTM同原始SRTM、基于PR的高程误差修正模型修正的SRTM分别进行定性、定量高程精度对比
4.1. 定性分析
首先进行定性分析,以图4中黑色直线所在的位置截取高程剖面,得到原始SRTM、两种模型修正的SRTM高程剖面曲线对比图。为便于比对分析,同时也将精度更高、用于作为参考标准的LIDAR DTM所对应的剖面曲线一并进行显示。从图中红框细节部分可以看出,由于地表植被等因素产生的高程误差使得原始SRTM的剖面曲线大部分要高于LIDAR DTM剖面曲线,而经过两种模型修正后的SRTM则较好地减小了误差,其剖面曲线与LIDAR DTM剖面曲线更为接近。同时,由于实验区域高程值较大,基于PR的修正模型和基于PSO-RF的修正模型对应的剖面曲线较为接近,仅通过定性角度还难以判断两种模型的优劣,仍需进一步通过定量计算进行对比。
4.2. 定量分析
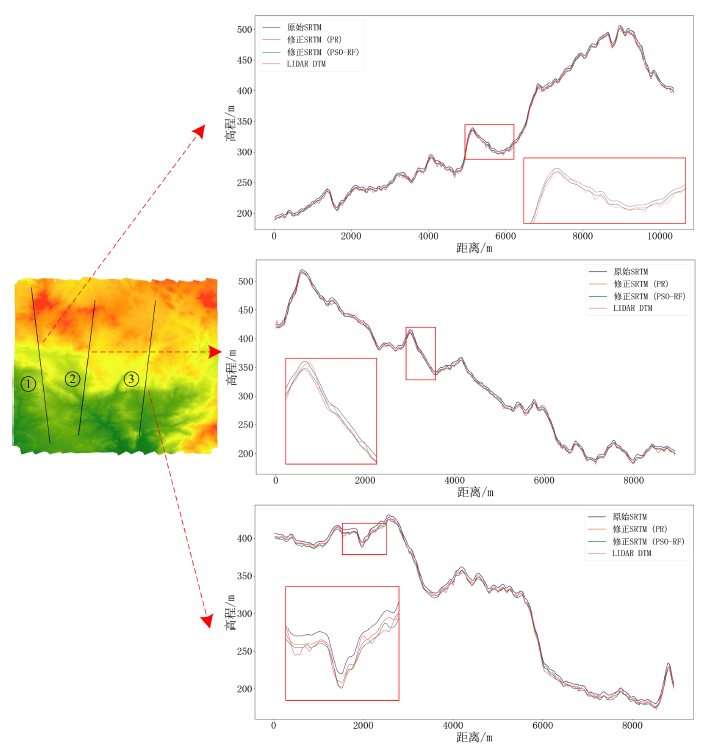
Figure 4. Comparison diagram of elevation profile curves
图4. 高程剖面曲线对比图
从图4中所示的剖面曲线中按一定间隔提取用于精度定量评价的高程点,得到相对应的原始SRTM、两种模型修正的SRTM和LIDAR DTM的高程值,以LIDAR DTM高程值作为参考高程值,计算各SRTM与参考高程之间的RMSE,计算结果如图5散点密度图所示。其中,图5(a)~(c)分别为图4中直线①处的原始SRTM、基于PR的模型修正的SRTM、基于PSO-RF的模型修正的SRTM高程精度评价结果,图5(d)~(f)分别为直线②处对应的三种SRTM高程精度评价结果,图5(g)~(i)分别为直线③处对应的三种SRTM高程精度评价结果。从图中可以看出,相对于原始SRTM,三组试验中经过模型修正后的SRTM所对应的RMSE明显减小,其中基于PR的模型对应的RMSE在三组实验中分别减小了34.4%、36.6%和38.8%,基于PSO-RF的模型对应的RMSE在三组实验中分别减小了42.7%、45.1%和46.7%,三组实验的基于PSO-RF的模型修正效果都要优于基于PR的模型,相比于基于PR的模型其可将高程误差又分别减小8.3%,8.5%和7.9%。
综合以上实验结果,在LIDAR DTM区域内,修正SRTM较好地减小了高程误差,且基于PSO-RF的修正模型精度要优于基于PR的修正模型。
5. 结论
本文以ICESat-2/ATLAS参考高程光子为基础,综合经纬度、地形因子和地表覆盖类型等多类别高程误差影响变量,利用PSO-RF构建SRTM高程误差修正模型对研究区域SRTM进行修正。经过理论分析及实验对比分析,得结论如下:
SRTM应用PSO-RF方法构造的高程误差修正模型后,高程误差得到明显的降低,修正精度好于PR方法,表明了机器学习能更好地挖掘SRTM高程误差与其影响变量存在的非线性关系,相较于现有方法,本文所提方法在解决SRTM高程误差修正问题方面具有一定的优势。
但是,本文修正后的SRTM依然在某些区域存在一定的高程误差,这可能是ICESat-2数据与SRTM数据之间因时相差异或某些本文所没有考虑的隐含误差因素所造成的,在今后工作中,将进一步研究影响SRTM高程误差的因素,提高修正模型精度。
NOTES
*通讯作者。