1. 引言
随着网络技术的飞速发展,以及信息通讯技术的飞速发展,多媒体数据的传输已成为现代社会不可或缺的一部分。图像作为一种重要信息载体具有很多优点 [1] ,但也存在一些缺点。图像的可编辑性和真实性都可能导致其被篡改,伪造或者失真,降低了图像的可靠性;其次,图像中可以隐藏消息或数据,这可能导致潜在的安全隐患和隐私问题。因此,人们在使用图像作为信息载体时需要注意信息的完整性、真实性和安全性 [2] 。所以,随着量子计算和量子计算机等领域的迅速进展,确保数字图像信息传输的安全性日益凸显。近年来,量子图像处理技术持续不断地深入研究,保障量子图像的安全性成为一个不可避免的挑战。
2012年,Zhou等人提出了基于量子图像几何变换的加解密算法 [3] 。结合经典图像的几何变换,通过设计量子电路实现了量子图像的几何变换,并完成了量子灰度图像的加解密算法。该算法属于量子图像几何变换的应用,是量子图像密码学研究的新探索。2013年,Yang等提出的基于量子傅里叶变换(QFT)和双相位编码(DRPE)的灰度图像加解密方案 [4] 。该方案首次将双随机相位编码技术推广到量子场景,利用两个随机相位编码作为密钥,提高了方案的安全性。2014年,Song Xian-Hua等于2014年提出了基于受限几何和颜色变换的量子图像加密方案 [5] ,该方案主要是通过限制几何变换对像素位置编码进行置换该阶段的加密密钥由两个敏感混沌映射生成,具有高效的置乱效果。与之类似,2014年Wang Shen等提出了基于QWT变换与双扩散的量子图像加密方案 [6] ,其加密密钥是由敏感的混沌逻辑图生成。Hua等在2015年提出一种基于图像相关分解的量子图像加密算法 [7] ,该加密算法具有较大的密钥空间,能够抵抗蛮力攻击,同年,王申等人提出量子图像的最小有效量子位信息隐藏算法 [8] ,该算法设计了相应的幺正变换,以实现将秘密信息嵌入到代表量子覆盖图像颜色的最低有效量子位上。2016年,姜楠等在王申的基础上提出基于LSB的量子图像隐写算法 [9] ,推动了将秘密信息隐藏在量子图像等量子覆盖物中的技术的发展。
随着不断涌现出各种量子图像加密算法,多个量子置乱算法也已陆续被提出。在学术研究和理论的基础上,针对这些量子置乱算法,探索如何设计出处理速度更快,且置乱效果更好的方案是一个有价值的问题。量子图像置乱方案的改进对于量子图像水印、量子图像隐写等量子图像安全应用具有重要意义,这些改进的置乱方案可以显著增强图像的安全性,从而提高其保密性。图像置乱是图像加密的基本操作,通过改变图像的像素排列顺序来降低相邻像素值的相关性,使得图像呈现为一幅不具有明显意义的噪声图像。目前有两种主要的图像置乱方法。第一种是基于位置空间的置乱算法,其基本思想是通过改变图像的像素位置来破坏原始图像的信息。常见的置乱算法包括Arnold置乱算法,Fibonacci置乱算法以及正交拉丁方置乱算法等。第二种方法则是基于像素颜色的置乱,特别适用于量子图像加密。该方法的基本思想是破坏原始量子图像的颜色信息的统计特性,使直方图平滑,不再反映原始图像的信息,从而达到置乱的效果。目前这类置乱算法包括灰度编码置乱算法,通过位平面变换的置乱算法等。
量子Arnold置乱方法由于其较好的置乱效应而被广泛应用于量子图像加密,但是由于其自身的周期特性,经过多次迭代后,所得到的加密信息仍会被破解。因此,本文采用量子Arnold置乱与祖冲之序列加密相结合的方法,对量子图像置乱效果进行有效增强,提高其加密强度与安全性。基于量子Arnold置乱算法,祖冲之序列加密算法的知识,本文设计了基于祖冲之序列的量子图像加密算法,并对其算法复杂度进行分析,最后通过仿真实验展示和分析加密的效果。
2. 理论基础
2.1. 量子图像表示模型(FRQI)
2010年由Le等人首次提出了名为FRQI的表达式,它具有捕捉图像中每个像素点的颜色信息和对应位置信息的能力,借助量子叠加态来表示图像的信息,使其处于归一化的量子状态。公式(2.1)为FRQI整合为量子态形式,即
(2.1)
式中,
(2.2)
FRQI表达式使用
来表示原始图像的位置信息,且
包含了图像的横纵坐标信息 [10] ;公式(2.2)中,
与
表示为二维量子基态;
为对应颜色信息的角度向量,
。总而言之,FRQI表达式则涵盖了编码图像的颜色信息
和位置信息
这两个关键部分。
(2.3)
公式(2.3)中,前n个量子比特
编译图像纵坐标的位置信息,后n个量子比特
编译图像横坐标的位置信息。
假设FRQI图像大小为2 × 2,如图1所示,那么其对应的FRQI量子态表达式为 [11] :
在进行量子图像编译时,在量子计算领域,首要步骤是将计算设备初始化为所需的预备状态。这一初始过程是为了确保量子计算能够顺利进行。本文是通过使用Le等提出的PPT定理,将量子计算设备从初始状态演变为所需的图像表达式状态。
量子计算机从初始状态
转化为公式(2.1)所示的FRQI状态,其中关键步骤是通过酉变换完成的。具体的酉变换步骤如下:
1) 多项式数个Hadamard变换
使用Hardamard门将初始状态
转换为
,具体计算过程为
二维单位矩阵I和二维Hardamard矩阵表示为
(2.4)
将2n个Hadamard矩阵的张量积表示为
,在
上应用变换
来产生状态
,即
(2.5)
2) 利用受控旋转门,将量子计算机从初始化状态转换为FRQI状态
用旋转矩阵
将量子计算机从初始化状态
转换为FRQI状态
。
已知旋转矩阵
是沿y轴进行
角度旋转和受控旋转矩阵
得到的,其表达式如下:
(2.6)
(2.7)
将
和
应用于
,其表达式如下:
(2.8)
(2.9)
因此,从上式可以得到,
(2.10)
2.2. 量子图像置乱
图像置乱是指通过调整像素的位置,将图像呈现为不可读的形式,同时保持像素数量不变。在2014年,姜楠等研究人员首次提出并成功实施了基于量子图像的Arnold置乱、Fibonacci置乱以及Hilbert置乱技术 [12] ,以及它们的逆变换,这一突破代表了在图像处理领域的一项重要研究成果。前两者主要是基于量子加法器实现,后者是通过逐步迭代的方式实现。
量子Arnold置乱
Arnold置乱是建立在Arnold的遍历理论研究的基础之上的,作为其发展而来的一个重要理论成果。1992年,Dyson等研究人员将Arnold置乱方法成功应用于图像置乱领域。
表示原始图像
像素的位置坐标,
,这里假设图像大小为N × N,那么一个二维的Arnold置乱表示方法如下所示 [13] :
(2.11)
则
(2.12)
(2.13)
公式(2.10)中,
是Arnold置乱后图像的横纵坐标信息。其中,
为置乱矩阵。Arnold置乱的逆变换如下所示:
(2.14)
即
(2.15)
(2.16)
本文采用FRQI表示方法来描述图像,而量子Arnold置乱算法仅处理图像的位置信息,因此仅需在 FRQI表达方式中改变坐标信息
即可。在这里,我们定义了Arnold图像置乱操作为A,原始量子图像为I,
表示置乱后的量子图像,已知原始量子图像大小为2n × 2n,则
(2.17)
其中,
(2.18)
2.3. 祖冲之序列加密算法
祖冲之序列加密算法的结构可划分为三个主要组成部分。顶层是线性反馈移位寄存器(LFSR) [14] ,LFSR是一个寄存器序列,其根据预定义的反馈多项式进行位移操作。LFSR的作用是生成加密算法所需的伪随机序列,用于对原始数据进行扩散和混淆。第二部分是比特重组单元,是通过对LFSR输出序列进行重新排列和组合来进一步增加序列的复杂性和扩散效果。在第三部分,是对第二部分的比特数据进行非线性交换,主要采用S盒和高扩散特性的线性变换L,这一步骤旨在增强加密算法的输出,增加与密钥之间的复杂关系,从而提高安全性。
2.3.1. 线性反馈移位寄存器(LFSR)
LFSR主要包括两种模式,详细流程如下 [15] :
初始化模式下,将31比特数据流u作为输入,
,其中,W是非线性函数F的输出,F与
异或,得到的结果往右移一位,操作过程如下:
;
;
if
,then set
;
;
在工作模式下,LFSR停止接收任何输入信号,其操作方式具体描述如下:
;
if
,then set
;
。
2.3.2. 比特重组
比特重组是通过采用不同的置换函数或混淆操作,对LFSR序列的比特进行重新排列,具体是从以下的8个单元
进行重新组合,最终输出4个32位的字
,具体流程如下:
2.3.3. 非线性函数
W是一个32字的输出,通过非线性函数
计算得出,其中,
是非线性函数F的输入,详细步骤如下:
1) S盒
在非线性函数F中,S盒实现了非线性函数的作用。S盒是由4个8*8的S盒组成,即
,令
。
2) 线性变换函数L1和L2
在非线性函数F中L1和L2为两个线性变换函数:
3) 密钥扩展
密钥扩展的过程通常包括将初始密钥进行扩展和变换,以生成更长的密钥序列。
这里,初始密钥k和初始向量iv的长度均为128位,然而LFSR的初始状态是每31位16个单元,因此需要对密钥和初始向量进行扩展。
,
。D是常量,将D分为16组15比特的常量,则
,将
和
组合,得到LFSR的初值
,
。
3. 量子图像加密和解密方法
3.1. 量子图像加密
量子图像加密方法包括两个主要步骤。首先,以明文图像为输入,通过对其与以祖冲之序列生成的密钥序列进行加密分组链接模式的异或操作,获得相应的图像。其次,利用量子Arnold置乱方法对图像进行置乱,得到最终的密文图像。
3.1.1. 祖冲之序列加密算法
使用传统的祖冲之序列加密算法进行加密时,每个时序周期可以生成一个32比特的密钥,然后将这个密钥序列与明文图像数据信息进行按位异或操作。解密算法是将产生的密文图像与上述加密过程相同的密钥按位异或,从而还原出原始的明文图像信息。
为了提高图像的加密强度,本文采用加密分组链接模式进行加密。首先,对明文图像的数据信息进行分组,每32比特为1组。然后,引入初始化向量,并将第一组明文M1与初始化向量进行异或运算。接着,通过祖冲之序列加密算法生成的32比特密钥与异或结果进行加密,得到第一组密文C1。从第2组开始,将前一组的密文C1与当前明文M2进行异或,然后在进行加密得到密文C2 [16] [17] [18] [19] 。以此类推,直至加密完最后一组明文。图2展示了加密分组链接模式的加密过程。
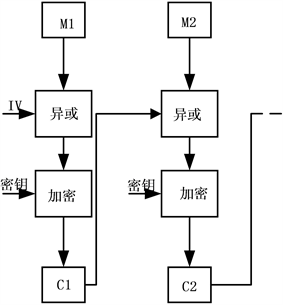
Figure 2. Encryption group link mode encryption process
图2. 加密分组链接模式加密过程
3.1.2. 量子Arnold置乱算法
采用量子Arnold算法对之前所述的祖冲之序列加密算法生成的加密图像进行置乱。首先,对图像进行预处理,分别提取图像的红色(R)、绿色(G)和蓝色(B)通道的像素值。然后,使用不同的密钥对每个通道进行独立的加密操作。最后,将三个通道分别加密后的图像合并,形成最终的密文图像。
根据(2.14)和(2.15)得Arnold图像置乱的量子表示方式,
(3.1)
(3.2)
即
(3.3)
3.2. 量子图像解密
Arnold算法在加密过程中是可逆的。祖冲之序列加密算法被归类为对称密码算法。因此,该算法的解密过程就是其加密过程的逆过程。下面是解密的详细步骤:将密文像素的位置信息
经过Arnold的逆置乱后得到
。
根据(2.14) (2.15)所示的Arnold逆置乱原理,可得
(3.4)
(3.5)
对第一组密文C1使用分组密码进行解密,然后将结果与初始向量IV执行按位异或操作,以获得明文M1。接着,再次使用分组密码对密文C2进行解密,随后与第一组密文C1执行按位异或操作,得到明文信息M2。这一过程可以连续进行,依次获得后续的明文M3、M4,一直延续到第n个明文Mn。如图3所示,这描述了加密分组链接模式的解密过程 [20] 。
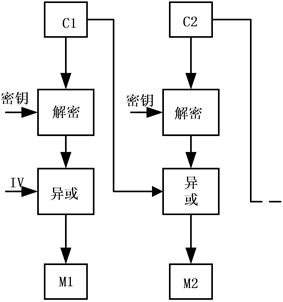
Figure 3. Encrypted group link mode decryption process
图3. 加密分组链接模式解密流程
4. 实验结果和理论分析
本节基于学术研究和理论,对上述加密方案进行了在经典计算机上的仿真实验,所有实验均采用Matlab R2022b进行实现 [21] ,实验用到的数据是经典图像Lena,图4展示了512 × 512大小的原始图像Lena,图5展示了加密后的图像,图6是解密后的图像。本文将从下面两方面来分析图像加密算法的效果。具体如下图所示。
4.1. 直方图分析
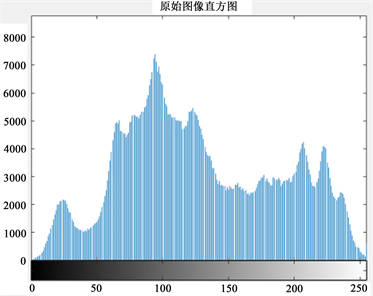
图像直方图描述了一幅图像像素值的分布状况 [22] 。图像在经过理想的加密算法后,密文图像的像素值会发生随机变化,使得原始图像的特征无法被直接观察到。密文图像的直方图分布越均匀,信号变得越随机,密文图像中明文图像的统计信息明显降低,加密后的图像越安全,从而可以抵御统计分析。下图7对比了原始图像和经过加密处理后的图像的直方图分布情况。研究结果表明,加密图像的直方图显示出了均匀的分布特征,波动在一定数值范围内 [23] 。这表明通过本文提出的加密方法后的图像抵御了直方图分析。
 (a)
(a)  (b)
(b)
Figure 7. Comparison of histograms between original image and cipher text image
图7. 原始图像和密文图像直方图对比图
4.2. 信息熵
信息熵是评估图像混乱程度的重要度量标准,其的数学表达式为 [24]
(4.1)
公式(4.1)中,
表示图像中的第i个像素位置;而
则表示该像素点在整个图像中的出现概率,且
。对于图像而言,理想的信息熵值应为8位,即每个像素点的分布应均匀 [25] 。从表1中可以看出,密文图像的R,G,B三个通道的信息熵分别为7.993,7.992和7.993,说明加密后图像的混乱程度大,表明通过采用该加密方案,图中的实验证据显示出其具备较高的安全性,并能够有效地抵御信息熵攻击。

Table 1. Comparison of information entropy of each channel in images before and after encryption
表1. 加密前后图像各通道信息熵对比
5. 结论
本文设计了一种基于祖冲之序列的量子图像加密算法,充分利用了祖冲之算法的高度安全性以及加解密操作的简便性 [26] ,提出了一种安全性高且高效的图像加密方法。其主要优点有两点:1) 祖冲之序列的快速性与资源节省性:该算法运行速度快,资源消耗较少,有效地提高了图像加密的速度。此外,它产生流式密钥时的快速实时性也大大增加了图像加密的效率。2) 分组链接模式的增强复杂性与随机性:在祖冲之序列加密过程中,采用了分组链接模式,通过按位异或操作,极大地提高了加密算法的复杂性和随机性 [27] 。通过进行仿真实验,结果表明本文提出的加密算法有效地减少了相邻像素之间的相关性。加密后的图像能够抵御直方图分析攻击,而且密文图像的信息熵接近8,表明具有高度的安全性,并且能够抵抗信息熵攻击。
基金项目
北京市教委科研计划项目(KM202010015009);北京印刷学院网络空间安全(数字版权保护技术)培育学科建设项目(21090123010);北京印刷学院青年卓越项目(Ea202411)。
参考文献
NOTES
*通讯作者。