1. 引言
随着锂电池体积增大、能量储存变高、使用环境变恶劣,电池因损坏而造成爆炸的隐患也在增加 [1] 。防爆片是电池的核心部件,具有安全阀门的作用,对其不规范的组装将直接影响到电池的使用寿命以及给使用者的安全带来隐患。目前生产线上一般采用人工检测防爆片的正反面并组装,不仅效率低、成本高、工作量大且长时间工作会给人眼带来一定的损伤。近年来迅速发展的机器视觉技术越来越广泛地用于产品检测 [2] [3] ;在机械臂原本集成技术的基础上,应用视觉定位技术,改变了传统机械臂单一、重复性的工作方式 [4] [5] 。
潘广耀等人 [6] 提出一种模板匹配与卡尺边缘拟合相结合的方法,实现目标工件精确定位与检测,但该方法需要提前制作工件的标准模板,如果模板不合格,即便获取的目标图像很清晰,该算法也无法准确识别目标信息。赵鹏宇等人 [7] 基于机器视觉技术提取目标图像的边缘特征从而达到识别工件的目的,通过定位工件的质心实现目标的定位,但忽略了提取不标准工件质心的难度。唐宇等人 [8] 提出基于区域划分识别平面工件的方法,该方法只适用于表面无遮挡的工件。
上述研究中只考虑解决目标定位不精确的问题,没有考虑对机械臂运行轨迹进行优化。因此,文中以防爆片为研究对象,通过视觉系统实现对工件定位与检测;采用7次B样条曲线完成机械臂轨迹规划,保证轨迹的高阶连续性和平滑性,同时采用NSGAⅡ-MOPSO混合算法对机械臂运行时间、能耗和轨迹冲击这三个目标同时优化,完成快速、稳定且无冲击的防爆片抓取搬运过程。
2. 防爆片自动摆盘系统设计
2.1. 系统结构
防爆片摆盘检测系统结构如图1所示,包括SCARA型机械臂、翻转装置、检测相机、定位相机、振动盘等。其中机械臂的夹爪采用如图2所示的双吸嘴吸盘,大大提升了系统的工作效率。
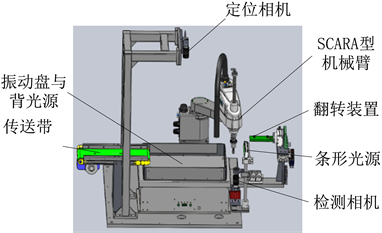
Figure 1. Structure of explosion-proof pieces automatic swing system
图1. 防爆片自动摆盘系统结构
2.2. 系统运行流程
首先传送带将防爆片运输到振动盘上,定位相机将振动盘上的防爆片信息反馈给上位机,上位机对防爆片图像进行识别定位,如果识别的目标都堆叠在一起,会给振动盘发送信号将堆叠的防爆片振散。之后机械臂将防爆片吸并取经过检测相机上方,检测目标的正反,如果检测结果为正,则将目标直接运送到下一工位的传送带上;检测结果为反则运输到翻转装置上,最后翻转转置旋转180˚将目标放入下一工位的传送带上。
3. 防爆片识别定位与正反检测
3.1. 防爆片识别定位
针对机械臂自身运动范围的限制以及防止机械臂与振动盘周围碰撞,对目标图像进行如图3所示的ROI目标区域选择。
由于采集的目标图像存在模糊、噪声等干扰,为了后续提高防爆片定位的准确性,需对图像进行预处理。图像预处理目的是为了去除噪声干扰、凸显目标区域以及增强相关信息的可检测性 [9] ,其主要步骤包括中值滤波、图像增强、形态学处理,图像预处理的效果如图4所示。

Figure 4. Blob analysis in the first nozzle region
图4. 吸嘴1区域Blob分析
本文采用Blob分析对防爆片进行定位,Blob分析是通过遍历行像素,将图像中具有相同像素的连通域划分,能够将目标从背景中分离出来,从而可以获得目标的数量、形状和位置信息,能够有效提高机器视觉算法的效率。Blob分析算法包括图像分割、形态学处理、连通性分析和特征提取等技术 [10] ,图4是对图3中的吸嘴一区域进行Blob分析,并通过设定连通域面积的阈值筛选出单个未堆叠的防爆片。最后获取图5所示的特征参数,图中防爆片的质心坐标是在像素坐标系中获取的,需要通过手眼标定将该坐标转换为机械臂基座标系中的坐标,机械臂的末端吸盘旋转角度与图中防爆片的角度相关,通过这些参数就确定了防爆片的位置信息。
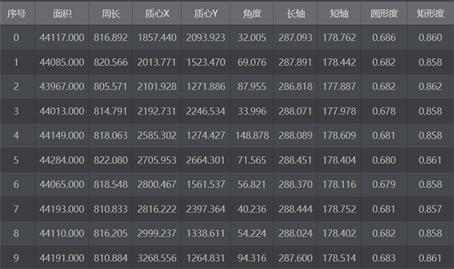
Figure 5. Characteristic parameters of explosion-proof pieces in the first nozzle region
图5. 吸嘴1区域防爆片特征参数
3.2. 单位防爆片正反检测
图6为检测相机拍摄的图像,其中左侧的防爆片为正面,可以看出上方ROI目标区域亮下方ROI目标区域暗;而防爆阀的反面则相反。因此可以通过求取两个ROI目标区域的灰度均值的差值来判断防爆片的正反。灰度均值的计算公式如下:
(1)
其中Mean为灰度均值;M × N为像素点总数;
为相应坐标处的灰度值。

Figure 6. Front and back detection of explosion-proof pieces
图6. 防爆片正反检测

Figure 7. Template matching of left explosion-proof piece
图7. 左侧防爆片模板匹配
由于系统存在误差,机械臂每次运行到检测区域的位置都会存在差别,这会造成选取的ROI目标区域的偏移,因此需要通过图像配准对图像中偏移的防爆片位置进行修正。当检测左侧防爆片的正反时,首先建立基准点,通过基于形状特征的模板匹配获取图7所示防爆片的匹配点像素坐标和角度,然后根据模板匹配结果中的匹配点与基准点的相对位置,通过式(2)进行仿射变换,实现防爆片位置的修正。右侧防爆片位置的修正也是如此。
(2)
其中(x, y)为原始坐标,(u, v)为变换后的坐标;tx表示图像在x方向上的平移量,ty表示图像在y方向上的平移量;θ则表示图像的旋转角度。
4. 基于时间、能耗和冲击的轨迹规划
4.1. 优化目标描述
防爆片识别定位完成后,机械臂则可以完成抓取任务,在满足机械臂自身约束的条件下,规划出一条理想的运行轨迹,该轨迹必须准确通过关键的目标点,且时间、能耗和冲击三个目标达到最优。根据多目标优化数学模型 [11] ,定义如下优化目标:
(3)
(4)
(5)
式中:T为机械臂运行轨迹一次的总时间;∆ti, ti, ti + 1分别为运行第i段轨迹的时长、起始时间和结束时间;ai, ji分别为第i个关节的加速度和加加速度;S1为运行时间,衡量机械臂的运行效率;S2为关节平均加速度,衡量机械臂关节的能耗;S3为关节平均加加速度,衡量机械臂关节的冲击与轨迹的平滑度。
构造机械臂关节轨迹时,需要考虑机械臂的位移、速度、加速度和加加速度等约束,即:关节位移
;关节速度
;关节加速度
;关节加加速度
。
4.2. 关节轨迹曲线的构造
在机械臂轨迹规划中,传统的高阶多项式插值 [12] 不具有局部可控性,不利于机械臂的运动控制。由于B样条曲线具有凸包性、局部支撑性等特性,故本文采用7次非均匀B样条曲线来完成机械臂关节轨迹的构造。B样条曲线 [13] 表现形式如下:
(6)
式中dj为控制顶点;Nj, k (u)为k次B样条的基函数;
为归一化时间向量;p(u)为时间u处的关节位置。
为了使机械臂轨迹经过目标点mPi,需通过目标点反求出B样条轨迹曲线的控制顶点。n + k个控制顶点di与节点矢量U可求解该B样条轨迹曲线,其中:
,
,对轨迹的时间节点ti归一化并使用累计弦长参数化方法得到内节点值:
(7)
其中
,
为弦长。由关节–时间变量列出n + 1个方程:
(8)
式中
。因此7次B样条需要增加k − 1即6个附加方程才能求解方程组,令机械臂始末速度、加速度和冲击为0得到6个方程,联立式(8)反求出控制顶点,再由控制顶点和时间节点矢量完成轨迹的构造。
4.3. 基于NSGAⅡ-MOPSO的轨迹优化
NSGA-Ⅱ与MOPSO算法都是仿生进化算法、全局优化算法、随机搜索算法、并行性算法。其中NSGA-Ⅱ算法拥有搜索能力强、鲁棒性好等优点;而MOPSO拥有搜索效率强、收敛速度快等优点。
针对上述两种算法的异同点本文提出NSGAⅡ-MOPSO混合算法,父代种群在同一次迭代中经过NSGA-Ⅱ和MOPSO算法分别生成种群大小为N的两个子代种群,然后合并子代种群与父代种群得到种群规模为3N的新种群,经过非支配排序,从新种群中选择N个合适的个体作为下一代父代种群,经过迭代后得到Pareto最优解集,该算法求解多目标轨迹优化问题的流程如图8所示。该混合算法扩大了搜索空间,加强了搜索深度,相较其中任意算法拥有更好的收敛性。
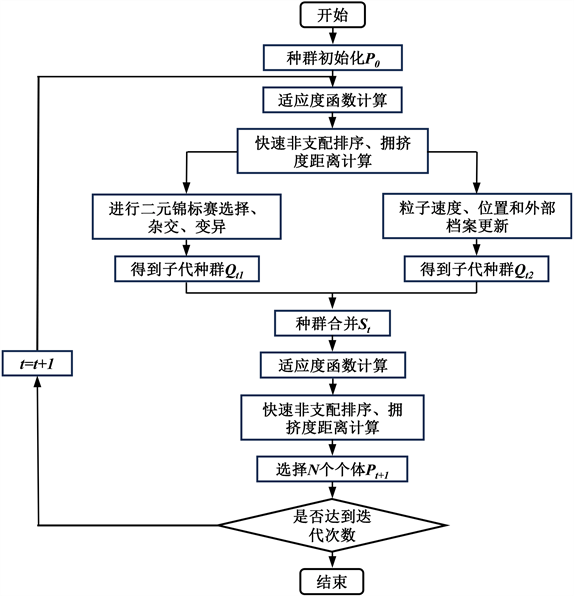
Figure 8. Process of solving optimal trajectory using NSGAⅡ-MOPSO
图8. NSGAⅡ-MOPSO混合算法求解最优轨迹流程
5. 实验结果及分析
5.1. 防爆片正反检测试验
为了检测该系统的准确性,在真实场景下对防爆片的正反进行检测实验,检测结果如表1所示。可以看出,该系统丝毫不受时间和工作量的影响,检测的准确率比较稳定,长时间工作下其准确率在98%以上,可以很好的代替人眼进行工作。

Table 1. Detection test of explosion-proof pieces
表1. 防爆片检测实验
5.2. 机械臂轨迹规划仿真
选取笛卡尔空间中的目标点作为SCARA型机械臂运动轨迹中经过的关键位置节点,通过逆运动学计算出关节空间各关节位置序列,表2为机械臂经过的关节位置序列。在如表3所示的运动学约束条件下,通过NSGAⅡ-MOPSO算法对机械臂的时间、能量消耗和机械臂冲击进行优化,得到各关节位置序列的最优点集。该算法的参数选择为种群规模200,交叉概率0.8,变异概率0.05,交配池规模100,迭代次数100,惯性常量0.5,局部学习因子1,全局学习因子2,杂交分布指数20,变异分布指数20。采用7次B样条构造关节轨迹,指定机械臂初始时刻的速度、加速度以及加加速度为0。
以S1时间、S2能耗和S3冲击作为优化函数,从图9可以看出NSGAⅡ-MOPSO算法的Pareto前沿的分布性较好且更加靠近原点,图中越靠近A点机械臂按轨迹运行一次时间越短,但机械臂的能耗和冲击越大;越靠近B点机械臂能量消耗和冲击越小,机械臂按轨迹运行一次时间越长。机械臂能耗与冲击大小是同向的,它们与运行时间大小反向。从图10看出基于NSGAⅡ-MOPSO得到的最优值优于其中任意一个单一算法,且混合算法有助于跳出局部最优。
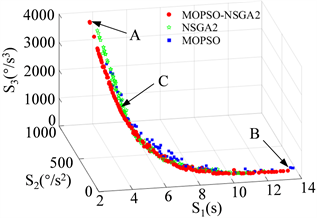
Figure 9. Pareto front surface of trajectory optimization based on different algorithms
图9. 基于不同算法的轨迹优化Pareto前沿面
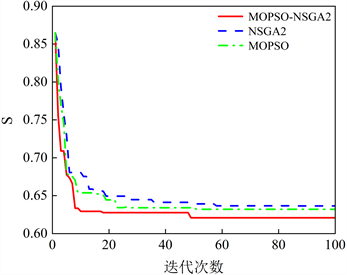
Figure 10. Pareto front surface of trajectory optimization based on different algorithms
图10. 基于不同算法的轨迹优化Pareto前沿面
表4给出了Pareto前沿上三个点的数据值。由于本文任务要求,对机械臂运行时间要求较高,采用加权目标函数方法得到图9上C点这个解,其中运行时间的权重为0.8、机械臂能耗和冲击的权重都是0.1。将C点作为机械臂轨迹优化的最终解,机械臂运行时间S1 = 4.1917s,关节平均加速度S2 = 304.6928˚/s2,平均加加速度S3 = 1501.1156˚/s3,优化出的时间节点向量Δt = [0.7786, 0.2361, 0.3753, 0.3447, 1.1546, 0.0411, 1.2584],优化前机械臂运行时间为6 s,优化后的运行时间比优化前的运行时间减少30%,得到图各关节的位移变化曲线如图11,其中图上的“”是机械臂通过的目标点。

Table 4. Trajectory optimal partial data of manipulator
表4. 机械臂轨迹优化部分数据点值
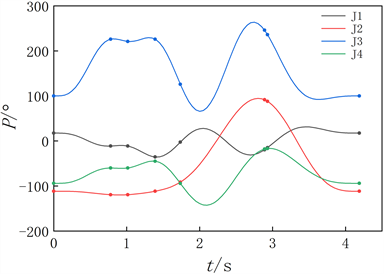
Figure 11. The trajectory curve of each joint of the manipulator
图11. 机械臂各关节轨迹曲线
图12给出了优化后机械臂各关节速度、加速度和加加速度曲线。从图中可以看出,采用7次B样条曲线,可得速度、加速度和加加速度稳定连续的轨迹且初始时刻速度、加速度和加加速度都为0。文献 [14] 采用5次B样条曲线构造关节运动轨迹并简单的将时间作为优化目标。而本文采用7次B样条作为运动轨迹,避免了5次NURBS曲线构造关节运动轨迹带来机械臂起停时加加速度不能自行指定的问题,这可能会引起机械臂起始时产生冲击造成机械臂振动的现象。NSGA-Ⅱ算法能实现机械臂多目标综合优化,在满足生产线对机械臂运行时间要求的同时,尽可能的降低机械臂的能耗和冲击。
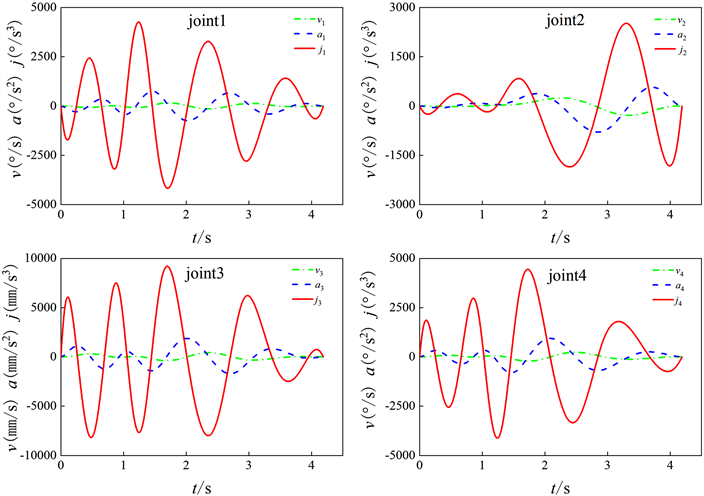
Figure 12. Velocity, acceleration and acceleration curve of each joint of manipulator
图12. 机械臂各关节速度、加速度和加加速度变化曲线
6. 结论
随着视觉的发展和应用,人工抓取工件逐渐被机器人替代。本文设计了防爆片自动摆盘系统,系统检测的准确率比较稳定,长时间工作下其准确率在98%以上。该系统采用7次B样条曲线作为机械臂关节的插值曲线,在运动约束的条件下,以运动时间、能耗、冲击作为优化目标,提出了NSGAⅡ-MOPSO算法并对机械臂的运行轨迹进行优化,该算法能够有效跳出局部最优,解决了NSGA-Ⅱ容易陷入早熟的问题,而且基于该算法得到的Pareto前沿面分布更加均匀,很好的提高了收敛速度。结果表明,提出的NSGAⅡ-MOPSO算法具有较高的实用价值,可以为机械臂高效、可靠、持久地作业提供指导。