1. 引言
在当今全球变暖和环境问题日益严峻的背景下,低碳制造成为了一种迫切的需求。据统计数据显示,中国制造业的碳排放始终占据总体碳排放量的60%以上,成为中国最大的碳排放来源之一 [1] 。中国政府在第七十五届联合国大会上宣布中国将提高国家自主贡献力度,采取更加有力的政策和措施,二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和 [2] 。因此企业走低碳制造之路,是当今社会可持续发展的必然选择。
在实现制造业节能减排过程中,识别并优化碳排放的集中环节是十分重要的。如何量化制造过程中的碳排放是优化加工参数的前提。李楠等 [3] 通过对比三个产品碳足迹国际标准,重点识别标准差异,并定性和定量解析了标准差异对于产品碳足迹的影响。杨云等 [4] 从能源、物料和废弃物三方面研究了车削加工过程中的碳排放组成,建立了车削加工过程碳排放计算模型。Li, W等 [5] 基于不同切削条件下的功率测量,从加工中的切削力以及加工参数对切削力的影响出发,建立了切削力对铣削与磨削加工的能耗影响模型,能够可靠地预测给定的工艺参数下的能耗。
切削参数的优化对降低加工成本和碳排放量也是至关重要的,Anand Y等 [6] 提出可使方差分析和响应面法去优化切削参数,采用HSS工具进行加工,并对不同材料切削参数的变化结果进行了研究。He Bin [7] 等考虑了切削参数或生产调度之间的耦合关系,在选择算子中引入Crowding Niche机制和精英保留策略,改进基于Pareto最优的遗传算法,实现了模型的多目标优化。詹欣隆等 [8] 将切削参数与调度方案之间进行集成结合,通过对比改进的非支配排序遗传算法和离散化引力搜索算法,求解了机器切削参数与调度方案之间的协同优化问题。尹瑞雪等 [9] 考虑机床性能参数和加工质量等约束,建立了数控车削切削参数优化模型,并利用遗传算法得到了合理的切削参数优化。
针对上述问题,本文综合考虑机床、刀具性能约束,建立了车削过程中以碳排放最低、加工成本最少为目标的工艺参数优化模型,最后运用改进的鲸鱼优化算法对所建模型进行寻优求解,并结合实例验证所建模型的有效性。
2. 销轴加工工艺参数优化模型建立
2.1. 选择优化变量
在数控车削加工过程中,为实现高效低碳制造,合理设定加工工艺参数具有关键性的影响。目前影响碳排放和加工成本的主要工艺参数为车削速度、进给量、切削深度,因此本文设定优化变量为车削速度vc、工作台进给量f以及背吃刀量ap。
2.2. 优化目标函数
优化目标函数需要综合考虑多方面因素和约束条件,并通过调整自变量的取值来寻找最优解。在双碳目标的背景下,车削加工时有效控制机床设备的碳排放是极为重要的。并且在企业层面,加工过程的生产成本也是亟待改善。因此,本文主要以碳排放量和加工成本作为优化目标。
2.2.1. 车削加工过程碳排放函数
数控车削加工过程的碳排放主要由坯料制备、机床能耗、刀具磨损、车削液碳排放和附属设备能耗(冷却系统、空压机、除尘设备等)组成。由于坯料制备中的加工工序是已设计好的,后面对其碳排放的优化有限,并且附属设备能耗的碳排放在一定程度上也可以视为稳定不变,为简化模型,因此只考虑余下几者的影响。本文就车削参数对碳排放的影响,确定车削加工的总碳排放量Cg中包括车削碳排放Ce和辅助碳排放量Cm,得到机床车削加工过程的碳排放公式如下:
(1)
(1) 车削加工过程碳排放
车削加工过程的电能耗Ee包括空载过程能耗Em,kW·h;车削过程能耗Ec,kW·h和附加载荷能耗Ea,kW·h。由文献 [10] 得知,当主轴没有切削负载时,在转速和负载恒定的情况下空载功率、切削功率和附加载荷功率也是一恒定值(在实际中可能会有微小波动,可忽略不计)。因此可列出公式:
(2)
式中:Pm为机床空载功率,kW;Pc为机床车削功率,kW;Pa为附加载荷功率,kW;t1为机床切削的总时间,其中包括了车削部分的时间t2;t3为附加载荷损耗的时间,且附加载荷是由车削加工引起,故t3 = t2。
机床的空载功率Pm为:
(3)
式中:Pm0为机床最低空载功率,kW;n为主轴转速;K1、K2为机床主轴转速系数。
机床的车削功率Pc参考文献 [11] 可得出下式:
(4)
由于Ff消耗的功率不足总功率的1%,故可以忽略,进而得出下式:
(4)
(5)
式中:Fc为车削力,N;vc为车削速度,mm/s;
、
、
、
、
为与车削加工有关的系数。
机床的附加载荷功率Pa参考文献 [12] 得出为:
(6)
式中:be为附加载荷损耗系数,取值范围在0.15~0.25之间。
为进一步便捷的对机床车削过程能耗进行评估预测,需要对函数变量简化处理:
(7)
其中:d0为刀具直径。
最后机床车削过程能耗模型可简化如下:
(8)
上式与碳排放因子Fe相乘即为车削加工过程碳排放,如下:
(9)
(2) 辅助碳排放
辅助碳排放指的是与机床车削过程相关的其他碳排放,其中涉及到与本文车削参数优化相关的主要为刀具碳排放和车削液使用碳排放,为简化计算,本文的辅助碳排放只计入这二者。
刀具碳排放Ct是指刀具在加工过程中损耗导致的碳排放,其大小如下:
(10)
(11)
其中:Ft为刀具的碳排放因子,kgCO2/kg;Mt为刀具质量;N为刀具生命周期中包含的重磨次数;Lt为刀具耐用度;cf,x,y,z均为与刀具寿命有关的系数。
车削液(生产中常用水溶性车削液)碳排放Cf主要由两边部分组成:配置车削液所需纯矿物油的制备引起的碳排放Cp以及废车削液处理引起的碳排放Cw。再查阅 [13] ,可得到纯矿物油的制备的碳排放因子Ep和废车削液处理的碳排放因子Ew,进而可得出下式:
(12)
(13)
(14)
其中:Tf为车削液更换周期;V0为原始车削油用量,L;Va为附加车削油用量,L;Ep为车削油制备过程的碳排放因子,kgCO2/L;Ew为废弃车削液处理碳排放因子,kgCO2/L;
为车削液浓度。
2.2.2. 车削加工过程成本函数
在数控机床的车削加工过程中,加工成本主要有能耗成本、车削液成本、刀具成本和机械设备折旧成本。
(15)
(1) 能耗成本主要包括车削过程中数控机床的能耗以及辅助设备的能耗,而由于辅助设备能耗受加工参数的影响较小,为简化计算,可不计入成本,因此可得出能耗成本如下:
(16)
式中:Et为机床车削加工过程总能耗,kWh;pe为电能单价,元/kWh。
(2) 车削液成本包含了车削过程中定期补充的车削液成本和废车削液处理成本。
(17)
式中:pa为单位车削液铣削成本,元/L。
(3) 刀具成本为实际车削过程中刀具磨损导致的成本。
(18)
式中:pt为刀具价格,元。
(4) 机械设备折旧成本为:
(19)
式中:pla为数控机床成本,元;Tla为数控机床的使用寿命,min。
2.3. 约束条件
(1) 最大功率约束:
在车削加工过程中,车削功率不能超过机床主轴电机的最大功率Pmax:
(20)
式中:
为机床效率系数。
(2) 最大切削力约束:
车削过程中的切削力不能超过机床额定的切削力Fmax:
(21)
(3) 车削转速约束:
(22)
式中:D为待加工面直径,mm;nmin、nmax分别为机床的最小转速和最大转速,r/min。
(4) 进给量约束:
(23)
式中:fmin,fmax分别为机床最小进给量和最大进给量。
(5) 工件表面粗糙度约束:
(24)
式中:Ra为零件表面粗糙度,rg为刀尖圆弧半径,Ramax为零件表面要求的粗糙度最大值。
3. 基于改进鲸鱼优化算法的模型求解
3.1. 多目标函数转化
基于碳效益的切削参数优化问题实质上是一种多目标优化问题,往往很难同时达到各个目标的最优解。因此本文采用权重系数法,将多个目标聚合成一个综合指标,从而转化为单目标函数:
(25)
其中:w1、w2均为权重系数,本文将碳排放量和车削加工成本的重要性视为相等,则可确定w1 = 0.5、w2 = 0.5。
对碳排放目标函数和加工成本目标函数求和前需要进行量纲统一化处理:
(26)
(27)
其中:
表示量纲统一化后的Cg;
表示量纲统一化后的Pg;Cgmax、Cgmin分别是碳排放函数在约束条件下的最大值和最小值;Pgmax、Pgmin分别是加工成本函数在约束条件下的最大值和最小值。
量纲统一处理后的单目标函数为:
(28)
3.2. 标准鲸鱼优化算法
鲸鱼优化算法(Whale Optimization Algorithm, WOA)是由Mirjalili [14] 等提出的一种新的群体智能优化算法,其灵感来源于鲸鱼的迁徙行为。鲸鱼优化算法具有高效性、简单性、灵活性、全局性和鲁棒性较好的优点。这种优化算法模拟了鲸鱼在寻找饵食时的集群行为,通过个体的协作与竞争来寻求最优解。该算法的基本思想是利用鲸鱼族群中的个体行为来搜索最佳解决方案。初始时,个体们根据自身的位置和适应度值进行搜索,并被分为不同的群体。然后,通过交叉和变异操作来调整个体的位置,模拟了鲸鱼的迁徙行为和对环境的适应能力。这样一步步的迭代过程将逐渐收敛到最优解,其原理如下:
(1) 初始化鲸鱼种群:
(29)
其中:Xi为鲸鱼个体i的位置;ub和lb为搜索空间的上界和下界;rand为(0, 1)的随机数。
(2) 包围猎物:
(30)
其中:t为当前迭代次数;Xe(t)表示当前鲸鱼的最优位置;r1和r2为(0, 1)的随机数;收敛因子α在迭代的过程中逐渐从2下降至0,即:
(31)
其中,tmax为最大迭代次数。
(3) 气泡网捕食:
收缩包围:通过减小公式(31)中的收敛因子α来实现。
螺旋更新:
(32)
其中:Dp表示第i个个体与最优个体之间的距离,b为用来定义螺旋线形状的常数,l为[−1, 1]之间的随机数。
为了同时模拟鲸鱼捕食过程中的收缩包围机制和螺旋更新机制,假设这两种机制执行的概率p相等,其数学模型可表示如下:
(33)
(4) 随机更新:
当A的绝对值大于1时,鲸鱼会远离目标猎物,根据彼此之间位置进行随机搜索,相当于探索阶段,这样可以加强算法的探索能力使得此算法能够进行全局搜索,具体公式如下:
(34)
(35)
其中:Xrand是随机选择的鲸鱼位置向量。
3.3. 算法改进
传统鲸鱼优化算法在解决一些复杂的非线性优化问题时存在着容易陷入局部最优解、缺乏多样性并且收敛速度较慢等问题。为了克服这些缺点,本文引入了精英反向学习的方法来提高种群的多样性,并采用非线性收敛因子来改善算法的收敛性。此外,还引入了高斯随机游走策略,以避免陷入局部最优解,具体改进方法如下:
(1) 精英反向学习选择精英个体。
在传统鲸鱼优化算法中,可以引入精英反向学习机制 [15] 。该机制的目标是对当前种群中的精英个体进行学习和改进,通过传递精英个体的信息来加速收敛,保留一定的随机性,用以确保种群的多样性。
(36)
其中:L和U分别为可行解上下界;R为(0, 1)内的动态随机参数。
(2)
转为非线性收敛因子。
为了提高算法的收敛性能,可以将
转为非线性收敛因子。该因子可以动态地调整算法的收敛速度,使算法在开始阶段具有较快的收敛速度,在接近最优解时逐渐减小收敛速度,以避免过早陷入局部最优解。
(37)
(3) 高斯随机游走策略。
为了增加算法的探索能力,可以使用高斯随机游走策略 [16] 。该策略可以在搜索空间中引入一定程度的随机性,它可以使鲸鱼个体以一定的概率朝着随机方向移动,从而更好地探索未被访问的解空间,并有机会跳出局部最优解。
(38)
(39)
其中:
是产生一个以
为均值;
为方差的随机数;
和
分别为在第t次迭代中的最优个体和第i个个体;r3和r4为服从(0, 1)之间均匀分布的随机数。
3.4. 改进鲸鱼优化算法的步骤
改进后鲸鱼优化算法的步骤如下:
步骤1:确定种群个数N,最大迭代次数tmax,空间维度dim,螺旋形状常数b = 1,以及一些算法参数。
步骤2:初始化种群,使用(29)初始化鲸鱼种群Xi,并计算个体的适应度值。
步骤3:用精英反向学习策略优化初始化种群,并计算个体的适应度值,并与之前比较,保留较优值。
步骤4:根据不同的参数值选择不同阶段的位置更新,当p < 0.5时,若是|A| < 1,则选用公式(38)更新鲸鱼个体位置;若|A| ≥ 1,则选用公式(30)更新鲸鱼个体位置,并计算个体的适应度值。
步骤5:当p ≥ 0.5时,选用公式(32)更新鲸鱼个体位置,并计算个体的适应度值。
步骤6:判断迭代次数是否达到最大迭代次数tmax,若未达到,则先用公式(37)更新α,A,C,再返回步骤(4)继续优化搜索;若达到,则输出最优个体位置和适应度函数值。
4. 实例分析
4.1. 实验模型参数
以CK6130数控机床(规格参数如表1所示,机床折旧费按200元/h计算)车削加工某型号的销轴为例(零件材质为45号钢,尺寸参数如图1所示),分析验证优化方法的可行性和效果。

Table 1. CK6130 CNC lathe standard parameters
表1. CK6130数控车床标准参数
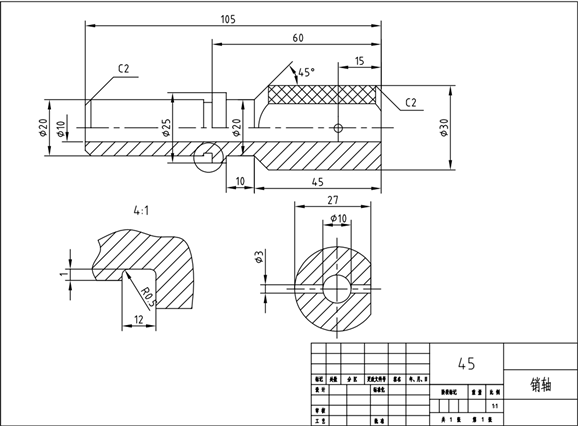
Figure 1. Dimensional drawing of pin shaft parts
图1. 销轴零件尺寸图
零件未优化前单边切削加工安排为:2次粗加工和2次精加工,前两次粗加工和后两次精加工的切削深度分别为:4.0 mm、2.5 mm、1.0 mm和0.5 mm。将切削参数带入模型可得出其碳排放量和加工成本,原始切削参数如表2所示,切削力相关参数见表3。

Table 2. Original cutting parameters
表2. 原始切削参数

Table 3. Coefficients of cutting forces
表3. 切削力相关参数
加工工具为硬质合金车刀,加工要求达到的表面粗糙度为Ra= 6.4 µm,刀具碳排放相关参数见表4。加工过程需使用车削液,车削液碳排放相关参数见表5。

Table 4. Parameters related to carbon emissions of the cutting tool
表4. 刀具碳排放相关参数

Table 5. Parameters related to carbon emissions of the cutting fluid
表5. 车削液碳排放相关参数
4.2. 实验结果及分析
根据上述两种算法的基本步骤编写相应的程序,用Matlab2019a软件进行仿真运行。设置种群规模为100,迭代次数为150。实验结果如图2所示。
从图2结果中分析,传统WOA算法虽然在迭代初期收敛速度较快,但是在迭代次数为40代左右开始收敛,很快就陷入局部最优解,不再随着迭代次数增加而优化。改进后的WOA算法在搜索最优解的过程中会朝着更优化的方向前进,逐渐接近最优解,在取得更小的最优解的同时避免了传统鲸鱼算法早熟收敛的问题,相比之下有比较好的改善。由改进的WOA算法搜索到的优化结果如下表6所示。
在优化过程中,我们设置了精加工次数和刀具背吃刀量不变,以确保零件表面粗糙度达到要求。排除掉由废屑等材料引起的固定碳排放,每次联轴器切削加工所产生的最小碳排放量为105.3克。通过对比表2和表6可知,相较于原先的碳排放量125.6克,这一数值降低了16.1%。我们采用了优化后的加工参数进行车削加工,得到的成本为5.06元。与原先的成本6.52元相比,降低了22.3%。这证明了本文所提出的优化模型以及改进后的WOA算法的有效性,以及达到了优化的效果。
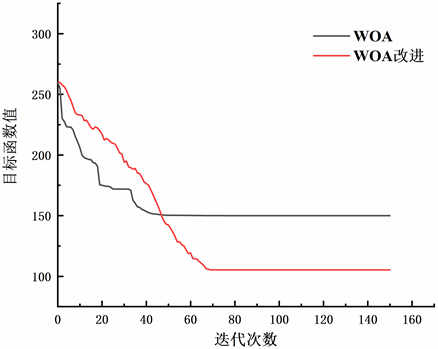
Figure 2. WOA, improved WOA algorithm
图2. WOA、改进WOA算法

Table 6. Optimized turning process parameters
表6. 优化后的车削工艺参数
5. 结论与展望
本研究建立了针对销轴车削加工的基于低碳的车削参数优化模型,考虑了各因素对碳排放和成本的影响,并基于机床性能、最大切削力和表面粗糙度等约束条件进行了分析。通过对鲸鱼优化算法的三方面改进,并以一个具体实例为例,采用改进后的算法对模型进行求解,结果显示最大可降低碳排放量16.1%和加工成本22.3%。然而,由于销轴制造涉及多个工序,本研究仅对车削加工工艺参数进行了研究,其他工序的切削参数优化仍需要进一步研究。
基金项目
浙江省2023年度“尖兵”“领雁”研发攻关计划(2022C01SA111123);国家自然科学基金资助项目(51475434)。