基于OD识别和客流预测的城市公共交通多源数据分析关键技术研究

Research on Key Technologies of Multi-Source Data Analysis of Urban Public Transport Based on OD Identification and Passenger Flow Prediction

摘要: 随着城市公共交通体系的逐步完善，通过大数据等新兴技术手段，深入研判和预测公共交通客流情况至关重要。目前公交OD (origin-destination)识别效率及预测效率都比较有限，客流分配不够合理，无法有效支撑公交出行特征分析、公交专项规划管理等，亟需从理论和实践出发，开展进一步的深入研究和探索，因此需要对现有技术进行改良。本文结合大数据及机器学习等，对公共交通数据进行分析，首先结合Transcad最短路径方法对公交OD识别算法进行优化，其次分别采用五种模型构建公交短时客流预测算法并进行对比分析。结果表明本文在优化公交OD识别算法后，算法效率上有较大提升，同时公交短时客流预测中Tensor + ARIMA方法在效率和精度方面表现较好，能够更好地适用于该领域的实践应用。

Abstract: With the gradual improvement of the urban public transportation system, it is crucial to study and predict the public transportation passenger flow in depth through big data and other emerging technical means. The current public transportation OD (origin-destination) identification efficiency and prediction efficiency are relatively limited, and the passenger flow distribution is not reasonable enough to effectively support the analysis of public transportation travel characteristics and public transportation special planning management, etc. Further in-depth research and exploration are urgently needed from theory and practice, so the existing technology needs to be improved. This article combines big data and machine learning techniques to analyze public transportation data. Firstly, it optimizes the public transit OD identification algorithm by integrating Transcad’s shortest path method. Secondly, it constructs five different models to develop short-term public transportation passenger flow prediction algorithms and compares them. The results show that after optimizing the public transit OD identification algorithm, there is a significant improvement in algorithm efficiency. Additionally, the Tensor + ARIMA method performs well in terms of efficiency and accuracy for short-term public transportation passenger flow forecasting, making it more suitable for practical applications in this field.

1. 引言

随着城市公共交通体系的逐步完善，通过大数据等新兴技术手段，深入研判和预测枢纽出行特征至关重要。目前在公共交通出行方面，受多模式换乘、单次售检票、多渠道支付等因素影响，尚存在公交OD识别率低、预测精度有限、客流分配结果与实际相差甚远等诸多问题，无法有效支撑公交出行特征分析，公交专项规划管理等，亟需从理论和实践出发，开展进一步的深入研究和探索。

在公交OD识别方面，国内主要围绕IC卡刷卡记录、公交GPS(全球定位系统)等相关数据进行研究，主要涉及乘客公交出行的上下站点识别 [1] [2] [3] 和公交出行OD矩阵的推导 [4] [5] [6] [7] 等。国外主要围绕挖掘IC卡数据以及利用其推导公交OD矩阵等方面进行研究 [8] [9] [10] [11] [12] 。

在短时交通流预测方面，国内外通常采用线性回归 [13] 、卡尔曼滤波法 [14] 、人工神经网络 [15] [16] 等模型进行研究。因为短时客流预测对样本信息和预测精度的要求较高，近些年国内外非常注重对组合预测方法的研究 [17] [18] [19] [20] ，并研究出了一系列成果。

本文应用多源大数据融合分析、人工智能机器学习等新兴技术，突破城市综合交通枢纽出行定量分析中的公交OD识别、多方式短时预测两大技术瓶颈，并且本文将扬州市公交数据作为案例对模型进行了精度校核和有效性验证。

本文的贡献总结如下：1) 基于多源数据的公交出行特征分析技术；2) 基于机器学习的分方式客流短时预测技术。

2. 数据库构建

为了便于数据输入输出和后续项目研究，设计了一套公交数据库标准，包含原始数据表、中间数据表、指标数据表三类。数据从扬州市公交数据中选取。

原始数据表包括公交设施类、公交需求类以及公交运行类。公交设施类包括分方向公交线路表、公交站点表、道路路段表和道路节点表。公交需求类包括巴士交易数据表记录乘客刷卡信息。公交运行类包括巴士GPS表存储轨迹信息。

中间数据表包括公交设施类、公交需求类以及公交运行类。公交设施类包括同线路公交站间成本表、公交站间路径表和公交站间最优路径表。公交需求类包括同线路巴士出行表配对和公交出行表。公交运行类包括巴士班线表用于存储巴士到达、离开各站点的时间。

指标数据表包括公交需求类以及公交运行类。公交需求类包括公交站间出行客流表和公交小区出行客流表。公交运行类包括公交站点客流指标表、公交线路客流指标表、公交网络客流指标表、公交站点换乘客流表和道路运行指标表。

3. 公交OD识别算法

为方便管理各类数据表，基础数据存储采用SQL Server、算法处理采用Python语言编程(Pandas、Geopandas、Numpy数据模块等)、交通OTD (出发地–出行方式–目的地)识别采用Transcad最短路径方法。本节输入数据为公交线路走向、物理站点、GPS及交易原始数据；输出数据为公交OD、线路、站点、断面等多维度客流指标。

3.1. 建立地图数据

本小节利用公交站点GIS (地理信息系统)输入物理站点表、线路线位表以及线路属性表，将物理站点转换为线路站点(不分方向)，并将垂足坐标加入线路轨迹列表以更新公交站点地理信息数据表，最终的公交站点地理信息数据表如表1所示。并利用垂足坐标和站点间直线距离矩阵，输出站间距离表以及步行换乘表。得出的结果利用高德地图进行数据校核，站点基本无缺漏，匹配率较好。

Table 1. Example of a transit stop geospatial data structure

表1. 公交站点地理信息数据结构示例

3.2. 乘客上车站点识别

首先对车辆GPS数据进行清洗。接下来将GPS数据与公交站点GIS数据进行关联匹配，根据经纬度来确定公交车辆与公交站点之间的空间距离 [8] ：

$d=R\ast \arccos \left[\sin \left({\text{Lat}}_{\text{GPS}}\right)\ast \sin \left({\text{Lat}}_{\text{GIS}}\right)+\cos \left({\text{Lat}}_{\text{GPS}}\right)\ast \cos \left({\text{Lat}}_{\text{GIS}}\right)\ast \cos \left({\text{Lon}}_{\text{GPS}}-{\text{Lon}}_{\text{GIS}}\right)\right]\frac{\pi }{180}$ (1)

式中，R为地球半径，取6,371,004 m，d为站点与车辆的空间距离，Lon_GPS为公交GPS轨迹信息表中Lng的值，Lat_GPS为公交GPS轨迹信息表中Lat的值，Lon_GIS为GIS中的公交线路站点的经度字段的值，Lat_GIS为GIS中的公交线路站点的纬度字段的值。

GPS数据的记录的时刻并不一定是真实的公交进站时刻，因此需要设置一个空间误差范围，即以公交站点经纬度位置为圆心，设置误差半径LZ的圆形识别区域(简称缓冲区)，一般可设为公交站点沿道路方向的最大长度(一般可设为30 m)，若存在落在缓冲区的GPS数据记录点，且该记录点的速度值小于设定的速度阈值VZ (一般可设为3 km/h)，同时满足车辆行驶方向角与站点方向角差值的绝对值 ≤ 60时，可确定该记录点为特征点，即为有效进站点。

若公交站点识别区域内没有特征点，则寻找同一线路上距离站点最近的两个记录点，可以假设公交在两点间匀速运行，通过记录的车辆位置坐标得到这两点间的公交线路长度d_z和它们分别与该站点间的线路长度d₁和d₂，与两点的记录时刻t₁和t₂，可知两点间假定的匀速运行速度 $\overline{\stackrel{¯}{V}}$ 为：

$\overline{\stackrel{¯}{V}}=\frac{d_z}{\left|t_1-t_2\right|}$ (2)

从而得到公交进站的近似时刻 ${\overline{\stackrel{¯}{t}}}_z$ 为：

${\overline{\stackrel{¯}{t}}}_z=t_1+\frac{d_1}{\overline{\stackrel{¯}{V}}}$ (3)

或反方向为：

${\overline{\stackrel{¯}{t}}}_z=t_2+\frac{d_2}{\overline{\stackrel{¯}{V}}}$ (4)

由于特征点的速度值最小，所以可认为特征点记录的时刻极其接近进/出站时刻。在无法确定车辆进、出站时刻的情况下，以特征点记录时刻为区间中心，车辆的最大驻站时间为区间半径，构造出一个驻站识别区间(缓冲区)。当特征点记录时刻为 $t_z$ ，车辆最大驻站时间为 $t_{s\max }$ (一般设为30 s)，则驻站识别区间为 $\left(t_z-t_{s\max },t_z+t_{s\max }\right)$ 。同理，跳站情形下，被跳站点的驻站识别区间为 $\left({\overline{\stackrel{¯}{t}}}_z-t_{s\max },{\overline{\stackrel{¯}{t}}}_z+t_{s\max }\right)$ 。

对公交IC卡消费记录进行清洗。关联GPS数据与公交站点GIS信息，得到GPS数据相对应的公交站点，然后匹配GPS数据和IC卡消费记录，得出乘客的上车站点。

3.3. 乘客下车站点识别

首先针对城市公交线路设置一个空间判断阈值，取两个相邻公交站点间的最大距离，用l_om (一般为200 m)表示。根据前后两次乘车过程的公交IC卡刷卡记录来判断这两次公交出行是否构成空间衔接，判断依据为：若以后一次乘车过程的上车站点为圆心，l_om为半径的圆形区域内存在至少一个属于乘客前一次乘车过程乘坐的公交线路的上车站点在其线路运行方向上的后继站点，则认为这两个公交乘车过程可以在空间上构成衔接；反之则不构成衔接。

假设乘客一天中所有公交乘车过程所对应的车辆运行情况如图1所示。根据判断逻辑，可认为在站点A上车的乘车过程与在站点B的乘车过程可能构成衔接，并且站点S1和S2可能为第一次刷卡记录的乘车过程的下车站点。依次类推，站点C、D刷卡记录的乘车行程同样可以判断是否会在空间上有衔接。

在设置空间判断阈值的基础上，还需要添加时间判断阈值。只有两者都满足的情况下，才能判断两次乘车行为构成时空上的衔接。具体来说，乘客在站点A上车的乘车过程与在站点B的乘车过程在判断是否形成空间衔接后，还要判断乘客在站点S1或站点S2下车的不同情况下，分别到达站点B的时刻。

假设乘客在站点B的上车刷卡记录时刻为t，乘客在站点A乘坐的车辆到达站点S1与站点S2的特征点记录时刻分别为t₁和t₂，站点S1、S2与站点B的距离分别为d₁和d₂，另设v_max为人的最大步行

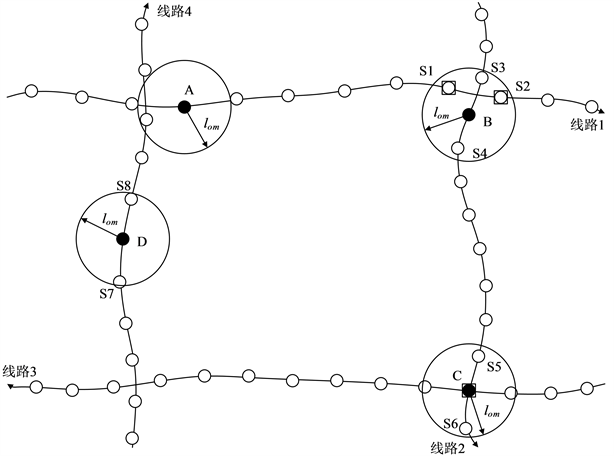
Figure 1. Spatial relationship between front and rear passes

图1. 前后两次乘车空间关系图

速度，一般设为1.5 m/s，t_cm为同一站点经过的相邻的两辆同一线路不同班次的公交车的最大间隔时间，一般设为10 min，作为公交出行链上的时间判断阈值。定义 $\left(t-t_{cm},t\right)$ 为换乘行为的判断区间，如处于早晚高峰期，该区间可以扩大 $\left(t-2t_{cm},t\right)$ 。通过上述定义，可做出如下分析，乘客从站点S1、S2下车后前往站点B的到达的具体时刻分别为 $t_1+d_1/v_{\max }$ 和 $t_2+d_2/v_{\max }$ 。通过判断到达时刻与区间的关系，可分辨出下车行为和换乘行为。

因此结合具体情况，可得换乘与下车站点的识别过程如下：

(1) 若之前没有匹配出上车站点，则下车站点无法确定。

(2) 若之前匹配出上车站点，且乘客当天只有一次乘车刷卡记录，则无法确定该记录对应的下车站点。

(3) 若乘客在同一个站点连续刷卡，可能存在代替他人刷卡行为，则无法确定被代替刷卡的乘客下车站点。

(4) 若乘客当日最后一次刷卡记录所搭乘的线路，就是当日最早搭乘的线路。则分如下几种情况：① 如果两次乘车方向相反或者为循环线，那么该记录对应的下车站点是当前线路上距离当日最早乘车站点最近的站点。② 如果两次乘车方向相同或者为非循环线，那么该记录对应的下车站点是当前线路上距离次日最早上车站点最近且小于l_om的站点。

(5) 若乘客当日最后一次刷卡记录中所搭乘的线路与当日最早搭乘的线路不同，那么该记录对应的下车站点是当前线路的当前方向上与当日最早乘车站点距离最近且小于l_om的站点，如果没有这样的站点则无法确定该记录对应的下车站点。

(6) 若乘客当前乘车的站点与下一次刷卡记录中乘车的站点不同，且非前五种情况，那么当前乘车过程的下车站点是当前线路的当前方向上距离下一次刷卡的站点距离最近且小于l_om的站点。

(7) 在(6)的基础上，区分下车行为与换乘行为：① 当乘客到达下次乘车站点的时刻在换乘行为定义区间内时，可认为当前下车站点为换乘站点。② 当乘客到达下次乘车站点的时刻在换乘行为定义区间的左侧时，可认为当前下车站点为普通的下车站点。③ 当乘客到达下次乘车站点的时刻在换乘行为定义区间的右侧时，可认为这两次公交乘车过程在时间上不衔接，无法形成出行链。乘客到达下一个乘车站点的时刻如下：

$t_d=t_u+\frac{d}{v_{\max }}$ (5)

其中t_u为车辆到达当前下车站点的时刻，t_d为乘客到达下一个乘车站点的时刻，d为从当前下车站点到下一次乘车站点的距离，v_max为人步行的最大速度。

在判断出下车及换乘行为后，需要在已匹配的上/下车站点中，去除那些已被确定为换乘行为所对应的站点，以明确乘客公交出行的真实目的地/出发地。

整体算法流程下所示：

STEP 01：对乘客刷卡数据进行出行时间聚类，30天内出行天数 ≤ 9的乘客定义为低频乘客，出行次数 > 9的乘客定义为高频乘客。

STEP 02：对乘客上车站点进行匹配，统计乘客当天的出行距离和出行时间，是否满足出行链在空间和时间的阈值范围。

STEP 03：若乘客当天存在出行链，通过乘客刷卡时间差或换乘距离作为判别换乘的约束参数，来判断真实出行起点、换乘、终点；若乘客当天不存在出行链，高频乘客下车站点根据该乘客在该线路下游站点中多天下车量确定，低频乘客下车站点根据所有乘客在该线路下游站点当天下客量确定。

STEP 04：将24小时按照15分钟一个时间片(共96个时间片)进行聚类，对每个时间片内的各条线路上客量、下客量、换乘量进行统计分析。

3.4. 运行结果

本文通过上述方法进行OD识别，以扬州城市对比同类规模城市，算法效率上有较大的优势：扬州有273条线路，1个月数据需要算4.7小时；南昌有752条线路，1个月数据需要算1周。两者效率差约13倍。

4. 公交短时客流预测算法

本文采用间接法SARIMA-RF/XGBoost方法与CNN-LSTM (或LSTM-CNN)方法，和直接法Tensor-ARIMA (融合张量分解与差分自回归滑动平均法)方法进行公交短时客流预测，如图2所示。

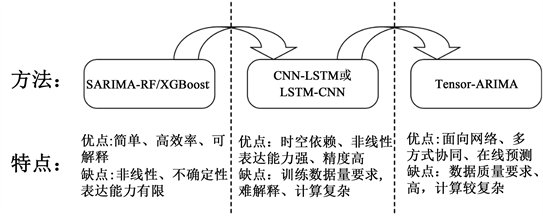
Figure 2. Different methods for short-term passenger flow prediction

图2. 客流短时预测不同方法

4.1. SARIMA-RF/XGBoost方法

基于SARIMA-RF/XGBoost的公交客流OD短时预测基本思想是首先利用SARIMA-RF/XGBoost模型对各站点的上/下客流进行预测，然后以历史公交OD作为种子OD，利用交通分布模型对未来时间段内的OD进行预测。模型结构如下图3所示。

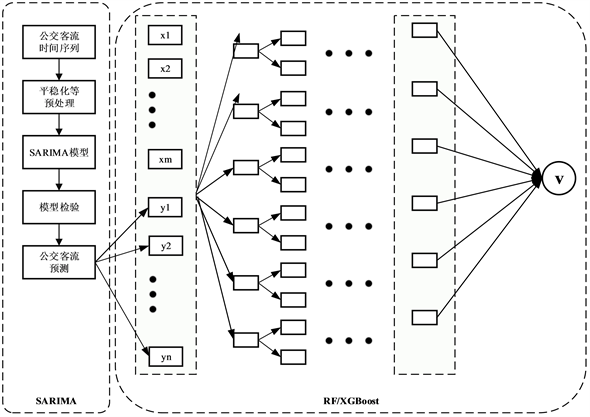
Figure 3. The combined model structure diagram

图3. 组合模型结构图

首先构建季节性差分自回归滑动平均模型SARIMA，利用历史公交客流时间序列数据对未来n个时间段内的客流进行预测，获得 $y_1,y_2,\cdots ,y_n$ ；其次提取历史客流、用地业态、天气、接驳设施等客流影响特征，并与 $y_1,y_2,\cdots ,y_n$ 融合作为随机森林RF与梯度提升机XGBoost的输入特征；然后构建并训练随机森林RF或者梯度提升机XGBoost模型；最后利用训练得到的SARIMA-RF/XGBoost模型对下一时刻客流量进行预测，得到V(T + Δt)。

在各公交站点上客量已知的前提下，采用分布模型中常用的增长率法估算站间OD。增长率法的基本原理就是在现状年出行分布矩阵的基础上，乘以相应的增长函数，得到规划年的出行分布矩阵。

4.2. CNN-LSTM或LSTM-CNN方法

基于深度学习的公交客流OD短时预测首先利用LSTM-CNN或CNN-LSTM深度学习模型对各站点的上/下客流进行预测，然后以历史公交OD作为种子OD，利用交通分布模型对未来时间段内的OD进行预测。模型结构如图4所示。

LSTM-CNN深度学习组合模型如图4(a)所示。LSTM-CNN模型由一个初始LSTM层构成，它将接收公交站点上/下客流序列数据中每一个时间段内的上/下客流作为输入。然后，将LSTM层的输出输入到可以提取局部特征的卷积层中，提取空间依赖特征。最后，卷积层的输出通过池化将被汇集到一个较小的纬度，并串联为特征向量输入至全连接层。通过对全连接层进行dropout等操作后，向后逐层学习输入的抽象特征，以此用于预测站点的上/下客流。

CNN-LSTM深度学习组合模型如图4(b)所示。与LSTM-CNN模型不同，CNN-LSTM 模型的初始层由卷积层构成，以网络中不同站点在各个历史时间段内的上/下客流作为输入，提取各站点之间的空间相关特征。然后，将卷积层的输出通过池化运算汇集到一个较小的尺寸，通过dropout等操作后，联接成为向量输入至LSTM层，通过LSTM循环组件提取历史上不同时间段内上/下客流的时间相关特征。最后，将LSTM的输出作为全连接层的输入向量，向后逐层学习模型输入的抽象特征表达，并基于该特征表达对公交站点未来时间段内的上/下客流进行预测。

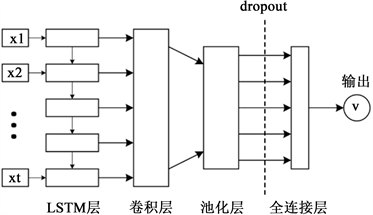(a) (b)

Figure 4. Deep learning model for OD prediction of bus passenger flow

图4. 公交客流OD短时预测深度学习模型

后续仍用交通分布模型中的增长率法进行公交OD短时预测。

4.3. Tensor-ARIMA方法

基于Tensor-ARIMA的公交客流OD短时预测直接面向客流OD矩阵，以历史时间段内的客流OD矩阵数据作为输入，通过结合张量构建、张量分解、ARIMA序列预测、张量重构等步骤，直接对未来时间段内的公交客流OD进行预测，如图5所示。

Figure 5. Short-time prediction of OD of bus passenger flow based on Tensor-ARIMA

图5. 基于Tensor-ARIMA的公交客流OD短时预测

基于Tensor-ARIMA的公交客流OD短时预测模型算法流程可以大致划分为以下步骤：

输入：T个历史时间段内的OD矩阵T(h)；

输出：T + n时间段内的OD矩阵T(f)；

STEP 01：模型建立。基于历史OD数据，通过数据预处理，构建当前时间段OD张量T(h)。

STEP 02：参数标定。利用CP或者Tucker方法对OD张量进行分解，得到因子矩阵。

STEP 03：因子预测。利用ARIMA等时间序列预测方法对时间因子矩阵进行预测，获得未来时间段内的时间因子矩阵。

STEP 04：OD预测。利用CP或者Tucker方法对OD张量进行重构，得到未来时间段内的OD预测值T(f)。

4.4. 运行结果

根据上述三类五种模型，本文对其精度和效率进行计算，其中精度由平均绝对百分比误差和均方误差表示，效率由训练时间和预测时间表示。运算结果如下表2所示。

Table 2. Operation results of three kinds of five models

表2. 三类五种模型运算结果

从上表可以得出，从平均绝对百分比误差和均方误差来看，Tensor + ARIMA的精度较好，SARIMA + XGBoost其次。从训练时间和预测时间来看，Tensor + ARIMA的效率最快，LSTM + CNN和CNN + LSTM其次。

5. 结论

本文对公交OD识别和短时客流预测算法进行了优化设计，以扬州市公交数据对模型进行精度校核和有效性验证。运行结果表明：通过优化算法进行OD识别，以扬州城市对比同类规模城市，算法效率上有较大的优势；五种短时客流预测算法中Tensor + ARIMA在精度和效率上表现最佳。

基金项目

基于GPS和IC卡数据的公交出行OD识别技术研究(HS2022000100)，宁波市交通运输科技项目(202214)，国家自然科学基金(52272334)。