1. 引言
沥青路面是一种路用性能优异并被广泛应用的高级路面类型,随着我国经济的发展,提高沥青路面耐久性和使用寿命已成为中国道路领域的重要任务 [1] 。不同国家沥青路面结构的材料组成、设计标准及控制指标各有不同 [2] ,因此耐久性沥青路面典型结构各具特色。国内学者开展了各类耐久性、长寿命沥青路面结构力学性能的研究 [3] [4] [5] [6] ,交通运输部公路科学研究院的足尺试验环道与同济大学刘力源等人对大厚度、长寿命沥青路面结构进行了研究,取得了一定的研究成果,但整体上并未提出国内外公认的、统一的长寿命或耐久性沥青路面结构组成。研究普遍认为,大粒径沥青混凝土柔性基层是实现耐久性或长寿命沥青路面结构性价比高的解决途径之一 [7] 。本研究基于广西大厚度柔性路面工程应用技术研究项目,以田新高速试验段、主路面结构为原型,开展了大厚度柔性基层沥青路面结构的力学行为随轴载变化的规律研究,研究成果可为大厚度柔性基层沥青路面结构的应用推广提供重要参考。
2. 大厚度柔性路面结构
结合田新高速项目路面结构 [8] 和广西大厚度柔性路面结构的特点,确定的广西大厚度柔性路面结构的试验路段结构如表1所示。

Table 1. Structure and parameters of large-thickness flexible pavement test section
表1. 大厚度柔性路面试验段结构及参数
3. 路面结构Mpave分析模型
 (a) (b)
(a) (b) 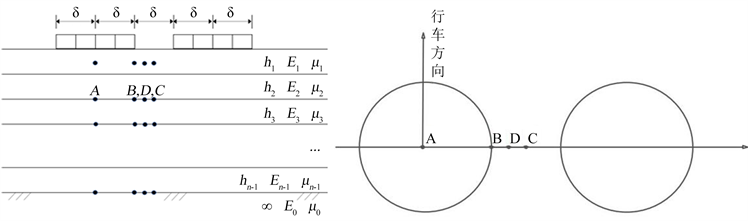 (c) (d)
(c) (d)
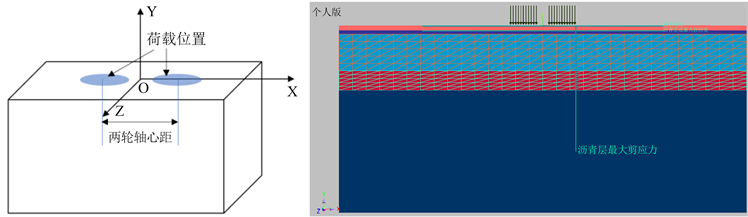
Figure 1. Mechanical calculation model and distribution diagram of load points: (a) Calculation model 3D diagram and coordinate axis; (b) Calculation model discrete grid diagram; (c) Mechanical response calculation point position diagram; (d) Mechanical response calculation load and direction diagram
图1. 力学计算模型及荷载点位分布图:(a) 计算模型三维示意图以及坐标轴;(b) 计算模型离散网格图;(c) 力学响应计算点位置图示;(d) 力学响应计算荷载及方向图示
本研究采用麦路(Mpave)进行力学分析与模拟计算,图1给出了Mpave软件设计与计算用的模型。计算用的标准轴载为0.7 MPa,双圆荷载半径为0.1065 m,两轮中心距为0.3195 m,层间完全连续。坐标原点在双圆荷载的中心点,坐标轴X轴、Y轴与Z轴分别对应着路面模型的垂直行车方向、竖直方向、沿行车方向。其中,A/B/C/D四点分为对应单圆荷载圆心点、单圆圆周点、双圆中心点、单圆圆周点与双圆中心点的中分点 [9] 。
4. 计算分析条件
4.1. 气候、气象条件
广西田新高速项目区1月平均气温为13.8℃,7月平均气温为28.1℃,年平均气温为20.8℃~22.4℃,年无霜期长达340多天,年降雨量1200毫米以上。
4.2. 交通参数
根据广西田新高速项目工可报告资料,本项目车型比例值及交通量预测结果分别见表2。路面设计所采用的交通量数据是根据工程可行性研究报告中“交通量分析与预测”作为设计计算依据。

Table 2. Table of traffic parameters
表2. 交通参数表
4.3. 荷载参数
分别施加0.5 MPa、0.7 MPa、0.9 MPa、1.1 MPa、1.3 MPa等五个双圆均布荷载进行建模,分析力学参数随轴载的变化规律。
5. 力学响应计算结果与分析
5.1. 竖向位移响应规律
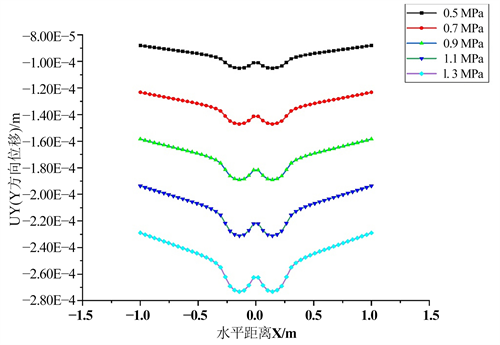
图2给出了大厚度柔性路面结构路表竖向位移UY (沿X轴)随轴载变化的分布图及规律图。图上负值表示为反向位移,正值表示为正向位移,并拟合出了轴载与各计算点位路表竖向位移UY关系式,见表3。可见,随轴载的增加,路表处四个关键计算点位的路表竖向位移UY呈线性增加,增速由大到小为A > B > D > C。
 (a)
(a) (b)
(b)
Figure 2. Change law diagram of vertical displacement of the road surface (along the X-axis): (a) UY distribution diagram (along the X-axis); (b) UY law diagram of key points
图2. 路表竖向位移变化规律图(沿X轴):(a) UY分布图(沿X轴);(b) 关键点位UY规律图

Table 3. UY relation between axle load and vertical displacement of road surface (along the X-axis)
表3. 轴载与路表竖向位移UY关系式(沿X轴)
图3给出了不同轴载下大厚度柔性路面结构沿双圆中心点深度路径的竖向位移UY (沿Y轴)分布图及各层顶的竖向位移变化规律图。图上负值表示为反向位移,正值表示为正向位移,并拟合出了轴载与各层顶竖向位移UY关系式,见表4。可见,随深度的增加,各层顶竖向位移UY均呈减小趋势;随轴载的增加,各层顶竖向位移UY均呈线性关系增加,整体上增速差异不大。
 (a)
(a)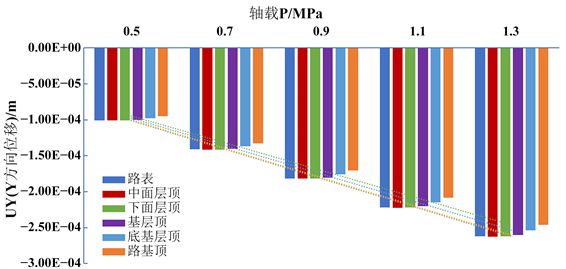 (b)
(b)
Figure 3. UY law diagram of vertical displacement under different axle load (along the Y-axis): (a) UY distribution diagram (along the Y-axis); (b) UY law diagram of each layer top
图3. 不同轴载下深度竖向位移UY规律图(沿Y轴):(a) UY分布图(沿Y轴);(b) 各层顶UY规律图

Table 4. UY relation between axle load and vertical displacement of each layer top (along the Y-axis)
表4. 轴载与各层顶竖向位移UY关系式(沿Y轴)
5.2. 水平拉应力响应规律
 (a)
(a)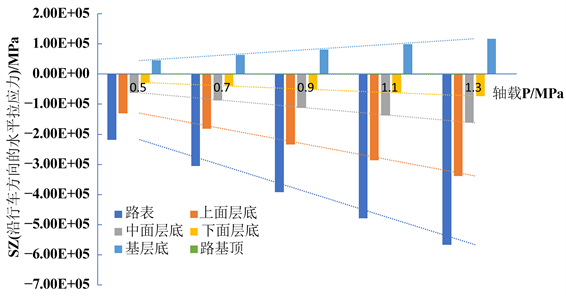 (b)
(b)
Figure 4. SZ law diagram of horizontal tensile stress in running direction under different axle loads (along the Y-axis): (a) SZ distribution diagram (along the Y axis); (b) SZ law diagram of each layer
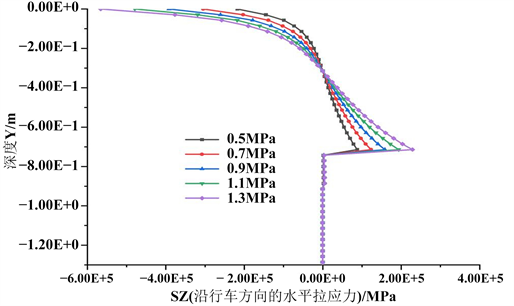
图4. 不同轴载下行车方向水平拉应力SZ规律图(沿Y轴):(a) SZ分布图(沿Y轴);(b) 各层SZ规律图
图4给出了大厚度结构路面结构不同轴载下沿深度X向水平拉应力(沿Y轴)的分布图及规律图。图上负值为压应力,正值为拉应力。具体分析如下:
由分布图可知,路表处行车方向压应力最大,随深度的增加压应力减小,约在下面层附近变为拉应力,至基层底得到一个较大的拉应力;在基层范围内,沿行车方向拉应力随着深度的增加逐渐增大。在底基层内的拉应力随深度的增加变化不大,且拉应力值较小;地基内沿行车方向压应力基本为0。随着轴载的增加,深度沿行车方向水平拉应力的整体变化规律一致。
轴载与各层顶行车方向拉应力SZ (沿Y轴)关系式(沿Y轴)见表5,可见各层顶行车方向拉应力SZ (沿Y轴)均随轴载的增加呈线性关系增加,其中路表增速最大,路基顶基本为0;底基层顶为正增加,其它层顶为负增加;压应力增速由大到小顺序为:路表 > 中面层顶 > 下面层顶 > 基层顶 > 路基顶。

Table 5. SZ relation between axle load and horizontal tensile stress in running direction of each layer top (along the Y axis)
表5. 轴载与各层顶行车方向水平拉应力SZ关系式(沿Y轴)
5.3. 竖向压应变响应规律
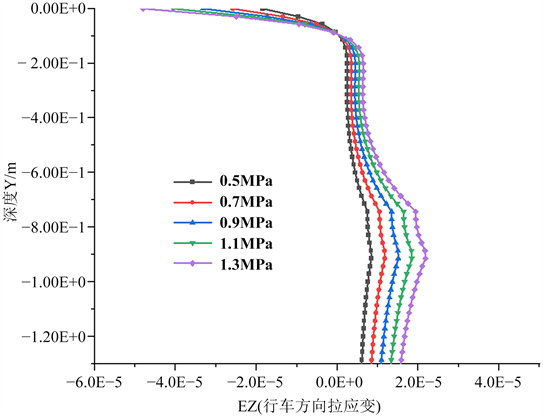
图5给出了不同轴载下大厚度柔性路面结构沿深度方向,沿行车方向的水平拉应变EZ (沿Y轴)的分布图及规律图。图上负值为压应变,正值为拉应变。具体分析如下:
由分布图可知,路表处行车方向压应变最大,随深度的增加压应变减小,应变由压变拉;基层、底基层、路基结构层内拉应变随深度的增加分三段变化:由于双轮荷载的相互作用影响,行车方向拉应变在基层至底基层内随着深度的增加而逐渐增大;在路基中双轮荷载相互作用减弱,行车方向拉应变随路基深度的增加而逐渐减小。随着轴载的增加,沿深度、沿行车方向水平拉应变的整体变化规律一致。
轴载与各层顶行车方向拉应变EZ (沿Y轴)关系式(沿Y轴)见表6,可见各层顶行车方向拉应变EZ (沿Y轴)均随轴载的增加呈线性关系增加,其中路表增速最大,下面层顶增速最小;路表、中面层顶为压应变、负增加,其它层顶为拉应变、正增加;拉应变增速由大到小顺序为:路基顶 > 底基层顶 > 基层顶 > 下面层顶;压应变增速由大到小顺序为:路表 > 中面层顶。
 (a)
(a)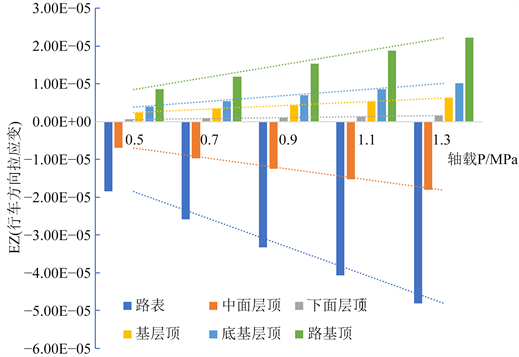 (b)
(b)
Figure 5. Tensile strain law diagram of running direction under different axle loads (along the Y-axis): (a) EZ distribution diagram (along the Y axis); (b) EZ law diagram of each layer
图5. 不同轴载下行车方向拉应变规律图(沿Y轴):(a) EZ分布图(沿Y轴);(b) 各层EZ规律图

Table 6. EZ relation between axle load and tensile strain in running direction of each layer top (along the Y-axis)
表6. 轴载与各层顶行车方向拉应变EZ关系式(沿Y轴)
5.4. 车辙变化规律

Figure 6. Change law of ruts of asphalt layer with axle load
图6. 沥青层车辙随轴载变化规律
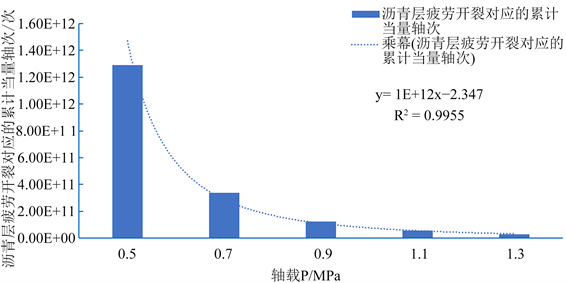
Figure 7. Change law of fatigue life of asphalt layer with axle load
图7. 沥青层疲劳寿命随轴载变化规律
由图6可知,大厚度柔性路面结构的路面车辙深度随轴载的增加呈线性增加,其增长率为8.585。我国现行规范中容许车辙深度设计值为小于15 mm,可见所选的大厚度柔性路面结构的车辙深度在标准轴载0.7 MPa时为13.7 mm,满足设计要求,当轴载超过0.9 MPa后,车辙深度不再满足设计要求。
5.5. 疲劳寿命变化规律
由图7可知,大厚度柔性路面结构的沥青层疲劳寿命随轴载的增加呈指数减少,随轴载增加的降幅非常大。当验算沥青混合料层疲劳开裂时,田新高速公路主线半刚性基层沥青路面设计使用年限内设计车道上的当量设计轴载累计作用次数为4.80E+07,所选大厚度柔性路面结构在1.3 MPa、0.7 MPa、0.5 MPa时的沥青层疲劳开裂对应的累计当量轴载次数分别为2.91E+10,3.40E+11,1.29E+12,可见远远高于常规沥青路面结构的沥青层疲劳寿命。
6. 结论
本文以广西田新高速项目的设计参数和交通条件为基础,提出广西大厚度柔性路面试验段结构,利用离散元软件分析了试验段结构的力学响应随5种不同双圆均布荷载的变化规律,获得如下结论:
1) 随着深度的增加,各层顶竖向位移值慢慢减小;随轴载的增加,不同深度处各层顶竖向位移均呈线性增加,整体上增速差异不大。
2) 路表处行车方向压应力最大,随深度的增加而减小;在下面层附近变为拉应力,至基层底拉应力增加较大;底基层内拉应力随深度的增加变化不大且值较小。各层顶沿行车方向水平拉应力均随轴载的增加呈线性关系增加。
3) 路表处行车方向压应变最大,随深度的增加压应变减小,应变由压变拉;拉应变随基层、底基层深度的增加而增大,随路基深度的增加而减小。
4) 大厚度柔性路面结构的沥青层疲劳寿命随轴载的增加呈指数减少,降幅非常大。对于大厚度柔性路面结构,沥青层疲劳开裂对应的累计当量轴载次数即使在超载下也远高于常规沥青路面结构的沥青层疲劳寿命,寿命长。
基金项目
广西交通运输行业重点科技创新研发项目(桂交便函(2022) 174号No. 8);广西交通投资集团科研项目(田新合工2021-003号);湖南省自然科学基金面上项目(2022JJ30259)。
NOTES
*第一作者。