热光近场空间相干性的多视图立体成像及三维重建方法

Multi View Stereo Imaging Mechanism and Three-Dimensional Reconstruction Method of Thermo Optical near Field Spatial Coherence

摘要: 立体视觉是根据人双眼、昆虫复眼深度视觉原理，通过多个摄像机从不同角度同时获得周围景物的多幅数字图像，由立体匹配技术得到多幅图像上对应点，并且由对应点的视差信息重建三维物体图像。通过热光的近场高阶空间相干性，研究了多视图视觉立体成像，给出了双视图和多视图立体视觉的三维重建公式。

Abstract: Stereo vision is based on the principles of deep vision of human eyes and insect compound eyes. Multiple cameras are used to simultaneously obtain multiple digital images of the surrounding scenery from different angles. Corresponding points on multiple images are obtained through stereo matching technology, and the three-dimensional object image is reconstructed from the disparity information of the corresponding points. Through the near-field high-order spatial coherence of thermal light, the stereo imaging of multi view vision is studied, the three dimensional reconstruction formulas for dual view and multi view stereo vision are provided.

1. 引言

多视图立体视觉的基本原理是从两个以上不同地点观看同一景物 [1] [2] [3] [4] ，获得在不同视角下的多幅感知图像，然后通过三维重建方法和立体匹配原理计算多幅图像像素间对应点的位置视差来重建景物的立体图形，这一过程与人类双眼视觉和昆虫复眼视觉的立体感知过程类似。三维重建方法有射影重建、仿射重建和欧氏几何重建等方法。双眼视差有以视网膜为中心的双眼视差、以头部为中心的双眼视差和两个物体间的相对视差。

射影重建有基于基础矩阵的重建、基于双代数的重建和基于三线约束关系的重建，Faugeras将基础矩阵用于射影重建，Hartley等人对Faugeras的重建方法做了一些改进和发展。Rota等学者对19世纪的双代数射影几何重建给出改进，Carlsson推导了一些双代数形式的不变量表达式，Shashua利用几何不变量理论得到3幅二维图像间对应匹配点坐标的三线约束关系。

仿射重建有基于模约束的重建和基于摄像机平移运动的重建，Luong等学者将模约束的概念来进行摄像机自标定，Peter Sterm利用图像中的灭点及模约束来实现物体的仿射重建，当摄像机在两幅图像间平移运动时，两幅图像间的仿射变换可实现物体的三维重建。

在欧氏几何下，三维重建的一般方法是在左右摄像机内外参数已知时，计算出空间直线重组三维面、二次曲面，然后重建出三维物体立体图像。当左摄像机坐标系和右摄像机坐标系平行时，可以通过立体成像几何法得到三维重建公式。一般情形下二维成像图像和三维场景之间存在着投影关系，这种投影关系是摄像机的投影矩阵，可以通过左右两幅图像上少量的对应点信息来恢复投影矩阵，由左右双摄像机投影矩阵，利用最小二乘法得到精度比较高的图像上每一点的深度信息，从而重建物体的三维图像。

复眼多目视觉由多视图几何的多视图张量 [5] ，产生多幅图像测量坐标的多重线性关系，每幅图像的摄像机矩阵从张量计算得到，三维立体图像可以由恢复的摄像机和多幅图像上的对应点视差计算得到。

人类立体视觉系统通过双眼视差感知三维信息，文献 [6] [7] [8] 中描述了双眼视差的基本原理和类型。如图1所示，以视网膜为中心的双眼视差是物体A为 ${\alpha }_L-{\alpha }_R$ ，物体B为 ${\beta }_L-{\beta }_R$ ，以头部为中心的双眼视差是物体A为 $\left({\alpha }_L+{\gamma }_L\right)-\left({\alpha }_R+{\gamma }_R\right)$ ，物体B为 $\left({\beta }_L+{\gamma }_L\right)-\left({\beta }_R+{\gamma }_R\right)$ ，物体A、B的双眼相对视差都是 $\left({\alpha }_L-{\alpha }_R\right)-\left({\beta }_L-{\beta }_R\right)$ 。

Figure 1. Retinal disparity and head centered disparity map

图1. 视网膜视差和以头为中心的视差图

Figure 2. HBT interferometer

图2. HBT干涉仪

人双眼的立体匹配在观看场景物体的同时自然发生的，但双目视觉与人双眼不同，需要经过专门的立体匹配方法才能得到左右两幅图像上的对应点。目前为止还没有学者运用量子光学的热光近场二阶相干性来研究双眼立体视觉的感知机制。

文献 [9] [10] [11] 详细介绍了热光近场的一阶相干性、二阶相干性、高阶相干性和量子成像原理，热光的近场的二阶相干函数 ${\Gamma }^{\left(2\right)}\left(q_1,t_1;q_2,t_2\right)$ 是由两个光探测器分别在时空点 $\left(q_1,t_1\right)$ 和 $\left(q_2,t_2\right)$ 的光场 $E\left(q_j,t_j\right)$ 作直接符合测量，如图2所示的HBT干涉仪 [9] ，由放在小孔后面的两台独立光探测器对发生在时空点 $\left(q_1,t_1\right)$ 和 $\left(q_2,t_2\right)$ 处的两个不同的事件做联合观测，图2中的观测是基于电学的线性乘法器处的联合电流：

$i_1\left(t\right)i_2\left(t\right)\propto I_1\left(q_1,t_1\right)I_2\left(q_2,t_2\right)=E^{*}\left(q_1,t_1\right)E\left(q_1,t_1\right)E^{*}\left(q_2,t_2\right)E\left(q_2,t_2\right)$ 。

二阶相干函数 ${\Gamma }^{\left(2\right)}$ 与一阶相干函数 ${\Gamma }_{11}^{\left(1\right)}$ 、 ${\Gamma }_{22}^{\left(1\right)}$ 和 ${\Gamma }_{12}^{\left(1\right)}$ 有关： ${\Gamma }^{\left(2\right)}={\Gamma }_{11}^{\left(1\right)}{\Gamma }_{22}^{\left(1\right)}+{\Gamma }_{12}^{\left(1\right)}$ 。N阶相干函数是：

${\Gamma }^{\left(N\right)}\left(q_1,z_1;\cdots ;q_N,z_N\right)=\langle E^{*}\left(q_1,z_1\right)E\left(q_1,z_1\right)E^{*}\left(q_2,z_2\right)E\left(q_2,z_2\right)\cdots E^{*}\left(q_N,z_N\right)E\left(q_N,z_N\right)\rangle$ 。

设 $O_l\left(x_l,y_l,z_l\right)$ 是左摄像机坐标系， $O_r\left(x_r,y_r,z_r\right)$ 是右摄像机坐标系， $O_w\left(x_w,y_w,z_w\right)$ 是世界坐标系， $P_l$ 、 $P_r$ 和 $P_w$ 分别是三个坐标系 $O_l$ 、 $O_r$ 和 $O_w$ 中的点。通过图像特征点匹配、对极几何恢复、稀疏匹配和稠密匹配、局部匹配和全局匹配等立体匹配方法，找到左边图像和右边图像上的对应点 $q_{wl}$ 和 $q_{wr}$ 。

本文将两个独立的联合二阶相干测量变成双目成像系统的联合符合测量，则二阶相干函数 ${\Gamma }^{\left(2\right)}$ 测量的结果就是双目视觉的立体成像，得到的主要结果是：

1) 根据三角测量原理得到双目视图立体视觉成像的三维重建公式：

$P_w=\frac{1}{m}\frac{q_{wl}+q_{wr}}{2}+\left(1-\frac{1}{m}\right)\frac{t_{wl}+t_{wr}}{2}.$ (1)

其中 $m_l=m_r=m=\frac{\left|q_{wl}-q_{wr}-\left(t_{wl}-t_{wr}\right)\right|}{\left|t_{wl}-t_{wr}\right|}$ 或者 $m=1\pm \frac{\left|q_{wl}-q_{wr}\right|}{\left|t_{wl}-t_{wr}\right|}$ 是摄像机成像系统的放大率， $t_{wl}$ 、 $t_{wr}$ 分别是左右摄像机在世界坐标系中的平移位置向量， $q_{wl}-q_{wr}$ 是以视网膜为中心的双眼视差， $\left(q_{wl}-t_{wl}\right)-\left(q_{wr}-t_{wr}\right)$ 是以头部为中心的双眼视差。

2) 设 $\left|V\right|$ 个摄像机分别位于连通图 $G=G\left(V,E\right)$ 的节点上，其中V、E分别是G的节点集、边集， $q_{wu}$ 是第 $u\left(u\in V\right)$ 幅图像上的成像点，则多目视图立体视觉成像的三维重建公式为：

$P_w=\frac{1}{\left|E\right|}{\displaystyle \underset{\left(u,v\right)\in E}{\sum }\left(\frac{q_{wu}+q_{wv}}{m_u+m_v}+\frac{\left(m_u-1\right)t_{wu}+\left(m_u-1\right)t_{wv}}{m_u+m_v}\right)}.$ (2)

其中 $t_{wu}$ 是第u个摄像机在世界坐标系中的平移位置向量， $m_u$ 是第u个摄像机的放大率。

3) 根据热光的近场二阶空间相干性得到双视图立体成像的三维重建公式：

${\Gamma }_{lr}^{\left(1\right)}\left(q_{wl};q_{wr}\right)\propto {\left|{\text{e}}^{i\frac{\omega }{2c{s}_i}\left({\left|q_{wl}\right|}^2-{\left|q_{wr}\right|}^2\right)}{\displaystyle {\int }_{obj}\text{d}{q}_o}{A}^2\left(q_o\right)somb\left(\frac{R}{s_o}\frac{\omega }{c}\left|q_o+\frac{q_{wl}+q_{wr}}{2m}\right|\right)somb\left(\frac{R}{s_i}\frac{\omega }{c}\left|q_{wl}-q_{wr}\right|\right)\right|}^2.$ (3)

其中 $somb\left(x\right)=\frac{2J_1\left(x\right)}{x}$ ， $J_1\left(x\right)$ 是一阶贝赛尔函数， $s_o$ 是物体和成像透镜间的距离， $s_i$ 是成像透镜和像平面间的距离，R是成像透镜半径， $A\left(q_o\right)$ 是物体光场的分布函数， $m=\frac{s_i}{s_o}$ 是成像系统的放大率， $\left|q_{wl}-q_{wr}\right|$ 为双眼视差。

4) 设 $\left|V\right|$ 个光探测器分别位于连通图 $G=G\left(V,E\right)$ 的节点上，其中V、E分别是G的节点集、边集， $U\subset V$ ， $G_U=G\left(V-U,E_U\right)$ 是节点集为 $V-U$ 的G的子图，子图 $G_U$ 中没有孤立节点，若 $G_U$ 有孤立节点，则将这个节点加入到U中，重新得到的子图就没有孤立节点。假设 $\left|V\right|$ 个成像系统的各个参数都相同，任意的节点 $u,v\in V$ ， $s_{ou}=s_{ov}=s_o$ ， $s_{iu}=s_{iv}=s_i$ ， $m_u=m_v=m$ ， $f_u=f_v=f$ ， $z_u=z_v=d$ 。根据热光的近场 $\left|V\right|$ 阶空间相干性得多视图立体成像的三维重建公式：

$\begin{array}{l}{\Gamma }^{\left(\left|V\right|\right)}\left(q_{w1},\cdots ,q_{w\left|V\right|}\right)\propto {\displaystyle \underset{U\subset V}{\sum }{\displaystyle \underset{\left(u,v\right)\in E_U}{\prod }(|{\text{e}}^{i\frac{\omega }{2c{s}_i}\left({\left|q_{wu}\right|}^2-{\left|q_{wv}\right|}^2\right)}}}{\displaystyle {\int }_{obj}\text{d}{q}_o}{A}^2\left(q_o\right)somb\left(\frac{R}{s_o}\frac{\omega }{c}\left|q_o+\frac{q_{wu}+q_{wv}}{2m}\right|\right)\\ \times somb{\left(\frac{R}{s_i}\frac{\omega }{c}\left|q_{wu}-q_{wv}\right|\right)|}^2).\end{array}$ (4)

文中给出的三维重建公式(1)、(2)中有摄像机的放大率、平移向量和两幅图像和多幅图像上的对应点信息，不需要摄像机旋转参数信息，所得到三维重建公式计算量比现有的文献中的三维重建公式都少。由热光近场的高阶空间相干性得到多视图成像的三维重建公式(3)和公式(4)，在进行多个光探测器符合立体测量成像时就自动完成了多幅图像上的对应点立体匹配，并且证明和验证了三角测量原理和高斯透镜公式的正确性，而现有的文献中的三维重建公式需要有多幅图像上的对应点匹配信息，计算量就比较大。

2. 双目视觉及多目视觉成像的三维重建公式

三角形测量原理如图3所示 [2] ，摄像机坐标系是 $\left(x_c,y_c,z_c\right)$ ，成像平面是 $z_c=f_c$ 。设 $q_c={\left(u,v,w\right)}^{\text{T}}$ 是图像平面上任一点， $P_c={\left(x_c,y_c,z_c\right)}^{\text{T}}$ 是空间中的任一点，由三角形相似原理有：

$u=\frac{x_c}{z_c}{f}_c,v=\frac{y_c}{z_c}{f}_c,w=f_c,q_c=\frac{f_c}{z_c}{p}_c.$

设 $m_c=\frac{f_c}{z_c}$ ， $m_c$ 是成像放大率，则有：

$\left(u,v,w\right)=\left(\frac{x_c}{z_c}{f}_c,\frac{y_c}{z_c}{f}_c,f_c\right)=\frac{f_c}{z_c}\left(x_c,y_c,z_c\right),q_c=m_c{P}_c.$ (5)

Figure 3. Triangle measurement

图3. 三角形测量原理图

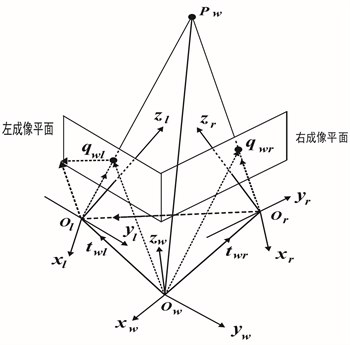
Figure 4. Geometric schematic diagram of principle diagram converging optical axis binocular imaging

图4. 汇聚式光轴双目成像几何原理图

双目汇聚式光轴立体成像几何原理如图4所示，三个坐标系 $O_l\left(x_l,y_l,z_l\right)$ 、 $O_r\left(x_r,y_r,z_r\right)$ 、 $O_w\left(x_w,y_w,z_w\right)$ 之间的坐标变换是：

$P_l=R_l{P}_w+t_{lw}=R_l\left(P_w-t_{wl}\right),P_r=R_r{P}_w+t_{rw}=R_r\left(P_w-t_{wr}\right).$ (6)

其中 $R_l$ 、 $R_r$ 是坐标系之间的旋转矩阵。

由公式(5)和(6)得： $q_l=m_l{P}_l$ ， $q_r=m_r{P}_r$ ， $q_l=R_l\left(q_{wl}-t_{wl}\right)$ ， $q_r=R_r\left(q_{wr}-t_{wr}\right)$ ，所以有： $R_l\left(q_{wl}-t_{wl}\right)=m_l{R}_l\left(P_w-t_{wl}\right)$ ， $R_r\left(q_{wr}-t_{wr}\right)=m_r{R}_r\left(P_w-t_{wr}\right)$ 。

$R_l$ 和 $R_r$ 都是可逆矩阵，于是有 $q_{wl}-t_{wl}=m_l\left(P_w-t_{wl}\right),q_{wr}-t_{wr}=m_r\left(P_w-t_{wr}\right)$ ，解得：

$P_w=\frac{q_{wl}+q_{wr}}{m_l+m_r}+\frac{\left(m_l-1\right)t_{wl}+\left(m_r-1\right)t_{wr}}{m_l+m_r}.$ (7)

$\frac{q_{wl}+\left(m_l-1\right)t_{wl}}{m_l}=\frac{q_{wr}+\left(m_r-1\right)t_{wr}}{m_r}.$ (8)

由(8)式得： $\frac{q_{wl}-t_{wl}}{m_l}-\frac{q_{wr}-t_{wr}}{m_r}=t_{wr}-t_{wl}$ 或 $\frac{q_{wl}}{m_l}-\frac{q_{wr}}{m_r}=\left(\frac{1}{m_l}-1\right)t_{wl}-\left(\frac{1}{m_r}-1\right)t_{wr}$ 。

当左右摄像机的放大率 $m_l=m_r=m$ 时，由(7)式和上式得： $P_w=\frac{1}{2m}\left(q_{wl}+q_{wr}\right)+\frac{m-1}{2m}\left(t_{wl}+t_{wr}\right)$ ，于是得到公式(1)，并且有：

$m\left(t_{wr}-t_{wl}\right)=q_{wl}-q_{wr}-\left(t_{wl}-t_{wr}\right)$ ，或者 $\left(1-m\right)\left(t_{wl}-t_{wr}\right)=q_{wl}-q_{wr}$ 。

这两个等式两边取向量的长度得：

$m=\frac{\left|q_{wl}-t_{wl}-\left(q_{wr}-t_{wr}\right)\right|}{\left|t_{wl}-t_{wr}\right|}$ ，或者 $m=1\pm \frac{\left|q_{wl}-q_{wr}\right|}{\left|t_{wl}-t_{wr}\right|}$ 。

根据双眼视差的定义 [7] 和图1、图4可知， $\left(q_{wl}-t_{wl}\right)-\left(q_{wr}-t_{wr}\right)$ 是以头部为中心的双眼视差， $q_{wl}-q_{wr}$ 是以视网膜为中心的双眼视差。

设 $\left|V\right|$ 个摄像机分别位于连通图 $G=G\left(V,E\right)$ 的节点上，其中V、E分别是G的节点集、边集。对于多目立体视觉，第 $u\left(u\in V\right)$ 个摄像机几何模型是 $q_{wu}-t_{wu}=m_u\left(P_w-t_{wu}\right)$ ，对于任意节点 $u\in V$ ，由于 $q_{wu}-t_{wu}=m_u\left(P_w-t_{wu}\right)$ ，任一边 $\left(u,v\right)\in E$ ，将相邻节点上的摄像机模型

相加得： $q_{wu}+q_{wv}-t_{wu}-t_{wv}=m_u\left(P_w-t_{wu}\right)+m_v\left(P_w-t_{wv}\right)$ ，解得：

$P_{w,\left(u,v\right)}=\frac{q_{wu}+q_{wv}}{m_u+m_v}+\frac{\left(m_u-1\right)t_{wu}+\left(m_u-1\right)t_{wv}}{m_u+m_v}$ ，

并且有： $\frac{q_{wu}-t_{wu}}{m_u}-\frac{q_{wv}-t_{wv}}{m_v}=t_{wv}-t_{wv}$ 。将 $\left|E\right|$ 个 $P_{w,\left(u,v\right)}$ 取平均值得多目立体视觉三维重建公式(2)。

本节得到的三维重建公式是目前为止的文献 [12] - [19] 中没有出现过的，其创新点是公式(1)、(2)、(7)和(8)。

3. 热光的近场高阶空间相干性的三维重建公式

热光近场的经典成像系统如图5所示 [9] ，像平面上的光场是：

$E\left(q_j,z_j,t\right)={\displaystyle \int E}\left(k,\omega ;q_o,z_0=0,t_0=0\right)g\left(k,\omega ;q_j,z_j,t\right)\text{d}\omega \text{d}k.$ (9)

Figure 5. Imaging system diagram

图5. 量子光学的成像系统图

成像系统的格林函数是：

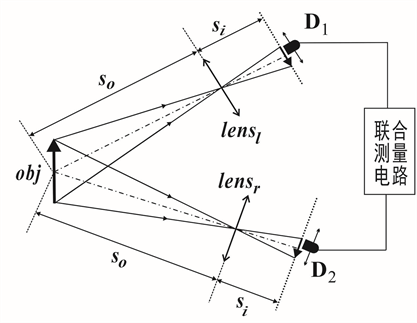
Figure 6. Stereometric measurement of thermal near-of quantum optics field second-order coherence for binocular vision

图6. 双目视觉的热光近场二阶相干性立体测量图

$\begin{array}{l}g\left(k,\omega ;q_j,z=s_o+s_i\right)\\ ={\displaystyle {\int }_{obj}\text{d}{q}_o}{\displaystyle {\int }_{lens}\text{d}{q}_l}\left\{A\left(q_o\right){\text{e}}^{ik·q_o}\right\}\left\{\frac{i\omega }{2\pi c}\frac{{\text{e}}^{i\frac{\omega }{c}{s}_o}}{s_o}G\left(\left|q_l-q_o\right|,\frac{\omega }{c{s}_o}\right)\right\}\left\{G\left(\left|q_l\right|,-\frac{\omega }{cf}\right)\right\}\left\{\frac{i\omega }{2\pi c}\frac{{\text{e}}^{i\frac{\omega }{c}{s}_i}}{s_i}G\left(\left|q_j-q_l\right|,\frac{\omega }{c{s}_i}\right)\right\}\end{array}$

其中 $q_o$ 、 $q_l$ 和 $q_j$ 分别是物平面、透镜平面和像平面上的二维坐标向量， $G\left(\left|\alpha \right|,\beta \right)={\text{e}}^{i\left(\frac{\beta }{2}\right){\left|\alpha \right|}^2}$ 是菲涅耳相位因子(高斯函数)， $s_o$ 是物体和成像透镜间的距离， $s_i$ 是成像透镜和像平面间的距离， $A\left(q_o\right)$ 是物体光场分布函数。

利用高斯函数的性质，上式简化为下述形式：

$\begin{array}{c}g\left(k,\omega ;q_j,z=s_o+s_i\right)=\frac{-{\omega }^2}{{\left(2\pi c\right)}^2{s}_o{s}_i}{\text{e}}^{i\frac{\omega }{c}\left(s_o+s_i\right)}G\left(\left|q_j\right|,\frac{\omega }{c{s}_i}\right){\displaystyle {\int }_{obj}\text{d}{q}_o}A\left(q_o\right)G\left(\left|q_o\right|,\frac{\omega }{c{s}_o}\right){\text{e}}^{ik\cdot q_o}\\ \times {\displaystyle {\int }_{lens}\text{d}{q}_l}G\left[\left|q_l\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_j}{s_i}\right)\cdot q_l}.\end{array}$ (10)

对于半径为R的有限尺寸透镜，上式中的第二个重积分简化得到该成像系统的点扩展函数：

${\displaystyle {\int }_{lens}\text{d}{q}_l}G\left[\left|q_l\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_j}{s_i}\right)\cdot q_l}\propto somb\left(\frac{R}{s_o}\frac{\omega }{c}\left|q_o+\frac{q_j}{m}\right|\right).$ (11)

其中 $somb\left(x\right)=\frac{2J_1\left(x\right)}{x}$ ， $J_1\left(x\right)$ 是一阶贝赛尔函数， $m=\frac{s_i}{s_o}$ 是成像系统的放大率。

热光的近场二阶空间相干函数 [9] 是：

$\begin{array}{c}{\Gamma }^{\left(2\right)}\left(q_1,z_1;q_2,z_2\right)={\displaystyle \underset{j}{\sum }{\displaystyle \underset{l}{\sum }{\left|\frac{1}{\sqrt{2}}\left[E_j\left(q_1,z_1\right)E_l\left(q_2,z_2\right)+E_l\left(q_1,z_1\right)E_j\left(q_2,z_2\right)\right]\right|}^2}}\\ ={\displaystyle \int \text{d}{k}_1\text{d}{k}_2}{\left|\frac{1}{\sqrt{2}}\left[g\left({\stackrel{\to }{q}}_1,z_1,k_1\right)g\left(q_2,z_2,k_2\right)+g\left(q_2,z_2,k_1\right)g\left(q_1,z_1,k_2\right)\right]\right|}^2\\ ={\displaystyle \int \text{d}{k}_1}{\left|g\left(q_1,z_1,k_1\right)\right|}^2{\displaystyle \int \text{d}{k}_2}{\left|g\left(q_2,z_2,k_2\right)\right|}^2+{\left|{\displaystyle \int \text{d}k}{g}^{*}\left(q_1,z_1,k\right)g\left(q_2,z_2,k\right)\right|}^2.\\ ={\Gamma }_{11}^{\left(1\right)}\left(q_1,z_1\right){\Gamma }_{22}^{\left(1\right)}\left(q_2,z_2\right)+{\Gamma }_{12}^{\left(1\right)}\left(q_1,z_1;q_2,z_2\right).\end{array}$ (12)

将自由传播的格林函数 $g\left(q_j,z_j,k\right)=\frac{-\omega }{2\pi c}\frac{{\text{e}}^{i\frac{\omega }{c}{z}_j}}{z_j}{\displaystyle \int \text{d}{q}_o}A\left(q_o\right){\text{e}}^{ik\cdot q_o}{\text{e}}^{i\frac{\omega }{2c{z}_j}{\left|q_j-q_o\right|}^2}$ 代入上式得到一阶空间相干函数 ${\Gamma }_{11}^{\left(1\right)}{\Gamma }_{22}^{\left(1\right)}~$ 常数， ${\Gamma }_{12}^{\left(1\right)}\left(q_1,z_1;q_2,z_2\right)={\displaystyle \int \text{d}k}{g}^{*}\left(q_1,z_1,k\right)g\left(q_2,z_2,k\right)$ 。假设 $A^2\left(q_o\right)~$ 常量， $z_1=z_2=d$ ，则得到： ${\Gamma }_{12}^{\left(1\right)}\left(q_1;q_2\right)\propto {\text{e}}^{-i\frac{\omega }{2cd}\left({\left|q_1\right|}^2-{\left|q_2\right|}^2\right)}{\displaystyle \int \text{d}{q}_o}{A}^2\left(q_o\right){\text{e}}^{i\frac{\omega }{cd}\left(q_1-q_2\right)\cdot q_o}\propto {\text{e}}^{-i\frac{\omega }{2cd}\left({\left|q_1\right|}^2-{\left|q_2\right|}^2\right)}somb\left(\frac{R}{d}\frac{\omega }{c}\left|q_1-q_2\right|\right)$ 。

如图6所示，将HBT干涉仪在在两个独立观测点 $\left(q_{wl},t_l\right)$ 和 $\left(q_{wr},t_r\right)$ 的联合测量变为两个成像系统的联合测量，HBT干涉仪就变成双目视觉的立体成像测量。

左右摄像机成像高斯透镜公式 $\frac{1}{s_{oj}}+\frac{1}{s_{ij}}=\frac{1}{f_j},j\in \left\{l,r\right\}$ ，将成像系统的格林函数(10)式代入到(12)式得：

$\begin{array}{c}{\Gamma }_{lr}^{\left(1\right)}\left(q_{wl},z_l;q_{wr},z_r\right)={\left|{\displaystyle \int \text{d}}k{g}^{*}\left(q_{wl},z_l,k\right)g\left(q_{wr},z_r,k\right)\right|}^2\\ =|\frac{-{\omega }^2}{{\left(2\pi c\right)}^2{s}_{ol}{s}_{il}}{\text{e}}^{-i\frac{\omega }{c}\left(s_{ol}+s_{il}\right)}{G}^{*}\left(\left|q_{wl}\right|,\frac{\omega }{c{s}_{il}}\right){\displaystyle {\int }_{ob{j}_l}\text{d}{q}_{ol}}A\left(q_{ol}\right)G^{*}\left(\left|q_{ol}\right|,\frac{\omega }{c{s}_{ol}}\right){\text{e}}^{-ik\cdot q_{ol}}\\ \times {\displaystyle {\int }_{len{s}_l}\text{d}{q}_{l_l}}{G}^{*}\left[\left|q_{l_l}\right|,\frac{\omega }{c}\left(\frac{1}{s_{ol}}+\frac{1}{s_{il}}-\frac{1}{f_l}\right)\right]{\text{e}}^{i\frac{\omega }{c}\left(\frac{q_{ol}}{s_{ol}}+\frac{q_{wl}}{s_{il}}\right)\cdot q_{l_l}}\\ \times \frac{-{\omega }^2}{{\left(2\pi c\right)}^2{s}_{or}{s}_{ir}}{\text{e}}^{i\frac{\omega }{c}\left(s_{or}+s_{ir}\right)}G\left(\left|q_{wr}\right|,\frac{\omega }{c{s}_{ir}}\right){\displaystyle {\int }_{ob{j}_r}\text{d}{q}_{or}}A\left(q_{or}\right)G\left(\left|q_{or}\right|,\frac{\omega }{c{s}_{or}}\right){\text{e}}^{ik\cdot q_{or}}\\ \times {{\displaystyle {\int }_{len{s}_r}\text{d}{\stackrel{\to }{q}}_{l_r}}G\left[\left|q_{l_r}\right|,\frac{\omega }{c}\left(\frac{1}{s_{or}}+\frac{1}{s_{ir}}-\frac{1}{f_r}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_{or}}{s_{or}}+\frac{q_{wr}}{s_{ir}}\right)\cdot q_{l_r}}|}^2.\end{array}$

设左右成像系统的物体上光场分布相同， $A\left(q_{ol}\right)=A\left(q_{or}\right)=A\left(q_o\right)$ ，则有：

$\begin{array}{c}{\Gamma }_{lr}^{\left(1\right)}\left(q_{wl},z_l;q_{wr},z_r\right)=|\frac{{\omega }^4}{{\left(2\pi c\right)}^4}\frac{1}{s_{ol}{s}_{or}{s}_{il}{s}_{ir}}{\text{e}}^{-i\frac{\omega }{c}\left(z_l-z_r\right)}{G}^{*}\left(\left|q_{wl}\right|,\frac{\omega }{c{s}_{il}}\right)G\left(\left|q_{wr}\right|,\frac{\omega }{c{s}_{ir}}\right)\\ \times {\displaystyle {\int }_{obj}\text{d}{q}_o}{A}^2\left(q_o\right)G^{*}\left(\left|q_o\right|,\frac{\omega }{c{s}_{ol}}\right)G\left(\left|q_o\right|,\frac{\omega }{c{s}_{or}}\right)\\ \times {\displaystyle {\int }_{len{s}_l}\text{d}{q}_{l_l}}{G}^{*}\left[\left|q_{l_l}\right|,\frac{\omega }{c}\left(\frac{1}{s_{ol}}+\frac{1}{s_{il}}-\frac{1}{f_l}\right)\right]{\text{e}}^{i\frac{\omega }{c}\left(\frac{q_o}{s_{ol}}+\frac{q_{wl}}{s_{il}}\right)\cdot q_{l_l}}\\ \times {{\displaystyle {\int }_{len{s}_r}\text{d}{q}_{l_r}}G\left[\left|q_{l_r}\right|,\frac{\omega }{c}\left(\frac{1}{s_{or}}+\frac{1}{s_{ir}}-\frac{1}{f_r}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_{or}}+\frac{q_{wr}}{s_{ir}}\right)\cdot q_{l_r}}|}^2.\end{array}$ (13)

上式进一步再简化，设 $s_{ol}=s_{or}=s_o,s_{il}=s_{ir}=s_i,m_l=m_r=m,f_l=f_r=f$ ，则有：

$\begin{array}{c}{\Gamma }_{lr}^{\left(1\right)}\left(q_{wl};q_{wr}\right)=|\frac{{\omega }^4}{{\left(2\pi c\right)}^4}\frac{1}{s_o^2{s}_i^2}{G}^{*}\left(\left|q_{wl}\right|,\frac{\omega }{c{s}_i}\right)G\left(\left|q_{wr}\right|,\frac{\omega }{c{s}_i}\right){\displaystyle {\int }_{obj}\text{d}{q}_o}{A}^2\left(q_o\right)\\ \times {\displaystyle {\int }_{len{s}_l}\text{d}{q}_{l_l}}{G}^{*}\left[\left|q_{l_l}\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wl}}{s_i}\right)\cdot q_{l_l}}\\ \times {{\displaystyle {\int }_{len{s}_r}\text{d}{q}_{l_r}}G\left[\left|q_{l_r}\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wr}}{s_i}\right)\cdot q_{l_r}}|}^2\\ =|\frac{{\omega }^4}{{\left(2\pi c\right)}^4}\frac{1}{s_o^2{s}_i^2}{\text{e}}^{i\frac{\omega }{2c{s}_i}\left({\left|q_{wr}\right|}^2-{\left|q_{wl}\right|}^2\right)}{\displaystyle {\int }_{obj}\text{d}{q}_o}{A}^2\left(q_o\right)\\ \times {\displaystyle {\int }_{len{s}_l}\text{d}{q}_{l_l}}{G}^{*}\left[\left|q_{l_l}\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wl}}{s_i}\right)\cdot q_{l_l}}\\ \times {{\displaystyle {\int }_{len{s}_r}\text{d}{q}_{l_r}}G\left[\left|q_{l_r}\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wr}}{s_i}\right)\cdot q_{l_r}}|}^2.\end{array}$

由于

$\begin{array}{l}\left(\frac{q_o}{s_o}+\frac{q_{wr}}{s_i}\right)\cdot q_{l_r}-\left(\frac{q_o}{s_o}+\frac{q_{wl}}{s_i}\right)\cdot q_{l_l}=\frac{1}{s_o}\left[q_o\cdot \left(q_{l_r}-q_{l_l}\right)+\frac{q_{wr}}{m}\cdot q_{l_r}-\frac{q_{wl}}{m}\cdot q_{l_l}\right]\\ =\frac{1}{s_o}\left[\left(q_o+\frac{q_{wr}+q_{wl}}{2m}\right)\cdot \left(q_{l_r}-q_{l_l}\right)+\frac{1}{2m}\left(q_{wr}-q_{wl}\right)\cdot \left(q_{l_r}+q_{l_l}\right)\right].\end{array}$

高斯透镜公式成立时有：

$\begin{array}{l}{\displaystyle {\int }_{len{s}_l}\text{d}{q}_{l_l}}{G}^{*}\left[\left|q_{l_l}\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wl}}{s_i}\right)\cdot q_{l_l}}{\displaystyle {\int }_{len{s}_r}\text{d}{q}_{l_r}}G\left[\left|q_{l_r}\right|,\frac{\omega }{c}\left(\frac{1}{s_o}+\frac{1}{s_i}-\frac{1}{f}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wr}}{s_i}\right)\cdot q_{l_r}}\\ ={\displaystyle {\int }_{len{s}_l}\text{d}{q}_{l_l}}{\text{e}}^{i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wl}}{s_i}\right)\cdot q_{l_l}}{\displaystyle {\int }_{len{s}_r}\text{d}{q}_{l_r}}{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_o}+\frac{q_{wr}}{s_i}\right)\cdot q_{l_r}}\\ ={\displaystyle {\int }_{len{s}_l}{\displaystyle {\int }_{len{s}_r}\text{d}}}\left(q_{l_r}-q_{l_l}\right){\text{e}}^{-i\frac{\omega }{c{s}_o}\left(q_o+\frac{q_{wr}+q_{wl}}{2m}\right)\cdot \left(q_{l_r}-q_{l_l}\right)}{\displaystyle {\int }_{len{s}_l}{\displaystyle {\int }_{len{s}_r}\text{d}}}\left(q_{l_r}+q_{l_l}\right){\text{e}}^{-i\frac{\omega }{2cm{s}_o}\left(q_{wr}-q_{wl}\right)\cdot \left(q_{l_r}+q_{l_l}\right)}.\end{array}$

所以得到热光近场一阶相干函数的三维重建公式(3)。

在一阶相干函数 ${\Gamma }_{lr}^{\left(1\right)}$ 式中， $q_0=-P_w$ ，扩展函数 $somb\left(\frac{R}{s_o}\frac{\omega }{c}\left|q_o+\frac{q_{wl}+q_{wr}}{2m}\right|\right)$ 中有世界坐标系中的向量 $P_w$ ，扩展函数 $somb\left(\frac{R}{s_i}\frac{\omega }{c}\left|q_{wl}-q_{wr}\right|\right)$ 包括两幅图像上对应点 $q_{wl}$ 、 $q_{wr}$ 的视差信息。所以由(3)式，对双目视觉的两幅图像进行联合符合测量，重建物体的三维图形，并且扩展函数 $somb\left(\frac{R}{s_i}\frac{\omega }{c}\left|q_{wl}-q_{wr}\right|\right)$ 对左右两幅图像对应点同时进行了实时立体匹配。

设 $\left|V\right|$ 个光探测器分别位于连通图 $G=G\left(V,E\right)$ 的节点上，将HBT干涉仪在 $\left|V\right|$ 个独立观测点 $\left(q_{wu},t_u\right)\left(u\in V\right)$ 联合测量变为 $\left|V\right|$ 个成像系统的联合测量，HBT干涉仪就变成多目视觉的立体成像测量，热光的近场 $\left|V\right|$ 阶空间相干函数 [9] 是：

$\begin{array}{c}{\Gamma }^{\left(\left|V\right|\right)}\left(q_1,z_1;\cdots ;q_{\left|V\right|},z_{\left|V\right|}\right)=\langle E^{*}\left(q_1,z_1\right)E\left(q_1,z_1\right)E^{*}\left(q_2,z_2\right)E\left(q_2,z_2\right)\cdots E^{*}\left(q_{\left|V\right|},z_{\left|V\right|}\right)E\left(q_{\left|V\right|},z_{\left|V\right|}\right)\rangle \\ \simeq {\displaystyle \underset{j,k,l,\cdots }{\sum }{\left|\frac{1}{\sqrt{\left|V\right|!}}{\displaystyle \underset{\left|V\right|!}{\sum }\left(E_{j1}{E}_{k2}{E}_{l3}\cdots \right)}\right|}^2}.\end{array}$

文献 [9] 中测量了热光的非平庸三阶相干函数，并且有一系列不寻常和有趣的性质，实验结果和理论模拟的结果在统计误差范围内符合得很好，用类似的方法也可以对于 $\left|V\right|$ 个成像系统的高阶相干性进行实验检验其正确性。设第u个成像系统的格林函数是：

$\begin{array}{c}g\left(k,\omega ;q_{wu},z_u=s_{ou}+s_{iu}\right)=\frac{-{\omega }^2}{{\left(2\pi c\right)}^2{s}_{ou}{s}_{iu}}{\text{e}}^{i\frac{\omega }{c}\left(s_{ou}+s_{iu}\right)}G\left(\left|q_{wu}\right|,\frac{\omega }{c{s}_{iu}}\right){\displaystyle {\int }_{obj}\text{d}{q}_{ou}}A\left(q_{ou}\right)G\left(\left|q_{ou}\right|,\frac{\omega }{c{s}_{ou}}\right){\text{e}}^{ik·q_{ou}}\\ \times {\displaystyle {\int }_{lens}\text{d}{q}_{lu}}G\left[\left|q_{lu}\right|,\frac{\omega }{c}\left(\frac{1}{s_{ou}}+\frac{1}{s_{iu}}-\frac{1}{f_u}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_o}{s_{ou}}+\frac{q_{wu}}{s_{iu}}\right)·q_{lu}},\end{array}$

${\displaystyle {\int }_{lens}\text{d}{q}_{lu}}G\left[\left|q_{lu}\right|,\frac{\omega }{c}\left(\frac{1}{s_{ou}}+\frac{1}{s_{iu}}-\frac{1}{f_u}\right)\right]{\text{e}}^{-i\frac{\omega }{c}\left(\frac{q_{ou}}{s_{ou}}+\frac{q_{wu}}{s_{iu}}\right)·q_{lu}}\propto somb\left(\frac{R}{s_o}\frac{\omega }{c}\left|q_{ou}+\frac{q_{wu}}{m_u}\right|\right).$

其中 $q_{ou}$ 、 $q_{lu}$ 和 $q_{wu}$ 分别是物平面、透镜平面和像平面上的二维坐标向量， $m_u=\frac{s_{iu}}{s_{ou}}$ 是第u个成像系统的放大率。对于连通图 $G=G\left(V,E\right)$ ，由文献 [9] 的三阶空间相干函数得到热光的近场 $\left|V\right|$ 阶空间相干函数：

$\begin{array}{l}{\Gamma }^{\left(\left|V\right|\right)}\left(q_{w1},z_1;\cdots ;q_{w\left|V\right|},z_{\left|V\right|}\right)\\ \simeq {\displaystyle \underset{U\subset V}{\sum }[{\displaystyle \underset{b\in U}{\prod }{\left|{\displaystyle \int \text{d}kg\left(k;q_{wb},z_b\right)}\right|}^2}({\displaystyle \underset{\left(u,v\right)\in E_U}{\prod }{\displaystyle \int \text{d}k}{g}^{*}\left(k;q_{wu},z_u\right)g\left(k;q_{wv},z_v\right)}}\\ +{\displaystyle \underset{\left(u,v\right)\in E_U}{\prod }{\displaystyle \int \text{d}k}g\left(k;q_{wu},z_u\right)g^{*}\left(k;q_{wv},z_v\right)})]\\ \propto {\displaystyle \underset{U\subset V}{\sum }{\displaystyle \underset{\left(u,v\right)\in E_U}{\prod }{\Gamma }_{uv}^{\left(1\right)}\left(q_{wu},z_u;q_{wv},z_v\right)}}.\end{array}$

对于任意的节点 $u,v\in V$ ，设 $s_{ou}=s_{ov}=s_o,s_{iu}=s_{iv}=s_i,m_u=m_v=m,f_u=f_v=f,z_u=z_v=d$ ， $\left|V\right|$ 个成像系统的光探测器位于半径为d的球面上，光场分布相同， $A\left(q_{ou}\right)=A\left(q_{ov}\right)=A\left(q_o\right)$ ，则有：

${\Gamma }_{uv}^{\left(1\right)}\left(q_{wu};q_{wv}\right)\propto {\left|{\text{e}}^{i\frac{\omega }{2c{s}_i}\left({\left|q_{wu}\right|}^2-{\left|q_{wv}\right|}^2\right)}{\displaystyle {\int }_{obj}\text{d}{q}_o}{A}^2\left(q_o\right)somb\left(\frac{R}{s_o}\frac{\omega }{c}\left|q_o+\frac{q_{wu}+q_{wv}}{2m}\right|\right)somb\left(\frac{R}{s_i}\frac{\omega }{c}\left|q_{wu}-q_{wv}\right|\right)\right|}^2.$

所以得到多视图立体成像的三维重建公式(4)。

本节得到的三维重建公式是目前为止的文献 [9] - [19] 中没有出现过的，其创新点是公式(3)和(4)。

4. 结论

本文得到多目视觉的几何学三维重建方法，由热光的近场高阶相干性测量得到立体成像的扩展函数三维重建公式，两种三维重建方法类似。文中由几何学方法得到的三维重建公式(1)和公式(2)说明人类的双眼视差有视网膜为中心的双眼视差和以头部为中心的双眼视差，根据量子光学的空间高阶相干性得到的三维重建公式(3)和公式(4)在进行光子符合成像高阶空间相干性测量时就能够进行快速自动立体匹配，这与人类双目立体视觉和昆虫复眼的立体匹配原理一致，将来可以用类似于量子“鬼”成像的实验方法验证文中给出三维重建公式的正确性，并且预期能够会得到许多有趣的实验结果。

基金项目

山东省本科教学改革资助项目(Z2021114)。

参考文献