基于改进K-Means聚类算法和最小生成树融合模型的配电网规划研究

Research on Distribution Network Planning Based on Improved K-Means Clustering Algorithm and Minimum Spanning Tree Fusion Model

摘要: 本文针对配电网在规划分区时各分区用户负荷差值较大而造成可靠性不足和经济损失等问题，分别提出了一种基于负荷因子的平衡负荷初步分区方法和基于欧式距离权重的改进K-means聚类算法，并将其应用于配电网规划研究。以我国某城市街道为例，试验结果表明改进的K-means聚类在负荷分区的均匀分布上优于传统的K-means聚类方法，改进的K-means聚类负荷差值的平均值由0.364MW下降到0.1675 MW。输出聚类结果后的最短路径以实现配电网规划线路图。

Abstract: This article proposes a preliminary balanced load partitioning method based on load factors and an improved K-means clustering algorithm based on Euclidean distance weights to address the issues of insufficient reliability and economic losses caused by large differences in user loads between different zones in distribution network planning. These methods are applied to research on distribution network planning. Taking a certain urban street in China as an example, the experimental results show that the improved K-means clustering is superior to the traditional K-means clustering method in terms of uniform distribution of load zones. The average value of the improved K-means clustering load difference decreases from 0.364 MW to 0.1675 MW. The shortest path after clustering results is output to achieve distribution network planning circuit diagram.

1. 引言

配电网规划是指根据一段时期内该区域用户点的负荷预测和已有电网的基本情况，在满足当期内一定负荷增长和安全可靠供电的前提下，确定最优且可行的电网设备建设方案，使得配电网的投资建设成本和运行费用最小 [1] [2] [3] 。早期用相对传统的数学规划方法来解决配电网规划问题，例如动态规划法 [4] 、线性规划法 [5] 和层次分析法 [6] 等。随着计算机科学技术的发展，一些依赖于强大计算能力的解决方法被提出。如遗传算法 [7] 、粒子群算法 [8] 、蚁群算法 [9] 等，针对各种组合优化问题，该算法都已经实证了自身的优点。

但随着城镇化进程的加快，用电负荷的急剧增加，配电网的规模也越来越大，同时各变电站和电源用户数量庞大且分布杂乱无章。直接考虑配电网的所有负荷点会导致决策变量过多，计算难度较大等问题。因此，有必要在实施配电网规划前进行合理的分区规划。徐芮等 [10] 提出了采用K-means聚类算法对负荷点进行聚类分区的配电网规划技术，并将聚类中心作为等效负荷点，进行各分区的主次级网架和各分区内的联络线规划。董秋仙等 [11] 选取最大相异度参数值所对应的样本作为初始聚类中心。但这些方法都没有考虑到负荷分布不均匀对分区的影响，出现了一些分区负荷较重而一些分区负荷较轻的情况，不利于系统的经济运行。

为了避免上述问题，同时减少计算困难，本文分别提出了一种基于负荷因子的负荷平衡的初步分区方法和基于欧式距离权重的改进K-means聚类算法应用于配电网规划研究，以此来解决在规划分区时各分区用户负荷差值较大而造成可靠性不足和经济损失的问题。并结合最小生成树算法，输出聚类结果后的最短路径以实现配电网规划线路图，增强城市街道配电网规划研究可视化效果。

2. K-Means聚类算法

聚类是针对给定的样本，依据它们特征的相似度或距离，将其归并到若干个“类”或“簇”的数据分析问题，其目的是通过得到的类或簇来发现数据的特点或对数据进行处理，在数据挖掘、模式识别等领域有着广泛应用 [12] [13] 。随着数据分析领域的不断发展，更多较好的数据分析方法不断被提出，例如K-means、K-MS、ET-SSE等 [14] [15] [16] 。其中K-means聚类算法又称K-均值聚类算法，k-均值算法源于信号处理中的一种向量量化方法，现在则更多地作为一种聚类分析方法流行于数据挖掘领域，由于其具有运算速度快、可解释性强等优点，因此在数据挖掘、图像处理、自然语言处理领域都有着重要应用 [17] [18] [19] 。

K-means聚类算法是基于原型目标函数的硬聚类算法。K-means聚类算法定义观测集 $\left(x_1,x_2,\cdots ,x_n\right)$ ，其中每个观测值都是一个d-维实向量，k-均值聚类要把这n观测值划分到k个集合中(k ≤ n)，使得组内平方和(WCSS within-cluster sum of squares)最小。换句话说，它的目标是找到使得下式满足的聚类 $S_i$ ：其中 ${\mu }_i$ 是 $S_i$ 中所有点的均值。

$\arg \underset{s}{\min }{\displaystyle \underset{i=1}{\overset{k}{\sum }}{\displaystyle \underset{X\in S_i}{\sum }{\Vert X-{\mu }_i\Vert }^2}}$ (1)

算法按照下面两个步骤交替进行：

1) 分配(Assignment)：将每个观测分配到聚类中，使得组内平方和(WCSS)达到最小。因为这一平方和就是平方后的欧式距离，所以很直观地把观测分配到离它最近的均值点即可：

$S_i^{\left(t\right)}=\left\{x_p:{\Vert x_p-m_i^{\left(t\right)}\Vert }^2\le {\Vert x_p-m_j^{\left(t\right)}\Vert }^2\forall j,1\le j\le k\right\}$ (2)

其中，每个 $x_p$ 都只被分配到一个聚类 $s^t$ 中，尽管在理论上它可能被分配到2个或者更多的聚类。

2) 更新(Update)：对于上一步得到的每一个聚类，以聚类中观测值的质心(centroids)作为新的均值点：

$m_i^{\left(t+1\right)}=\frac{1}{\left|S_i^{\left(t\right)}\right|}{\displaystyle \underset{x_j\in S_i^{\left(t\right)}}{\sum }{x}_j}$ (3)

因为算术平均是最小二乘估计，所以这一步同样减少了目标函数组内平方和(WCSS)的值。这一算法将在对于观测的分配不再变化时收敛。由于交替进行的两个步骤都会减少目标函数WCSS的值，并且分配方案只有有限种，所以算法一定会收敛于某一最优解。

K-均值聚类算法的目标函数是组内平方和(WCSS)，而且按照“最小二乘和”来分配观测，确实是等价于按照最小欧氏距离来分配观测的。但是在配电网规划领域所要解决的不仅仅是简单的“距离问题”，还要将各个用户的负荷考虑进去以避免电源点的供电容量不足以支撑负荷点的需求总量等问题。因此，需要对现有的K-均值聚类方法进行改进，才能更好地应用在配电网规划领域。

3. 最小生成树算法

最小生成树(Minimal Spanning Tree, MST)是基于图论的相关知识而发展起来的一种求解各点之间最小权重和、且两点之间只有一条通路的方法。具体来看，在一个给定的无向图G = (V, E)中，V表示顶点的集合，E表示边的集合，(u, v)代表连接顶点u与顶点v的边，而w(u, v)表示此边的权重，若存在T为E的子集且为无循环图，使得联通所有结点的权重之和w(T)最小，则此T即为无向图G的最小生成树。

常用的求解最小生成树问题的方法有Kruskal算法、Prim算法，其基本步骤就是每一步都从未选择的边中选取一条边e，使之与已选边不构成“圈”，且e是未选边中权重最小的，直到选够n − 1条边为止。具体操作如下：

1) 将所求规划问题模拟成二维无向图；

2) 把图上的每一条边存在一个数组中，数组中的每个元素均含有起点、终点、权重三个单元；

3) 将边数组按权重从小到大排序；

4) 依次按边的权重从小到大枚举每一条边，如果边的两个端点已经连通了，则跳过该边(通过并查集判断)；

5) 否则将该边加入“生成树”中，并将该边的两个端点也加入并查集中；

6) 返回第4)步，直到选够n − 1条边为止。

可将本文的配电网规划简化成带权重的最短路径问题，本文最小生成树主要应用于聚类之后寻求各个用户与电源点之间的最短路径问题，得到配电网规划方案。

4. 基于改进K-Means聚类算法和最小生成树融合方法

4.1. 双供配电网初步分区

本文研究的是双供配电网规划，当已知两个电源和一批用户的平面坐标、每个用户的用电需求。需要设计两个单供配电网，本题初步考虑传统的K-Means聚类算法，若通过欧式距离最小原则进行负荷点聚类分区，会出现两个分区负载不均衡进而导致系统运行不经济的问题，同时也会使得两个分区间的联络线的备用容量增大，投资成本增加。所以针对此问题，本文提出了一种基于负荷因子的负荷平衡的初步分区方法。

针对已知的用户坐标信息，分别计算所有用户到两个电源点的欧氏距离，根据距离最小原则初步把所有用户分给两个电源，电源1所在分区记为分区一，电源2所在分区记为分区二。在此基础上，我们引入一种负荷因子，取负荷因子为0.01，load_all为用户总负荷值，当 $\left|{\text{load}}_1-{\text{load}}_2\right|>0.01\ast \text{load\_all}$ 时，进行迭代操作，标签为1的改为2，直到此循环终止。此时可达到了分区负荷均衡的效果。

双供配电网初步分区方法的伪代码如下所示：

分区结束后可进行单个电源点的配电网规划，传统的K-means聚类是通过各点到聚类中心点距离最小的原则进行负荷点的聚类分区，当各个负荷点的负荷大小差异较大时，传统的K-means聚类方法可能失效，因为此时电源点的供电容量不足以支撑负荷点的需求总量，因此会产生扩展供量提高投资成本。较好的解决办法是在对各个负荷点进行聚类分区时将各个负荷点的负荷大小考虑进对聚类产生的影响中，可有效地解决负荷分布不均匀引起的负荷点聚类分区之间的负荷相差较大的问题。本文对K-means聚类进行改进，结合现有数据特点将各个负荷点的负荷大小转变成相应的权重加入到聚类中心点欧式距离的判别中。第j个负荷点的负荷权重 ${\alpha }_j$ 计算公式如下：

${\alpha }_j=\frac{p_j}{{\displaystyle \sum p_j}}$ (4)

式中，j为负荷点的编号， ${\alpha }_j$ 是第j个负荷点的权重， $p_j$ 为第j个负荷点的负荷大小。

在负荷点分布不均匀时，引入权重变量可增大负荷密度较小区域的负荷点聚类分区的负荷点个数，减小负荷密度较大区域的负荷点聚类分区的负荷点个数，从而在一定程度上实现各负荷点聚类分区之间的负荷相对均匀，可进一步节省联络线投资以提高网络架构规划的整体经济性。

4.2. 改进的K-Means聚类方法基本步骤

1) 确定负荷点聚类分区个数k

本文采用WGSS的碎石图来寻找最优的K，目标是使得WGSS达到足够小。目标函数如下：

$\text{WGSS}={\displaystyle \underset{j=1}{\overset{p}{\sum }}{\displaystyle \underset{l=1}{\overset{k}{\sum }}{\displaystyle \underset{i\in G_l}{\sum }{\left(y_i-{\bar{y}}_j^{\left(l\right)}\right)}^2}}}={\displaystyle \underset{l=1}{\overset{k}{\sum }}{\displaystyle \underset{i\in G_l}{\sum }{\left(y_i-{\bar{y}}^{\left(l\right)}\right)}^{\prime }\left(y_i-{\bar{y}}^{\left(l\right)}\right)}}$ (5)

其中，WGSS (族群内方差)可理解为每个点到其簇(最终聚类)的质心的距离之和， $G_j$ 为第j个族群， ${\bar{y}}^{\left(l\right)}={\displaystyle {\sum }_{i\in G_l}{y}_{ij}/n_i}$ 是族群 $G_j$ 中变量j的均值， $y_i={\left(y_{i1},\cdots ,y_{ip}\right)}^{\prime }$ ， ${\bar{y}}^{\left(l\right)}={\left({\bar{y}}_1^{\left(l\right)},\cdots ,{\bar{y}}_p^{\left(l\right)}\right)}^{\prime }$ 。

根据上面的式子我们知道，当k = n (即每个族群只有一个点)的时候，WGSS = 0，即组内方差平方和最小。但是这个时候就是一个过拟合的现象。也就是说，我们的目标是选择一个使得WGSS足够小(但不是最小)的k值，通常选取拐点(knee point)为最优的k值。

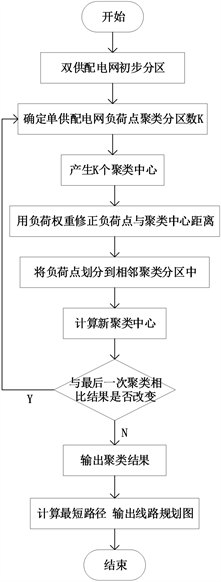
Figure 1. Flow chart of partition planning method

图1. 分区规划方法流程图

2) 确定聚类中心

从包含n个样本的集合中随机挑选出k个样本，作为k个初始的聚类中心。

3) 计算用户之间的修正加权欧氏距离

计算所有样本到各个初始聚类中心的修正的加权欧式距离，并按照距离最小的原则划分给不同的类中心。其中修正的加权欧式距离定义如下：

$\min d_{lj}={\alpha }_j\sqrt{{\left(x_l-x_j\right)}^2+{\left(y_l-y_j\right)}^2}$ (6)

式中， $d_{lj}$ 为第l个负荷点聚类分区的聚类中心和第j个负荷点之间的修正距离；负荷点j的权重 ${\alpha }_j$ 由式(公式4)计算； $\left(x_l,y_l\right)$ 和 $\left(x_j,y_j\right)$ 分别为第l个负荷点聚类分区的聚类中心和第j个负荷点的坐标。

4) 聚类完成

所有样本划分结束之后，计算每个类划分的新的聚类中心，然后重复步骤3)和步骤4)，直到相邻两次的聚类中心不再发生变化或满足设定的终止条件。

于配电网的规划而言，由于分布式电源的接入，得以更好地应对用户负荷增长的需求。而根据负荷点之间的距离大小进行聚类并设置电源或变压器，会更加节省线路的建造成本和后期的维护费用。因此，本文考虑可以用改进的K-means算法先对用户点进行聚类，并找到类中心。

综上，基于改进K-means聚类算法的分区规划方法的流程如图1所示。

5. 实例分析

下表是我国某城市的实际街道，包含2个电源(编号1和编号28)、36个用户点。各负荷点的大小及坐标见表1。

Table 1. User information of dual power supply and single supply distribution network

表1. 双电源单供配电网用户信息

首先利用本文提出了一种基于负荷因子的负荷平衡K-均值聚类初步分区方法。将两个电源点分别分为两个分区，并使之达到分区负荷均衡的效果。得到各个分区的负荷值总和，如表2所示：

Table 2. Preliminary zoning results

表2. 初步分区结果

对比分析可知，采用基于负荷因子的负荷平衡K-均值聚类初步分区方法进行初步分区时会使得不同分区之间负荷分布更加均匀，使得配电网运行更加可靠。此时，1、3、5、7、9、10、11、13、14、26、31、34、2、30、32、35、36、37号用户被划分到分区一；28、4、25、38、17、21、22、27、33、8、15、18、19、20、24、6、12、16、23、29号用户被划分到分区二。

以分区一为例分别应用传统的K-means聚类和改进的K-means聚类算法进行聚类分析，输出总负荷和负荷差值，具体数值如表3和表4所示。采用改进的K-means聚类算法时各聚类分区之间的负荷差值最大为0.286 MW，最小为0.049；而采用传统的K-means聚类算法来看，各聚类分区之间的负荷差值最大为0.639，最小为0.089。与传统K-means聚类算法相比，改进的K-means聚类负荷差值的平均值由0.364 MW下降到0.1675 MW。

Table 3. Comparison of total load results in cluster partitions

表3. 聚类分区总负荷结果对比

Table 4. Comparison of total load differences in cluster partitions

表4. 聚类分区总负荷差值对比

由对比分析可知，改进的K-means聚类算法应用到配电网规划时，可有效地解决负荷分布不均匀引起的负荷点聚类分区之间的负荷相差较大的问题，进一步提高用户用电的稳定性和规划方案的经济性。

下面将改进的K-means聚类算法的分区一和分区二的聚类结果进行进一步的规划研究，利用最小生成树算法找到各用户之间的最短路径以获取分区规划效果图并输出各个分叉点的坐标。如图2所示，1号和28号为电源点，m1，m2，m3，n1，n2，n3，n4为分区一、二的聚类中心点。红色线段为配电网的主线，黑色线段为各分区的支线，各聚类中心的坐标如表5所示。

Figure 2. Partition planning effect

图2. 分区规划效果图

Table 5. Bifurcation point coordinates for dual power supply and single supply distribution network planning

表5. 双电源单供配电网规划的分叉点坐标

6. 结论

本文分别提出了一种基于负荷因子的负荷平衡的初步分区方法和基于欧式距离权重的改进K-means聚类算法应用于配电网规划研究，以此来解决在规划分区时各分区用户负荷差值较大而造成可靠性不足和经济损失的问题，试验结果表明改进的K-means聚类在负荷分区的均匀分布上优于传统的K-means聚类方法。将其应用于实际街道中，结合最小生成树算法，输出聚类结果后的最短路径以实现配电网规划线路图，增强城市街道配电网规划研究的可视化作用，使能够更清晰地理解配电线路与用户之间的拓扑连接关系、更加直观地理解配电网规划研究的过程。

参考文献