1. 引言
随着我国经济稳步发展,生产生活用电需求快速增长,全国发电量、最高用电负荷不断突破历史峰值,特别是迎峰度夏期间,随着气温攀升,负荷高峰时刻电力供应形式十分严峻 [1] 。水电作为一种清洁、可再生的能源,在电力系统中发挥着重要的作用,是很多地区电网迎峰度夏的骨干核心电源 [2] [3] ,承担着顶峰发电、缓解高峰供电压力的关键任务。在大规模风光电源并网以及迎峰度夏期间高峰供电紧张的情况下,充分利用水电良好的调节性能,准确分析水电站群顶峰能力,对于保障电网的可靠运行和清洁能源消纳至关重要 [4] 。
近些年,国内外学者在水电调峰和迎峰度夏方面已经开展了大量的研究。对于这类问题的处理,大致可以分为两种方向,一种是对模型的精确描述和构建,致力于通过建立数学优化模型解决水电站调度问题:例如,Liu等 [5] 提出了梯级水电短期多电网调峰模型,充分利用水电的灵活性,有效降低了系统碳排放;谭晶等 [6] 建立了梯级水电调峰的分布鲁棒优化调度模型,同时考虑了光伏发电具有的随机性以及直流外送的运行方式,有效促进了清洁能源消纳;另一种方向是从求解策略方面进行改进,以提高计算速度和精度:例如,李树山等 [7] 提出了一种复杂约束归一化处理策略的梯级水电短期调峰调度方法,有效解决了水电调峰时众多复杂约束带来的求解困难问题;Jiang等 [8] 利用深度学习方法解决了水电站短期优化调度问题,并讨论了模型在夏季汛期的表现,验证了水电在提升系统汛期电力供应方面的出色表现。
上述研究主要集中在日前调度,但在电力系统灵活性资源缺乏、电网调峰压力越来越大的情况下,如何评估较长时间周期的水电顶峰能力对于迎峰度夏运行方式安排,保障电力系统安全稳定运行至关重要。为此,本文以我国西南某地区水电站群为依托,考虑夏季迎峰度夏电量需求、日内顶峰能力需求,以及各水电站的水位、来水预测、期末蓄能等情况,建立了水电站群中期顶峰能力分析模型。并提出了一种基于水电站日内最大发电能力试算模型、水电站运行方式动态分类调整的快速求解方法,通过日电量分配滚动计算实现模型的高效求解,最后,以实例研究验证了所提模型方法的有效性和实用性。
2. 迎峰度夏水电顶峰问题
高温大负荷是我国大部分地区迎峰度夏运行方式的基本特点,充分合理的利用水电的灵活性调节能力,以满足高峰负荷需求,是电力调度部门每年夏季面临的严峻挑战。分析水电中期顶峰能力直接关系到电网较长时间安全稳定运行,该问题可描述为:根据电网测算的对统调水电站每日总电量需求以及预计的各电站来水情况,利用水电灵活调节能力,合理安排水电站群每日发电计划,一方面尽量满足调度期内每日电量需求 [9] ,另一方面在日内将水电尽量安排在顶峰时段发电,以缓解电网高峰供电压力 [10] 。
为保证电网安全稳定运行,在调度计划制作中,需要考虑多种水力、电力约束:
1) 日电量计划约束:
(1)
式中,
表示参与计算的水电在第t日的总计划电量,MW·h;
表示水电站m在第t日的平均出力,MW;M表示统调季调节以上水电站的总数;
表示每日小时数,h;
、
分别表示第t日的大、小水电发电量,其中小水电每日出力过程按照预测值给定。
2) 水量平衡约束:
(2)
式中,
和
和分别表示水库m在t时段初和时段末的库容,m3;
表示水库m在t时段的总入库流量,m3/s;
表示水库m在t时段的发电引用流量,m3/s;
表示水库m在t时段的弃水流量,m3/s。
3) 初始水位约束:
(3)
式中,
表示水库m的初始库容,m3。
4) 水电顶峰时长约束:
水电站在运行时一般承担系统峰荷,在系统负荷高峰时按照最大发电能力运行,在负荷低谷时按照最小生态流量发电运行,出力过程大致呈现“几”字形(如图1所示)。水电站顶峰发电的时长受系统负荷峰谷过程影响,存在一个上下限:
(4)
式中,
、
以及
分别表示水电顶峰小时数及其下限和上限,h。由于一年内不同季节系统负荷的典型特征不同,水电站参与顶峰的时长也不同 [11] ,可根据历史运行数据确定。
5) 库水位约束:
(5)
式中,
、
和
分别表示水库m在t日的库水位及其下限和上限,m。
6) 发电流量约束:
(6)
式中,
和
分别表示水电站m在t日的发电流量下限和上限,m3/s。
7) 出库流量约束:
(7)
式中:
、
和
分别表示水电站m在t日的出库流量及其下限和上限,m3/s。
8) 电站出力约束:
(8)
式中,
和
分别表示水电站m在t日的出力下限和上限,MW。
9) 水位库容约束:
(9)
式中,
表示水库m的水位库容关系,是一维非线性函数。
10) 尾水位泄量约束:
(10)
式中,
表示水库m在t日的下游尾水位,m;
表示水库m的尾水位泄量关系,是一维非线性函数。
11) 电站出力特性约束:
(11)
(12)
(13)
式中,
表示水电站m的出力特性,是一个关于发电流量
以及净水头
的二维非线性函数;
表示t日水电站m的水头损失,m;
、
以及
表示水电站m的水头损失系数和水头损失常数。

Figure 1. Schematic diagram of daily peak power generation of hydropower station
图1. 水电站日内顶峰发电示意图
3. 水电顶峰求解方法
3.1. 总体思路
上述模型包含众多水力、电力约束,常规方法难以求解 [12] 。本文提出了一种电站发电能力试算及滚动分类的策略,逐日测算水电站的电力电量供应情况,并进行分类,有效降低问题的维度。具体流程如图2所示,总体步骤如下:
1) 最大发电能力试算:给定初始电站顶峰小时数,试算水电站日内最大发电能力及对应发电流量。将顶峰发电流量作为变量,对该日电站的最大发电能力进行试算。

Figure 1. Diagram of overall solution approach
图1. 总体求解思路
2) 电站运行方式动态分类。基于上述水电站最大发电能力试算方法,对水电站进行分类:若电站能从当前计算时段每日按照顶峰小时数上限运行至调度期末,则将该类型电站划分为II类电站,相应的剩余日期均按照最大顶峰小时数运行;其余电站划分为I类电站,每日顶峰时长根据剩余电量计划进行确定。
3) 电量分配滚动计算。从首日开始,对电站进行划分,其中,II类电站按照最大发电能力运行,若能够满足日电量计划,则计算下一日;若不能满足电量计划,则需I类电站参与电量分配,每个电站承担的电量比例根据该日允许最大发电量的比例确定。通过逐日滚动计算,从而实现计算时段内的电量分配。
3.2. 水电站日内最大发电能力试算
水电站的发电能力受净水头影响,当水头较高时,电站能够以装机容量运行,且此时发电流量一般小于水轮机最大过流能力;当水头较低时,因水头受阻,最大发电能力一般小于装机容量。在给定水电站当日的顶峰小时数
后,可将顶峰时的发电流量作为变量,对其发电流量和最大发电能力进行试算:
1) 首先,假设顶峰发电流量
等于水电站最大发电流量
;
2) 已知初始水位、顶峰时长以及电站生态流量或最小出力要求,由水量平衡方程可以得到该日的末库容。其中,日出库水量
;
3) 再根据公式(9)~(13)以水定电计算得到该日的平均水头、水电站的顶峰出力
及此时的顶峰发电流量
;
4) 若
与
之间的误差超出允许范围,则令
,重复步骤2~4;若小于误差允许范围,则得到该顶峰小时数下的顶峰出力
及对应发电流量
。
3.3. 水电站运行方式动态分类
为了提高求解效率,首先按照对各个电站的发电能力进行分析并划分类别。由于水电站发电能力受电站调节能力以及来水影响较大,部分调蓄能力较强或来水较好的水电站能够在各日均以顶峰小时数上限运行,则这类电站划分为一类,其每日顶峰小时数按照顶峰小时数上限运行,不再进行滚动计算,其余电站按可发电量的比例参与剩余电量的分配。上述方法可以极大的降低计算量,从而在满足多种水力电力约束下实现高效求解。
在对某日的电站运行状态进行划分时,假设电站从该日至期末各日均以顶峰小时数上限运行,采用上节中的试算方法对逐个电站进行计算,若电站能够正常运行至期末,则此类电站被划分为II类电站,其之后每日的顶峰出力、顶峰发电流量以及顶峰小时数均确定。若电站不能够正常运行至期末,在调度期内某天破坏了水位约束条件,则说明该电站不能始终按照顶峰小时数上限运行,每日的顶峰时长需要进行调整,该电站划分为I类电站。I类电站的顶峰时长根据该日的电量计划确定。
3.4. 电量分配滚动计算
水电站的电量分配由首日到期末逐日进行滚动计算,首先根据上节所述的分类方法对电站进行划分,若II类电站能够满足该日电量计划,则其余I类电站蓄水不发电;否则需要I类电站承担电量计划如下:
(14)
式中,
表示I类电站t日任务发电量,即
;
表示II类电站的发电量,即
,
、
分别为I类和II类电站集合。
在I类电站电量分配时,按照当日最大可发电量的比例进行:
(15)
(16)
式中,
表示水电站m在t日的最大可发电量。
在确定日电量之后,电站具体的顶峰过程根据以电定水试算得到。计算时,以该日平均发电流量作为变量,首先给定初始值,得到该日平均水位及水头,日均水头确定,出力特性表现为发电流量的一维函数,进而计算出该日的平均出力及发电量,再调整平均流量值重新计算,直到电量误差满足要求。
在实际电量分配过程中,若电站分配得到的电量
,则该电站顶峰时按照最大发电能力运行,顶峰小时数
;若电量不能满足顶峰小时数下限运行,则降低顶峰出力,保证顶峰小时数
,此时
。
4. 算例分析
水电作为优秀的调节电源,经常承担电网调峰、调频任务,充分发挥水电的灵活性,对于保障电力供应以及提高系统经济性具有重要意义。本文以西南某地区14座季调节及以上水电站群作为主要研究对象,对模型进行验证。其中,各个电站的参数如表1所示。设置各个电站顶峰小时数下限及上限分别
,
,给定未来15日的电量需求以及各个电站日平均区间流量,计算电站的顶峰能力。

Table 1. Parameters of hydropower plants
表1. 电站基本参数
选择夏季50%来水保证率下的场景作为算例,各个电站的入库流量见附录表A1,计算得到各电站每日电量过程以及系统电量需求如图3所示。从图中可以看出,前13日均能按照电网电量计划运行,后2日由于来水不足,无法支撑电量计划。
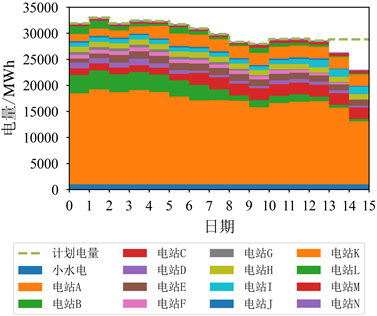
Figure 3. Daily supply of hydroelectricity
图3. 水电电量每日供应情况
在顶峰能力方面,图4给出了各电站逐日顶峰出力情况,从图中可以看出,每日平均顶峰小时数稳定在11小时左右,最高顶峰能力接近3000 MW,能够有效实现水电顶峰。但水电实际顶峰情况受电站A的影响较大,因为其装机容量较大且调节能力较强,占参与计算电站总装机的58%。在调度周期最后2日,由于来水量不足,水电顶峰能力和顶峰时长受到影响较大,部分电站降低至最小顶峰小时数运行,产生了比较瘦的高峰,以尽量满足尖峰负荷需求。
在各个电站运行过程方面,根据前述求解方法,可以对电站进行类型划分,其中具有典型代表性的3种电站如图5所示。可以看出,各个电站调度期内运行方式各不相同,具体分析如下:
水电站A有最小生态流量要求,相应存在基荷出力,且调度期库水位逐渐下降,水头降低,最大顶峰出力逐渐下降。另外,该电站在最后2日顶峰时长迅速下降,因为水位已达到水位下限,发电量取决于来水量,入库流量较小,则顶峰时长较短。
水电站H水量充足,能够始终以顶峰小时数上限运行,水位不断下降。即水电站H被划分为II类电站,在调度期内每日均以顶峰小时数上限运行。
水电站C水量不足以保证每日均以顶峰小时数上限运行,但在滚动计算过程中,第7日之后电站来水增大,能够保证7~15日以顶峰小时数上限运行。故从第7日起,水电站C的类型从I类转变为II类,后续日期直接按照最高顶峰小时数运行,不再参与出力分配,能够大幅减少总体计算量。

(a) 水电站A
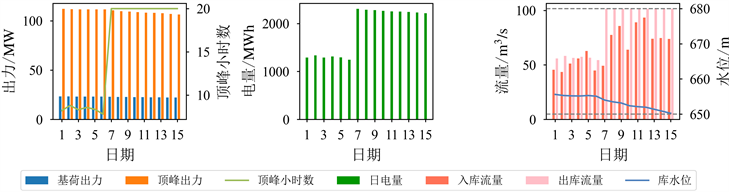 (b) 水电站C
(b) 水电站C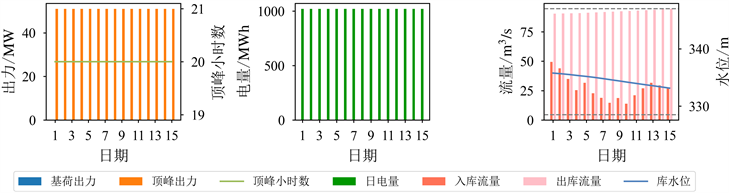 (c) 水电站H
(c) 水电站H
Figure 5. Results of typical hydropower stations
图5. 典型电站计算结果
为了进一步验证本文所提方法的有效性,对25%和75%两种来水保证率场景进行分析,入库流量分别见附表A2、A3,得到两种场景下的结果如图6所示。可以看出,在来水较多时,水电系统各日均能满足电量计划,可以考虑增加系统电量计划,承担更多的系统调峰发电任务;在来水较少时,水电系统仅在前几日能够满足电量计划,水位降至最低限制水位,之后只能依靠来水进行发电。
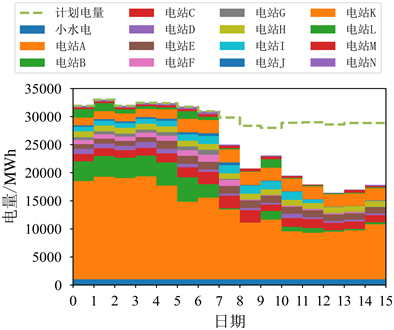
 (a) 25%保证率来水场景(b) 75%保证率来水场景
(a) 25%保证率来水场景(b) 75%保证率来水场景
Figure 6. Electricity supply for different typical inflow scenarios
图6. 不同典型来水场景电量供应情况
综合不同来水情况下电站的运行方式,可以看出,模型中电量供应能力较强的电站优先承担计划任务,使得电站能够减少弃水、窝电,保证系统电量供应。此外,系统电量供应能力受调节能力较强的电站(如电站A)影响较大,因此,在后续研究中可以充分发挥其电量供应以及水量调节的重要作用,在水量充足时尽量让其余小电站承担更多电量,使大电站能够保持高水位运行,增加发电效率,在后续来水量不足时顶峰发电,以保障电网安全稳定。
总体上,除满足生态流量等最低流量要求外,本文所提方法得到的水电出力能够集中在顶峰时段,具体执行时,可以根据电网负荷特性,将顶峰时段划分为多个区间,充分利用水电缓解电网迎峰度夏期间的顶峰压力。另外,本算例的单次计算时间小于3 s,在实际调度过程中,一方面可以根据模型的计算结果,快速修改相关约束条件进行调整;另外一方面,在执行过程中可以逐日滚动计算,动态适应流量变化以及电网顶峰需求。因此,本文所提模型能够在较长时间周期内分析水电顶峰能力,为电网迎峰度夏提供参考。
5. 结论
本文提出了迎峰度夏期间水电中期顶峰能力分析方法,并以某地区电网水电站群实际情况为背景进行算例分析,结果表明:
1) 本文提出的模型准确描述了水电中期运行的水力、电力条件,并且能够根据上级部门下达的电量计划合理分配水电运行过程,得到逐日的顶峰出力情况,为电网迎峰度夏期间水电发电调度提供决策依据。
2) 利用提出的水电发电能力试算、运行方式动态分类以及电量分配滚动计算方法,能够实现水电顶峰模型的快速求解,有效缓解了大规模水电系统调度问题中存在的维数灾问题。
3) 所提方法能够实现水电中期调度计划的动态调整,快速分析得到水电站群电力电量持续性供给能力,可以为迎峰度夏期间水电顶峰能力分析提供动态支持。
基金项目
国家自然科学基金重点项目(52039002)。
附录
算例分析中三种不同来水场景的区间流量过程如附表A1、A2、A3所示。

Table A1. Inflowscenario under the 25% confidence level
表A1. 25%保证率场景来水

Table A2. Inflowscenario under the 50% confidence level
表A2. 50%保证率场景来水

Table A3. Inflowscenario under the 75% confidence level
表A3. 75%保证率场景来水