基于时间序列分析的新疆红枣产量预测

Prediction of Xinjiang Jujube Yield Based on Time Series Analysis

摘要: 为了有效提高新疆红枣产量的预测精度，文章构建了符合红枣产量的预测模型。运用GM模型与ARIMA模型分别对新疆红枣产量进行预测，并根据二者模型特点建立了基于灰色理论与时间序列的组合预测模型对新疆红枣产量进行了预测。根据预测结果发现，基于灰色理论与时间序列的组合模型的预测精度高，表明了基于灰色理论与时间序列的组合模型在新疆红枣产量预测方面有较高的准确性。

Abstract: In order to effectively improve the prediction accuracy of Xinjiang jujube yield, a prediction model suitable for jujube yield was constructed in this paper. The GM model and ARIMA model were used to predict the yield of Xinjiang jujube, and a combination prediction model based on grey theory and time series was established according to the characteristics of the two models to predict the yield of Xinjiang jujube. According to the prediction results, it was found that the combination mod-el based on grey theory and time series had high prediction accuracy, which indicates that the com-bination model based on grey theory and time series has high accuracy in predicting the yield of Xinjiang jujube.

1. 引言

红枣是一种温带作物，生命力顽强，能够适应强光、强辐射条件，更有耐盐碱的特质，素有“铁杆庄稼”的美称。新疆维吾尔自治区是我国红枣的主要产区之一，红枣产业已然成为脱贫致富、实现乡村振兴的支柱性产业。然而，红枣产量受多方面因素影响，构建符合红枣产量变化的预测模型，科学准确地预测红枣产量，对提升红枣产业经济效益具有重要的理论价值和实际意义。

目前在有关农产品产量的预测研究当中，单一模型以及组合模型是国内外较为广泛使用的预测方法。其中单一模型常见的方法主要有时间序列分析法、灰色预测模型、BP神经网络、VAR模型等。BP神经网络和支持向量机等预测模型存在可调参数，而可调参数的选取又是决定预测性能优劣的关键，在以往的研究中，大部分对可调参数的选取都依赖人工经验，无法实现自适应寻优。组合模型通常是将线性和非线性两种模型结合起来，通过不同的赋权方式给单一模型以权重赋值。

国内外很多学者采用ARIMA模型对数据进行预测分析，并且得到了良好的结果。王斌等 [1] 采用现代统计方法建立ARIMA预测模型，探讨运用时间序列模型进行订单预测是否可行。经过误差分析后得到，ARIMA(1, 1, 0)模型可以较好地反映电商平台灰枣订单的变化趋势。张艳艳等 [2] 以某省海域水上交通事故时间序列为例，对其季节性、周期性特征进行分析，运用ARIMA模型进行拟合预测，并与指数平滑法进行比较，以验证模型的合理性，得到了良好的效果。马晓江等 [3] 通过在分析河北省流行性腮腺炎流行特征的基础上，建立ARIMA模型，进行拟合度测评。此外，还有很多学者采用GM模型进行预测。任平等 [4] 采用灰色系统GM(1, 1)模型预测了人口、耕地以及粮食的发展趋势。李炳军等 [5] 基于GM(1, N)模型对我国粮食结构供需平衡进行了分析，发现我国主要粮食的需求量和产量逐年持续增长，但供需依然存在较大缺口。黄彭等 [6] 根据2001~2015年四川粮食产量的历史数据，建立GM(1, 1)模型，预测了2016~2018年的粮食产量。王浩等 [7] 以2004~2021年中国煤炭消费量为基础，建立了长期和短期2个GM(1, 1)模型，预测了3年的中国煤炭消费量。结果表明，短期的灰色模型拟合度好，精度达到99.36%。

为了提高模型预测的精度和准度，一些学者结合各模型的优势建立组合预测模型，得到了良好的反馈。马云倩等 [8] 首先对LASSO-GM(1, N)、GM(1, 1)、GM(1, N)以及LASSO这四种模型的预测效果进行了比较分析，并选择采用效果良好的LASSO-GM(1, N)组合模型对2020年中国粮食产量进行了预测，预测显示，未来到2020年我国粮食产量处于稳步增长的状态。吴越等 [9] 分别使用Holt两参数指数平滑法和ARIMA模型预测2019~2023年长三角地区的粮食产量，并对模型进行检验，检验结果均通过，表明长三角地区的粮食产量将保持稳定增长的趋势，预测效果理想。谭满春等 [10] 利用ARIMA模型良好的线性拟合能力和人工神经网络强大的非线性关系映射能力，把交通流时间序列看成由线性自相关结构和非线性结构两部分组成，采用ARIMA模型对交通流序列的线性部分进行预测，用人工神经网络模型对其非线性残差部分进行预测。结果表明：组合模型的预测准确性高于各自单独使用时的准确性；组合方法发挥了2种模型各自的优势，是短期交通流预测的有效方法。

综合上述分析，不同赋权方法所产生的赋权值，在组合模型中其预测的效果也不尽相同。本文采用GM(1, 1)和ARIMA模型运用相关统计软件分析得出预测结果，结合二类模型的特点选取合适赋权方式建立组合预测模型，以提高新疆红枣产量预测精度和准度。

2. 预备知识

2.1. GM(1, 1)预测模型

灰色系统理论是我国学者邓聚龙教授于1982年首先提出来的。灰色系统是指已知部分信息的样本数据所能反映的不确定性系统。灰色时间序列预测，即运用反映预测对象特征的时间序列来构造灰色模型，预测未来某一时刻的特征量。最常见的是GM(1, 1)预测模型，其建模方法是利用原始的数据序列作为解微分方程，对能近似满足微分模型构造条件的序列，产生具有很强的规律性的数据，并建立一种近似的差分方程模型，以此来预测未来的发展趋势。其模型建模步骤如下。

设原始非负数据序列为：

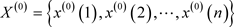
将原始非负序列经过一次累加生成可得一阶累加生成序列：

$X^{\left(\text{1}\right)}=\left\{x_{}^{\left(1\right)}\left(1\right),x_{}^{\left(\text{1}\right)}\left(2\right),\cdots ,x_{}^{\left(1\right)}\left(n\right)\right\}$

$x^{\left(1\right)}\left(k\right)={\displaystyle \underset{i=1}{\overset{k}{\sum }}{x}^{\left(\text{0}\right)}\left(i\right)},k=1,2,\cdots ,n$

作X⁽¹⁾的一阶紧邻均值生成序列Z⁽¹⁾得：

$z^{\left(\text{1}\right)}\left(k\right)=\alpha x^{\left(1\right)}\left(k-1\right)+\left(1-\alpha \right)x^{\left(1\right)}\left(k\right)\left(k=2,3,\cdots ,n\right)$

α为权重因子，一般取α = 0.5，由此可得：

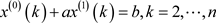
将GM(1, 1)模型的基本形式白化微分为：

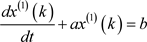
式中，a是发展系数，b是灰色作用量，a、b均表示待定参数，t表示时间。

利用最小二乘得出：

$\hat{a}={\left[a,b\right]}^T={\left(B^{T}B\right)}^{-1}{B}^{T}Y$

其中，

$B=\left[\begin{array}{ccc}-z_{}^{\left(1\right)}\left(\text{2}\right)& & 1\\ -z_{}^{\left(1\right)}\left(\text{3}\right)& & 1\\ ⋮& & ⋮\\ -z_{}^{\left(1\right)}\left(n\right)& & 1\end{array}\right],Y=\left(\begin{array}{c}{x}^{\left(\text{0}\right)}\left(\text{2}\right)\\ x^{\left(\text{0}\right)}\left(\text{3}\right)\\ ⋮\\ x^{\left(\text{0}\right)}(\; n\; )\end{array}\right)$

白化微分方程式的时间响应函数为：

${\hat{x}}_{}^{\left(1\right)}\left(k+1\right)=\left[x_{}^{\left(\text{0}\right)}\left(1\right)-\frac{b}{a}\right]{\text{e}}^{-ak}+\frac{b}{a}\left(k=1,2,\cdots ,n\right)$

经过累减，求得上式的时间响应函数为：

${\hat{x}}^{\left(\text{1}\right)}\left(k+1\right)=\left(x^{\left(\text{0}\right)}\left(\text{1}\right)-\frac{b}{a}\right){\text{e}}^{-ak}\text{+}k$

GM(1, 1)的最终模型为：

${\hat{x}}^{\left(\text{0}\right)}\left(k+1\right)={\hat{x}}^{\left(\text{1}\right)}\left(k+1\right)-{\hat{x}}^{\left(\text{1}\right)}\left(k\right)\text{=}\left(\text{1}-{\text{e}}^a\right)\left(x_{}^{\left(\text{0}\right)}\left(\text{1}\right)-\frac{b}{a}\right){\text{e}}^{-ak}$

2.2. ARIMA预测模型

ARIMA模型即差分自回归滑动平均模型，是ARMA模型(自回归滑动平均模型)的一种，属于时间序列分析。ARIMA模型通常以ARIMA(p, d, q)形式表示，AR代表“自回归项”，用p (自回归项数)定义，指用于预测下一个值的过去值；I代表“差分项”，用d (使之成为平稳序列所做的差分阶数)定义，指差分顺序规定的对序列执行差分操作的次数，是指保持平稳；MA代表“滑动平均项”，用q (滑动平均项数)定义，指预测未来值时过去预测误差的数目。ARIMA的数学形式表示为：

$\widehat{y_t}=\mu +{\phi }_1*y_{t-1}+\cdot \cdot \cdot +{\phi }_p*y_{t-p}+{\theta }_1*e_{t-1}+\cdot \cdot \cdot +{\theta }_q*e_{t-q}$

其中，φ表示AR的系数，θ表示MA的系数。

步骤1：对序列绘制自相关图和偏自相关图，进行ADF单位根检验，判断是否平稳，通过确定差分平稳确定d；

步骤2：确定p和q，拟合ARIMA模型。对平稳时间序列分别求得其自相关系数(ACF)和偏自相关系数(PACF)，观察绘图：① 若ACF在q + 1阶突然截断，则在q处截尾，判断为MA序列，② 若PACF在p处截尾，判断为AR序列，③ 若ACF和PACF皆为拖尾，判断为ARMA序列；

步骤3：参数检验，利用数理统计检验高阶模型新增加的参数是否近似为零，检验模型残差的相关特性等，利用AIC、BIC准则(既考虑拟合效果接近程度，又考虑参数个数)确定模型。

2.3. 组合预测模型

组合预测模型就是将多类单项预测模型组合起来，赋予单项模型不同权数以适当的加权平均形式得出适合的组合预测模型。基本组合预测模型为线性组合预测模型，其基本公式为：

$\widehat{y_t}={\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i}{y}_{it}={\omega }_1{y}_{1t}+{\omega }_2{y}_{2t}+\cdots +{\omega }_m{y}_{mt}\left(i=1,2,\cdots ,m;t=1,2,\cdots ,n\right)$

其中， $W={\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_m\right)}^T$ 为所赋的权重系数，且 ${\omega }_m\ge 0,{\omega }_1+{\omega }_2+\cdots +{\omega }_m=1$ ，确定权数ω要考虑误差平方和SSE最小原则： $SSE={\displaystyle \underset{t=1}{\overset{n}{\sum }}{e}_t^2}={{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left({\displaystyle \underset{i=1}{\overset{m}{\sum }}{\omega }_i{e}_{it}}\right)}}^2=W^{T}EW$ ， $E={\left(eit\right)}_{m\ast n}{\left(eit\right)}_{m\ast n}^T$ 。

通过求解线性规划问题得出最优解ω₀，R_m为元素全为1的m维行向量E为信息误差矩阵。

$\{{}_{s.t.R_{m}W=1,W\ge 0}^{\min SSE=W^{T}EW}\Rightarrow W_0=\frac{E^{-1}{R}_m^T}{R_m{E}^{-1}{R}_m^T}$

3. 实证分析

选取2011~2021年的《新疆统计年鉴》中新疆维吾尔自治区红枣产量为研究对象，对新疆红枣产量进行短期预测。

3.1. GM(1, 1)预测模型

在建立灰色预测模型GM(1, 1)前，要先对时间序列进行级比检验。若通过级比检验，则说明该序列适合构建灰色模型，若不通过级比检验，则对序列进行“平移转换”，从而使得新序列满足级比值检验。

Table 1. Grade ratio inspection

表1. 级比检验

表1展示了序列值和级比值，平移转换后序列的所有级比值都位于区间 $\left(e^{-\frac{2}{n+1}},e^{\frac{2}{n+1}}\right)$ 即(0.846, 1.181)内，说明平移转换后序列适合构建灰色预测模型。

Table 2. Model parameters

表2. 模型参数

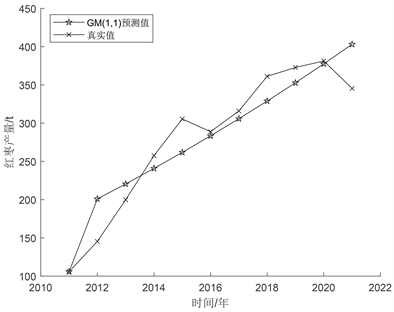
Figure 1. GM(1, 1) model prediction fitting effect diagram

图1. GM(1, 1)模型预测拟合效果图

灰色预测模型要经过检验才能判定其是否合理，只有通过检验的模型才能用来做预测，系统主要通过后验差比C值来对灰色预测模型进行检验。从表2中看出，后验差比值C值0.122小于0.35，一般后验差比值C值小于0.35则模型精度高，C值小于0.5说明模型精度合格。灰色预测模型的预测值的平均相对误差为9.77%，一般情况下小于20%即说明拟合良好。GM(1, 1)模型预测拟合效果如图1所示。

3.2. ARIMA预测模型

根据ARIMA (差分自回归滑动平均模型)的具体步骤要求，要先对数据进行ADF检验，如表3所示，分析的数据为不平稳数据。

Table 3. ADF inspection table

表3. ADF检验表

由表3可知，原序列P值为0.107大于0.05，水平上呈非显著性，接受原假设，原序列为非平稳时间序列。差分为一阶时，显著性P值为0.684大于0.05，水平上呈现非显著性，接受原假设，该序列为非平稳时间序列。在差分为二阶时，显著性P值为0.029小于0.05，水平上呈现显著性，拒绝原假设，该序列为平稳时间序列。将不平稳数据进行差分运算，得出自相关图(图2)与偏自相关图(图3)。在差分阶数为二阶时，根据数据显示结果得出：显著性P值为0.029小于5%，水平上呈现显著性，拒绝原假设，该序列为平稳的时间序列。

由图2可知，一阶自相关系数明显大于2倍标准差范围，且自相关系数衰减为小值波动的过程非常迅速，可以判断自相关图为拖尾。第2个至第10个间隔下的序列自相关系数都在置信区间内，说明序列是不相关的，但第一个间隔的相关系数超过置信区间，说明序列不是完全不相关的。由图3可看出，第一个偏自相关系数明显大于2倍标准差范围，之后的偏自相关系数都落在2倍标准差范围以内，且由非零偏自相关系数衰减为在零附近小值波动的过程非常迅速，我们可判断出偏自相关图截尾。由图2和图3与模型选择原理可以得出ARIMA模型的p、d、q值分别为2、0、0。

Figure 2. Second order auto-correlation graph

图2. 二阶自相关图

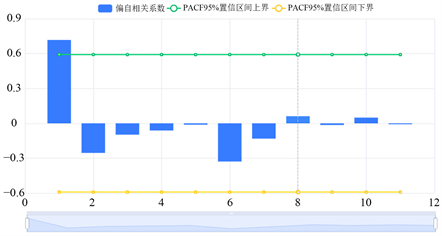
Figure 3. Second order partial auto-correlation graph

图3. 二阶偏自相关图

Table 4. ARIMA(2, 0, 0) model inspection table

表4. ARIMA(2, 0, 0)模型检验表

由表4可知，最优模型ARIMA(2, 0, 0)得出本次模型检验结果，包括样本数、自由度、Q统计量和信息准则、模型的拟合优度。从Q统计量结果分析可以得到：Q6在水平上不呈现显著性，不能拒绝模型的残差为白噪声序列的假设，同时模型的拟合优度R²为0.708，模型表现较为良好。ARIMA(2, 0, 0)模型预测值拟合效果如图4所示。

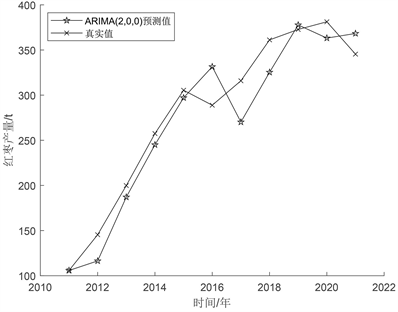
Figure 4. ARIMA(2, 0, 0) model prediction value fitting effect diagram

图4. ARIMA(2, 0, 0)模型预测值拟合效果图

由图4可知，模型被拟合后进行了残差分析，通过绘制模型的残差(观测值与模型预测值之间的差异)图(如图4所示)，可以清晰地看到自相关函数图显示残差在滞后阶数上显著不为零，说明残差之间存在自相关。残差分析是时间序列模型调优的重要步骤，有助于确保模型的可靠性和准确性。

3.3. 组合预测模型

选取2011~2021年新疆红枣产量数据作为研究对象，采用单一模型与组合模型分别预测其产量(见表5)。其中，GM(1, 1)模型的最小相对误差为0.977%，最大相对误差为38.198%，平均相对误差为9.77%；ARIMA模型的最小相对误差为1.34%，最大相对误差为19.94%，平均相对误差为7.81%；组合预测模型的最小相对误差为2.5%，最大相对误差为14.5%，平均相对误差为6.52%。比较这三者的平均相对误差，其中组合模型的平均相对误差值最小，GM(1, 1)模型的平均相对误差值最大。因此，可知组合预测模型拟合精度明显高于单一预测模型，极大地改进了单一预测模型，提高了预测精度。

Table 5. Predicted values and their predictive effects of each model

表5. 各模型预测值及其预测效果

通过构建ARIMA(差分自回归滑动平均模型)和GM(1, 1)灰色预测组合预测模型，预测出2022年到2024年的产量，组合模型预测值拟合效果如图5所示。由图5可知，组合模型预测值拟合图以一个直观的方式来展示组合模型的整体性能，实际观测值和组合模型的预测值绘制在了同一张散点图上，横轴表示实际观测值，纵轴表示组合模型的预测值，每个点代表一个数据点，观察散点分布与拟合线的关系。如图5所示，散点集中在拟合线附近并且呈现出近似45度角的趋势，说明组合模型的预测与实际观测值拟合较好。

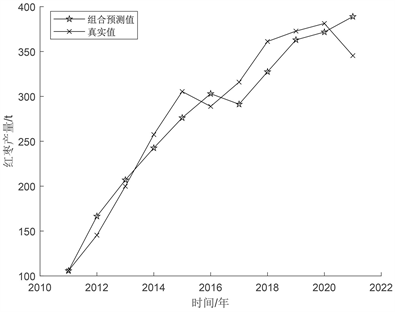
Figure 5. Combined model prediction value fitting effect diagram

图5. 组合模型预测值拟合效果图

4. 结论

本文选取了2011~2021年的《新疆统计年鉴》中新疆维吾尔自治区红枣产量年度数据为研究对象，对新疆红枣产量进行了短期预测。建立了单预测模型GM(1, 1)模型与ARIMA模型，分别对新疆红枣产量进行预测，单独采用GM(1, 1)模型与ARIMA模型进行预测时，由于各个单一预测模型存在自身条件的局限性，不能全面准确地契合原数据本身，从而降低了预测结果的精确度。建立结合GM(1, 1)模型与ARIMA模型的组合预测模型，经过实证分析结果得出组合预测模型的精度和准确度远高于单一预测模型，模型的预测拟合效果好。因此，这种组合预测模型用于新疆红枣产量预测是可行的，新疆维吾尔自治区相关部门应该根据预测相应结果积极采取一定的调控措施，科学、良好、稳步地推动新疆红枣产业迈上新台阶。

基金项目

塔里木大学大学生创新创业训练项目(编号：2023172)。