基于LSTM多步预测模型的空气质量预测与预警

Air Quality Prediction and Early Warning Based on LSTM Multi-Step Prediction Model

摘要: 本文首先通过斯皮尔曼相关性分析及灰色关联分析，以两方式相对比的方式筛选出与PM2.5浓度变化有关的因素，通过随机森林回归算法得出因素对PM2.5浓度的影响程度。然后将LSTM神经网络模型与多步预测模型相结合，构建LSTM多步预测模型，并设置步长用于预测PM2.5的值，根据均方根误差检验对模型效果进行评估。最后，将数据集带入LSTM多步预测模型并设置步长用以预测AQI的值。

Abstract: In this paper, firstly, the factors related to the changes of PM2.5 concentration are screened out by Spearman correlation analysis and grey relation analysis through two relative comparisons, and the degree of influence of the factors on the concentration of PM2.5 is derived by random forest regres-sion. Then the LSTM neural network model was combined with the multi-step prediction model to construct an LSTM multi-step prediction model and the step size was set for predicting the value of PM2.5, and the model effect was evaluated according to the root mean square error test. Finally, the dataset was brought into the LSTM multi-step prediction model and the step size was set to predict the value of AQI.

1. 引言

现代社会中，空气污染问题已经成为一个让全人类不得不重视的议题。空气中的污染物会对人类身体健康、生态环境和社会经济发展造成巨大的不利影响。为了减轻空气污染对人类生产生活造成的影响，环境空气质量指数(AQI)应运而生。通过AQI指数，可以掌握当日当地较为可靠的空气污染情况。与此同时，PM2.5是当下对人体危害最严重的空气污染物。AQI和空气中PM2.5浓度含量能对生产、环境保护等方面产生重要影响。因此，能否精准预测PM2.5浓度和AQI指数以达到保护环境的目的，成为很多研究者重点关注的课题。

2. 因素筛选及对PM2.5影响程度分析

在这部分，我们将筛选出与PM2.5浓度变化有关的因素，并量化分析筛选出的因素对PM2.5浓度影响的程度。分析过程由以下步骤构成：

步骤一：数据预处理，并通过正态性校验判断是否适用于斯皮尔曼相关性分析。

步骤二：对比斯皮尔曼相关性分析及灰色关联分析结果，筛选出相关因素。

步骤三：通过随机森林回归对筛选出的因素进行排名，确定影响程度。

这部分的处理流程见图1。

2.1. 数据预处理

2.1.1. 数据问题描述

本文采集了2015年1月1日至2023年4月29日的8类污染物浓度数据：AQI、质量等级、PM10、O₃、SO₂、PM2.5、NO₂、CO，以及5类气象数据：降水量、平均气压、平均2分钟风速、平均气温、平均相对湿度。在原始数据中，大部分数据正常，但有些数据异常，有极少数数据为空值。

2.1.2. 预处理过程

本文首先对数据进行清洗 [1] 。去除异常值，对于缺失值，以三倍标准差的方法对数据进行填充。接着通过归一化处理将所有变量的值限于[0, 1]之间，此种方法可以将数值的绝对值转换为相对值，消除指标间的量纲影响，使各指标处于同一数量级，方便进行各指标间的综合对比评价。归一化结果见表1。

接着，对数据进行正态性检验，判断其是否适用于皮尔森分析法以及斯皮尔曼分析法。皮尔森相关性分析需满足变量存在正态分布。但经检验，所有大气参数及污染物结果全部呈现显著性(ρ > 0.05)，并不满足原假说，不服从正态分布。故本文采用斯皮尔曼相关系数分析法。

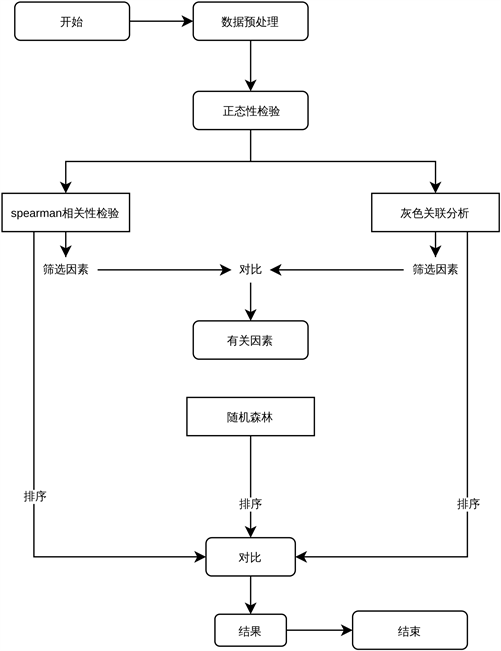
Figure 1. Flow chart of factor screening and its impact extent on PM2.5

图1. 因素筛选及对PM2.5影响程度流程图

Table 1. Normalized results

表1. 归一化结果

2.2. 模型建立

模型一. 斯皮尔曼相关系数分析

斯皮尔曼相关系数分析法被定义成等级变量之间的皮尔逊相关系数 [2] 。相关系数计算公式为：

$\rho =\frac{{\displaystyle {\sum }_i\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right)}}{\sqrt{{\displaystyle {\sum }_i{\left(x_i-\bar{x}\right)}^2}{\displaystyle {\sum }_i{\left(y_i-\bar{y}\right)}^2}}}$ (1)

但在实际应用中，变量与变量间的连结通常没有相关联系，基于此可通过更为简易的步骤计算相关系数。公式如下：

$1-\frac{6\sum d{i}^2}{n\left(n^2-1\right)}$ (2)

根据此模型，以大气参数及大气污染物为变量构建热力图判断其相关关系。

模型二. 灰色关联分析

灰色分析方法，是一种定量描述系统中因素对该系统发展态势的量化比较方法，其基本思想是通过序列几何曲线的相似程度来确定系统中因素对系统发展的联系程度。曲线相似程度越高，则系统中相应序列的关联度越大；相似程度越小，关联度也越小 [3] 。

经过分析可知，附件中各个变量序列的量纲不同，如果不对参数进行处理，直接分析，分析结果则会受到影响。因此在分析之前，需要进行去量纲处理。公式如下：

${\eta }_i\left(k\right)=\frac{{\min }_i{\min }_k\left|x_i\left(k\right)-x_0\left(k\right)\right|+\rho {\max }_i{\max }_k\left|x_i\left(k\right)+x_0\left(k\right)\right|}{\left|x_i\left(k\right)-x_0\left(k\right)\right|+\rho {\max }_i{\max }_k\left|x_i\left(k\right)-x_0\left(k\right)\right|}$ (3)

在上式中， $\left|x_i\left(k\right)-x_0\left(k\right)\right|$ 为 $x_0\left(k\right)$ 和 $x_i\left(k\right)$ 第k个点的绝对误差； ${\min }_i{\min }_k\left|x_i\left(k\right)-x_0\left(k\right)\right|$ 为两级最小差； $\rho$ 为分辨率， $0<\rho <1$ ，一般取 $\rho =0.5$ ； $\rho$ 越大，分辨率越小， $\rho$ 越小，分辨率越大。式中的 ${\min }_i{\min }_k$ ， ${\max }_i{\max }_k$ 分别为大气参数及污染物样本中的最小值与最大值。

计算关联度的公式如下：

$r_i=\frac{1}{n}{\displaystyle {\sum }_{k=1}^n{\eta }_i\left(k\right)}$ (4)

其中， $r_i$ 为 $x_i$ 对 $x_0$ 的关联度。

模型三. 随机森林回归

随机森林的算法步骤如下：

1) 从整合后的表格中抽取训练集。进行多轮抽取，从每次抽取的原始样本中使用Bootstrapin的方法抽取X个训练样本；

2) 使每个训练集都得到一个样本；

3) 针对回归问题，这里不作预测，而是通过算法得到特征重要性。

2.3. 模型求解

2.3.1. 因素筛选

方法一：采用斯皮尔曼相关系数分析法

以大气参数及大气污染物为变量构建热力图判断其间相关关系，斯皮尔曼相关性分析可以判断两变量间是否存在统计上的相关性，相关系数绝对值越大，说明两值其间的关系越紧密。基于此，本文通过热力图从宏观角度呈现大气参数、大气污染物与PM2.5间的关联程度。

其热力图结果如图2所示。

Figure 2. Heat map

图2. 热力图

根据相关系数绝对值的大小进行排序，可得到以下结果，见表2。

Table 2. Spearman correlation coefficient table

表2. 斯皮尔曼相关系数表

可得出与PM2.5浓度变化有关的因素有：PM10、CO、NO₂、SO₂以及气温。其中PM2.5与PM10、CO、NO₂、SO₂间具有强正相关，气温与PM2.5间存在强负相关。五个因素对PM2.5的影响排名如下：

PM10 > CO > NO₂ > SO₂ > 气温

方法二：采用灰色关联分析

通过对问题一的分析，可知需要建立一个PM2.5含量与气象参数和空气污染物浓度的相关模型。灰色关联分析是一种定量描述系统中因素对该系统发展态势的量化比较方法。它可以从几何角度出发，根据固定量列和对比数据列的相似程度来判断参考数据和比较数据间是否存在紧密联系 [2] 。

因此，选择灰色分析方法确定气象参数和空气污染物浓度对空气中PM2.5含量的影响程度。将 $\rho =0.5$ 代入公式，用MATLAB编程可计算得到PM2.5与PM10、CO、NO₂、SO₂、气温、风速、降水、O₃、湿度间的关联系数。部分结果见表3。

Table 3. Grey relational coefficient table

表3. 关联系数表

接着计算PM2.5与PM10、CO、NO₂、SO₂、气温、风速、降水、O₃、湿度间的关联度，结果见表4。

Table 4. Grey relation degree table

表4. 关联度表

显然可得与PM2.5浓度变化有关的因素有：PM10、CO、NO₂、SO₂、气温、风速。各个因素对PM2.5的影响排名如下：

PM10 > SO₂ > CO > 风速 > 气温 > NO₂

将方法一和方法二的结果综合对比可得：与PM2.5浓度变化有关的因素有：PM10、CO、NO₂、SO₂以及气温。

2.3.2. 对PM2.5影响程度分析

采用随机森林回归对各数据进行分析，此处运用随机森林模型并不是为了预测，而是通过算法找寻各因素对PM2.5的重要性程度。将结果与前两种方法进行对比，从而得到最为精准的结果。相较于从统计学出发斯皮尔曼相关性分析及从几何角度出发的灰色关联分析，通过随机森林回归可以从自身元素属性出发，避免决策单一化所造成的影响，可以有效提高结果准确度。结果见图3。

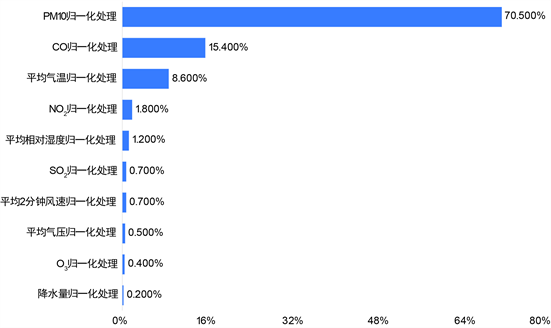
Figure 3. Ranking of importance of each factor on PM2.5

图3. 各因素对PM2.5特征重要性排行

由图3可得：PM10、CO、气温对PM2.5浓度有强影响。NO₂、SO₂对PM2.5浓度有较强影响。其他量影响较弱。将斯皮尔曼相关性分析、灰色关联性分析以及随机森林回归所得结果相对比，可得出以下结论：与PM2.5浓度变化有关的因素有：PM10、CO、NO₂、SO₂以及气温。其中PM10、CO、气温对PM2.5浓度有强影响。NO₂、SO₂对PM2.5浓度有较强影响。

3. 建立PM2.5浓度多步预测模型

3.1. 模型准备

在这部分，我们将构建PM2.5浓度多步预测模型，并通过用均方根误差(RMSE)对3步、5步、7步、12步预测效果进行评估。由以下步骤构成：

步骤一：数据预处理，将原始数据表格中年月日合并，将质量等级通过数字化呈现。

步骤二：设置步长，在Python中导入筛选因子，通过LSTM网络进行编译。

步骤三：通过均方根误差对结果进行检验，将检验结果可视化。

处理流程图如图4所示。

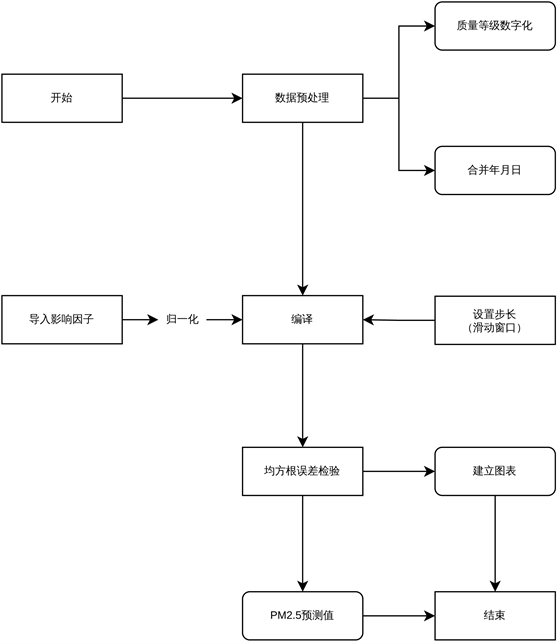
Figure 4. Flowchart of PM2.5 multi-step prediction model and its visualization

图4. PM2.5多步预测模型及可视化流程图

3.2. 模型建立

模型一. 多步预测模型

多步预测算法是一种基于时间序列数据的预测方法，可以预测多个未来时刻的数值。以下是一个简单的多步预测算法的伪代码。输入时间序列数据x，以及预测的步长n，将数据集分成训练集和测试集，使用训练集进行模型训练，得到预测模型对测试集进行预测，得到预测结果。

将测试结果中的最后 $n-1$ 个值作为输入数据，再次使用预测模型进行预测，得到下一个时刻的预测值 $y\_\left\{\text{test}+n\right\}$ 。将 $y\_\left\{\text{test}+n\right\}$ 加入预测结果 $y\_\text{pred}$ 中重复以上步骤，直到得到n个预测值再返回预测结果。在实现上述算法时，需要选择合适的模型和相关参数，如何选择模型和参数，需要根据具体的情况进行分析和实验。同时，还需要进行数据预处理、特征工程、模型训练等步骤才能实现一个高效的多步预测算法。简而言之，就是采用滑动窗口来进行预测。

以步长为3为例，具体的预测流程图见图5。

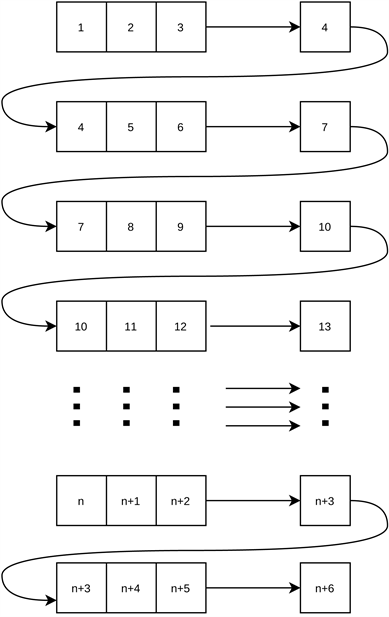
Figure 5. Step prediction flowchart (taking a step of three as an example)

图5. 步长预测流程图(以步长为三为例)

模型二. LSTM循环神经网络

传统的神经网络(BP神经网络)分为以下几个层次：输入层、隐含层和输出层。每一层中都有若干个神经元，每一层的神经元如同人脑中的突触般和下一层的神经元连接 [2] 。输入信号从输入层传入，经过隐含层的处理，进而从输出层输出。将输出层的数据和实际数据相比较，如果数据不相符，则进入反向传输，将误差分摊给隐含层的各个单元，从而建立一个稳定的模型。

但在前面的讨论中，PM2.5的值不仅与其他参数有关，还和PM2.5的历史数据有关，但BP神经网络不具有“记忆性”，况且利用多步预测，预测误差会随步长的累计而增大，而LSTM网络(长短时记忆神经网络)能消除对数据的长期依赖。因此采用LSTM建立模型和预测数据。

LSTM模型能够实现“记忆性”，又和普通的RNN模型不同，能够避免一般RNN模型对数据的长期依赖问题，而LSTM能够累计较远节点间的长期联系。因此选择LSTM模型对本问进行分析。LSTM通过四个独特的结构实现以上功能，分别为记忆单元、输入门、输出门和遗忘门，而且各个结构之间采用特殊的方式进行连接。

输入门：新数据(第2节所得的影响因素数据)经由输入门传入LSTM中，输入门经过数据处理，决定保存新数据中的某些数据，此后被处理过的数据被存入记忆单元。

遗忘门：控制记忆单元中要遗忘哪些数据，从而更新数据，解决对数据的长期依赖问题。

输出门：选择性输出记忆单元中的数据(PM2.5预测值)，决定数据是被直接输出还是传递至下一层LSTM。回到循环起点，开启下一轮循环。

可以用简单表示LSTM对数据的处理过程，见图6。

Figure 6. Flowchart of LSTM data processing

图6. LSTM数据处理流程图

检验方法：均方根误差检验

均方根误差与生活中常见的方差、标准差不同。其关系如图7所示。

均方误差的量纲通常与数据量纲不同，通常需要进行数据标准化，难以直观反映其间离散程度，故在均方误差上开二次方根，可得到均方根误差

$\text{RMSE}=\sqrt{\frac{1}{N}{{\displaystyle {\sum }_{t=1}^N\left({\text{Observed}}_t-{\text{Predicted}}_t\right)}}^2}$ (5)

式中的N指的是样本总量，而 $\text{Predicted}$ 及 $\text{Observed}$ 分别指代PM2.5的预测值与真实值。

Figure 7. Relationship diagram of variance, standard deviation, mean square error, standard error

图7. 方差、标准差、均方误差、标准误差关系图

均方误差通常用以衡量真实值与预测值间的误差。本文采用的是基于标准化数据的均方根误差，故均方根处在[0, 1]之间，越接近0，说明模型的预测能力越好。

总结：由于多步预测模型预测误差会随步长的累计而增大，而LSTM神经网络能消除多步预测模型的误差。故本文选择将两模型相合并，构建LSTM多步预测模型。

3.3. 模型求解

首先进行数据预处理，将年月日合并为日期。将质量等级(优、良)以数据[0, 6]来体现。

本文使用LSTM循环神经网络进行多步预测，并通过均方根误差，对结果进行检验。多步预测存在随步数的累计，预测结果越不精准的问题。而相较于其他神经网络，LSTM循环神经网络能够消除对累计数据的长期依赖，得到更为精准的预测结果 [4] 。

LSTM模型能够实现“记忆性”，又和普通的RNN模型不同，能够避免一般RNN模型对数据的长期依赖问题，因此成为分析本问题的首选。经过python中的Jupyter进行编译，其结果见表5~9。

Table 5. Table of RMSE for multi-step prediction (PM2.5)

表5. 多步预测均方根误差表(PM2.5)

Table 6. Three-step prediction results (PM2.5)

表6. 三步步长预测结果(PM2.5)

Table 7. Five-step prediction results (PM2.5)

表7. 五步步长预测结果(PM2.5)

Table 8. Seven-step prediction results (PM2.5)

表8. 七步步长预测结果(PM2.5)

Table 9. Twelve-step prediction results (PM2.5)

表9. 十二步步长预测结果(PM2.5)

接着，本文对预测数据进行了均方根检验，对模型的效果进行评估。经Python编译可视化结果如图8所示，由于长度问题，此处仅展示3步长的训练集与测试集的对比图，见图8，红线代表真实值，蓝线代表预测值。经过多次迭代后，训练集和测试集呈高度拟合。可见预测效果较为准确。

4. 构建AQI多步预测模型

4.1. 模型准备

我们的工作：构建AQI多步预测模型，并通过用均方根误差(RMSE)对3步、5步、7步、12步预测效果进行评估。并给出每天空气质量的预警等级颜色。由以下几个步骤构成：

步骤一：设置滑动步长，在Python中导入预测所需库，以LSTM神经循环网络进行编译。

步骤二：通过均方根误差对结果进行检验，将检验结果可视化。根据AQI值判断预警等级。

流程图如图9所示。

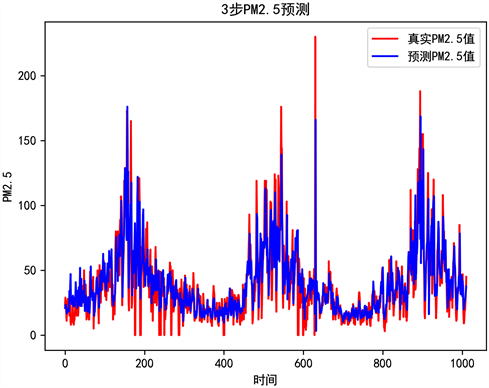
Figure 8. Visualization of test set and its predicted results (PM2.5)

图8. 测试集及其预测结果的可视化(PM2.5)

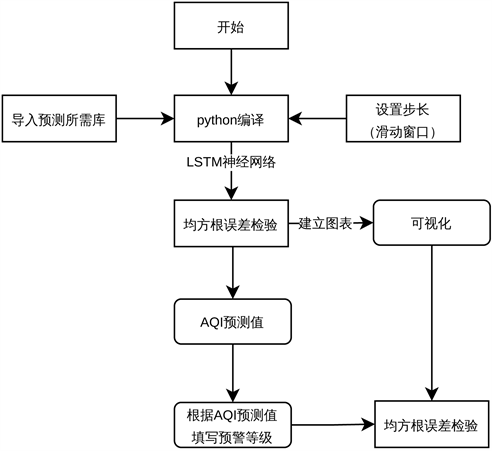
Figure 9. Flowchart of AQI multi-step prediction model and its visualization

图9. AQI多步预测模型及可视化流程图

4.2. 模型建立

均方根检验

在第3节中已有表述，此处不加赘述。

LSTM循环神经网络多步预测模型

根据前文建立的模型，我们构建LSTM循环神经网络多步预测模型。多步预测算法是一种基于时间序列数据的预测方法，可以预测多个未来时刻的数值。简而言之，就是采用滑动窗口来进行预测。

以步长为5举例，具体流程图见图10。

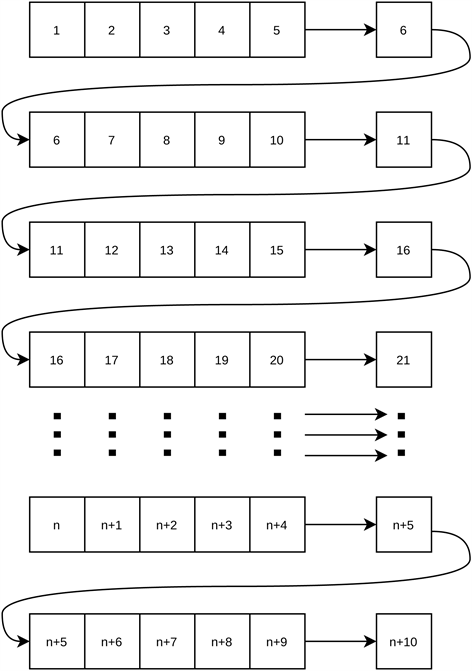
Figure 10. Step prediction flowchart (taking a step of five as an example)

图10. 步长预测流程图(以步长为五为例)

4.3. 模型求解

预测结果见表10~14。

Table 10. Table of RMSE for multi-step prediction (AQI)

表10. 多步预测均方根误差表(AQI)

Table 11. Three-step prediction results (AQI)

表11. 三步步长预测结果(AQI)

Table 12. Five-step prediction results (AQI)

表12. 五步步长预测结果(AQI)

Table 13. Seven-step prediction results (AQI)

表13. 七步步长预测结果(AQI)

Table 14. Twelve-step prediction results (AQI)

表14. 十二步步长预测结果(AQI)

预测等级可以通过Excel表格筛选或用python代码实现，本文采取了两种方法，取最优后得到结果，见表15。

Table 15. Summary table of the number of warning level colors

表15. 预警等级颜色次数汇总表

接着，本文对预测数据进行了均方根检验，对模型的效果进行评估。经Python编译可视化结果如图11。

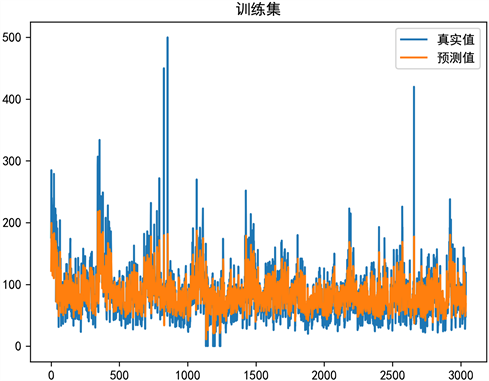
Figure 11. Visualization of test set and its predicted results (AQI)

图11. 测试集及其预测结果的可视化(AQI)

根据图11，蓝线代表测试集，橙线代表训练集。经过多次迭代后，训练集和测试集呈高度拟合。可见预测效果较为准确。

NOTES

^*通讯作者。