高斯公式在几个等式证明中的妙用——教学与科研相长的实践

Magical Effect of Gauss’s Law in Proving Some Identities—The Practice of Teaching and Research

摘要: 高斯公式是高等数学的一个重要知识点，在计算数学的科学研究中也有许多应用。本文给出了一个教学与科研相互促进的实例。在有限元基函数存在唯一性的科学研究中，提炼出一个多面体中带权有向面积等式，利用高斯公式给出简化的证明，并把该等式应用到高斯公式的教学中。

Abstract: Gauss’s formula is important in higher mathematics and has many applications in the scientific research of computational mathematics. This paper provides an example of the mutual promotion between the teaching and the scientific research. In the research of the existence and uniqueness of the finite element basis function, an equation related to a weighted oriented area in polyhedrons is proposed. A simplified proof is given by using Gauss’s law, and the equation is applied to the teaching of Gauss’s formula in the course of higher mathematics.

1. 引言

作为高校教师，教学与科研是两个本职工作，处理好它们之间的关系是非常重要的。众所周知，教学与科研不是相互制约、对立的关系，而是相辅相成、协同发展的关系 [1] 。通过教学，教师能够加深对知识的理解，促进其在科研中应用，解决科研上的问题。反过来，利用科研内容与授课知识点的联系，教师可以丰富教学素材，给学生讲述知识点的实际应用，反哺教学。

本文以高斯公式知识点为例，展示教学和科研是如何相辅相成的。本文首先对科研问题进行描述。在有限元理论中，基函数的存在唯一性是有限元方法成功的基础，通过简单推导，基函数是否存在唯一等价于一个不等式是否成立。用传统方法，该不等式的证明比较复杂，需要对四面体单元进行分类讨论。本文利用高斯公式给出了一个巧妙的证明，解决了科研问题。最后，本文通过对科研问题的解决过程进行总结，提炼出两个凸多面体上关于有向面积的恒等式，并把其当成教学素材，用于高等数学中高斯公式知识点的拓展。

2. 科研问题描述

设T为一个四面体， $L_T$ 为与T相交的一个平面，并把T分成 $T^{+}$ 和 $T^{-}$ 两部分， $n$ 为 $L_T$ 上指向 $T^{+}$ 的单位法向量，如图1所示，有两种相交情况。

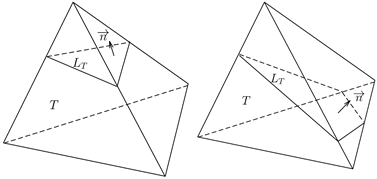
Figure 1. Two cases of the intersection of tetrahedrons and planes

图1. 四面体与平面相交的两种情况

在有限元方法中，T被称为单元。设 $P_1\left(D\right)$ 为定义在区域D上的所有线性函数的集合。传统线性有限元采用 $P_1\left(D\right)$ 作为形函数空间。但是对于界面问题，微分方程中存在间断的系数，传统的线性空间不能保证最优逼近性，因此有学者提出如下修正的形函数空间 [2] ：

$S\left(T\right)=\left\{\varphi :{\varphi |}_{T^{\pm }}\in P_1\left(T^{\pm }\right),{\left[\varphi \right]|}_{L_T}=0,{\left[\beta \nabla \varphi \cdot n\right]|}_{L_T}=0\right\},$

其中符号±表示+或者−， $\left[\varphi \right]={\varphi }^{+}-{\varphi }^{-}$ ， ${\varphi }^{\pm }={\varphi |}_{T^{\pm }}$ ， $\beta$ 为大于零的分片常数，即 ${\beta |}_{T^{\pm }}={\beta }^{\pm }>0$ 。

在有限元方法中，除了单元T和形函数空间 $S\left(T\right)$ ，还需要定义自由度，即 $S\left(T\right)$ 空间的对偶基 [3] 。设 $F_i$ 为单元T的第i个面， $i=1,2,3,4$ 。定义如下线性泛函作为自由度

$N_{i,T}\left(v\right)=\frac{1}{\left|F_i\right|}{\displaystyle {\iint }_{F_i}v\text{d}S},i=1,2,3,4,$

其中 $\left|F_i\right|$ 表示面 $F_i$ 的面积。有限元理论需要一个非常重要的结论： $S\left(T\right)$ 中的函数可以由 $N_{i,T}$ 唯一确定。具体可以写成如下定理：

定理1 对任意给定的常数 $b_i$ ，存在唯一的函数 $\varphi$ 满足

$\varphi \in S\left(T\right),N_{i,T}\left(\varphi \right)=b_i\forall i\in \left\{1,2,3,4\right\}$ 。

设 ${\lambda }_i$ 是面 $F_i$ 的传统有限元基函数，即 ${\lambda }_i$ 满足

${\lambda }_i\in P_1\left(T\right),\text{}\text{}\text{}{N}_{j,T}\left({\lambda }_i\right)={\delta }_{ij},$

其中 ${\delta }_{ij}=1$ 如果 $i=j$ ，否则 ${\delta }_{ij}=0$ 。给定函数v，定义其插值函数如下

${\Pi }_{T}v={\displaystyle \underset{i=1}{\overset{4}{\sum }}{N}_{i,T}\left(v\right){\lambda }_i}$ 。 (1)

在单元T上定义函数w满足

${w|}_{T^{-}}=w^{-}=0,{w|}_{T^{+}}=w^{+}\left(X\right)=\left(X-X_0\right)\cdot n,$ (2)

其中 $X_0$ 为平面 $L_T$ 上任意一点。由文献 [1] 可知，定理1等价于如下关于 $\alpha$ 的方程的解的存在唯一性

$\left(1+\left({\beta }^{-}/{\beta }^{+}-1\right)\nabla {\Pi }_{T}w\cdot n\right)\alpha =\left({\beta }^{-}/{\beta }^{+}-1\right){\displaystyle \underset{i=1}{\overset{4}{\sum }}{b}_i\nabla {\lambda }_i\cdot n}$ 。

由于 ${\beta }^{\pm }>0$ ，显然证明上述方程解的存在唯一性等价于证明如下不等式

$0\le \nabla {\Pi }_{T}w\cdot n\le 1$ 。 (3)

3. 基于高斯公式的巧妙证明

利用函数w和插值 ${\Pi }_T$ 的定义，不等式(3)可以转化为一个几何问题。根据平面 $L_T$ 与单元T相交的情况进行分类，如图1所示，可以给出不等式(3)的一个几何的证明，但是较为复杂。本文利用高斯公式给出一个简单的、无需分情况讨论的证明。首先回顾如下高斯公式 [4] [5] 。

${\displaystyle {\iiint }_{\Omega }\nabla \cdot F\text{d}V}={\displaystyle {\iint }_{\partial \Omega }F\cdot \nu \text{d}S},$ (4)

其中 $\Omega$ 为由光滑(或分段光滑)的封闭曲面所围成的区域， $\nu$ 为 $\Omega$ 的边的单位外法向量， $F$ 为定义在 $\Omega$ 上的多元向量函数且具有一阶连续偏导数。在物理上，高斯公式描述了在闭合曲面内的电荷分布与产生的电场之间的关系。在数学上，高斯公式可以看成牛顿莱布尼茨公式和格林公式在三维空间的推广，它反映了区域上三重积分和区域边界上曲面积分的本质联系。

实际上，巧妙地利用高斯公式可以证明如下更精细的结论，从而不等式(3)成立。

定理2对任意四面体T，任意与T相交的平面 $L_T$ ，都有

$\nabla {\Pi }_{T}w\cdot n=\frac{\left|T^{+}\right|}{\left|T\right|},$

其中 $\left|T^{+}\right|$ 和 $\left|T\right|$ 分别表示 $T^{+}$ 和 $T^{-}$ 的体积。

证明：首先，由(2)知

$\nabla \cdot {\left(wn\right)|}_{T^{+}}=\nabla \cdot \left(\left(X-X_0\right)\cdot nn\right)=1$ 。

接着，在高斯公式(4)中令 $\Omega =T^{+}$ ， $F=wn$ 得

${\displaystyle {\iint }_{\partial T^{+}}wn\cdot \nu \text{d}S}={\displaystyle {\iiint }_{T^{+}}\nabla \cdot \left(wn\right)\text{d}V}=\left|T^{+}\right|$ 。

由w的定义(2)可知w在平面 $L_T$ 上为零，则上述式子为

${\displaystyle \underset{i=1}{\overset{4}{\sum }}{\displaystyle {\iint }_{F_i\cap \partial T^{+}}wn\cdot \nu \text{d}S}}={\displaystyle {\iint }_{\partial T^{+}}wn\cdot \nu \text{d}S}=\left|T^{+}\right|$ 。 (5)

设 $l_i$ 为四面体T中面 $F_i$ 与对顶点的距离， ${\nu }_i$ 为面 $F_i$ 的单位外法向量，根据 ${\lambda }_i$ 的定义容易验证

$\nabla {\lambda }_i=\frac{4}{l_i}{\nu }_i$ 。 (6)

最后，由(1)，(5)，(6)可得

$\begin{array}{c}\nabla {\Pi }_{T}w\cdot n={\displaystyle \underset{i=1}{\overset{4}{\sum }}{N}_{i,T}\left(w\right)\nabla {\lambda }_i\cdot n}\\ ={\displaystyle \underset{i=1}{\overset{4}{\sum }}\frac{1}{\left|F_i\right|}\left({\displaystyle {\iint }_{F_i\cap \partial T^{+}}w\text{d}S}\right)\frac{4}{l_i}{\nu }_i\cdot n}\\ ={\displaystyle \underset{i=1}{\overset{4}{\sum }}\frac{1}{\left|T\right|}{\displaystyle {\iint }_{F_i\cap \partial T^{+}}w{\nu }_i\cdot n\text{d}S}}\\ =\frac{\left|T^{+}\right|}{\left|T\right|}\end{array}$ 。

证毕。

4. 在教学中的应用

在上述定理2的证明中，关键等式(5)是由高斯公式得到的。利用类似的思想，可以把公式(5)进行推广，提炼出如下两个多面体上的公式，用于高等数学中高斯公式的教学。

设 $\Omega$ 为有M个面的凸多面体， $F_i$ 为多面体的第i个面， $n_i$ 为面 $F_i$ 的单位外法向量， $\left|F_i\right|$ 为面 $F_i$ 的面积。称 $n_i\left|F_i\right|$ 为面 $F_i$ 的有向面积。

定理3 多面体的有向面积之和为零，即

${\displaystyle \underset{i=1}{\overset{M}{\sum }}{n}_i\left|F_i\right|}=0$ 。 (7)

证明：设 $e_1,e_2,e_3$ 为三个单位坐标向量，在高斯公式(4)中取 $F=e_j$ ，注意到 $\nabla \cdot e_j=0$ 得

${\displaystyle {\iint }_{\partial \Omega }{e}_j\cdot \nu \text{d}S}={\displaystyle {\iiint }_{\Omega }\nabla \cdot e_j\text{d}V}=0$ 。

由于凸多面体 $\Omega$ 有M个面，第i个面 $F_i$ 的单位外法向量为 $n_i$ ，面积为 $\left|F_i\right|$ ，上式左边可以写成

${\displaystyle {\iint }_{\partial \Omega }{e}_j\cdot \nu \text{d}S}={\displaystyle \underset{i=1}{\overset{M}{\sum }}{e}_j\cdot n_i\left|F_i\right|}$ 。

结合上述两个等式有

$\left({\displaystyle \underset{i=1}{\overset{M}{\sum }}{n}_i\left|F_i\right|}\right)\cdot e_j=0$ 。

最后，对j从1到3求和，利用 $e_1,e_2,e_3$ 为三个单位坐标向量可得

${\displaystyle \underset{i=1}{\overset{M}{\sum }}{n}_i\left|F_i\right|}={\displaystyle \underset{j=1}{\overset{3}{\sum }}\left({\displaystyle \underset{i=1}{\overset{M}{\sum }}{n}_i\left|F_i\right|}\right)\cdot e_j}{e}_j=0$ 。

证毕。

设L为一个有向平面，单位法向量为 $n_L$ 。平面L可以与多面体 $\Omega$ 相交，也可以不相交。定义函数 $w\left(X\right)$ 为点X到有向平面L的有向距离，即 $w\left(X\right)=\left(X-X_0\right)\cdot n_L$ 。令 $w_i=w\left(C_i\right)$ ，其中 $C_i$ 为面 $F_i$ 的重心。称 $n_i\left|F_i\right|w_i$ 为面 $F_i$ 的带权有向面积，则有如下多面体带权有向面积公式。

定理4 设 $\left|\Omega \right|$ 为 $\Omega$ 的体积，有

${\displaystyle \underset{i=1}{\overset{M}{\sum }}\left|F_i\right|w_i{n}_i}=\left|\Omega \right|n_L$ 。 (8)

证明：以 $n_L$ 方向为横坐标，建立新的坐标系。设新建坐标系的三个坐标向量为 $e_1,e_2,e_3$ ，其中 $e_1=n_L$ 。在高斯公式(4)中取 $F=w{e}_j$ 得

${\displaystyle {\iint }_{\partial \Omega }w{e}_j\cdot \nu \text{d}S}={\displaystyle {\iiint }_{\Omega }\nabla \cdot \left(w{e}_j\right)\text{d}V}$ 。 (9)

考虑到凸多面体 $\Omega$ 有M个面，第i个面 $F_i$ 的单位外法向量为 $n_i$ ，面积为 $\left|F_i\right|$ ， $w_i=w\left(C_i\right)$ ，其中 $C_i$ 为面 $F_i$ 的重心，与定理2的证明类似，(9)式左边可化简为

${\displaystyle {\iint }_{\partial \Omega }w{e}_j\cdot \nu \text{d}S}=\left({\displaystyle \underset{i=1}{\overset{M}{\sum }}\left|F_i\right|w_i{n}_i}\right)\cdot e_j$ 。 (10)

对于(9)式右边，注意到 $e_1,e_2,e_3$ 为三个坐标向量，其中 $e_1=n_L$ ，利用w的定义，有 $\nabla w=n_L$ ，且

$\nabla \cdot \left(w{e}_j\right)=\left(\nabla w\right)\cdot e_j+w\nabla \cdot e_j=n_L\cdot e_j=\{\begin{array}{l}1，j=1,\\ 0,j=2,3.\end{array}$

因此

${\displaystyle {\iiint }_{\Omega }\nabla \cdot \left(w{e}_j\right)\text{d}V}=\left|\Omega \right|n_L\cdot e_j$ 。 (11)

把(10)和(11)代入到(9)中得到

$\left({\displaystyle \underset{i=1}{\overset{M}{\sum }}\left|F_i\right|w_i{n}_i}\right)\cdot e_j=\left|\Omega \right|n_L\cdot e_j$ 。

最后，对j从1到3求和，利用 $e_1,e_2,e_3$ 为三个单位坐标向量可得

${\displaystyle \underset{i=1}{\overset{M}{\sum }}\left|F_i\right|w_i{n}_i}=\left|\Omega \right|n_L$ 。

证毕。

5. 总结

科研与教学是高校的两大重要职能，相辅相成、缺一不可。教学促进科研，科研反哺教学，本文通过高斯公式的应用实例说明教学和科研相辅相成。高斯公式是高等数学的一个重要知识点，往往课堂上给出的练习题没有实际应用或科研背景。本文通过高斯公式在科研中的妙用，提炼出了两个关于多面体上几何量的等式，并且给出了利用高斯公式的简单证明。这些等式当然可以通过几何关系得到证明，但是往往比较复杂。把这两个等式用作课堂讲授高斯公式的应用，不仅可以丰富教学素材，而且能够激发学生的学习兴趣，加深对高斯公式的理解。