1. 引言
在大型飞机的机身后体设计时,为了方便货物的装卸、武装伞兵的运输与投放、缩短起落架长度和避免飞机起降时机身尾部触地,往往将机身后体设计成有较大上翘角的后体形式,俗称“船尾形”。在巡航飞行时,上翘后体周围的绕流会出现横向流动,且后体处于全机边界层发展的下游,因此上翘后体的边界层容易出现漩涡分离流动,导致机身尾部出现较强的负压区,后体表面存在一定压力梯度,这是大飞机构型后体与传统平直后体绕流间的本质差异。
目前国内、外有关大型飞机后体流动机理的研究不够全面。国外仅在20世纪80年代开展了增压变雷诺数条件下的大型飞机后体压力分布研究 [1] 。而国内研究主要集中于大型飞机后体减阻方面。其中,黄涛等 [2] [3] 采用表面油流、烟线/激光片光显示和部件测力等试验方法,获得了随迎角由负至正增加,后体绕流的上分离–无分离–下分离的变化过程。张建军 [4] 采用CFD方法研究了侧鳍安装角、长度及厚度等几何参数对运输机上翘后体减阻效果的影响,给出了侧鳍几何参数的影响规律和设计原则。于彦泽等 [5] 研究了大型飞机机身后体的流动特征和机理,并采用涡流发生器对流动分离进行控制,讨论了不同参数对减阻效率的影响。程克明等 [6] 应用后体局部喷流主动控制技术对翼身组合体后体减阻进行了试验研究,结合尾流测压分析了喷气布局和喷气量对机身后体分离的控制效果,获得了良好的减阻效果。韩松梅等 [7] 通过测压试验结果,分析了迎角和起落架舱对大型飞机后体阻力的影响,结果表明大型飞机的机身后体流动分离是导致巡航阻力增加的一个重要因素。
以上工作在增进上翘、收缩后体绕流机理和后体参数设计等方面具有较大的促进意义,但目前的研究主要集中于优化减阻方面,对后体绕流及分离特性缺少系统研究;同时,船尾型后体底阻修正、支撑干扰影响等方面还没有深入分析,给试验设计和数据分析带来了较大难度。典型上翘、收缩型后体模型尾支撑实验示意图见图1所示。可以看出,模型后体绕流不仅受尾支杆的粘性近场干扰,支架机构堵塞的远场干扰也会对后体绕流产生影响;图2给出了俄罗斯T-128跨声速风洞中进行的运输机模型试验上翘收缩后体油流结果,可以看出明显的后体流动分离线。由于后体处于机身附面层发展的下游,其外形的上翘和收缩极易引起气流的分离,导致机身尾部出现较强的负压区,后体表面存在一定压力分布梯度,这是大飞机构型后体与传统后体绕流间的本质差异。该差异对试验结果的影响主要体现在模型底阻计算/修正,以及支架干扰对后体绕流影响两个方面。
目前高速风洞试验模型多采用尾支撑方式,由于支架系统的存在,带来后体绕流场畸变和底压分布的改变,直接影响对模型前阻、巡航效率等的准确预测,目前只能利用辅助支撑方式采用两步法试验测量支架干扰量,并在试验后进行统一修正。但是该试验方法仅考虑支架干扰对模型气动特性的宏观影响,忽略了底压变化以及模型后体流动特征等细节因素。同时,由于不同设备间支架、流场、洞壁、波反射等数据差异因素较多,无法准确评估支架干扰对数据准度影响的具体量级,增大了不同试验设备间数据相关性分析的难度,一定程度上限制了试验数据的大胆使用。
实际上,底压变化是支架干扰状态的直接反应,并前传影响模型后体表面压力分布。因此,底压与模型后体形状阻力之间必然存在一定关联。国外研究结果表明,战斗机类模型后体形状阻力与底压之间存在唯一的对应关系,在一定底压范围内这种关系基本上是线性的,见图3所示。利用该关系可以分析支架干扰对底部绕流特征的影响,并作为两步法的一种辅助手段评估和分析不同风洞设备和支架形式的阻力数据相关性。
大型军、民用运输机风洞试验技术是飞行器研制急需完善的试验技术之一,这类试验的主要特点是对阻力系数测量精度要求较高。因此,阻力系数是否准确,对飞机的航程与航时影响很大,关系到飞机使用过程费效比,直接影响飞行器研制进度和质量。本文系统研究了上翘、收缩型后体区域流动特性,通过数值模拟与试验方法,对比该类型后体与传统平直后体绕流的差异,分析后体表面及底部压力分布的均匀性,获得上翘、收缩型后体绕流及附面层分离特点,以及支撑系统对上翘、收缩型后体绕流的影响规律。通过该研究,可增进对大飞机上翘、收缩型后体绕流机理的理解,对不同试验设备间阻力相关性分析以及尾支撑干扰评估/修正具有一定的指导作用。
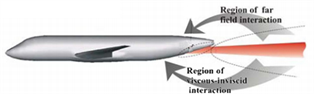
Figure 1. Experiment on the support of the rear body model after contraction and upwarping [8]
图1. 收缩上翘后体模型尾支撑实验示意图 [8]

 (a) (b)
(a) (b)
Figure 2. Flow visualization of T-128 wind tunnel rear body area [8]
图2. T-128风洞 [8] 后体区域表面流动显示
2. 后体绕流相关性分析
本文以运输机模型为研究对象,该模型采用上单翼、高平尾及翼吊发动机构型,机翼安装角3˚。模拟上翘角和收缩比影响时,为突出后体外形参数变化影响,计算翼身组合体状态;模拟支架远场干扰影响时,为与验证试验保持一致,计算了全机状态。
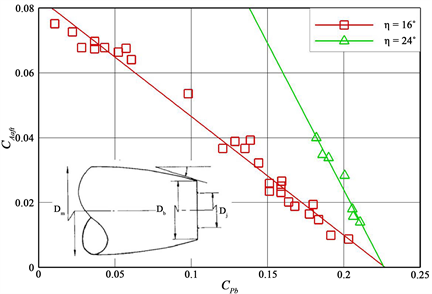
Figure 3. The relationship between the drag and the bottom pressure of the traditional model’s rear body shape
图3. 传统模型后体形状阻力–底压关系
2.1. 理论分析
2.1.1. 控制方程
本文采用守恒形式的N-S方程作为流畅控制方程,利用无量纲化处理可将方程改写为如下形式:
(1)
式中,V是Jacobi倒数,
是粘性开关参数(当
= 0时,(2.1)式为Euler方程,当
= 1时,(1)式为N-S方程);
是守恒变量,
、
、
是无粘对流通量,
、
、
是粘性扩散通量。方程(1)无量纲化时所引入的参数分别为密度
,速度
,压力P∞和能量
,温度
,长度L,时间
,粘性系数μ∞。
2.1.2. 离散方法
对(1)式采用隐式解法,得到一个非线性方程组,即:
(2)
将(2)式按时间方向展开,即以
为待求变量写成拟线性形式,舍去高阶项,并令
,于是可得下式:
(3)
以及
(4)
式中,A、B、C分别是对流通量
、
、
对
的Jacobi矩阵。令:
(5)
其中,
,这里
为矩阵A的特征值,同理定义
和
。
对式(3)左边时间项采用LU分解,右边的空间项采用Roe差分格式离散 [9] 。同时,为了加快收敛速度,采用多重网格技术 [10] ,计算时采用三重网格。
2.1.3. 湍流模型
本文采用k-ω SST(剪应力输运)湍流模型 [11] ,该模型是Menter在Wilcox提出的基本k-ω湍流模型的基础上,充分利用了k-ω湍流模型对逆压梯度比较敏感的特点而提出的,它能够模拟较大分离的流动;在远离附面层的流场中,采用k-ω湍流模型,克服k-ω模型对自由来流条件比较敏感的缺陷,提高了模型的稳定性。公式(6)至(8)为无量纲化的k-ω SST模型方程,方程中已经加入了可压缩修正,其具体形式为:
(6)
(7)
(8)
其中sk = 2.0,sw = 1.4,Ck1 = 1.0,Ck2 = 0.09,Cw1 = 0.555,Cw2 = 0.83,Cm = 0.09。
2.1.4. 计算网格
对CFD计算而言,网格质量直接影响CFD计算的精度,在计算方法已确定的情况下,网格的质量起着主要的作用。一个良好的计算网格,必须是贴体、正交、连续、光滑、在特定的区域内有足够的密度。
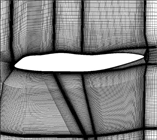
计算网格采用多块对接网格的形式,靠近物面区域生成附面层网格,法向第一层网格距离y+满足粘性模拟的要求。每一个子区域网格采用无限插值方法(TFI)生成,并根据需要进行椭圆方程优化。为减少计算量,仅模拟半模,网格量约1000万,其中物面网格及对称面网格如图4所示,不同后体外形及支撑机构位置的模型网格如图5所示。
 (a) (b)
(a) (b)
Figure 4. Calculation grid of upturned and contracted rear body model. (a) Surface grid; (b) Symmetric grid
图4. 上翘收缩型后体模型计算网格。(a) 表面网格;(b) 对称面网格
为减小网格差异导致的计算结果偏差,不同参数外形对应的计算网格通过基于弧长的无限插值方法生成,网格变形算法如下(y,z方向处理与x方向相同):
(9)
(10)
(11)
式中,
为物面法向的网格点序号。
采用这种方法对于后体区域外的网格点,变形前后位置保持不变,与其对应的空间网格点在变形过程中也保持不变,因此能够最大限度的使网格变形区域局限在模型后体范围内,减小参数变化前、后由于网格不同造成的数值计算误差。
2.2. 数值仿真
本文主要模拟后体收缩比和后体上翘角两个几何参数对后体阻力的影响规律;此外,为获得上翘、收缩型后体模型尾腔压力分布均匀性,分析支撑机构远场干扰对后体阻力的影响,开展了变底压数值模拟,计算了尾支撑机构不同位置时的后体绕流特性。主要计算内容见表1。
2.2.1. 上翘、收缩后体绕流特性分析
本文拟研究大型运输机模型上翘角和收缩比分别为β = 8˚,η = 0.21。图6和图7分别给出了该后体模型表面压力、马赫数分布,以及后体区域流线图,可以看出:

Table 1. Numerical calculation of the flow around an upward contracted rear body
表1. 上翘收缩型后体绕流数值计算
a) 随着轴向位置后移,后体上表面压力先减小后增大,而下表面压力系数由−0.11至−0.01单调递增,因此均存在较大的逆压梯度;
b) 在后体中前部,表面压力系数沿横向(周向,下同)由上表面0.03至下表面−0.07逐渐减小,存在较大的顺压梯度,导致流线向下偏移;
c) 在后体中后部,表面压力系数沿横向由下表面−0.01至上侧面−0.05逐渐减小,存在较大的逆压梯度,导致流线在后体下侧面汇集;
d) 在轴向逆压梯度作用下,上、下表面的气流在后体尾端均减速;在横向逆压梯度作用下,气流由上表面至下表面减速,尤其下表面出现了马赫数接近为0的区域;
由于逆压梯度的存在,后体下表面及侧面容易产生流动分离,并在尾迹区形成漩涡流向下游,造成尾部附近压力进一步降低,从而产生较大的压差阻力。
2.2.2. 收缩比对后体绕流影响
为分析后体收缩比对后体绕流的影响,固定后体上翘角β = 8˚,改变后体收缩比,计算了η = 0.14~0.49的后体绕流场,图8和图9给出了压力分布、马赫数分布及流线图,可以看出:
a) 随后体收缩比增大,后体尾部上、下表面的压力均减小。主要原因是后体收缩比增大致使尾部变钝、尾部截面积增大,气流到达尾部时因流管变细而速度加快,因而压力降低;
b) 由于后体中后部上、下表面的压力降低,从中后部到尾端区域上、下表面的轴向逆压梯度均增大。在粘性的作用下,上表面高马赫数区域减小、下表面低马赫数区域增大。
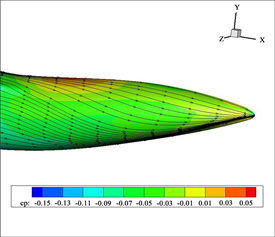
Figure 6. Surface pressure and streamline of upwarped and contracted rear body (η = 0.21, β = 8˚)
图6. 上翘收缩型后体表面压力和流线图(η = 0.21, β = 8˚)
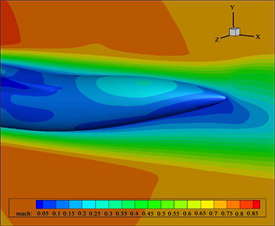
Figure 7. Cloud chart of Mach number on the surface of upward warping and contraction type after body (η = 0.21, β = 8˚)
图7. 上翘收缩型后体表面马赫数云图(η = 0.21, β = 8˚)
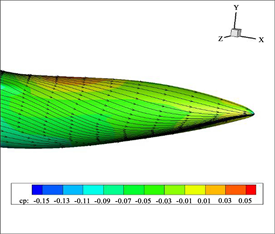
(a) η = 0.35, β = 8˚
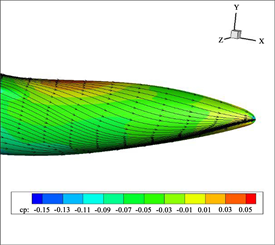
 (b) η = 0.42, β = 8˚ (c) η = 0.49, β = 8˚
(b) η = 0.42, β = 8˚ (c) η = 0.49, β = 8˚
 (d) η = 0.14, β = 8˚ (e) η = 0.28, β = 8˚
(d) η = 0.14, β = 8˚ (e) η = 0.28, β = 8˚
Figure 8. Surface pressure and streamline diagram of upturned shrinkage type after body (with different shrinkage ratios)
图8. 上翘收缩型后体表面压力和流线图(不同收缩比)

(a) η = 0.14, β = 8˚
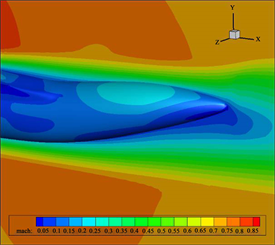
 (b) η = 0.28, β = 8˚ (c) η = 0.35, β = 8˚
(b) η = 0.28, β = 8˚ (c) η = 0.35, β = 8˚
 (c) η = 0.42, β = 8˚ (d) η = 0.49, β = 8˚
(c) η = 0.42, β = 8˚ (d) η = 0.49, β = 8˚
Figure 9. Cloud map of Mach number on the surface of upward shrinkage type after body (with different shrinkage ratios)
图9. 上翘收缩型后体表面马赫数云图(不同收缩比)
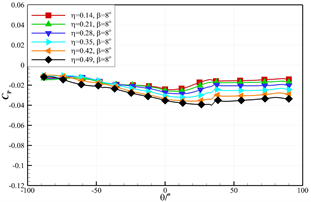
图10和图11给出了不同收缩比时模型后体表面沿横向和轴向的压力系数分布情况,其中横向截取位置为模型后体的起始截面和80% La截面,轴向截取位置为机身中轴线(机身后体轴向位置为823~1256 mm),可以看出:
a) 沿横向,在后体起始截面,从上表面至下表面压力系数近似线性减小,存在明显的顺压梯度,将导致流线向下表面偏移,且量值随着收缩比的增大而略增大,偏移强度增加;
b) 沿横向,在80% La截面,从侧面至下表面,压力系数增大,存在明显的逆压梯度,且量值随着收缩比的增大而略增大,将导致后体绕流出现分离流动;
c) 沿轴向,压力系数变化较为复杂,整体呈现压力升高的趋势,收缩比影响主要集中于后体后部区域,随着收缩比的增大,后体后部逆压梯度增大。
综上,随后体收缩比增大,后体压力降低,导致压差阻力增加;同时,后体面积增加,摩擦阻力也随之增大,因而总阻增加。
图12给出了零迎角状态下,模型升力系数、阻力系数和俯仰力矩系数随着收缩比的变化,可以看出,随后体收缩比由0.14增大至0.49,阻力系数由0.1689单调递增至0.1705,升力系数由0.2693至0.2676单调递减,并由于底部压力减小,产生一定抬头力矩,量值约为0.002。
 (a) (b)
(a) (b)
Figure 10. The distribution curve of the surface pressure coefficient of the upward shrinkage type afterbody along the transverse direction (with different shrinkage ratios) (a) Starting section; (b) 80% La cross-section
图10. 上翘收缩型后体表面压力系数沿横向的分布曲线(不同收缩比)。(a) 起始截面;(b) 80% La截面
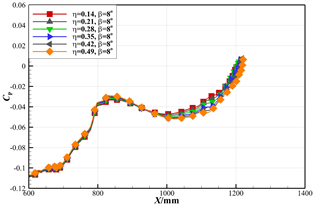
Figure 11. Distribution curve of surface pressure coefficient along the axial direction for upwarping shrinkage type after body (with different shrinkage ratios)
图11. 上翘收缩型后体表面压力系数沿轴向的分布曲线(不同收缩比)
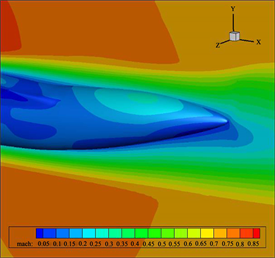
图13. 上翘收缩型后体表面压力和流线图(不同上翘角)
(d) η = 0.21, β = 4˚
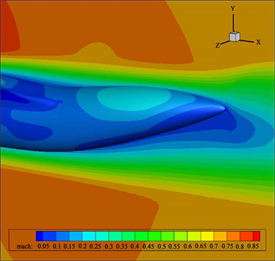
 (b) η = 0.21, β = 6˚ (c) η = 0.21, β = 10˚
(b) η = 0.21, β = 6˚ (c) η = 0.21, β = 10˚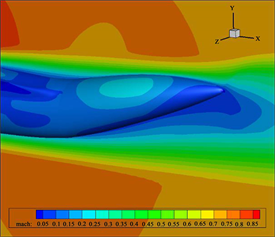
 (d) η = 0.21, β = 12˚ (e) η = 0.21, β = 14˚
(d) η = 0.21, β = 12˚ (e) η = 0.21, β = 14˚
Figure 14. Cloud map of Mach number on the surface of upward warping and contraction type rear body (different upward warping angles)
图14. 上翘收缩型后体表面马赫数云图(不同上翘角)
图15和图16给出了不同后体上翘角时模型后体表面沿横向和轴向的压力系数分布情况,可以看出:
c) 随着上翘角的增大,在后体起始截面上,沿横向从上表面至下表面顺压梯度单调递增,流线向下偏移速度加快;
d) 随着上翘角的增大,在80% La截面上,沿横向从下表面至上表面逆压梯度区域呈增大的整体趋势,将导致后体绕流的流动分离增强;
e) 压力系数沿轴向分布曲线形态与收缩比影响类似,但上翘角的影响区域略前移,集中于后体中、前部区域,随着上翘角的增大,后体中、后部的逆压梯度明显增大。
综上,随后体上翘角增大,后体横向逆压梯度增大,在粘性作用下流动分离加剧,故压差阻力增加;而且,后体浸润面积基本不变,摩擦阻力系数也基本不变。因而,随上翘角增加,总阻力增大。

 (a) (b)
(a) (b)
Figure 15. The distribution curve of surface pressure coefficient along the transverse direction of the upward contraction type after body (with different upward angles). (a) Starting section; (b) 80% La cross-section
图15. 上翘收缩型后体表面压力系数沿横向的分布曲线(不同上翘角)。(a) 起始截面;(b) 80% La截面
图17给出了零迎角状态下,模型升力系数、阻力系数和俯仰力矩系数随着上翘角的变化。可以看出,随后体上翘角由4˚增大至14˚,阻力系数整体趋势由0.1691至0.1714单调递增,升力系数由0.2714至0.2638单调递减,并产生一抬头力矩,量值约0.0071。
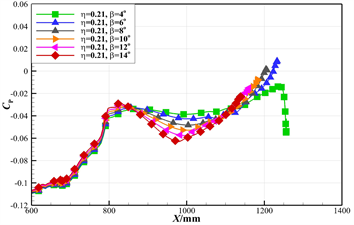
Figure 16. The distribution curve of surface pressure coefficient along the axial direction for upward shrinkage type afterbody (with different upward angles)
图16. 上翘收缩型后体表面压力系数沿轴向的分布曲线(不同上翘角)
 (a) CD0-η
(a) CD0-η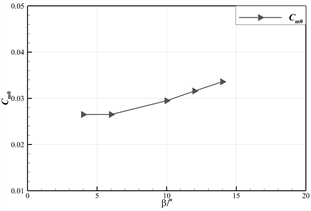
 (b) CL0-η (c) Cm0-η
(b) CL0-η (c) Cm0-η
Figure 17. Longitudinal aerodynamic force (moment) coefficient of the entire aircraft (with different upwarping angles)
图17. 全机纵向气动力(矩)系数(不同上翘角)
2.2.4. 支撑机构远场干扰影响
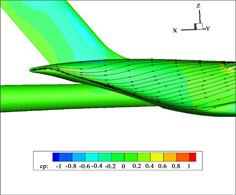
为分析支撑机构远场干扰对后体绕流特性的影响,固定后体上翘角β = 8˚和后体收缩比η = 0.21,计算了X = 1.86~3.72 (支撑机构前缘至模型质心的距离,以后体长度La进行无量纲化)的大飞机后体绕流场,图18给出了压力分布及流线图。可以看出,支撑机构对模型后体气流具有阻滞作用,随支撑机构位置前移,后体压力系数大于−0.2的区域面积增加,小于−0.2的区域面积减小,后体底部压力明显升高。因此,模型底压是支架远场干扰的直接反应,并前传影响模型后体表面压力分布。

(a) X = 1.86
 (b) X = 2.33 (c) X = 2.79
(b) X = 2.33 (c) X = 2.79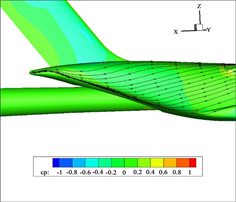
 (d) X = 3.26 (e) X = 3.72
(d) X = 3.26 (e) X = 3.72
Figure 18. Surface pressure and streamline diagram of upturned and contracted rear body (with different support positions)
图18. 上翘收缩型后体表面压力和流线图(不同支架位置)
2.2.5. 阻力–底压特性分析
战斗机类模型后体的尾支与真实的尾喷流存在可比拟的关系,而运输机类大飞机构型采用上翘收缩后体,尾支与尾喷流不存在这种关系,而且其高巡航效率设计对阻力测量准度的要求更高,使得底阻和尾支影响的准确修正更加重要。平直后体试验结果表明,模型底压随着支架干扰影响量的增大而增大,由于底压的变化,亚声速时底压的影响前传到模型后体表面,超声速时,高底压通过附面层前传到后体上,从而使流过后体的负压(相对于来流静压)气流更快恢复到来流静压值。因此,底压是支架远场干扰对模型后体阻力影响的直接反映,探索尾支底压与大飞机模型阻力特性之间的关联性,分析不同试验设备间阻力数据的相关性,对于提高试验数据质量和数据疑问排查工作具有明显的促进作用。
考虑到模型后体形状阻力单独测量的复杂性(需要进行测压试验或单独测量后体阻力),在忽略摩阻变化的假设前提下,本文将后体形状阻力问题转换为全机阻力问题,提出利用阻力特性-底压特性之间的关联来评估和分析不同设备间支架干扰远场影响的差异,假设条件如下:
(1) 忽略底压变化对前机身流动特性的影响
对于细长的机身模型,可以将前机身与后机身绕流问题分开考虑,即认为底压变化引起的阻力变化限制在机身后体范围内。由于运输机类模型机身较长,该简化是可行的;且在亚声速范围内,来流马赫数越高,底压变化的前传范围就越小,该假定就越接近实际流动情况。
(2) 忽略底压变化对模型表面摩擦阻力的影响
主要是忽略机身后体表面摩阻改变,认为其在试验中变底压范围内为常值。
在变底压过程中:
(12)
式中:
为扣除底阻影响的阻力,
为天平测得的模型总阻,
为底阻,
为模型前体形状阻力,
为后体形状阻力,
为表面摩阻。
由假设(1)和(2),可将形状阻力问题转换为全机阻力问题,进而把方程(12)改写为模型底压的函数形式:
(13)
方程右边底部实线标识项表示其为常数,不随底压变化;最后一项,底阻随底压变化为线性关系。因此,由方程(13)可知,底压对后体形状阻力的影响直接反应在扣除底阻后的模型前阻上,利用试验中天平测力修正后的结果即可获得底压–阻力特性关联曲线,进而评估由于不同支架干扰对应的不同模型底压对模型阻力特性的影响量级。
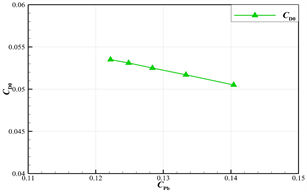
Figure 19. Relationship between total aircraft resistance and bottom pressure
图19. 全机阻力与底压关系
通过数值模拟和试验测试方法,在忽略摩阻变化的假设前提下,将后体形状阻力问题转换为全机阻力问题,给出了模型零升阻力系数CD0随模型底压系数CPb的变化曲线(如图19所示),验证了二者之间存在明显的线性关联。
3.2.6. 计算结果准确性检验
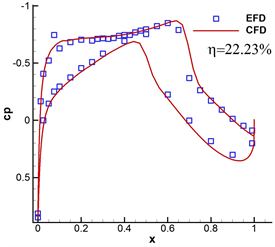
为验证数值计算方法的准确度,将计算结果与低温测压试验结果进行了对比。图20给出了α = 0˚、M = 0.76和M = 0.82条件下,距机身对称面22.23%展长的剖面压力系数的计算和试验对比结果。可以看出,在模拟范围内,计算结果与试验结果吻合较好,压力分布形态、吸力峰值、激波位置及后缘压力恢复系数等均吻合较好。说明本文所采用的计算方法是合适的,能够用于后续的研究工作。
 (a) M = 0.76, α = 0˚ (b) M = 0.82, α = 0˚
(a) M = 0.76, α = 0˚ (b) M = 0.82, α = 0˚
Figure 20. Comparison of pressure distribution between calculation and experimental results
图20. 计算与试验结果压力分布对比
3. 结论
本文通过计算大型飞机的上翘、收缩后体绕流,分析了后体收缩比、后体上翘角和支撑机构位置对后体绕流和气动特性的影响,检验了支架远场干扰对后体绕流特性的影响,获得了上翘收缩型后体尾腔内压力分布特性,主要结论如下:
a) 随后体收缩比增大,后体压力降低,导致压差阻力增加,且后体面积增加,摩擦阻力也随之增大,因而总阻增加;
b) 随后体上翘角增大,后体横向逆压梯度增大,在粘性作用下流动分离加剧,压差阻力增加,因而总阻增加;
c) 随着支撑机构位置后移,支撑机构堵塞前传影响降低,导致模型阻力系数增大;
上翘收缩型后体尾腔内流动受后体绕流影响,压力分布沿轴向波动较大,底压测量的位置应尽量伸入模型尾腔0.5倍支杆直径。
参考文献