NaF-AlF₃-LiF/KF熔盐体系的分子动力学势参数拟合研究

Study on Molecular Dynamics Potential Parameters of NaF-AlF₃-LiF/KF Molten Salt System

摘要: 由于我国北方地区铝土矿提取的氧化铝中含有钾、锂，导致我国铝电解质富含KF和LiF，使得电解质组分和物理化学特性发生变化。为此，本文采用对势拟合和力匹配相结合的方法，拟合得到了高精度的NaF-AlF₃-LiF/KF熔盐体系Born-Mayer-Huggins势参数，获得的势参数对微观粒子受力的拟合平均偏差方为0.0796，对密度和粘度等宏观性质计算偏差小于5%，表明其适用于NaF-AlF₃-LiF/KF基电解质微观结构和宏观性质的模拟计算研究。

Abstract: Due to the presence of potassium and lithium in the alumina extracted from bauxite in northern China, aluminum electrolytes in China are rich in KF and LiF, resulting in changes in electrolyte composition and physicochemical properties. In this paper, the Born-Mayer-Huggins potential parameters of the NaF-AlF₃-LiF/KF molten salt system were obtained by using the method of pairing potential fitting and force matching. The average deviation square of the obtained potential parameters for fitting the forces on microscopic particles is 0.0796, and the calculated deviation for macroscopic properties such as density and viscosity is less than 5%, indicating that it is suitable for the simulation of the microstructure and macroscopic properties of the NaF-AlF₃-LiF/ KF based electrolyte.

1. 引言

由于我国氧化铝原料含锂含钾的特性 [1] [2] [3] [4] ，导致在铝电解槽运行过程中易产生锂和钾的富集，形成NaF-AlF₃-LiF/KF型电解质，LiF和KF的富集会导致熔盐电解质熔点、密度以及导电率等诸多性质的变化，进而导致电解槽工况与电解质性质的不匹配，电流效率降低，因此，明晰铝电解质性质随锂、钾富集的变化对铝电解节能提质过程尤为重要。研究者们对含锂钾电解质做了大量的实验研究，结果表明锂盐的富集会导致电解质初级温度降低以及降低电解质密度 [5] - [12] ，有利于降低电解温度和促进熔盐与金属液的分离，但同时，氟化锂的富集同样也会导致氧化铝溶解度快速降低，导致异常生产工况 [13] [14] 。同样，氟化钾的富集也会导致电解质的初晶温度降低 [15] [16] [17] [18] ，更进一步的，研究者发现在电解质中适当掺入氟化钾盐能提高氧化铝在电解质中的溶解度，在K/(Na + K) = 10~30 wt.%区间时，氧化铝的溶解速度和溶解度将达到了峰值 [13] [19] 。对于富含锂、钾的铝电解质性质研究多集中于宏观性质的研究，对于其微观作用机理，人们研究较少，这是由于工况下的铝电解质为高温含氟熔盐，对精密检测设备的腐蚀性很强，试验成本代价昂贵，同时，熔盐电解质的微观离子基团结构对外界环境温度敏感，氟化物的易挥发特性导致实验过程中物料的组成特性易发生改变，导致实验的可重复性差，这些都限制了熔盐微观机理的研究发展。

随着计算机科学的不断发展，第一性原理计算和分子动力学模拟成为了实验检测研究之后的另一方法，第一性原理计算是基于量子力学理论，其实质是求解描述电子波函数的薛定谔方程，该方法求解精度高，但这对于一般的计算工作站来说，其计算量过于庞大，难以实现大体系长时间尺度的动力学模拟，故第一性原理多运用于原子基团的电子云分布、能级电子轨道和结合能等微观特性的研究；而分子动力学模拟以经典力学为基础，体系内原子之间相互作用关系用经验势参数描述，相比于第一性原理方法，分子动力学模拟极大地降低了原子运动方程的求解工作量，能实现大量原子体系在时间尺度ns和更高级别尺度的模拟计算。早期，国内中科院徐驰等人 [20] 采用Monte Carlo方法研究了Na₃AlF₆-Al₂O₃熔盐体系的离子结构，推测熔体中不仅含有[AlF₅]²⁻和[AlOF₃]²⁻等“单铝核”的离子基团，还含有F₃Al-O-AlF₃和F₃Al-F₂-AlF₃等“多铝核”的离子基团。D.K BELASHCHENKO等人 [21] 运用Born-Mayer势函数模型，研究了1283 K条件下的Na₃AlF₆-Al₂O₃体系的结构和电输运性质。发现在纯冰晶石体系中，Al-F平均离子配位数为6.4接近于6.0，并且随着Al₂O₃的加入，O²⁻逐渐取代了F⁻，形成Al-O-F基团；通过对外加电场下的离子迁移研究，发现Al³⁺表现为负的净电荷，这表明Al³⁺在F⁻的包裹下以基团形式存在。中南大学吕晓军等 [22] 基于第一性原理分子动力学，对1283 K条件下的Na₃AlF₆熔体的离子结构进行了研究，发现体系中熔盐保持短程有序，有Al-F离子团簇存在，其中[AlF₅]²⁻和[AlF₆]³⁻为主要团簇组成，[AlF₄]⁻含量很少；Al-F第一配位层平均配位数为5.45，团簇的F-Al-F键角主要位于87˚、124˚和171˚；体系中F离子主要以端氟形式存在，桥氟含量较少，为1%~2%，自由氟含量为26%左右。随后，他们进一步研究了CR = 2.2、LiF含量为1~9 wt.%的LiF-NaF-AlF₃体系的离子结构 [23] ，发现加入LiF会破坏了F离子桥，降低体系离子聚合度。从上述研究可知，对于熔盐铝电解质的研究多集中在Na₃AlF₆-Al₂O₃传统电解质体系，对富锂、钾电解质体系的研究较少，受限于体系势参数的缺乏，仅有少量的第一性原理计算研究，研究内容也多局限于离子基团结构变化研究，以小体系周期化的方式代替整个体系，难以完整描述熔盐电解质中离子基团的复杂作用关系，导致了电解质的粘度、电导率、密度等宏观研究与实际偏差较大。所以获得高精度的势能参数对于获得更加精准的NaF-AlF₃-LiF/KF熔盐体系内部基团结构和不同富锂、钾体系的宏观输运性质至关重要。熔盐体系中较为常用的势参数拟合方法为离子对势能曲线拟合 [24] [25] ，通过求两原子在不同间隔距离下的势能变化，并用经验方程对势能曲线进行拟合来获得两原子之间的势能参数，该方法获得的势参数描述的是两孤立原子之间的作用关系，其优点在于参数收敛性好，但获得的势参数对于体系微观结构以及性质的描述精准度很差。故本文结合第一性原理计算的高精度特性，通过在传统的对势拟合方程中加入离子受力匹配方程，该方法获得的势参数囊括了各离子所处环境的影响，提高了势参数对基团作用描述的精度。

2. 理论原理

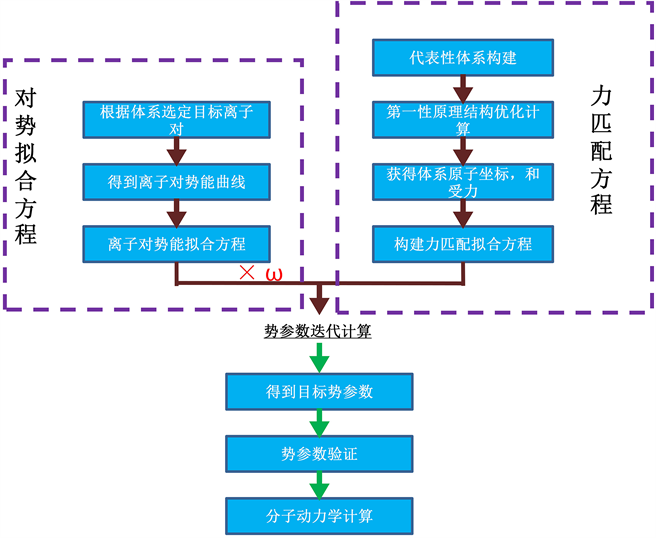
Figure 1. Potential parameter fitting flow chart

图1. 势参数拟合流程图

NaF-AlF₃-LiF/KF熔盐体系势参数拟合的基本原理流程如图1所示，拟合方程组由两部分组成，一部分是传统的对势拟合方程组，一部分是具备代表性的熔盐体系内离子的力匹配方程的搭建，对势拟合方程的精度差，但收敛性强，力匹配方程的描述精度高，但收敛性弱，通过一定的ω权重组合，能保证构建的方程组具备合适的精度和迭代收敛性，在实际的计算过程中发现ω取值为1即可保证迭代方程的收敛性和拟合参数的精度。拟合目标势函数选定为对熔盐离子电解质体系适应程度最高的经验势函数Born-Mayer-Huggins (B-M-H)，其总的势函数表达形式如式(1)和(2)所示：

$V^{tol}=V^{charge}+V^{BMH}$ (1)

$V_{tol}={\displaystyle {\sum }_{i<j}\frac{q_i{q}_j}{r_{ij}}}+{\displaystyle {\sum }_{i<j}\left[A_{ij}\exp \left(\frac{-r_{ij}}{{\rho }_{ij}}\right)-\frac{C_{ij}}{r_{ij}^6}+\frac{D_{ij}}{r_{ij}^8}\right]},r_{ij}<r_c$ (2)

式中第一项表示为离子的远程库伦作用势，用库伦公式计算，q_i和q_j为离子i和j所带的形式电荷量，r_ij为两离子相间距离，第二项为离子对之间的近程排斥作用项，后两项描述体系内偶极子相互作用以及偶极子和四极子相互作用。式中A_ij、ρ_ij、C_ij以及D_ij为离子i与j之间的对势作用描述参数，r_c为B-M-H作用势截断半径。当我们获得熔盐电解质中所有离子对的势参数，熔盐电解质中的相互作用力场便唯一确定，即可以实现熔盐电解质中各动力学模拟过程的研究。

力匹配方程的构建原理是通过对体系内原子的受力构建偏差方程，使得通过经验势参数计算得到的原子受力与第一性原理计算得到的原子受力分布倾向于一致。体系内的原子相互作用力公式可通过式(2)对r求偏导得到，如式(3)所示，受力偏差方程如式(4)所示：

$F_{classical}^i=-\frac{\partial V_{tol}}{\partial r_i}={\displaystyle {\sum }_{j=1,j\ne i}^N\left(-\frac{q_i{q}_j}{r_{ij}^2}-\frac{A_{ij}}{\rho }\exp \left(\frac{-r_{ij}}{\rho }\right)+\frac{6C_{ij}}{r_{ij}^7}-\frac{8D_{ij}}{r_{ij}^9}\right)}$ (3)

${\chi }_F^2=\frac{1}{N_c}{\displaystyle {\sum }_{j=1}^{N_c}\frac{1}{N_j}}{\displaystyle {\sum }_{j=1}^{N_j}\frac{{\left|F_{ab}^i-F_{classical}^i\right|}^2}{{\left|F_{ab}^i\right|}^2}}$ (4)

式中N_c为代表体系数目，N_j为代表体系j所含的原子总数， $F_{ab}^i$ 为原子i通过从头算结构优化计算得到的受力， $F_{classical}^i$ 为原子i通过势参数计算得到受力，在势参数迭代计算中是带有未知量(势参数)的一个表达式。 $\frac{{\left|F_{ab}^i-F_{classical}^i\right|}^2}{{\left|F_{ab}^i\right|}^2}$ 为原子i的受力均方差， ${\chi }_F^2$ 为方程组总的平均方差，一个力匹配方程组通常是由 ${\displaystyle {\sum }_{j=1}^{N_c}{N}_j}$ 个方程组成。

对势拟合方程的构建是基于拟合目标体系，得到所有存在的原子对种类，通过Gaussian算得线性分布的r_ij点处，原子i与原子j相互作用能V_Gaussian，通过式(2)我可得到距离为r_ij的原子i和j之间的作用能表达式为：

$V_{ij}=\frac{q_i{q}_j}{r_{ij}}+A_{ij}\exp \left(\frac{-r_{ij}}{{\rho }_{ij}}\right)-\frac{C_{ij}}{r_{ij}^6}+\frac{D_{ij}}{r_{ij}^8}$ (5)

由此可构建原子i与j的能量拟合方程

$E_{ij}^2={\displaystyle {\sum }_{n=1}^{N_r}\frac{{\left|V_{ij}-V_{Gaussian}\right|}^2}{{\left|V_{Gaussian}\right|}^2}}$ (6)

式中N_r为r_ij线性分布的取点数。 $E_{ij}^2$ 方程数与离子对数有关，对于一个有k个元素的体系，方程式有 $C_k^2+k$ 个。

本文最终构建的拟合方程组形式为：

$S^2={\chi }_F^2+{\displaystyle {\sum }_{m=1}^{C_k^2+k}{E}_{ij}^2}$ (7)

3. 拟合方程的构建与迭代计算

根据工业电解质常用电解质分子比以及锂、钾盐的富存状态，构建了4个锂电解质体系和3个钾电解质体系，共7个代表体系，其体系原子组成列于表1。

Table 1. Representative system composition of potential parameter fitting for NaF-AlF3-LiF/KF system

表1. NaF-AlF₃-LiF/KF体系势参数拟合的代表体系组成

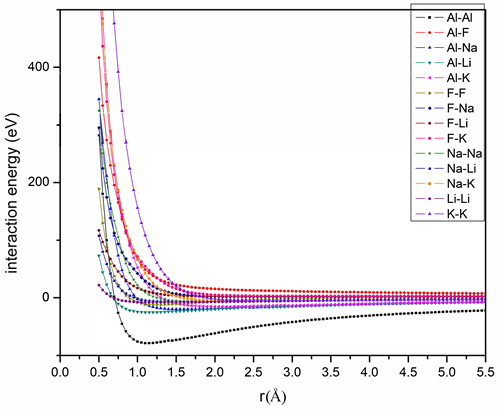
Figure 2. The ion pair potential energy curve of NaF-AlF₃-LiF/KF based electrolyte

图2. NaF-AlF₃-LiF/KF基电解质离子对势能曲线

NaF-AlF₃-LiF/KF电解质势参数拟合的力匹配方程组 ${\chi }_F^2$ 由(98 + 106 + 116 + 126 + 114 + 116 + 120)合计796个方程组合而成。对代表体系采用第一性原理计算进行结构优化，选择梯度关联函数(GGA)的PBE泛函。能量截断半径为598.7 eV，K点设置为1 × 1 × 1精度，自洽迭代(SCF)收敛精度为1.0e⁻⁶ eV/atom，结构能量收敛精度为1.0e⁻⁵ eV/atom，受力收敛精度为0.03 eV/Å。由于代表体系较小，为了保证体系结构变化趋势尽可能的明显，在结构优化过程中允许对体系的晶胞常数进行优化。利用第一性原理计算精度高的特点，对小体系进行结构优化，并以优化后的结果构建力匹配方程，能使拟合势参数，对相应体系的结构和某些性质的描述达到近似第一性计算的精度，同时充分发挥分子动力学方法对于大熔盐体系计算效率高的特点。该体系内总共有五种类型的单离子，合计14个离子对方程，分别为离子对Al-Al、Al-F、Al-Na、Al-Li、Al-K、F-F、F-Na、F-Li、F-K、Na-Na、Na-Li、Na-K、Li-Li、K-K。其拟合的能量曲线如图2所示。

同样，根据式(6)搭建对势拟合方程，最终获得拟合方程组式(7)，通过Lsqnonlin算法对方程组S²不断迭代求解获得极小值参数，即为NaF-AlF₃-LiF/KF基电解质的B-M-H势参数。求解得到的B-M-H势参数如表2所示：

Table 2. B-M-H potential parameters of NaF-AlF3-LiF/KF based electrolyte

表2. NaF-AlF₃-LiF/KF基电解质的B-M-H势参数

4. 势参数计算验证

4.1. 力匹配验证

将获得的B-M-H势函数参数代入公式(3)可以获得第一性原理计算优化体系内每个离子的受力 $F_{classical}^i$ 的具体数值，通过以 $F_{classical}^i$ 在x轴方向的偏量为横坐标，以第一性原理计算的 $F_{ab}^i$ 在x方向的力矢量为纵坐标可以得到图3。

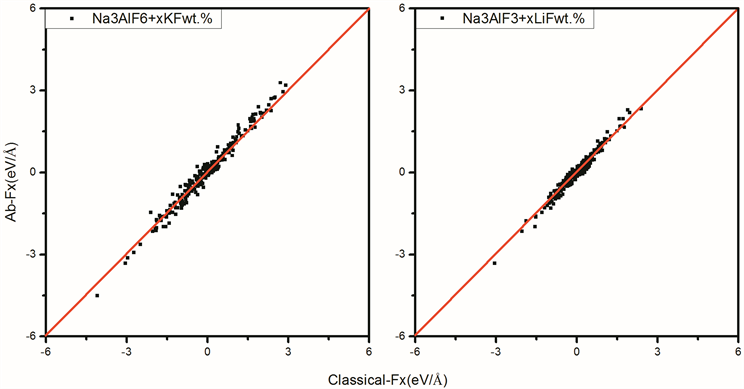
Figure 3. Verification of force matching between classical molecular dynamics potential parameter calculation and first principles calculation

图3. 经典分子动力学势参数计算结果与第一性原理计算结果的力匹配验证

从图可以看出， $F_{classical}^i$ 与 $F_{ab}^i$ 大致上沿 $y=x$ 直线分布，表明经典分子动力学计算结果与第一性原理计算结果具有极佳的匹配度，通过式(4)我们可以得到拟合体系的平均偏差平方 ${\chi }_F^2$ 以及每个离子的标准

相对偏差平方 $\frac{{\left|F_{ab}^i-F_{classical}^i\right|}^2}{{\left|F_{ab}^i\right|}^2}$ ，将离子偏差作概率分布如图4所示。

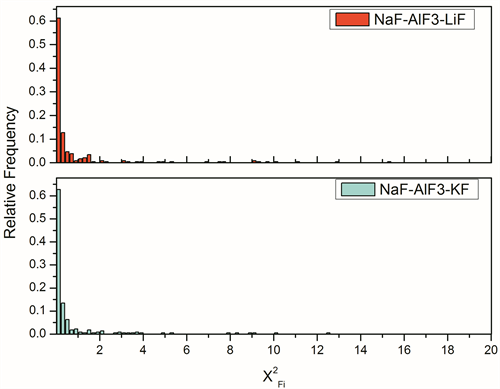
Figure 4. Probability distribution histogram of ion deviation square in NaF-AlF₃-LiF/KF system

图4. NaF-AlF₃-LiF/KF体系中离子偏差方的概率分布柱状图

NaF-AlF₃-LiF体系中偏差方小于0.1的占比59%以上，偏差方小于1的占比超过78%，其中偏差方小于0.01的占比达到36.2%。NaF-AlF₃-KF体系拟合效果要更佳，偏差方小于0.1的占比超过62.7%，其中偏差方小于1的占比超过86%，其中偏差方小于0.01的占比达到43.9%。由于拟合体系的受力平均都在0.7 eV/Å以下，有的甚至小于0.0005 eV/Å，所以细小的绝对误差也会造成巨大的偏差方的产生，通过图3不难发现有部分原子的力匹配偏差极大，实际上有部分能达到15330和10893的偏差方，通过对相应离子的索引，发现这些离子具备相同的特征，离子所处位置在x轴方向具备一定的对称性，使得离子受到的合力极小，两离子在x方向的分力分别为0.002326 eV/m和−0.0004 eV/m，，在拟合过程中较小的绝对误差都会导致巨大的相对误差产生，通过对这一类原子造成的误差进行扣除，体系的平均偏差方为0.0796，其拟合精度比Salanne等人 [26] 对LiF-NaF-KF体系的力匹配势参数拟合精度0.0879更高。

4.2. 宏观性质验证

采用拟合得到的势参数，对已有的实验研究体系进行相同条件下的分子动力学模拟计算，比较实验测量值与模拟计算值的偏差，以此来验证势参数的可靠性，实验性质采用测量可靠度较高的密度，同时也选取了少量的粘度测量结果进行对比，实验结果列于表3。

Table 3. Comparison between calculated results and experimental results of macroscopic properties of NaF-AlF3-LiF/KF system

表3. NaF-AlF₃-LiF/KF体系宏观性质计算结果与实验结果对比

表中为模拟计算值，括号内为实验参考值，a [26] [27] ，b [28] 上标表示不同研究者的实验成果，从上表不难发现，针对已有的实验研究体系，本文拟合的参数无论是对体系密度还是体系的粘度，模拟结果与实验测量结果的偏差在5%以内，密度的偏差更是在3%以内，表明拟合得到的势参数能很好的描述NaF-AlF₃-LiF/KF基电解质的微观结构和宏观性质，且无论是高锂、钾盐含量还是低锂、钾盐含量电解质，都具有极高的匹配精度。

5. 结论

针对现有的铝电解质含锂、钾盐的特性以及NaF-AlF₃-LiF/KF基电解质微观机理不明，动力学模拟计算势函数精度低的现状，采用力匹配原理与对势拟合相结合的方法，对NaF-AlF₃-LiF/KF电解质体系的B-M-H势参数进行了拟合研究，拟合结果表明：

1) 通过力匹配验证，该势参数能够很好地描述原计算体系，拟合的平均偏差方为0.0796，表明其适用于NaF-AlF₃-LiF/KF基电解质微观结构的研究，同时得到的势参数对于富钾熔盐电解质微观结构的描述精准度更高。

2) 通过宏观性质验证，该势参数的宏观性质计算与已有实验研究数据偏差极小，普遍在5%以下，表明其适用于NaF-AlF₃-LiF/KF基电解质宏观性质的研究。

致谢

本论文由2022年八师石河子市重大科技计划−100 KA三层电解提纯5 N高纯铝技术开发项目资助，项目编号：2022ZD02。