1. 引言
计算机科学的快速发展使得当代科学研究能够很容易地收集到海量数据集,特别是在金融领域。而金融领域指数型衍生品创新在金融危机中表现突出,被大多数投资者和机构所采用,根据指数来选择股票成为投资者重点关注之一,因此,如何用部分股票来追踪目标指数就成为是否采用指数法进行投资的关键所在,指数跟踪技术的目的是使投资者获得较高利益。股票指数追踪研究的内容是通过权重的优化再配置来寻找使得该组合指数的追踪误差最小部分股票,实现组合收益与指数涨跌基本一致,此研究具有高精度、低交易成本、且能保证追踪组合的高流动性,具有重要的意义 [1] 。
本文在解决股票指数追踪问题时,第一步先采用绝对约束估计和弹性约束估计对原始变量进行降维,再根据误差分析结果,选择使得指数追踪误差更小的解释变量作为指数追踪的研究对象,第二步用最小二乘估计建立经验回归方程,保证系数的估计是无偏的,有更小的残差平方和,寻找部分股票构成的最优的追踪组合。
2. 材料与方法
2.1. 数据采集
本文数据来源于金融choice,选取上证50成分股收盘价数据。表1展示上证50包含的50家上市公司,如伊利股份、中国电信、山西汾酒、贵州茅台、招商银行、中信证券等。

Table 1. List of stocks in the Shanghai 50 Index
表1. 上证50指数成分股列表
该数据集一共有243个样本,包括50个解释变量和1个响应变量(上证50指数),部分数据展示如下表,可以看到宝钢股份和中国石化的收盘价几乎在5元以下,而兆易创新的收盘价则超过100元,这里说明了不同企业的收盘价会存在较大差异,需要在建模前要对数据进行标准化。
2.2. 统计分析方法
在金融大数据统计分析中,首要的问题就是变量的选择问题,由于变量的影响、数据收集的成本和分析的时效不同,并不总是需要尽可能多的收集全部的变量,且证券市场中很多变量是相互依存的,这时也没有必要将高度关联的变量都考虑进来。变量选择较为常用的方法有以下3种:逐步回归法、绝对约束估计、弹性约束估计。
逐步回归法的基本思想是将变量逐个引入模型,每引入一个解释变量后都要进行F检验,并对已经选入的预测变量逐个进行t检验,当原来引入的预测变量由于后面预测变量的引入变得不再显著时,则将其删除。以确保每次引入新的变量之前回归方程中只包含显著性变量。这是一个反复的过程,直到既没有显著的预测变量选入回归方程,也没有不显著的预测变量从回归方程中剔除为止。以保证最后所得到的预测变量集是最优的。
绝对约束估计(Lasso)通过构造一个惩罚函数得到一个较为精炼的模型,使得它压缩一些回归系数,即强制系数绝对值之和小于某个固定值 [2] ;同时设定一些回归系数为零。因此保留了子集收缩的优点,是一种处理具有复共线性数据的有偏估计。Lasso就是在普通的线性回归模型的残差平方和后加入1范数惩罚项,具体数学表达式如下,
(1)
s值控制了收缩情况。s值越大,变量收缩较小;s值越小,变量收缩越大,部分变量系数变成0,所以Lasso具有重要的稀疏性质。Lasso的复杂程度由λ来控制,λ越大对变量较多的线性模型的惩罚力度就越大,从而最终获得一个变量较少的模型,故一个合适λ值对建立指数追踪模型尤为重要,在后续的建模中将使用交叉验证选取最优的λ值。
弹性约束估计(Elastic Net)结合了岭回归和Lasso的正则化方法通过两个参数λ1和λ2来控制惩罚项的大小 [3] ,具体数学表达式定义如下:
(2)
当λ1 = 0时,弹性约束估计就是岭回归,当λ2 = 0时,弹性约束估计就是绝对约束估计,因此,弹性约束估计同时具有绝对约束估计和岭估计的特点 [4] 。
普通的线性回归模型要求满足高斯马尔可夫条件 [5] ,即误差项同方差、0均值、且不相关,而对线性回归模型中回归系数或误差方法进行估计,通常采用最小二乘估计,因为其估计出来的参数具有优良的性质,设多元线性回归方程如下:
(3)
普通最小二乘法拟合线性模型,本质上是要寻找使得残差平方和达到最小的系数估计,这时所估计的系数满足无偏性、有效性,即最小二乘估计的方差最小 [6] 。
3. 描述分析及多重共线性检验
3.1. 描述分析性统计分析

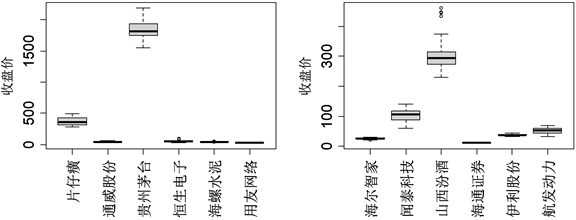
Figure 1. Analysis of box chart of closing price of some enterprises
图1. 部分企业收盘价箱线图分析
从图1可以发现,招商银行、万华化学、贵州茅台、山西汾酒4个企业相比于同组的其它公司,其收盘价均值、最大值、最小值、第1四分位数、第3四分位数的表现都遥遥领先,其中贵州茅台的收盘价最高,均值超过1500元。从上图的第1幅箱线图可看到中国石化收盘价整体上略高于宝钢股份,但总体收盘价水平差不多,中信证券相比于三一重工收盘价均值略高,但三一重工收盘价浮动较大,中信证券更加稳定;第2幅箱线图中,北方稀土、复星医药、恒瑞医药3个企业差别不大,其中北方稀土和复星医药存在较多异常值,同组内上汽集团收盘价最低,均值在20左右;第3幅箱线图可以发现通威股份、恒生电子、海螺水泥、用友网络这四个企业收盘价表现大致相同;第4幅箱线图中,除闻泰科技和山西汾酒外,其它企业收盘价这段时间内收盘价一直低于100,最差的是海通证券,且发现山西汾酒数据存在较多异常值。对于上述分析中存在异常值的变量都借助R软件中的cooks.distance()函数计算其库克距离,再结合现实情况采取剔除、修正或保留等措施。
3.2. 多重共线性检验
为了说明哪几个自变量之间有一定的多重共线性的关系存在,接下来使用方差扩大因子法来诊断多重共线性 [7] ,表2给出了49个企业所对应的方差膨胀因子。没有列在表格内的韦尔股份的方差膨胀因子为122.59,一般认为回归方程的多重共线性的存在就是由方差膨胀因子超过10的这几个变量引起的 [8] ,但是针对本例,没有低于10的方差膨胀因子,最低的是隆基绿能的14.71,通过查看方差膨胀因子较大的企业与其它公司的相关系数,发现这些企业会与多数的企业具有较强的相关性,而方差膨胀因子较小的隆基绿能等企业就出现与以上情况相反的情况,故重点关注方差膨胀因子较大的特征变量,如宝钢股份(37.01)、三一重工(89.90)、长城汽车(73.3)、中国电信(88.124)、等,可以结合lasso和Elastic Net降维的结果综合考虑采用剔除这些变量等方法来解决多重共线性问题。

Table 2. Variance inflation factor of Shanghai 50 enterprises
表2. 上证50企业的方差膨胀因子情况
4. 上证50股票指数追踪实证分析
4.1. 绝对约束估计
选取上证50成分股收盘价数据对Lasso和Elastic Net的变量选择方法在指数跟踪方面的应用效果进行详细分析。本文将样本数据集划分为训练集(2/3)和测试集(1/3):共有161个拟合样本,80个预测样本。利用绝对约束估计得到了回归方程的系数估计,其中宝钢股份、北方稀土、恒力石化、恒生电子、三峡能源、中国神华、工商银行、长城汽车、中国建筑、华泰证券、中国电信、中国石油、中远海控、华友钴业等14个变量系数为0,即Lasso方法剔除了14个解释变量,还剩余36个解释变量。
从图2可以发现,在训练集上证50指数跟踪图中,星号代表拟合值,实线代表真实值,可看出实际走势和36只成分股的跟踪走势基本重合,偏离程度较小,除拐点外,两条曲线在一定程度上几乎重合,说明该时间段内目标指数的跟踪效果良好。而对于指数跟踪效果,不能只看模型在训练集中的表现,还需要用测试集数据进行验证,从预测残差图看到1~65号样本预测残差在0附近波动,最高在20附近,而从65号样本之后预测残差呈直线上升趋势,最高超过60,结合测试集指数跟踪情况,发现40号样本之后,预测指数和实际指数趋势虽然相同,但是基本没有重合,而是在上下波动,故Lasso回归(绝对约束估计)在预测集取得良好的指数跟踪效果,而在测试集的表现不尽如人意。
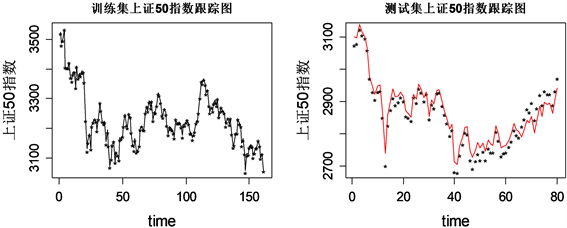
Figure 2. Absolute constraint estimation residuals and visualization of tracking results
图2. 绝对约束估计残差及跟踪结果可视化
4.2. 弹性约束估计
利用弹性约束估计得到了回归方程的系数估计,其中宝钢股份、北方稀土、恒力石化、恒生电子、三峡能源、中国神华、工商银行、中国人寿、长城汽车、中国建筑、中国电信、中国石油、中远海控、华友钴业等14个变量系数为0,Elastic Net方法(弹性约束估计)剔除的变量多数与Lasso方法相同,唯一不同的是Elastic Net方法剔除了中国人寿,而Lasso方法删除了华泰证券。
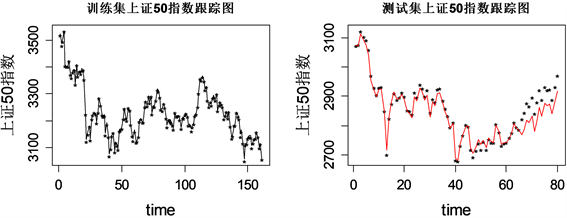
Figure 3. Residual estimation with elastic constraints and visualization of tracking results
图3. 弹性约束估计残差及跟踪结果可视化
图3中对于训练集指数跟踪效果,Elastic Net方法预测残差图和Lasso方法看上去大致相同,都是从65号样本之后预测残差呈直线上升趋势,最高超过60,而从Elastic Net测试集上证50指数跟踪图可以看到,65号样本之前实际走势和预测走势基本重合,比Lasso方法追踪效果好,而从65号样本之后,预测误差很大,基本脱离真实值。
4.3. 基于弹性网降维的两步估计回归模型
前面部分的分析中,Elastic Net方法为我们选择了包括中国石化、中信证券、三一重工等36个解释变量,使用这36个解释变量和响应变量上证50指数建立一般的线性回归模型,通过最小二乘估计获得拟合模型,使得系数估计具有无偏性。
其估计残差及跟踪结果展示如图4所示,训练集的表现效果与单独使用Elastic Net和Lasso方法看起来相差不大,但是可以发现基于弹性网降维的两步估计模型(后简称两步估计)明显的改善了预测集的上证50指数追踪效果,预测残差总的在−10到10之间波动,65号样本之后的残差不再呈直线上升趋势,最大值也从之前的60几降低到10几。从测试集上证50指数跟踪图可以看到预测曲线和真实曲线基本重合,取得良好的指数跟踪效果。
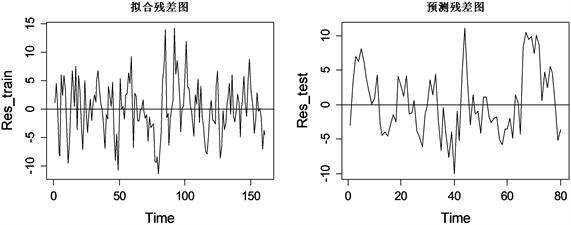
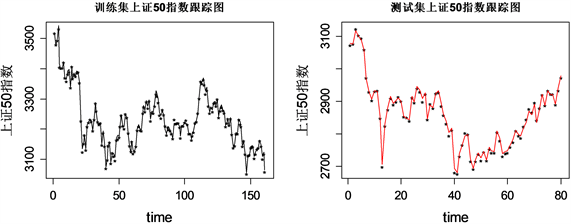
Figure 4. Residual estimation with elastic constraints and visualization of tracking results
图4. 基于弹性网降维的两步估计残差及跟踪结果可视化
表3给出了弹性网降维的两步估计回归模型的误差分析,对比分析在逐步回归删除不显著变量前后模型于四个评价指标的上的表现 [9] 。训练集上两者变现差不多,而在测试集上,两步估计 + 逐步回归模型(30个自变量)略优于两步估计模型(36个自变量),且考虑作为基金公司,需要用最少的变量达到对指数的跟踪,从而实现股票与股指期货的对冲,故两步估计 + 逐步回归模型(TSERS)将作为我们上证50指数追踪的最终模型。

Table 3. Variance inflation factor of Shanghai 50 enterprises
表3. 上证50企业的方差膨胀因子情况
最终TSERS模型解释变量及其系数估计如下,此时回归系数是无偏的,且所有的变量均显著,模型的R-squared为0.9994,Adjusted R-squared为0.9994,p-value为2.2e−16,远远小于0.05,说明模型是显著的,且具有较好的拟合效果。下表4给出了最终的参数估计结果。

Table 4. Two-step estimation of dimensionality reduction of elastic network + stepwise regression model coefficient
表4. 弹性网降维的两步估计 + 逐步回归模型系数
为了更好地对比各个模型的效果,表5给出了四个模型的误差对比分析。
可以发现两步估计 + 逐步回归在4个指数追踪评价指标上的表现都一致的好,进一步说明该方法的优势。

Table 5. Comparative analysis of errors on four regression model test sets
表5. 四个回归模型测试集上的误差对比分析
5. 总结
股票指数追踪作为投资组合策略,能帮助投资者从证券市场获得超出预期的收益,在一定程度上降低投资风险,受到很多投资者青睐。本文以上证50指数及其成分股为研究对象,构建了基于弹性网降维的两步估计回归指数追踪模型。第一步采用弹性约束估计对原始成分股进行降维,第二步建立最小二乘估计经验回归方程,并且采用逐步回归方法来剔除不显著变量。其中还包括了对原始数据的异常值检验和变量间的多重共线性检验。通过指数追踪实证研究验证明,本文提出的模型在拟合性、预测性、误差最小性上都取得较好的结果,实现了较优的指数追踪效果,并使得投资组合的稀疏性达到最优,一定程度上降低了投资者的投资成本,具有一定的实际指导意义。