1. 引言
区间图(Interval Graph)是对应到数轴上满足特定关系、以一组区间为表现形式的相交图,称数轴上的区间为区间表示。若各区间长度一致,则称该区间图为单位区间图 [1] 。区间图在电路设计、物流调度与网络管理问题等方面有重要运用,是图论研究中的热点图类之一 [2] 。
控制函数旨在搜索查找出一个顶点集S,使得图中该集合外的顶点至少与S中的一个顶点相邻。罗马控制函数(Roman Domination Function, RDF)将图的顶点集赋值为0、1、2,要求函数值为0的顶点至少要拥有一个函数值为2的邻居。在此基础上,total-罗马控制函数(Total Roman Domination Function, TRDF)增加了条件,即要求搜索查找出的顶点集S的诱导子图中没有孤立点存在 [3] 。
1999年,Stewart [4] 在《Scientific American》杂志上发表的《Defend the Roman Empire》一文中首次提出了包围罗马帝国的军队调控策略,通过调动各城市内驻扎的军队,保护罗马帝国免受外界多次攻击。自此,罗马控制问题引起广泛关注。2003年,Michael及其团队在《Discrete Mathematics》上接连发表了《Defending the Roman Empire from multiple attacks》《Defending the Roman Empire-A new strategy》等文章,研究保护罗马帝国的新型防守策略,推动罗马控制问题走向研究热潮 [5] [6] 。随时间发展,罗马控制问题得到变形,如双罗马控制、完全罗马控制和total罗马控制。total-罗马控制作为衍生问题之一,要求制定出特殊方案使得以下两个条件成立:① 在某座城市没有军队驻守的情况下,该城市的某一座邻居城市中一定驻守着两支军队,可使在危难来临前,邻居城市中的军队可分派一支前往保护该城市;② 拥有军队驻守的城市之间存在联系,即没有孤立的城市存在。2008年,Mathieu Liedloff等人研究了罗马控制在图类上的运用,表明区间图上的罗马控制数可用在线性时间内计算出来,证明存在多项式时间算法可用于计算无AT-图以及带有d-octopus的图的罗马支配数 [7] 。在2009年前,罗马控制函数及其变形如弱罗马控制函数等问题经常处于热点研究状态 [8] [9] [10] [11] 。2013年,Liu和Chang介绍了图中total-罗马控制函数的概念 [12] 。在 [13] [14] 中,作者对total-罗马控制函数继续进行研究,推动了total-罗马控制及罗马控制问题的发展。2018年,杨洪等人研究了区间图上的罗马控制,设计出求解罗马控制数的动态规划算法 [15] 。同年,Jafar Anjadi等人研究了total-罗马控制上的Nordhaus-Gaddum不等式,将total-罗马控制数与补图、图中所有顶点之间的最小度联系起来,得出系列不等式关系 [16] 。2020年,Jafar Amjadi继续给出total-罗马控制方面的钻研成果,开始了关于total-罗马控制在图中细分数的研究 [17] 。经常与其他控制相结合,total-罗马控制的研究前途广泛,未来还可应用于不同图类。
如下图1所示,本文主要从两个方面来刻画total-罗马控制函数。首先在文章第2节,介绍区间图、total-罗马控制函数等基础知识;在第3节介绍total-罗马对,以此为第一方面对total-罗马控制函数所具备的性质进行刻画,证明相关定理的正确性;在第4节介绍区间图中关于团、路径、团与团的并、团与路径的并等图的total-罗马控制数,是本文在第二方面的刻画;第5节,总结全文。
2. 符号和预备知识
图(Graph)是由点、边以及各点之间存在的邻接关系所构成的三元组,用符号表示为
,其中
和
分别表示图G的顶点集和边集。若一个图拥有n个顶点,则称
为图的阶数,称该图为n-顶点图。区间图(Interval Graph)是对应到数轴上满足特定相交关系的图类,图中顶点与数轴上的区间一一对应。本文研究简单、无向且有限的区间图,即图中不含重边与圈、边上没有方向以及图的边集与顶点集中元素有限。
在图G中,对于顶点集中任意两个顶点u、v,若
,则称u、v互为邻居,也称此两点满足邻接关系。用
表示任意顶点u的开邻域、
表示其对应闭邻域。对于任意两个满足
的顶点集A、B,用
表示从集合B中删去A中所有元素,也写作
。若A是单元素集,不妨设
,则
,也即是
。对于任意顶点集
,其诱导子图
保留了S中所有点及各点在图G中所对应的边,也是一个图。
团(Clique)是指任意两个顶点之间都存在邻接关系的图。路径(Path)具有顺序,设n阶路径
,称第一个顶点
、最后一个顶点
分别为P的左、右端点,其中
。设存在任意正整数s、t使得
与
是两条顶点集互不相交的路径,这两条路径按照不同顺序首尾相连后,分别可以表示为两条新路径,即
、
。特别地,若路径是单元素路径,不妨设
,则两条路径相加可表示为
、
。
定义1 区间图与区间表示一一对应,区间表示由区间构成。区间具有长度,分别记区间
的左、右端点值为
和
。给定一个图
,若存在一组区间
满足关系:对任意顶点
,
当且仅当
,则称该图G为区间图,称I为G的区间表示 [18] 。
在区间表示I上,对于任意区间
、
满足
,记
表示区间
先于区间
出现且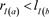 。对于区间
与顶点集S满足
,记
表示区间
。对于区间
与顶点集S满足
,记
表示区间
先于集合S中任意区间出现,即
。
定义2 n-顶点区间图G的右端点序列
是指各顶点在区间表示I中按右端点按序列重新排序的结果,满足:对任意顶点i、j,
当且仅当
。注意,若无特别说明,本文中的区间排序统一为右端点排序。如下图2所示,左图为7-顶点区间图,右图为对顶点进行右端点排序后的结果,其中,
。
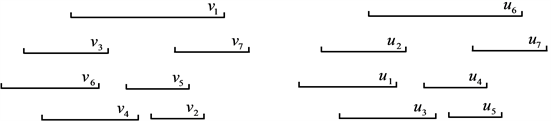
Figure 2. Example: an interval graph (left) and the graph sorted by right endpoint sequence (right)
图2. 示例:区间图(左)和该图按右端点序列排序后的图(右)
定义3 给定任意图G,如果集合
满足对任意顶点
都存在另一个顶点
使得
,那么称S是G的一个控制集。G的控制数用
表示,其中
是G所有控制集中阶数最小的集合。在控制集基础上,total-控制函数(Total Domination Function, TDF)要求由控制集诱导的图中无孤立点存在,其控制数用
表示;罗马控制函数(Roman Domination Function, RDF)是函数
,满足:对G中任意函数值
的顶点u,至少存在一个邻居v使得函数值
。罗马控制函数也可表示为
,其中
。该图G中的罗马控制数表示为罗马控制函数的权值最小值,符号记作
。
定义4 给定图G,total-罗马控制函数(Total Roman Domination Function, TRDF)是函数
,满足条件:(1) 对G中任意函数值
的顶点u,至少存在一个邻居v使得函数值
;(2) 由控制集
且
诱导的子图没有孤立点存在。total-罗马控制数表示为
,称
为图G的total-罗马对,简写为
形式 [4] 。如下图3所示,在7阶区间图G中,存在total-罗马控制函数
,此时控制数
,控制集
中无孤立点存在,total-罗马对表现为
。
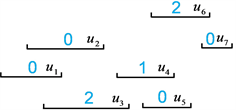
Figure 3. An interval graph G with a total-Roman Domination Function
图3. 区间图G及其total-罗马控制函数
3. 基于Total-罗马对的定理研究
定义5 已知
是区间图的区间表示,对任意
,记
表示区间
完全包含于
,写作
,也称
完全包含
[18] 。
定理1 若
是区间图G的total-罗马对,那么
中的区间不能完全包含于
中的另一个区间,即由
诱导的子图是严格区间图。
证明 反证法,设存在两个顶点
使得区间
完全包含于
。结合区间图按右端点序列进行排序可知
,因此
成立,故
也是区间图G的一个total-罗马对,与
是G的total-罗马对矛盾。因此,
中的区间不能被完全包含于另外一个区间中。
定理2 若
是n阶区间图G的total-罗马对,那么
中不会包含
阶团。
证明 反证法。当
时,设
是一个3阶团。由定理1可知,
中的区间不存在包含与被包含的关系,故设
中3个区间的端点值在数轴上满足
,因此
,这表明区间
能控制的区间(包含
在内)都可被区间
与
控制,即
也是该区间图G的一个total-罗马对,与已知条件矛盾,故
中不含3阶团。
同理,当
时,设
是
阶团。由定理1可设个顶点对应的区间端点值满足关系
。使用数学归纳法进行演算,可得到关系
,这表明区间
与
能控制
中其余区间控制的所有区间(包含这些区间在内),即
也是该区间图G的一个total-罗马对,与已知条件矛盾,故中不含阶团。
综上,
中不含
阶团。
定理3 如果
是n阶区间图G的total-罗马对,那么由
诱导的各连通分量表现为路径,且每条路径阶数大于等于2。
证明 由于区间图G没有孤立点,。由定理1可知,由
诱导的每个连通分量都是一个严格区间图,因此,这些严格区间图不含爪形图
。结合定理4.2可知,由
诱导的各连通分量表现为路径。若存在一条路径的阶数为1,那么这条路径只包含1个顶点,与total-罗马控制关于控制集的定义矛盾,故定理3成立。
另,若这些严格区间图是弦图(弦图中长度超过3的每个圈中都包含一条弦),那么图中一定包含的最小圈为
,因
是3阶团,与定理2矛盾,故这些严格区间图不含弦图。
4. 区间图total-罗马控制数
4.1. 区间图中关于团的total-罗马控制数
定理4 任意n阶区间图G按右端点序列排序后满足以下:
若G为团且
,那么
。
若
为团且
,那么
。
若G为
阶团,任意添加区间
后,
。
证明 (1) 设区间右端点序列为
。若G为团,那么任意两个区间之间都存在相邻关系,即对任意区间
总存在另一个区间
使得
,其中
。因此,上述所有区间均满足
。同理可知,G的区间相互包含,不妨设存在
是图G的一个total-罗马对,因此
。
(2) 若
为团,结合(1)中可知在3阶团
中,对任意
知区间
都满足
,设
是图
的一个total-罗马对。
图G无孤立点,故一定存在顶点
使得
,要么
,顶点
可被顶点
直接控制,要么
,故
,顶点
也可被顶点
控制。因此,
不仅是图
的一个total-罗马对,同时也是图G的一个total-罗马对,
。
(3) 已知G为
阶团,若
,添加的区间
右端点值最大,可能出现的情况共有n种,即
,其中
。当
时,
与
相交,此时
为
阶团,由前述定理4中(2)可知,
,此时的total-罗马对是
。为更好将新添加区间
纳入考虑,根据题意可知
也是满足情况的total-罗马对。当
时,考虑
与其他区间相交。因G为
阶团,故将
赋值为2后,可控制G内其他所有区间,因此
中区间赋值为0,另将
赋值为1,故存在
是图
的一个total-罗马对,此时,
。综上,无论新添加区间
所处何种位置,都存在
是图
的一个total-罗马对,因此total-罗马控制数
。
定理5 若区间图G中两个不相交的团G1、G2分别与G中区间
相交,那么
。
证明 设区间图G按右端点序列排序,s阶团G1、t阶团G2区间不相交,分别对应区间表示
、
,存在一个区间
分别与两个团相交,设
、
。添加新区间
且与
具有相同相交关系。根据定理4,对于图
,存在
是一个total-罗马对。同理,对于图
,存在
是
的一个total-罗马对,因此,total-罗马控制数满足关系
。由于
与
具有相同的控制性,因此删去
后,
的存在仍能保持图中的控制性,故
,并且在
时,存在
是图
的一个total-罗马对。
如下图4所示,10阶区间图G按右端点序列排序,G1、G2分别是4阶、5阶团且区间不相交,其中
、
、
,根据上述定理,取
赋值为1,任取顶点
与顶点
赋值为2,此时,total-罗马控制数满足关系
。
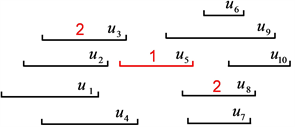
Figure 4. Example: an interval graph with 10 intervals G
图4. 示例:10阶区间图G
4.2. 区间图中关于团和路径的Total-罗马控制数
引理1 n阶图G是圈或路径
[17] 。
设f为对应的total-罗马控制函数,顶点集
,通过引理1可以得到
。在后文引用引理1时,不妨设
,即图G中的顶点全部赋值为1。
定理6 若区间图G中s阶团H与G中t阶路径P的端点相交,那么
,其中正整数
、
。
证明由已知设区间图G的区间表示为I、顶点集
、
。若团H中的区间只与路径P的一个端点区间相交,那么易知这个端点为
。添加新区间
且与
具有相同的相交关系。对于图
,由定理4可知存在
使得
是图
的一个total-罗马对,此时
。对于路径P,由引理1可知
。结合定理5证明中的思想易知
,故
,并且在
时,存在
是图
的一个total-罗马对。
若H中的区间与P的包含端点区间
在内的多个区间相交,那么存在正整数
使得
,即区间
的右端点值大于路径P中前k个区间的左端点值,因此将区间
赋值为2后,路径P中存在k个区间被
控制,为了保证图
的total性质,只能将P中
个区间赋值为0,故图
的total-罗马控制数
。特别地,这种控制函数的寻找方法同样适用于团H中的区间只与路径P的一个端点区间相交的情况。
如下图5所示,区间图G阶数为8,
、
、
、
、
,
,取等时,将H中右端点值最大的区间赋值为2、将路径P中第k个及之后的区间赋值为1,所得控制集即为该图G的total-罗马控制集。

Figure 5. Example: an interval graph with 8 intervals
图5. 示例:8阶区间图G
定理7 区间图G中两个团G1、G2相交,团的并图满足
。
证明 设区间图G的区间表示为I。G有G1、G2两个满足区间相交关系的团,分别对应区间表示I1、I2,团内按右端点序列排序,故对任意正整数
,设
、
。易知
是I1中右端点值最大的区间,且可控制I1中其他所有区间。由于两个团中区间存在相交关系,不妨设
,即
,其中
。
若
,即
,故区间
与I1中的每个区间都相交,
可控制I1中所有区间。由定理4可知G2中存在
使得
,不妨设
,
,其中
。那么
也即是图
的total-罗马对,此时
。如下图6左所示,3-团与4-团对应的区间表示I1、I2已用不同颜色进行标注。同理,若
,即区间
与I2中的每个区间都相交,那么存在
使得
。如下图6右所示,在保证区间相交关系不变的情况下,可适当伸缩区间长度。
在其他情况下,易知
、
分别可以控制I1、I2中其他所有区间,由于
,故存在
是图
的一个total-罗马对,此时total-罗马控制数
。
特别地,若
中任意两个区间都相交,那么
是一个
阶团,故
。
综上,定理得证。结合定理7与定理5还可推广到满足区间相交的k个团,即若区间图G的k个团依次满足区间相交,那么图G1、G2的并的total-罗马控制数
。
5. 结论
基于区间图,本文首先介绍了total-罗马对,主要研究了团和路径中的total-罗马控制函数性质以及团与团的并、团与路径的并等结合问题中的total-罗马控制数,在证明过程中多用反证法和数学归纳法,以示例辅助理解,在3阶及以上区间图中证明了以下几个主要结论:
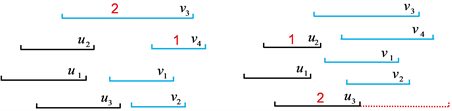
Figure 6. Example: two interval representations I1、I2 in interval graph G
图6. 示例:区间图G中两个区间表示I1、I2
1) 若
是n阶区间图G的total-罗马对,那么
中不会包含阶团;
2) 任意n阶团的total-罗马控制数为3;
3) 任意n阶团添加任意顶点后的total-罗马控制数为3;
4) 相交团的并的total-罗马控制数不超过4;
在后续研究中,还可探讨以团和路径为基础的区间图的total-罗马控制函数性质、多个团及多条路径的并的total-罗马控制数等问题。
基金项目
重庆市研究生科研创新项目(CYS23687:罗马控制及变形问题研究)。
参考文献