1. 引言
为提高其飞行稳定性,战术武器通常采用绕轴转动的飞行模式,如导弹、火箭弹、炮弹等。旋转弹丸在飞行时会产生额外的侧向力—马格努斯力 [1] [2] 。由此产生的马格努斯力矩将影响弹丸的航向动稳定性,降低命中精度,因此对旋转马格努斯力矩的准确预测就成了弹箭研发的重要课题。然而,作用在弹箭上的气动力与气矩,却因为低速尾迹流动与强制旋转运动的耦合等复杂的气动干扰而呈现出极强的非线性、非定常状态,这对准确预测弹箭的气动特性提出了挑战。
20世纪80年代以来,国内外开展了大量的飞行器旋转空气动力学效应研究工作。Vishal [3] 使用雷诺平均Navier-Stokes方程(RANS)计算Finner滚动阻尼和马格努斯力矩,但轴向力相对于试验值 [4] 偏高。DeSpirio [5] 对M910旋转弹丸绕流场进行了数值模拟,结果显示在亚声速和跨声速下流速,采用RANS/LES混合的DES湍流模型,计算的马格努斯力矩更好地与实验值相符合。RANS/LES混合法的基本思想是:采用RANS高效可靠地模拟高频小尺度运动占主导地位的近壁区域,同时利用LES精确计算低频率大尺度运动占优的非定常分离流动区域。RANS-LES混合法是在当前有限计算资源条件下处理高雷诺数大分离流动的合理选择,已广泛应用于模拟多种流动类型 [6] [7] [8] [9] 。
国内学者,主要采用工程方法或者求解RANS方程计算旋转弹丸的马格努斯力矩 [10] - [16] 。陈东阳等 [17] 选用剪切应力输运(shear stress transfer, SST)湍流模型,通过求解RANS方程进行数值计算,对M910旋转稳定弹丸在不同马赫数和转速条件下的气动参数和流场特性进行计算,计算结果表明:基于SST湍流模型的RANS方法,对亚音速和跨音速阶段的马格努斯力矩不能进行准确的预测。刘周等 [18] 研究发现对高速旋转的弹丸大攻角范围RANS方程的计算结果与试验数据存在一定的差异,采用延迟分离涡模拟(DDES)方法的计算结果有较为明显的改善刘周等 [18] 研究发现对高速旋转的弹丸大攻角范围RANS方程的计算结果与试验数据存在一定的差异,采用延迟分离涡模拟(DDES)方法的计算结果有较为明显的改善。显示出DDES方法具有更大的潜力,以提高旋转弹箭马格努斯效应的数值模拟精度。
工作主要是针对M910弹丸亚声速和跨声速Magnus力矩难以精确计算的问题,通过RANS-LES混合方法(DDES方法)和RANS方法的比较分析,确认两种方法在不同速度范围内的适用性。通过分析M910弹丸的尾迹流动,探讨了影响马格努斯力矩的背后流动机理。
旋转弹丸在飞行时会产生额外的侧向作用力–马格努斯力旋转弹丸飞行时会产生一个额外的侧向力——马格努斯力 [1] [2] 。马格努斯力引起的马格努斯力矩却可以影响弹丸的航向动稳定性,降低命中精度,因此,准确预测旋转气动特性成为弹箭研制的重要课题。然而由于复杂的气动干扰,比如低速尾迹流动与与强迫的旋转运动的耦合,使作用在弹箭上的气动力和气动力矩呈现较强的非线性非定常特性,为准确预测弹箭的气动特性提出了挑战。
20世纪80年代以来,国内外针对飞行器旋转空气动力效应开展了大量的研究工作。Vishal [3] 采用时间精确的雷诺平均Navier-Stokes方程(RANS)计算了Finner滚转阻尼和马哥努斯力矩,但轴向力与试验值 [4] 相比偏高。DeSpirio [5] 对M910旋转弹丸绕流场进行了数值模拟,结果显示在亚声速和跨声速来流下,采用RANS/LES混合的DES湍流模型计算马格努斯力矩与实验值符合更好。RANS/LES混合方法的基本思想是采用RANS高效可靠地模拟高频小尺度运动占主导地位的近壁区域,同时采用LES准确计算低频大尺度运动占优的非定常分离流动区域。RANS-LES混合方法是当前有限计算资源条件下处理高雷诺数大分离流动的合理选择,已经在多种流动类型的模拟中得到广泛的应用 [6] [7] [8] [9] 。
国内学者,主要采用工程方法或者求解RANS方法计算旋转弹丸的马格努斯力矩 [10] - [16] 。陈东阳等 [17] 选用剪切应力输运(shear stress transfer, SST)湍流模型,通过求解RANS方程,对M910旋转稳定弹丸不同马赫数、不同转速情况下的气动参数及流场特性进行数值计算,计算结果表明:基于SST湍流模型的RANS方法可以较好地计算阻力、法向力、俯仰力矩和压心系数,不能准确预测亚音速和跨音速阶段旋转马格努斯力矩。刘周等 [18] 研究发现对高速旋转的弹丸大攻角范围RANS方程的计算结果与试验数据存在一定的差异,采用延迟分离涡模拟(DDES)方法的计算结果有较为明显的改善,对比研究表明分离点位置对马格努斯效应有着显著影响。表明DDES方法对于提高旋转弹箭马格努斯效应的数值模拟精度有较大的潜力。
本文工作主要针对M910弹丸亚声速和跨声速马格努斯力矩难以准确计算问题,通过RANS-LES混合方法(DDES方法)和RANS方法的对比分析,确认两种方法在不同速度范围的适用性。通过分析M910弹丸的尾迹流动,对影响马格努斯力矩的背后流动机理进行探讨。
2. 数值方法
本文中采用非定常的数值模拟,非定常时间离散采用双时间步方法,物理时间层采用二阶向后差分,伪时间层采用LU-SGS隐式时间推进。计算采用格心格式的非结构有限体积法,Roe格式计算无粘通量。
对于非定常RANS方法,考虑了Spalart-Allmaras (SA)和Menter κ-ω SST两种湍流模型 [19] ,后文可见两种湍流模型的计算结果基本一致,因此只针对SA模型构造了相应的RANS-LES混合的DDES混合模型。DDES混合模型通过引入延迟函数
重新构造了长度尺度
[20] :
其中
为RANS湍流模型长度尺度,
为DES湍流模型长度尺度。当
趋于0时,采用RANS模型计算,当
趋于1时,采用DES模型计算。
3. 数值模拟结果和讨论
3.1. 模型、网格与计算状态
计算模型M910弹丸的几何尺寸如图1所示,由铝质鼻帽和钢质弹身构成,其中鼻尖直径为0.22 cm,鼻帽段锥体长度为4.12 cm;圆柱段直径1.62 cm,长度为3.27 cm;底部为一长度为0.2 cm的倒角构成。弹丸质心位于距鼻尖4.99 cm处,是后文中所有力矩的计算参考点。
计算状态如表1所示,来流马赫数横跨亚、跨、超声速三个速度范围,在不同的马赫数下有对应的绕x轴的旋转速度,来流的压力都为101,325 Pa,来流温度为288 K,计算攻角为3˚。
计算网格为六面体网格,弹体表面网格如图2所示,其中沿弹体流向布置135个点(其中锥体段70个网格点,圆柱段50个网格点,倒角段15个网格点)。为能适应亚声速计算,计算域的外边界距离弹体表面8倍弹体长度,整个计算域划分为两个外O-Block,其中在包围弹体的外O-Block如图3所示,边界层网格内法向布置50个点,第一层的网格厚度约为0.56 μm。随着来流速度的增大,边界层厚度不断减小,第一层的网格厚度也要求越来越小;图4为α = 6.34˚状态,y+沿弹体表面分布情况(在xy平面的截线),可见整个弹体表面都满足条件y+ ≤ 1。
3.2. 计算结果讨论
图5为阻力系数随马赫数的变化曲线,SA-DDES湍流模型的计算结果在整个马赫数范围都与实验数据吻合较好。其中PRDDAS软件为利用已有的实验数据而进行估算的半经验工程方法,在弹丸的早期设计中获得了广泛的应用在Ma < 2.5范围,SA湍流模型的计算结果与实验数据相比稍有偏大;而在Ma > 2.5范围与实验数据和DDES的计算结果都基本一致。表明亚声速和跨声速采用DDES方法可一定程度提高阻力的预测精度,而在超声速范围,采用RANS方法就可获得较为准确的阻力系数。
Figure 3. Schematic diagram of O-Block outside the model
图3. 模型外O-Block示意图
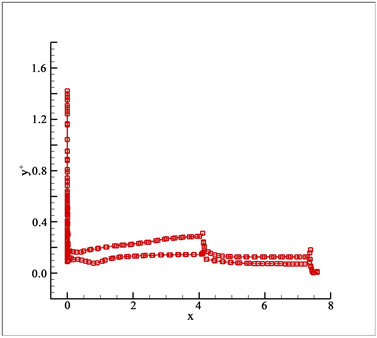
Figure 4. Distribution of y+ on the pitch plane along the axial direction
图4. 俯仰平面沿轴向y+分布
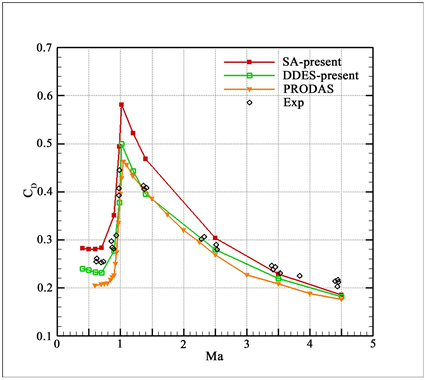
Figure 5. Variation curve of resistance coefficient with Mach number
图5. 阻力系数随马赫数的变化曲线
图6为法向力系数随马赫数的变化曲线,在整个马赫数范围SA湍流模型的计算结果都与DDES的计算结果吻合较好,尤其在超声速区域,两种方法的计算结果几乎完全吻合,且相比于PRODAS的估算结果更接近于实验数据的分布。且在跨声速区Ma = 1处,SA湍流模型与DDES的计算结果存在明显的峰值,这与实验观测到的Ma = 1处的升力峰值相一致,而PRODAS因缺乏激波预测模型,所以其结果未能反映该现象。
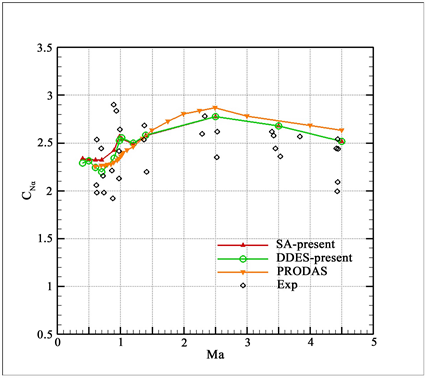
Figure 6. Variation curve of normal force coefficient with Mach number
图6. 法向力系数随马赫数的变化曲线
图7为俯仰力矩系数随马赫数的变化曲线,PRDDAS因缺乏激波预测模型,其预测结果在Ma > 2.5的范围偏高,而在跨声速范围内又偏低;而SA湍流模型的计算结果在整个马赫数范围都与DDES的计算结果及实验数据吻合较好。
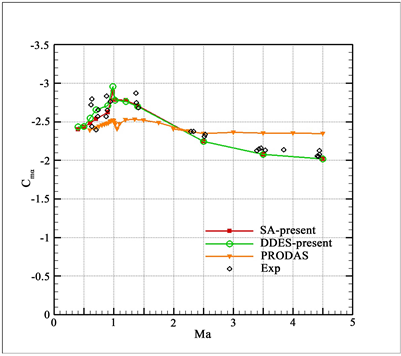
Figure 7. Variation curve of pitch moment coefficient with Mach number
图7. 俯仰力矩系数随马赫数的变化曲线
图8法向力压心随马赫数的变化曲线。整个马赫数范围都CFD计算结果都与实验数据吻合较好;法向力压心的变化趋势与法向力系数和俯仰力矩系数的变化规律相一致,根据定义法向力压心由这两个系数计算等到。
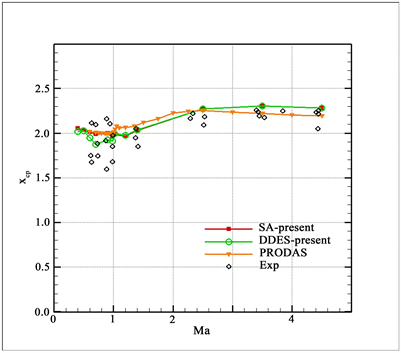
Figure 8. Variation curve of normal force pressure center with Mach number
图8. 法向力压心随马赫数的变化曲线
滚转阻尼与马格努斯力矩系数是研究旋转弹丸最重要的两个参数,图9滚转阻尼系数随马赫数的变化曲线。在整个马赫数范围SA湍流模型的计算的滚转阻尼系数都与DDES的计算结果几乎完全重合,在Ma < 1.8的范围也与PRODAS的预测的结果基本一致。CFD的计算结果与实验数据的分布比较整体偏高,但随马赫数的变化趋势基本相同。
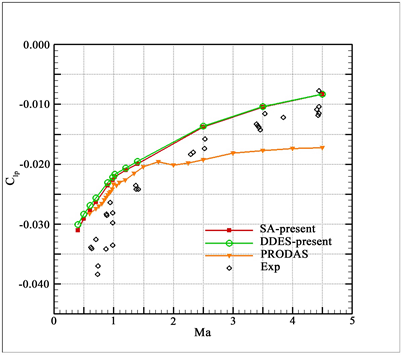
Figure 9. Curve of rolling damping coefficient changing with Mach number
图9. 滚转阻尼系数随马赫数的变化曲线
图10马哥努斯力矩系数随马赫数的变化曲线。在Ma < 1.4范围,SA湍流模型、Despirito的定常RANS方法和PRDDAS工程方法都不能预测马格努斯力矩系数的急剧下降趋势。而SA-DDES湍流模型因加入了延迟分离涡模型,其计算结果能与实验数据吻合较好,且延迟分离涡模型比原来的分离涡模型稳定性更好,所以比Despirito的DES计算结果规律性更好;在Ma > 2.5范围,实验测量及CFD计算的
都接近于0,表明马格努斯力压心与重心的位置非常接近,使得在弹道范围测量马格努斯力矩较为困难,增大了实验的不确定度。
图11为来流Ma = 0.6时RANS湍流模型和DDES湍流模型计算的等Ma数云图。可见RANS方法和DDES混合方法的主要差异在于尾迹流动。DDES湍流模型得到的非定常的尾迹流动,而RANS湍流模型得到的是定常的尾迹。
4. 结论
本文针对M910弹丸,从亚声速到超声速通过与试验结果的比对,对比研究了RANS-LES混合方法(DDES方法)和RANS方法的适用性,得到了如下结论:
1) 从亚声速到超声速,对于法向力,俯仰力矩、法向力压心和滚转阻尼,采用RANS方法计算的结果就与实验数据吻合较好,偏差在10%之内。
2) 对于阻力系数,RANS方法预测的阻力系数与试验值相比偏高,随着Ma的增大两者的差异逐渐减小。而DDES混合方法的计算结果在整个马赫数范围都与实验数据吻合较好。
3) 对于马格努斯力矩,在亚声速和跨声速范围,RANS方法计算的结果与试验差异较大,而DDES混合方法与试验吻合较好,且与DES方法相比规律性更好。

Figure 10. Variation curve of magnus moment coefficient with Mach number
图10. 马哥努斯力矩系数随马赫数的变化曲线
亚声速和跨声速范围,RANS方法和DDES混合方法的主要差异在于尾迹流动,RANS方法得到的是定常尾迹,而DDES混合方法得到是非定常尾迹。