焦炭在空气中的燃烧动力学研究

The Coke Burning in the Air Dynamics Research

摘要: 焦炭燃烧的研究是重中之重，对于优化焦炭的燃烧性能，提高能源利用率具有重要意义。目前焦炭燃烧动力学面临的挑战之一是建立准确的反应机理模型，而且如今关于燃烧动力学的低温度区域的模型建立的研究较少，所以本实验以加入600℃燃烧反应数据作为前提下，利用高温立式管式炉对焦炭进行燃烧动力学反应特性测试。本实验采用均相模型、未反应收缩核模型对焦炭的燃烧动力学数据进行计算，经过等转化率法计算得到的燃烧反应活化能对其进行判定。实验所得结果，均相模型计算的活化能处在低转化率的活化能范围内，未反应收缩核模型计算的活化能处在高转化率的活化能范围内。经结果发现，600℃焦炭燃烧符合建立的模型，并且一种模型不能概括整个焦炭燃烧过程。

Abstract: The study of coke combustion is of utmost importance, and it is of great significance for optimizing the combustion performance of coke and improving energy utilization efficiency. One of the challenges facing coke combustion kinetics currently is to establish an accurate reaction mechanism model, and there is currently limited research on the establishment of models for the low temperature region of combustion kinetics. Therefore, in this experiment, the combus-tion kinetics reaction characteristics of coke were tested using a high-temperature vertical tube furnace with the addition of 600 ˚C combustion reaction data as the premise. This experiment uses a homogeneous model and an unreacted shrinkage core model to calculate the combustion kinetics data of coke, and the activation energy of the combustion reaction calculated by the equal conversion method is used to determine it. The experimental results show that the activation energy calculated by the homogeneous model is within the range of low conversion rates, while the activation energy calculated by the unreacted shrinkage core model is within the range of high conversion rates. Through the results, it was found that the combustion of 600 ˚C coke conforms to the established model, and one model cannot summarize the entire coke combustion process.

1. 引言

作为化学燃料之一的焦炭是高炉炼铁生产中不可缺少的原料，焦炭在高炉炼铁过程中主要起到四个作用 [1] [2] [3] ，分别是发热剂、还原剂、渗碳剂和料柱骨架作用。随着钢铁工业的快速发展，焦炭的大量燃烧导致全球变暖愈加严重 [4] ，焦煤资源越来越匮乏，炼铁成本越来越高 [5] 。通过高炉风口喷吹煤粉替代焦炭在高炉内的部分作用，在一定程度上降低焦比和冶炼成本 [6] ，但是随着喷煤量的增加，入炉焦炭减少，料柱透气性变差 [7] ，因此，如何减少焦炭的消耗，维持其在高炉内的强度，对高炉的生产就显得极为重要。焦炭在风口区燃烧是其在高炉内的主要消耗，研究焦炭在空气中的燃烧反应动力 [8] [9] 学具有实际价值。

王珊 [10] 等人通过采用Coast-Redferm法对3种生物质焦(玉米秸秆、小麦秸秆和松木屑)计算平均活化能，分别为8.976，9.11和15.081 kJ/mol，根据DAEM模型求得分布活化能为45.34~57.31 kJ/mol，54.22~65.34 kJ/mol，68.67~76.24 kJ/mol，而在参混5%的无烟煤焦后，玉米秸秆和小麦秸秆焦反应活化能均增大，反应后期下降趋势显著；王淦 [11] 等在焦炭燃烧颗粒燃烧数值模拟实验中发现焦炭粒度对燃烧性能的影响大于氧体积的影响，并且焦炭单颗粒的减小会导致燃烧速率降低和燃尽时间降低，等重量焦炭燃烧时，小颗粒焦炭燃烧速率远大于大颗粒焦炭；刘浪 [12] 等人通过烟煤添加生物质混燃实验探究生物质对燃烧特性的影响，生物质的添加降低了着火温度，并且发现添加生物质的样品燃烧反应性能有所增加，随着生物质比例增加，燃烧性能提升逐渐明显。

2. 实验部分

2.1. 实验原料

本实验所用焦炭来源于唐钢美景煤化工有限公司，其工业分析如表1所示。

Table 1. Industrial analysis parameters of coke

表1. 焦炭工业分析参数

注：*Mad：空气干燥基水分，Ad：干燥基灰分，Vdaf：干燥无灰基挥发分，St：全硫，G：粘结指数，X：胶块最终缩度，Y：胶质层最大厚度胶质层最大厚度。

图1为焦炭的为X射线衍射图，1峰为碳峰，由C微晶组成，表示C微晶的定向程度，2峰为的微晶成分为Al₂(Al_2.8Si_1.2)O_9.6，属于莫来石的一种，具有良好的耐火性和高温稳定性，3峰为SiO₂，为焦炭中主要的灰分物质。

Figure 1. Coke XRD

图1. 焦炭XRD

2.2. 实验设备及流程

焦炭空气燃烧动力学实验装置为高温立式管式炉，设备是由以硅钼棒为发热体的高温节能管式炉、精度为0.0001 g的电子天平和计算机三部分构成。实验时将用自制坩埚放到炉管恒温区，坩埚的另一端同电子天平的底部相连，目的是测得坩埚的重量。电子天平和计算机通过电子传感器相连，可将坩埚的实时重量传送至计算机，计算机每隔5 s采集一次数据，通过计算机检测炉内坩埚实时重量变化。

实验首先将高温立式管式炉分别升温至600℃、800℃、850℃、900℃、950℃、1000℃、1050℃，并保持恒温。实验所用焦炭粒度为1~3 mm，并将焦炭均匀的平铺到坩埚中，称重记录，打开炉体上下两部分气阀，使空气可以在炉体中流通，将坩埚放入高温立式管式炉，对坩埚重量进行实时监控，待重量趋于稳定，将坩埚取出，冷却到室温并称重记录。焦炭燃烧转化率表达式见公式(1)：

$x=\frac{m-m_t}{m-m_1}$ (1)

式中，x——焦炭燃烧转化率；

M——焦炭初始重量；

m_t——t时刻焦炭重量；

m₁——燃烧后剩余焦炭重量。

反应速率能够表征焦炭的燃烧的反应活性，表示为：

$R=\frac{\text{d}x}{\text{d}y}=kf\left(x\right)$ (2)

式中：f(x)——焦炭燃烧反应机理函数；

K——燃烧反应本征反应速率常数：

$k=k_0\exp \left(-\frac{E}{RT}\right)$ (3)

3. 实验结果和分析

图2(a)为800~1050℃的焦炭燃烧失重曲线；图2(b)为600℃焦炭燃烧失重曲线以及燃烧反应速率，与图2(a)中的失重曲线有明显差别，焦炭燃烧开始大量失重的时间370 min；图2(c)为800~1050℃的焦炭燃烧反应速率，随着燃烧温度的上升失重速率越高，完全燃烧所需时间越短，与潘宗林 [13] 的淮南煤焦动力学研究规律一致。焦炭燃烧分为3个阶段，第1阶段焦样表面快速升温，极短时间内上升到炉温度；第2阶段中的水分受热挥发和挥发分的析出，因为在坩埚放入高温立式管式炉中时，焦炭温度迅速升高，在极短的时间内焦炭中的水分和挥发分会快速析出并释放热量，加快焦炭表面温度的提升，第3阶段，为燃尽阶段，主要将剩余的未完全燃烧的焦炭烧完，此阶段的焦样中大部分固定碳已经反应完毕，但是随着坩埚边缘的焦炭燃烧所产生的部分灰分还会覆盖到剩余未反应的焦炭表面，导致焦炭反应的过程减缓，燃烧速度较为缓慢。对比图2(a)~(c)，600℃与800~1050℃的失重曲线和反应速率整体趋势明显不同，600℃焦炭开始大量失重后的曲线向后推移，因为在较低温度下，燃烧初始热量积累较为缓慢，焦炭自身温度上升趋势不明显，但燃烧后曲线趋势与800~1050℃的曲线趋势基本一致，猜想较低温度区曲线是否符合模型，所以加入600℃的曲线进行求证。

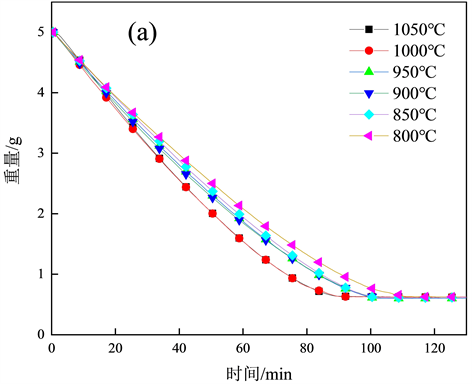
(a) 800~1050℃时间–重量关系；

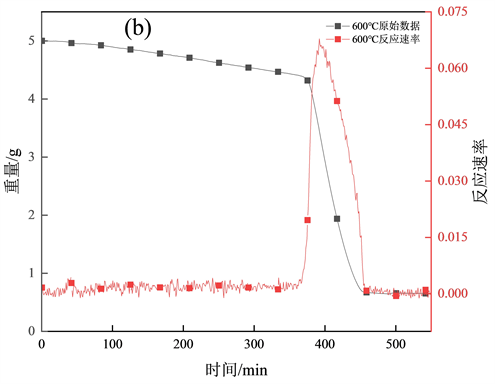(b) 600℃时间–重量–反应速率关系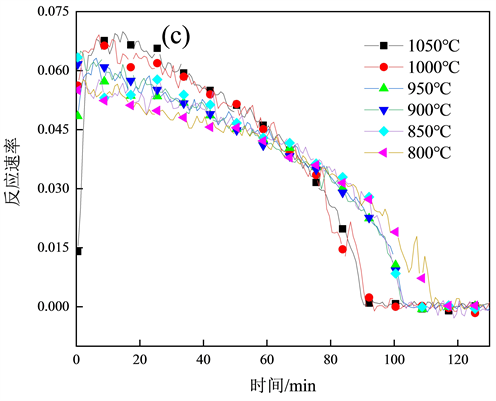；(c) 800~1050℃时间–反应速率关系。

Figure 2. Weightlessness curve under different temperatur

图2. 不同温度下的失重曲线

3.1. 燃烧温度影响消除

实验以5 ± 0.0005 g作为实验初始焦炭重量，恒温温度为600℃、800℃、850℃、900℃、950℃、1000℃、1050℃，粒度为1~3 mm，以此为燃烧反应实验环境，如图3所示，1050℃和1000℃，950℃和900℃，850℃和800℃的曲线十分接近，表明焦炭在空气气氛下条件下燃烧，50℃的温度涨幅对于焦炭燃烧影响较小，为排除燃烧温度影响，在1050℃和1000℃，950℃和900℃，850℃和800℃之间各取一个温度作为研究对象进行动力学分析。实验选取1000℃、900℃、800℃、600℃作为实验研究对象。

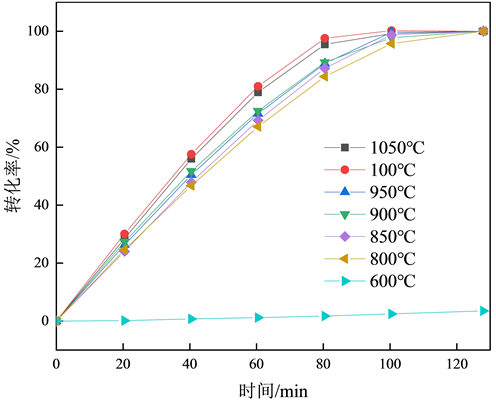
Figure 3. Relationship between combustion temperature and conversion rate

图3. 燃烧温度与转化率关系

3.2. 焦炭燃烧过程分析

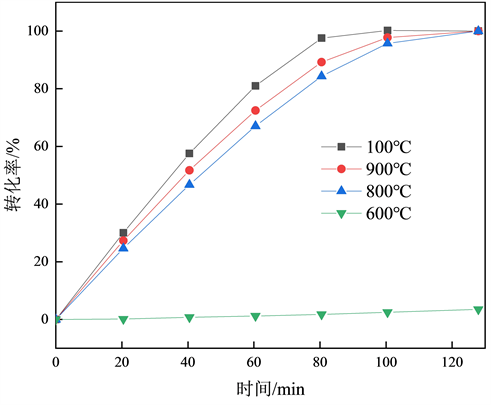
Figure 4. The relationship between conversion rate and time

图4. 转化率与时间的关系

转化率与时间的关系如图4，800~1000℃的曲线转化率达到100%的时间在120 min以内，600℃转化率达到100%的时间为470 min，相同时间内1000℃转化率最高，600℃转化率最低，说明随着燃烧温度的升高，焦炭中的C元素与空气中O₂反应更加剧烈。

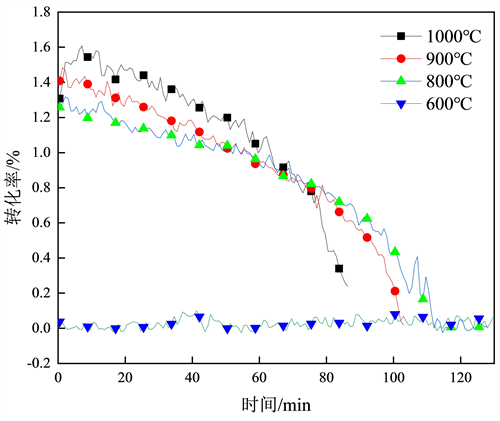
Figure 5. The relationship between reaction rate and time

图5. 反应速率和时间关系

图5为图4曲线微分所得，图中1000~800℃燃烧反应速率随着时间的增加而逐渐减少，并且3条曲线存在一个共同交点，其相交的时间区域在60~80 min之间，在交点之前其反应速率1000℃最高，800℃最低，而交点后燃烧反应速率相反，说明在60~80 min的时间区域焦炭中的C元素基本反应完毕，只有少量的C未反应，在60~70 min之前为焦炭中C大量转化的时间区域。

4. 焦炭燃烧反应动力学模型

焦炭燃烧反应模型选择有很多种，包括均相模型、未反应收缩核模型、混合反应模型、分布活化能模型和随机孔模型等，本实验所采用的模型为均相模型和未反应收缩核模型。

4.1. 均相反应模型

均相反应模型是气固反应中最简单的模型。模型通过假设气体与煤焦在颗粒内部和外表面同时发生反应，把煤焦燃烧非均相反应简化为均相反应 [14] 。当燃烧反应为一级反应时，燃烧机理函数 $f\left(x\right)=1-x$ ，燃烧反应速率可以表示为：

$\frac{\text{d}x}{\text{d}y}=k\left(1-x\right)$ (4)

对式(4)积分得到：

$-\ln \left(1-x\right)=kt$ (5)

由实验数据回归 $-\ln \left(1-x\right)$ 与t关系见图6。

Figure 6. Homogeneous model

图6. 均相模型

4.2. 未反应收缩核模型

未反应收缩核模型 [15] 建立的基础是气体与固体的反应只发生在固体表面，反应过程中，气体会逐步渗入固体之中，待到反应完成，形成一个未反应核心，反应速率与未反应核外表面积成正比，经过推导得到反应速率微分方程：

$\frac{\text{d}x}{\text{d}y}=k{\left(1-x\right)}^{2/3}$ (6)

对式(6)积分得到转化率x与时间t关系：

$3\left[1-{\left(1-x\right)}^{1/3}\right]=kt$ (7)

根据式(7)对实验数据线性回归得到实验值和模型计算值如图7所示：

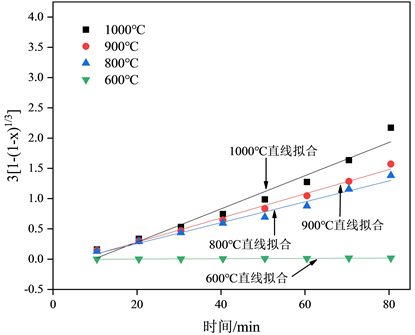
Figure 7. Unreacted shrinking core model

图7. 未反应收缩核模型

4.3. 动力学参数求取

均相反应模型和未反应收缩核模型，分别根据图6和图7中回归直线的斜率计算得到不同温度下煤焦燃烧反应速率常数。

对式(3)等号两边取自然对数得到：

$\ln k=\ln k_0-\frac{E}{RT}$ (8)

根据不同温度下计算得到的k值，由式(8)回归计算活化能E (斜率)和指前因子k₀ (截距)，不同模型回归直线如图8所示。

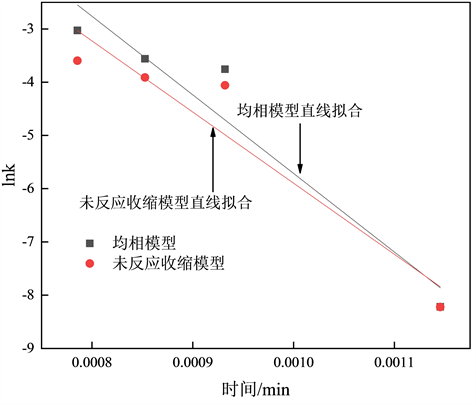
Figure 8. Homogeneous model and unreacted shrinking core model t-lnk figure

图8. 均相模型和未反应收缩核模型t-lnk图

采用不同模型计算得到的反应速率常数k、活化能E和指前因子lnk₀如表2所示：

Table 2. The calculation results of the homogeneous model and the unreacted shrinking kernel model

表2. 均相模型和未反应收缩核模型的计算结果

4.4. 动力学模型比较

不同反应模型因为选取的机理函数不同得到的动力学参数也有所差别。为了避开反应机理函数的选择，采用等转化率法 [16] [17] 计算动力学参数来确定反应最佳模型。计算过程如下：

把式(1)代入式(2)得到：

$\frac{\text{d}x}{\text{d}y}=f\left(x\right)k_0\exp \left(-\frac{E}{RT}\right)$ (9)

对机理函数f(x)积分：

$G\left(x\right)=k_0\exp \left(-\frac{E}{RT}\right)t$ (10)

等号两边取自然对数并变形：

$\ln t=\ln \frac{G\left(x\right)}{k_0}+\frac{E}{RT}$ (11)

在相同的实验条件下，当转化率固定时，等号右边第一项为常数，因此等号两边lnt和1/T为线性关系，由斜率E/R可计算得到活化能E。分别选择转化率x为10%、20%和30%和x为40%、50%和90%时得到lnt和1/T关系如图9和图10所示：

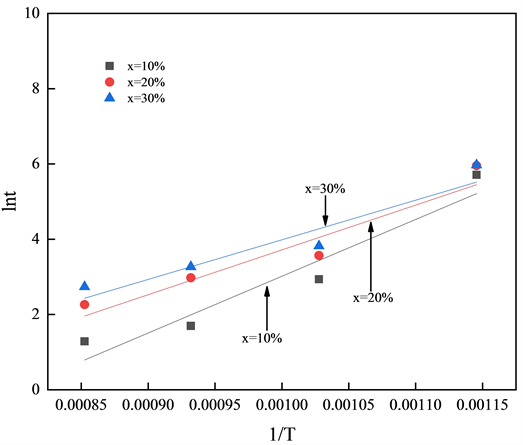
Figure 9. Equal conversion method with low conversion rate

图9. 低转化率的等转化率法

由斜率计算得到不同转化率下燃烧反应活化能，低转化率下活化能处于124.011~150.107 kJ/mol之间，高转化率下活化能处于124.011~65.528 kJ/mol之间，均相模型所得活化能在低转化率(转化率为0~30%)条件下更合适，而未反应收缩核模型所得活化能在低转化率(转化率为30~90%)条件下更合适。

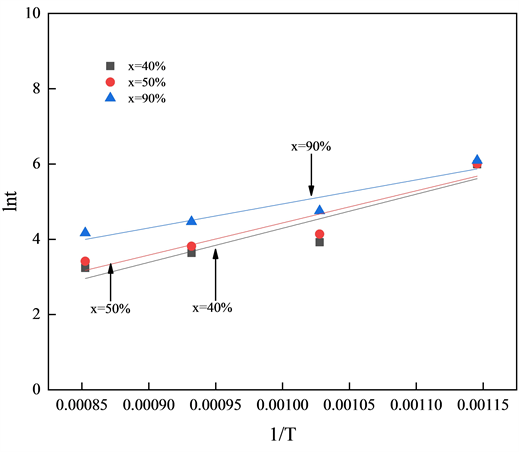
Figure 10. Equal conversion method with high conversion rate

图10. 高转化率的等转化率法

5. 结语

1) 在加入600℃焦炭燃烧失重曲线前提下，两种模型计算的燃烧反应的活化能分别为146.254 kJ/mol和111.058 kJ/mol，lnk₀分别为9.04498和7.4618。

2) 为避开反应机理函数的选择，采用等转化率法计算得到燃烧反应活化能，低转化率下活化能处于124.011~150.107 kJ/mol之间，高转化率下活化能处于96.405~65.528 kJ/mol之间，经过对比，均相模型计算结果与低转化率的计算结果相近，未反应收缩核模型计算结果更加接近高转化率的计算结果。

基金项目

河北省自然科学基金(E2018209323、E2022209125)。

NOTES

^*第一作者。

^#通讯作者。