1. 引言
国际社会普遍认为,二氧化碳过度排放是引起气候变化的主要因素。人类活动排放的二氧化碳等温室气体导致全球变暖,加剧气候系统的不稳定性,导致一些地区干旱、台风、高温热浪、寒潮、沙尘暴等极端天气频繁发生,强度增大,极端天气为我们的日常生产生活带来了诸多不便,全球生态平衡时刻遭到破坏。目前,全球范围内能源及产业发展低碳化的大趋势已经形成。我国近年来减排成效显著,2019年碳排放强度比2005年下降48.4%。2020年9月22日,习近平主席在第七十五届联合国大会一般性辩论上提出中国将提高国家自主贡献力度,采取更加有力的政策和措施,二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和 [1] 。“双碳”目标是着力解决资源环境约束突出问题、实现中华民族永续发展的必然选择,是构建人类命运共同体的庄严承诺。通俗来讲,碳达峰 [2] 指二氧化碳排放量在某一年达到了最大值,之后进入下降阶段;所谓的“碳中和” [3] ,就是在一定时期内,由某一组织或某一群体所产生的二氧化碳,可以被自然或人为的手段所吸收或抵消,从而达到“零排放”的目的。
于中国而言,作为全球第二大经济体和最大的发展中国家,中国经济和社会各行各业正呈现蒸蒸日上的发展态势,而这背后需要庞大的资源和能源支撑,大量资源和能源消耗的同时也会带来二氧化碳排放的进一步增加 [4] ,在2020年,全球能源碳排放340亿吨,中国碳排放99亿吨,占全球碳排放的29% (如图1所示),但是随着中国社会主义现代化建设的逐步完善,以及绿色低碳等创新技术的广泛应用,二氧化碳排放总量终将迎来下降的拐点,即“碳达峰”目标,因此,实施“双碳”目标刻不容缓。要想在2060年实现“零排放”,就需要解决“发展”与“减排”的矛盾。在这些问题中,最突出的问题是如何促进经济和社会的高质量发展。经济增长、碳排放量与能源消费量之间必然存在着关联关系 [5] ,要想做到节能减排,必须从提高能源使用效率、增加非化石能源消费比例着手,才能实现经济增长与碳排放的逆向转化。
本文根据“华为杯”第二十届中国研究生数学建模竞赛D题提供的数据,该数据假定位于中国东南沿海,地势平坦,水陆交通便利,人口密集,经济发达,科教资源丰富,但能源及生态碳汇资源相对匮乏,因此此数据能更准确的预测区域的碳排放量与各个指标之间的关系。该数据以Excel格式给出,时间范围从2010年至2020年,历史数据的基期是2010年,十二五时期为2011~2015年;十三五时期为2016~2020年。数据内容包括:人口、总产值(GDP)及三次产业与部门的产值分布、总能耗及三次产业与部门的能耗分布、总能耗及化石能源与非化石能源品种分布、能源消费的三次产业与部门的品种结构、碳排放量总量及产业与部门的分布、碳排放量的三次产业与部门的能源品种结构以及碳排放量相关各类能源的碳排放因子。首先对数据进行预处理操作,包括降维、异常值、缺失值检测等;利用Python寻找缺失值,对于存在异常的缺失值使用KNN算法进行填充处理。通过选定指标及构建体系,对碳排放以及人口、经济、能源消费量的现状进行分析,并建立关联关系模型,深入研究这些因素之间的相互关系。利用处理之后的数据进行进一步处理,建立回归预测模型。使用不同的预测模型(线性回归 [6] 、Xgboost [7] 、LSTM [8] 、灰色预测 [9] 、随机森林 [10] 等)对进行人口和GDP的预测,建立基于人口和经济变化的能源消费量预测模型。然后使用多元线性回归模型描述碳排放量与人口、GDP和能源消费量之间的关系,以及碳排放量与各能源消费量部门和能源品种的关系。根据预测结果,可以确定最合适的路径和措施,以实现双碳目标,同时考虑全球碳排放趋势、新能源技术和新能源消费模式等因素,为制定更全面和可行的碳达峰和碳中和战略提供更多参考。
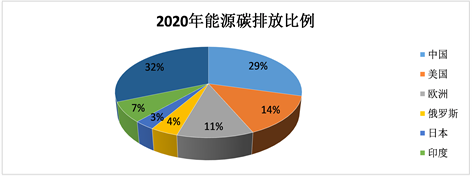
Figure 1. China’s carbon emissions from energy in 2020
图1. 2020年中国能源碳排放量比例
2. 建立线性关系
2.1. 数据预处理
首先利用Python对给出的数据进行异常缺失值的查找,经过查找得到数据中的异常值在表格中表示为“-”。以能源消费部门碳排放因子数据表格为例,数值栏中“-”表示该年该项能源未使用,无法计算实际的碳排放因子。在第三产业的建筑消费部门中煤炭的碳排放因子数据中存在数据缺失的情况,如表1所示,2012年的数据被认定为异常缺失值。
为了保证结果的准确性,不能直接忽略该种缺失值。根据具体情况和需求,在本文的研究中,采用了插值填充方法。在插值填充方法中,基于KNN算法 [11] 的数值插补方法是一种有效的异常缺失值处理方法。这种方法可以利用已有数据的特征和相似性,通过寻找最近邻样本来预测并填补缺失值。相比于其他插值填充方法,基于KNN算法的数值插补方法更能保持数据的完整性,并有效降低数据分析和建模过程中的偏差。
调用sklearn库的impute模块中的KNNImputer函数可以实现该算法,将数据导入进行计算,得到部分结果如表2所示。

Table 2. The result of the processing
表2. 处理后的结果
2.2. 构建指标评价体系
为了更加全面和准确地构建指标评价体系 [12] ,首先需要根据提供的数据和需要解决的问题,选择主要指标,即一级评价指标。这些一级评价指标包括区域经济、人口、能源消费量以及碳排放量。
根据给出的数据文件,对于人口指标,将常驻人口总量作为其二级指标;对于经济指标,选择GDP总量、第一产业(农林消费部门)、第二产业(总量、能源供应部门以及工业消费部门)、第三产业(总量、交通消费部门以及建筑消费部门)作为其二级指标;对于能源消费量,选择总量、化石能源消费和非化石能源消费作为二级指标;对于碳排放量,选择排放总量、与各部分碳排(农林消费部门、工业消费部门、第三产业总量、第三产业交通消费部门、第三产业建筑消费部门、居民生活消费)作为二级指标。
2.3. 现状分析
为了更加直观的观察分析某区域十二五(2011~2015年)和十三五(2016~2020年)期间的碳排放量状况,将给出的数据集进行拆分,利用Excel绘制十二五、十三五时间下变化趋势,如图2所示。
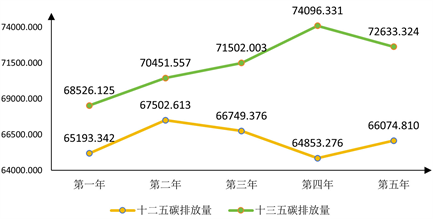
Figure 2. Trends in carbon emissions during the 12th and 13th five-year plans
图2. 十二五、十三五期间碳排放量变化趋势
通过折线图,可以较为清晰的看出,十三五期间的碳排放量明显高于十二五期间。对于十二五期间而言,中间三年的碳排放量有明显下降趋势;十三五期间前面四年的碳排放量一直保持上升的趋势。为了能直观的看出不同时期的增长率,本文计算了十二五、十三五期间碳排放量的增长率,绘制为柱状图如图3所示。

Figure 3. The growth rate during the twelfth and thirteenth five-year plans
图3. 十二五、十三五期间增长率
通过柱状图,可以清晰的观察到,在十三五计划末期碳排放增长率已经开始降低,而十二五末期碳排放增长率开始上升。
为了更加直观的看各个指标之间的关系,绘制指标之间的散点图观察变化趋势。如图4、图5所示。
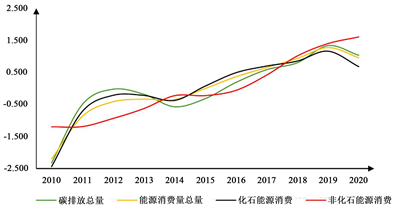
Figure 5. Carbon emissions and energy consumption
图5. 碳排放量与能源消费相关图
通过散点图,可以看出大部分指标都与碳排放量呈现一定的正相关。为了更加客观地判定结果,这里可以建立相关性分析模型,引入person相关性,判断指标之间的关系。其中样本协方差、样本标准差和样本皮尔逊相关系数的公式分别如(1)、(2)、(3)、(4)所示。
(1)
(2)
(3)
(4)
利用相关系数研究大部分指标都与碳排放量的相关关系,得到相关性分析结果如表3所示,这里首先展示二级指标之间的相关性。

Table 3. Correlation of secondary indicators
表3. 二级指标相关性
为了更加直观的看出指标间的相关性,这里利用origin绘制了矩阵热力图,如图6所示。
通过相关性分析图表的可视化结果,本文可以看出经济指标与能源消费量之间具有较好的相关性。同时对几个多维一级指标进行降维处理,将结果导入关联分析模型,得到下面的结果,如表4所示。

Table 4. Results of correlation analysis
表4. 相关性分析结果
注:***、**、*分别代表1%、5%、10%的显著性水平。
通过上述分析,本文可以得出以下结论:
1) 对于这四项一级指标大部分都具有较好的相关性;
2) 除了能源消费量与其他三个指标的相关性不太明显。
3. 建立预测模型
通过对数据集的分析,常驻人口总量与年份之间有着一定的线性关系,所以选择线性回归模型进行预测,而常驻人口的变化量通常还与经济,能源消费量有关,因此为了得到更好的预测结果,可以将经济变化指标相关因素,能源消费量作为常驻人口预测的特征。能源消费指标可以考虑煤炭消费量、油品消费量等,这些特征呈非线性关系。由于线性回归模型无法捕捉到序列中的非线性因素,而神经网络算法在处理非线性问题具有独特的优势,因此本文准备用另外两个机器学习模型(LSTM, XGboost)分别进行预测。LSTM时间序列 [13] 数据通常具有长期依赖性,意味着当前时间步的值受到之前时间步的值的影响,选择了多个特征进行模型预测。XGBoost模型 [14] 可以通过评估特征在决策树中的分裂贡献度或特征覆盖度来度量特征的重要性,再将各预测模型通过加权方法,得到最终的预测结果。
3.1. 线性回归预测
线性回归(Linear Regression)是确定两种或两种以上变量之间所存在的定量关系的一种统计方法,线性回归的数据集的形式为多个属性X与一个对应的Y,目的是求解X与Y之间的线性映射关系,优化求解参数的目标是降低预测值与Y之间的差别。它可以通过数据学习得到一个通过自变量的线性组合来进行预测因变量的函数,形式如下式所示:
(5)
大多数所见到的均为向量形式,如下:
(6)
其损失函数是单个样例的误差,具体形式为:
(7)
代价函数是对数据集整体的误差描述,也就是损失函数的总和的平均,具体形式为:
(8)
目标函数为了避免过拟合或者进行一些特殊目的的约束,一般在代价函数的后面加入正则化项:
正则化项
正则化项 (9)
为了对常驻人口进行预测,建立线性回归模型。建立线性回归模型,进行相关分析,如公式(10)所示:
(10)
其中,
服从正态分布,
为自变量系数,
为常数项系数。
表示第i年该地的常驻人口数量,
表示第i年。最终得到表5中的结果,如下所示。
注:***、**、*分别代表1%、5%、10%的显著性水平。
因此,得到的结果为公式(11)所示。
(11)
为了更加直观的观察二者的关系式,绘制了拟合示意如图7所示。
3.2. XGBoost模型预测
XGBoost是Extreme Gradient Boosting的缩写,称为随机梯度提升算法,是决策树算法的集合。XGBoost算法的思想是将许多弱分类器集成在一起,形成一个强分类器(个体学习器间存在强依赖关系,必须串行生成的序列化方法)。XGBoost的基本组成元素是决策树,这些组成XGBoost的决策树之间是有先后顺序的:后一棵决策树的生成会考虑前一棵决策树的预测结果,即将前一棵决策树的偏差考虑在内,使得先前决策树做错的训练样本在后续受到更多的关注,然后基于调整后的样本分布来训练下一棵决策树。优点如下:1) 精度高。XGBoost对损失函数进行了二阶泰勒展开,一方面为了增加精度,另一方面也为了能够自定义损失函数,二阶泰勒展开可以近似许多损失函数。2) 灵活性强。XGBoost不仅支持CART,还支持线性分类器;XGBoost还支持自定义损失函数,只要损失函数有一二阶导数。3) 防止过拟合。XGBoost在目标函数中加入了正则项,用于惩罚过大的模型复杂度,有助于降低模型方差,防止过拟合。
本文将建立XGboost模型,对常驻人口的数据进行预测。XGboost是由多个个基础模型组成的一个加法模型,在训练出一颗树的基础上再训练下一颗树,预测它与真实分布之间的差距,通过不断训练用来弥补差距的树,最终用树的组合实现对真实分布的模拟。
假设本文第t次迭代要训练的树模型是
,则有:
(12)
其中
是第t次迭代后样本的预测结果,
是前
的预测结果,
是第t棵树的模型。训练该模型通常是定义一个目标函数去优化它,而XGboost的目标函数包含损失函数和正则项两部分,损失函数代表模型拟合的程度,正则项被用来控制模型的复杂程度。其目标函数为如公式(13)所示:
(13)
XGboost的正则项是一个惩罚机制,叶子节点的数量越多,惩罚力度越大,从而限制他们的数量。惩罚项如公式(14)所示:
(14)
其中,
为惩罚力度,
为惩罚项,
为叶子节点T的系数。
3.3. LSTM模型预测
LSTM,长短时记忆网络(Long Short Term Memory Network, LSTM),是一种改进之后的循环神经网络,可以解决RNN无法处理长距离的依赖的问题,目前比较流行。LSTM (Long Short-Term Memory)通过门控机制和细胞状态的记忆能力,能够有效地捕捉和利用序列中的长期依赖关系(LSTM对时间序列的预测其结构如图8所示),在t时刻,LSTM的输入有三个:当前时刻网络的输入值
、上一时刻LSTM的输出值
、以及上一时刻的单元状态
;门的输出是0到1之间的实数向量,当门输出为0时,任何向量与之相乘都会得到0向量,这就相当于什么都不能通过;输出为1时,任何向量与之相乘都不会有任何改变,这就相当于什么都可以通过。
通过对数据集的分析,人口常驻总量随年份变化形成时间序列。时间序列数据通常表现出长期依赖性,即当前时间步的值受之前时间步的值的影响。传统的机器学习方法(如线性模型)难以捕捉这种长期依赖关系。因此,本文使用LSTM来捕捉这些非线性关系,同时选择使用多特征进行预测,从而提高预测的准确性。
为了消除不同场景由于不同因素造成的影响,采用最大/最小归一化方法对样本数据进行归一化处理,公式如下:
(15)
式中:X为原始样本数据;
为原始样本数据的最小值;
样本数据的最大值;x为归一化处理后的样本数据。
然后,本文需要选择网络输入与输出变量。具体地,选用三个核心指标的数据作为样本数据,确定网络输入变量的个数。
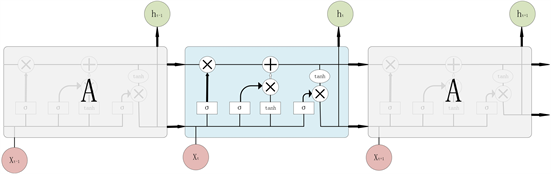
Figure 8. A schematic of the LSTM model
图8. LSTM模型示意图
其中,输入门,它决定了当前时刻网络的输入
有多少保存到单元状态
:
(16)
遗忘门,它决定了上一时刻的单元状态
有多少保留到当前时刻
:
(17)
输出门,控制单元状态
有多少输出到LSTM的当前输出值
:
(18)
候选记忆细胞计算:
(19)
将数据导入Matlab,利用编写的程序进行预测。其训练进度如图9所示:
4. 建立区域碳排放量预测模型
4.1. 加权预测模型
对于基于人口的能源消费量预测模型,需要考虑如何减小预测值与真实值的差距,提高该模型的预测精度,因此选择建立一个加权预测模型。该加权模型选择线性回归模型、XGboost预测模型和LSTM神经网络分别建立不同的子模型,然后对预测结果构建加权优化模型,以提高模型精度。
设
是同一个问题通过m种预测方法(每种方法都通过各自的检验)所得到的预测结果,
是第
种预测方法对原始数据
的模拟值。则这m种方法的加权预测值为:
(20)
其中,
表示第i种预测方法与第j个历史数据的模拟值之间的误差,记:
(21)
(22)
因此,本文将建立一个优化模型,将误差最小化作为目标函数,并且加上权重和为1的约束条件。然后,本文可以使用多目标粒子群优化算法 [15] 来求解该规划模型,相比直接使用lingo或matlab进行求解,这种方法可以减少计算量。
通过本文的规划模型,每个粒子确定每个粒子个体的最优解并从这些个体最优解找到一个全局最优值,这里涉及到了本文粒子的位置和距离公式,公式如下所示:
(23)
(24)
(25)
其中,
为0到1之间的随机数。
为惯性权重因子,其值非负。当
的数值较大时,该算法全局寻优能力强,局部寻优能力弱;当
的数值较小时,该算法全局寻优能力弱,局部寻优能力强。
的引入,可以极大地提升了粒子群优化算法的性能,使其能够根据不同的搜索问题调整全局和局部搜索的能力。同时在粒子群优化搜索的过程中对
进行动态化处理,这样可以获得更好的寻优结果,因此本文采用线性递减权值策略 [16] ,如公式(26)所示:
(26)
其中,
为最大迭代次数,
为初始惯性权值,
迭代到最大进化数时的惯性权值。
为了方便更好的理解该算法,绘制了思维导图,如图10所示:
最终,得到预测结果如表6所示。

Table 6. Energy consumption forecast based on population forecast
表6. 基于人口预测的能源消费量预测结果
4.2. 模型评估
在模型评估中,可以选择以下几种方法:平均绝对误差(MAE) [17] 、平均绝对误差(MAE) [17] 、决定系数(R-squared) [18] 以及平均绝对百分比误差(MAPE)。本文选择MAPE (Mean Absolute Percentage Error, 平均绝对百分比误差)方法对模型进行评估,该方法有助于理解和比较预测结果与真实结果之间的平均偏差,更好地理解模型的表现和可靠性,并在业务决策中提供可靠的参考。具体而言,对于某一组样本数据,将计算其所有预测值与真实值之间的相对误差,然后取平均值并将其转换为百分比形式,即得到了该组数据的MAPE值。例如,如果MAPE为5,则表示该组数据的预测结果平均偏离真实结果的5%。通过计算不同数据组的MAPE值,本文可以比较不同模型在预测能力方面的优劣,并选择表现最佳的模型作为最终选择。
MAPE公式为:
(27)
利用给出的数据对2021~2060年的人口数据进行预测,得到预测结果,作为
,而将数据中的当年数据作为
。
最终,本文得到基于人口的能源消费量的四种模型模型的MAPE进行汇总得到结果如表7所示。

Table 7. Results of model evaluation
表7. 模型评估结果
通过单个模型及加权预测模型在人口总量的预测的精度对比,图11中可以看出,不同模型预测时的表现的具有一定的差异性,也存在个别异常时间点在单个模型预测中效果不佳。首先对3个模型的预测情况,线性回归模型的预测效果相对较弱,且对数据波动非常敏感。在对比XGBoost和LSTM的预测效果时,发现它们的预测结果相对接近,而且都具有较好的稳定性。具体来说,LSTM在预测精度方面表现更出色,但同时XGBoost模型的预测精度相对较差。因此本文结合3个不同的机器学习模型进行加权对最终结果进行预测,即保持了模型预测稳定的特点,同时也能提高模型的精度,组合模型保持了良好的预测精度,预测结果的精度对比单一模型有很大的提高。
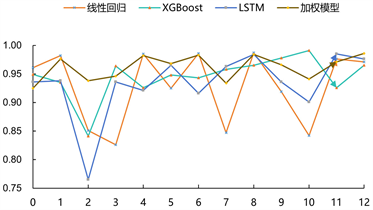
Figure 11. Comparison of the accuracy of different models
图11. 不同模型的精度对比图
4.3. 基于经济变化的能源消费预测模型
建立与上一节相同的线性回归预测模型,结果如表8。

Table 8. Linear regression model results
表8. 线性回归模型结果
注:***、**、*分别代表1%、5%、10%的显著性水平。
得到结果,如下所示:
(28)
根据关系式建立相同的预测模型,得到结果如表9所示。

Table 9. Forecast results of energy consumption based on economic changes
表9. 基于经济变化的能源消费量的预测结果
4.4. 区域碳排放量预测模型的建立
由于多元线性回归在区域碳排放量与人口、GDP和能源消费量之间的建模效果不理想,本文考虑使用岭回归作为一种改进方法。
岭回归(Ridge Regression)是一种线性回归的扩展方法,旨在应对线性回归中可能出现的多重共线性(multicollinearity)问题。多重共线性指的是在回归分析中,自变量之间存在高度相关性,这可能会导致模型的不稳定性和不准确性。在岭回归中,模型会保留所有的特征变了,但是会减小特征变量的系数值,让特征变量对预测结果的影响变小,岭回归 [19] 是通过改变其alpha参数来控制减小特征变量系数的程度。而这种通过保留全部特征变量,只是降低特征变量的系数值来避免过拟合的方法,称之为L2正则化。通过引入正则化项,岭回归的优化目标在于最小化损失函数。由于正则化项的存在,模型在估计系数时会更倾向于将它们缩小,从而减少多重共线性的影响。这有助于提高模型的稳定性和泛化性能。相比于普通线性回归,岭回归能够有效解决多元线性回归中的过拟合问题,并提高模型的稳定性和可靠性。通过压缩模型对特征的依赖程度,岭回归可以更准确地估计变量之间的关系,避免了模型对训练数据中的异常过度敏感的情况。
其目标函数为:
(29)
岭回归的主要优点是可以稳定模型的参数估计,减少参数估计的方差,从而提高模型的泛化性能。然而,与传统的线性回归相比,岭回归引入了正则化项,可能会导致参数估计的偏差增加。因此,在选择合适的正则化强度参数
时需要进行调参。
同样,区域碳排放量预测中采用岭回归模型 [19] [20] ,有望提高模型的预测精度和稳定性。
对于二范数的岭回归和优化函数,分别如公式(30)、(31)所示:
(30)
(31)
从最小二乘的角度来看,当特征之间存在高度相关性时,会导致矩阵的奇异性,进而使得无法求解回归系数。通过引入L2范数正则化项,也被称为岭回归,可以对模型的参数进行约束,使得矩阵保持可逆性。具体而言,L2范数正则化项的加入,会在目标函数中加入参数向量的平方和,并乘以一个调节参数
。这样,当
足够大时,正则化项的影响会压制原始的最小二乘解,从而使得矩阵能够满秩,即可逆。同时有效减小过拟合的风险,提高了模型的鲁棒性和泛化能力。所涉及公式如下所示:
(32)
利用SPSSPRO进行求解,并利用SPSSPRO绘制了岭迹图如图12所示。同时,模型的拟合优度R²为0.983,模型表现为较为优秀。
建立得到,碳排放量与人口、GDP和能源消费量预测相关联关系式为:
(33)
最终,根据关联式采用加权预测模型,得到结果如表10所示。
5. 结论
本文结合实际背景,考虑了现实世界中各种复杂的因素和不确定性,包括建立数学模型、数据预处理、多种模型预测方法的比较和分析、情景设计、路径规划等多个方面,成功地解决了碳达峰和碳中和目标相关的复杂问题,为推进碳减排和促进可持续发展做出了重要贡献。本文不仅使用了多元线性回归模型,还引入了LSTM、XGboost等多种方法,以提高预测精度,并采用加权平均的方法综合考虑各模型的结果,这有助于减小预测值与真实值之间的误差。总而言之,本文考虑了问题的多个方面,采用了多种方法和技术,以全面、系统地解决问题。