1. 引言
压电陶瓷是一种可以将机械能和电能相互转换的材料,由于其轻型、成本低和能量转换效率高的优点,被广泛应用于能源(超声化学和超声采油等)、环保(超声清洗和污水处理等)、机械(超声加工和超声焊接等)、医疗(超声热疗和高强度聚焦超声治疗等)等领域 [1] [2] 。在压电陶瓷的应用中,机械品质因数Qm是评价能量损耗的重要参数 [3] 。Qm的本质为一个周期内总储存的能量和损失的能量之比。为了计算Qm的值,传统有两种方法:一种是定义式法,从机械品质因数的定义出发,利用阻抗曲线得到压电陶瓷的谐振和反谐振频率、最小阻抗和自由电容等数据进行计算 [4] ;另一种方法是3 dB法,3 dB法只需要从阻抗曲线中读出压电陶瓷的谐振频率和半功率带宽就可以计算Qm [5] [6] 。
传统机械品质因数Qm的测量方法通常是在电场强度为1 V/mm或更小的电场下利用阻抗分析仪测试得到。但是,大多数压电陶瓷的工作电场远远大于1 V/mm,如超声波换能器的工作电压有可能达到1000 V以上。由于压电材料的非线性特性,在弱场下测得的Qm值不足以评价压电陶瓷的真实工作性能 [7] 。为了得到压电陶瓷的强场Qm值,且避免强场下材料的自发热特性,K.Uchino教授等提出一种新型的测试方法,即脉冲驱动法 [3] 。该方法通过给压电振子施加一定循环数的电压脉冲,短路后利用压电振子电流衰减曲线计算得到机械品质因数。以往的瞬态法研究通过测量电流衰减曲线两个不同时刻的电流幅值计算Qm值,由于电流噪声的影响,该方法存在误差较大和重复性差的问题。
为了提高测量准确性,在本文中我们提出通过拟合衰减曲线衰减系数的方法得到Qm值,能显著减小测量误差。同时,本文基于虚拟仪器LabVIEW设计了一种测量大功率下压电陶瓷机械品质因数的软硬件系统,该系统可以实现激励信号的生成、数据采集、信号处理并实时计算Qm值的功能。整个测量过程在LabVIEW环境中完成,能提高测量效率,满足实验需求。
2. 脉冲驱动法原理
脉冲驱动法(瞬态法)是指通过对压电陶瓷施加Tone-Burst脉冲 [8] ,测量其瞬态振动从而得到压电陶瓷强场下Qm值的方法。这种对瞬态振动的实时监测在数学上等同于通过傅里叶变换使用共振/反共振技术的频域测量 [9] 。瞬态法的具体步骤为:在压电陶瓷两端施加n次循环的交流电压脉冲
,直到振动速度上升到足够的振幅,即其振动达到稳态。这里,U0是驱动电压的幅值,ω是压电陶瓷该驱动电压下的共振角频率。接着,将压电陶瓷的电端短路从而得到电流的瞬态衰减曲线。图1为脉冲驱动法下压电陶瓷的电压、电流和振动速度波形。
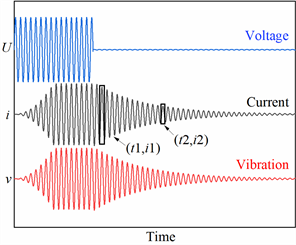
Figure 1. Schematic diagram of the waveform of the transient method
图1. 瞬态法波形示意图
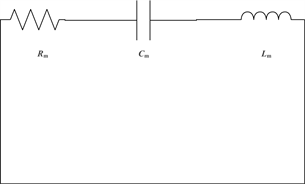
Figure 2. Equivalent circuit when piezoelectric ceramic resonates
图2. 压电陶瓷谐振时等效电路
压电陶瓷谐振短路时的等效电路如图2所示,与RLC电路谐振特性相似。根据基尔霍夫第二定律,可以得到压电陶瓷谐振时的电流电压关系:
(1)
其中,
是等效电感,
是等效电容,
是等效电阻。
对式(1)进行微分处理,整理可得:
(2)
其中,
求解式(2),可得到电流表达式:
(3)
式中,
为压电振子短路时电容和电感储存的电荷量。从
的表达式可以看出,谐振短路时压电陶瓷的电流幅值变化曲线为指数衰减的正弦曲线。谐振时,压电振子的振动速度和电流呈正比,因此瞬态法中压电振子的振动速度变化曲线也为指数衰减的正弦曲线 [10] 。实验中测得的电压电流变化曲线如图3所示,由图可知施加电压后,压电振子将达到稳定振动;将电源短路后,压电振子的电流曲线存在衰减阶段。根据电流的衰减曲线,提取其包络线可以拟合得到电流衰减系数
。

Figure 3. (a) Voltage and (b) current variation curves of piezoelectric ceramics
图3. 压电陶瓷(a) 电压和(b) 电流变化曲线
通过等效类比的方法,RLC振荡电路的电学量和阻尼弹簧振动模型的力学量可以建立一定的联系 [11] 。阻尼弹簧模型中,阻力在一个振动周期做功为W1:
(4)
其中,
,将阻力公式代入式(4):
(5)
弹簧振子在一个周期内的平均动能为:
(6)
将式(5)用式(6)表示:
(7)
在弱阻尼振动中,一个周期内的平均动能等于平均势能 [12] 。在一个谐振周期内,储存的能量为平均动能和平均势能之和,损耗的能量为阻力做功。那么根据机械品质因数Qm的定义式可得:
(8)
3. 系统设计和功能实现
3.1. 硬件构成
为了实现压电陶瓷强场机械品质因数的测量,本文设计了基于LabVIEW的瞬态法测量系统,示意图如图4所示。该系统主要由LabVIEW程序、任意波形信号发生器(Rigol DG5072)、功率放大器(NF HSA4011)和示波器(Rigol MS05074)、高压探头(PINTECH DP-25)、电流探头(TEK A6302)和激光测振仪(Polytec OFV-505)组成。首先,由LabVIEW程序控制信号发生器脉冲信号的参数并产生Tone-Burst脉冲信号,再由功率放大器将生成的脉冲信号放大,加载到待测压电陶瓷上;然后,由示波器读取通过高压探头和电流探头测量得到的压电陶瓷的电压和电流值,并将采集的电压电流信号传输到LabVIEW中进行数据处理。同时,利用激光测振仪测量压电振子达到稳态时的边界振动速度以表征不同振动速度时压电振子的Qm值。
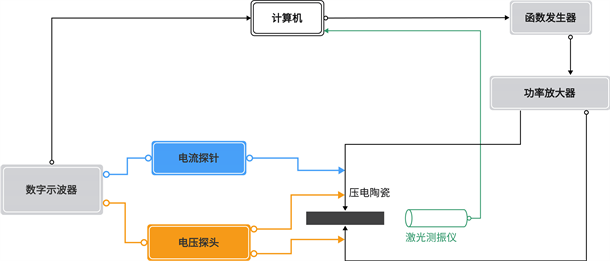
Figure 4. Schematic diagram of piezoelectric ceramic strong field Qmmeasurement system
图4. 压电陶瓷强场Qm测量系统示意图
3.2. 软件设计
在20世纪80年代,美国NI公司提出了虚拟仪器技术,该技术利用软件设计将计算机与实验仪器相连接,通过I/O接口实现计算机对实验仪器的参数设置和数据采集 [13] [14] 。本文中开发的测量系统基于LabVIEW 2020平台,主要由四个部分组成,分别为函数发生器参数设置与信号产生、示波器波形采集与处理、频率自动跟踪和机械品质因数计算。软件开发主要分为前面板和后面板两部分,前面板是仪器操作界面,后面板则是具体的程序编写界面。
前面板主要分为仪器连接、示波器参数输入、函数发生器脉冲信号参数输入和示波器波形读取及处理四个方面。函数发生器脉冲信号的参数设定,主要包括频率、电压、脉冲驱动中的波形循环数和脉冲周期设定;而示波器参数输入,包括读取示波器的通道选择和低通滤波的设置。程序运行流程为:首先计算机向函数发生器发送命令检测通信是否正常;其次,若通信正常后,则将设定的相关参数写入函数发生器产生波形信号;然后,示波器读取电流信号并传输到计算机,计算机检测此时是否为谐振频率:若为谐振频率,结束电压驱动,处理读取的电流信号并计算机械品质因数值;若不是,则改变频率参数,再次写入函数发生器产生波形信号。图5为测量过程的软件流程图。
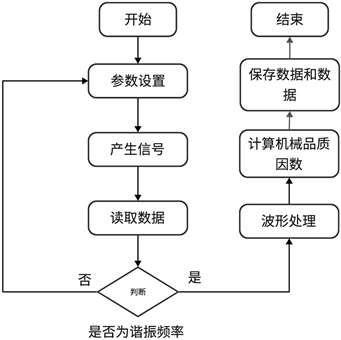
Figure 5. Software flow chart of measurement process
图5. 测量过程软件流程图
压电振子的阻抗谱会随着驱动电场的增加而发生畸变,且其谐振频率和反谐振频率大幅降低 [15] 。这是因为压电材料在强场驱动下表现出的非线性弹性特性 [16] [17] 。为了寻找强场下的谐振频率,一般需要调节脉冲信号的频率,并观察示波器上的电流幅值。根据压电陶瓷的阻抗特性,当电压恒定时,电流最大时的频率近似等于其谐振频率。为了简化寻找谐振频率过程,设计自动化的频率跟踪程序非常必要。本文的测量系统采用以下方法进行频率跟踪:首先设定一个起始频率和频率步长,将参数设定和信号采集的程序置于While循环中,然后通过寄存器将上一个频率下的起振完全的电流幅值I1保存,并将下一个频率下的电流幅值I2与其进行比较。若频率向下扫描,则通过判断I1 < I2,确定I2对应的频率为谐振频率。
为了得到压电陶瓷的机械品质因数Qm,需对得到的电流数据做滤波和提取包络线提取等相应的数学处理。按照传统的处理方法,通常需要将电流数据导入Origin和Matlab等软件中进一步分析,该方法不能实时处理数据,操作效率低。本文通过调用LabVIEW中的信号处理和数学分析模块,实现测量数据的实时处理和分析。本文数据处理的基本步骤为:首先,将得到的电流数据通过低a通滤波程序去除噪声;之后,提取滤波后电流信号的包络线,即得到电流的幅值变化曲线;其次,找到电流衰减的起始点,截取需要的电流衰减曲线;最后,将得到的电流衰减曲线导入拟合程序得到电流衰减系数
,根据衰减系数
和谐振频率就可以求得机械品质因数Qm。
4. 测量结果和分析
在本文实验中,采用尺寸为45 mm (外径) × 20 mm (内径) × 6 mm (高)的PZT-8圆环压电振子和20 mm (长) × 6 mm (宽) × 2 mm (高)的PZT-5长条压电振子作为实验样品,测量其在不同驱动电压和振动速度下的Qm值,测量过程如图6所示。由6可知,测量系统可以得到理想的电流衰减曲线,并且自动拟合出相应的Qm值。为了测试本系统数据处理结果的准确性,将LabVIEW计算结果与Origin软件处理得到的结果进行了比较分析。
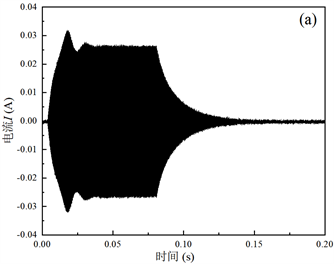
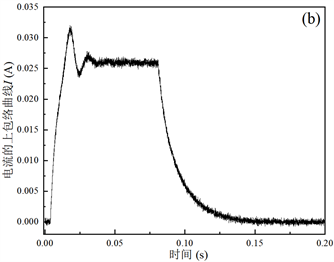
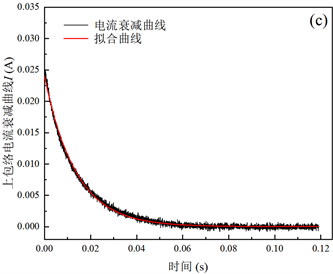
Figure 6. Piezoelectric vibrator in strong fields change curve in the process of Qm measurement: (a) current curve after filtering; (b) upper envelope of the current; (c) Attenuation coefficient fitting of upper envelope attenuation curve
图6. 压电振子在强场下的Qm测量过程中的变化曲线:(a) 滤波后的电流曲线;(b) 电流的上包络线;(c) 上包络衰减曲线衰减系数拟合

Figure 7. PZT-8 circle of piezoelectric vibrator Qm value with voltage (a) and (b) curve of vibration velocity change
图7. PZT-8圆环压电振子的Qm值随(a)电压和(b)振动速度变化的曲线
图7为PZT-8压电圆环的Qm随电压变化和振动速度变化的曲线。由图可见,随着电压和振动速度的增大,PZT-8圆环压电振子的机械品质因数急剧减小。这是由于当加在样品两端电压的增大,一方面畴壁运动的能量增强,内摩擦增大使得机械品质数变小;另一方面,随着振动速度的增加,压电材料的介电损耗也会增加,由于介电损耗与机械品质因数成反比,导致机械品质因数进一步减小 [16] 。从结果中也可以发现,由LabVIEW测量系统得到的Qm值与Origin软件拟合得到的Qm值符合较好,两种计算方法的最大误差为3.48%,进一步验证了LabVIEW测量系统的可靠性,满足了压电陶瓷强场Qm值实时测量的需要。
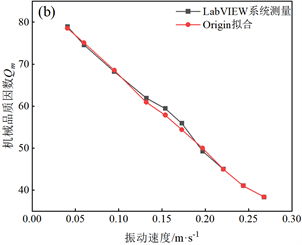
Figure 8. Piezoelectric ceramic PZT-5 strip of Qm with voltage (a) and (b) the curve of vibration velocity
图8. PZT-5长条压电陶瓷的Qm随(a)电压和(b)振动速度变化曲线
此外,由图8可知PZT-5长条压电振子的Qm值随电压和振动速度的变化规律与PZT-8圆环压电振子的较为相似。随着电压和振动速度的增大,PZT-5长条的机械品质因数也快速下降。不同之处在于,在相同的电场和振动速度条件下,PZT-5压电振子的Qm值远小于PZT-8压电振子的Qm值,其原因在于PZT-5压电陶瓷的畴壁比PZT-8的更容易运动,从而导致其PZT-5材料的内摩擦更大,机械品质因数更小。
5. 结论
本文基于LabVIEW软件提出了一种压电陶瓷强场机械品质因数测量的数据处理方法和测量系统。该系统能够控制函数发生器生成脉冲信号,采集压电振子短路条件下的衰减电流波形数据,并通过系统对数据采取滤波、包络线提取和电流衰减系数拟合等操作,从而准确实时地测量出强场下压电陶瓷的机械品质因数。实验结果表明,本文开发的压电振子强场机械品质因数测量系统具有很好的准确度(误差为5%以下)、稳定性和使用便捷性;同时,从实验结果可知在同一电压下,PZT-5压电振子的机械品质因数远小于与PZT-8压电振子,且两种压电振子的机械品质因数都随驱动电压的增大和随振动速度的增大而减小。本文开发的压电振子强场机械品质因数测量系统为全面表征强场下压电振子性能奠定了一定的实验基础。