1. 引言
我国机场跑道主要采用水泥混凝土道面结构,因其稳定性、维护费用低和环保特性而被广泛采用。然而,在使用一段时间后,许多水泥混凝土道面出现了各种病害,例如接缝破碎、填缝料损坏、板体断裂和坑洞,这些问题严重影响了道面的使用寿命,对机场的运行安全造成了显著威胁。当前的机场跑道水泥混凝土道面板的装配方法一般在地基沉降稳定后进行,但高填方地基不均匀沉降会导致道面板在外力作用下产生应力集中现象,这可能导致板边角的局部破坏,进而缩短道面板的使用寿命。
国内外学者对高填方地基上加盖水泥混凝土道面板的层底应力进行了广泛的研究。杨彪 [1] 模拟了道面面层和接缝用板单元,并考虑了面层和基层之间的界面接触,构建地基–道面–飞机轮载的三维有限元模型;李一凡 [2] 构建了水泥混凝土道面板的有限元模型,对板内最大弯拉应力随脱空状态的变化规律进行了分析;江圣泽 [3] 使用有限元软件针对水泥混凝土板块的受力进行模拟分析,研究发现板边和板角的应力最大,机轮滑行过程中,接缝两侧部位产生挤压现象;国外学者Alexander John [4] 基于有限元建模,采用了考虑弯剪耦合的非线性梁单元对水泥混凝土板进行建模。可以看出,国外研究大多集中在理论分析和数值模拟方面,对于实际道面的影响机理及解决方案的落地应用存在一定差距;国内研究多侧重于飞机动静荷载引起的道面板损坏研究,缺乏对加盖道面后,受地基影响的层底应力变化规律研究。
因此本研究通过理论分析和有限元仿真相结合的方法,构建了不同填方高度下30 m、40 m、50 m、60 m、70 m、80 m、90 m的加盖道面板的高填方模型,分析了不同填方高度对道面板的层底拉压应力的影响规律,以期为解决实际道面破损问题提供更为科学和全面的参考依据。
2. 有限元模型建立
2.1. 有限元基本理论
在本研究中,我们选择采用有限元法进行道面板应力应变数值模拟分析,并选用特定的有限元分析软件来进行数值计算。我们采用了CPE4和CPE4P平面应变单元,其中CPE4平面应变单元用于考虑平面应变问题,适用于分析机场道面板在水平方向上的变形。CPE4P平面应变单元与CPE4单元类似,也用于平面应变问题,但它具有更高的数值稳定性,特别适用于模拟具有非线性行为的土体和填筑材料。其他所涉及到相关的有限元基本方程式如下文介绍。
(1) 位移函数与坐标变换
在有限元分析方法中引入等参元概念,将整体坐标中的子单元转化成自然坐标下(ξ、η坐标)的任意母单元,四节点等参单元如图1所示。
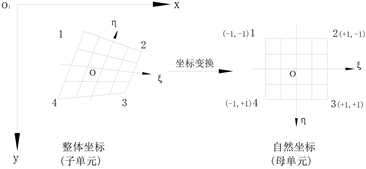
Figure 1. Four-node isoparametric element
图1. 四节点等参单元
母单元在自然坐标系(ξoη)下为正方形,则位移函数
在参考四节点矩形单元的位移函数后,可取为:
(1)
(2) 单元应变矩阵和应力矩阵
单元应变{ε}可以由位移函数式(1)代入平面问题的几何方程而得到:
(2)
(3)
(3) 单元刚度矩阵
平面问题的刚度矩阵定义为:
(4)
应变矩阵[B]由于是局部坐标
的函数,面积元dA = dxdy必须用局部坐标
表示,则可以证明:
(5)
2.2. 数值仿真模型构建
本节针对某机场工程不同填方高度的填筑体,填筑土体参数参考施工现场勘察资料,引入道面层,探究机场高填方工程道面板层底应力的变化。考虑到在进行有限元软件建模时,边界尺寸会对计算结果造成比较大的影响,参考国内外学者的研究,高填方的坡脚到边界的尺寸不应小于填筑体高度的1.5倍,高填方顶部至边界的距离不应小于填筑体高度的1.0倍,即可消除边界效应对计算精度造成的影响,基于以上的研究结果,建立如图2所示的几何模型。
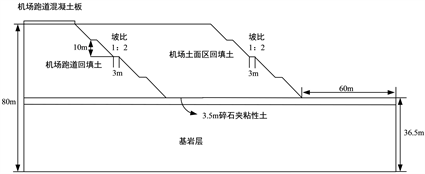
Figure 2. High fill geometric model of overlay pavement
图2. 加盖道面的高填方几何模型
道面层参数的确定主要依据了浙江大学赵云博士的研究成果 [5] 以及民航专业工程项目的实践经验,道面板的参数如表1所示。

Table 1. The value of pavement panel parameters
表1. 道面板参数取值
为了探究不同填方高度下对道面板的力学特征,本节分别对不同填高模型30 m、40 m、50 m、60 m、70 m、80 m、90 m引入道面层,分析其层底应力S11,以此来研究不同填方高度对道面板的影响。图3为不同填方高度30 m、40 m、50 m、60 m、70 m、80 m、90 m下,层底应力随跑道距离变化的云图。
3. 仿真模拟分析
基于建立的加盖道面的高填方有限元模型,将道面板从应力应变中提取出来,在不同填方高度(30 m、40 m、50 m、60 m、70 m、80 m、90 m)下,距离跑道中心点越近的区域呈现出更深的颜色,表示层底拉应力更为显著;而距离跑道中心点越远的区域则显示出浅色,表明层底拉应力逐渐减小,直至在距离11 m至20 m的范围内转变为层底压应力,并逐渐增大。
为了更直观地探究不同填方高度下道面板层底应力的变化情况,我们提取了道面板底部的路径数据,并绘制了层底应力变化趋势对比图,如图4所示。在这个图表中,层底应力S11呈现正数时代表层底为拉应力,而当S11为负数时,则表示层底为压应力。
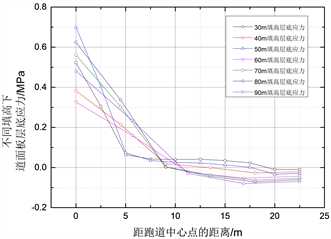
Figure 4. Comparison of stress change trends at the bottom of different fill heights
图4. 不同填方高度下层底应力变化趋势对比图
不同填高下的7条曲线,随着距跑道中心点距离的增大,道面板层底应力的变化趋势均是从大到小、由正变负,其层底应力的表现形式从层底拉应力逐渐减小成为层底压应力。其中道面板中心点处的最大拉应力为0.7 MPa,最小拉应力为0.3 MPa;在道面板最右侧处的最大压应力为0.06 MPa,最小压应力为0.02 MPa。随着填筑高度不断增加,水泥混凝土板底应力均先快速减小再趋于平缓,且以距跑道中心点10 m的距离为明显分界点,这种基本的层底应力趋势与河南大学张业 [6] 学者针对装配式水泥混凝土路面结构的性能研究较为相符,可以推断,本研究构建的加盖道面板的高填方模型具有可行性。
4. 结论
本文结合某机场高填方工程施工项目,采用有限元软件建立不同填方高度的加盖道面的高填方模型进行数值模拟计算,对不同填方高度对道面板层底拉压应力的影响进行分析,得出以下结论:
(1) 通过理论研究及施工现场设计勘察资料,构建了不同填方高度30 m、40 m、50 m、60 m、70 m、80 m、90 m的加盖道面板的高填方模型,并采用了CPE4和CPE4P平面应变单元,模拟了不同填高对道面板层底应力的分布规律,此建模思路可为机场高填方沉降模拟仿真提供指导。
(2) 通过有限元计算分析,得到不同填方高度30 m、40 m、50 m、60 m、70 m、80 m、90 m的水泥混凝土道面板的层底应力大小,得到距离跑道中心点越近的区域层底拉应力更为显著;而距离跑道中心点越远的区域层底拉应力逐渐减小,直至在距离11 m至20 m的范围内转变为层底压应力,并逐渐增大。
(3) 50 m填方高度下,道面板中心点处的最大拉应力为0.7 MPa,60 m填方高度下,最小拉应力为0.3 MPa;在90 m填方高度下,在道面板最右侧处的最大压应力为0.06 MPa,填方高度30 m下,最小压应力为0.02 MPa。