1. 引言
近些年来,量子信息科技的进步不仅对量子物理理论和信息科学,而且对量子技术的发展产生了巨大影响。研究发现,量子现象特别是量子关联(包括量子纠缠、量子相干以及量子失协)具有使量子器件的性能远超相应经典器件的作用 [1] ,由此对量子电池的研究应运而生 [2] [3] 。
众所周知,传统电池是一种储能由外界提供,并且可以为外部设备提供动力的电化学装置。随着使用设备的不断小型化,某些特定情况下电池单元也需要做的越来越小。因此,当电池单元接近分子和原子大小时,描述它们的作用就必须考虑量子效应 [4] 。这促使人们在量子热力学的框架下做出对量子电池的研究 [5] 。简单地说,量子电池实际上是一个有效地储存能量并对外做功的量子力学系统。目前对量子电池的研究主要集中在三个方面:首先是量子电池的最大储能问题;其次是最小充电时间或量子电池的功率问题;再者是关于能量的提取,即对外做功问题。无论关于哪方面,量子信息理论和技术研究发现,量子纠缠、相干以及其它量子关联等量子效应的存在,原则上都可以使量子电池系统的性能远超或者改变经典条件下相应的电池设备 [6] [7] [8] 。研究人员已经提出了一些可能实现量子电池的实验方案,如自旋链、耦合于腔中的纳米结构量子点以及超导量子比特。然而实际实施这些技术任务,仍有大量的理论问题需要解决。特别地,量子纠缠仍然是其中重要的研究课题。
十年前,Alicki和Fannes首先讨论了纠缠的产生和存在对从多单元量子电池系统提取最大功的影响 [2] 。他们表明,对于n个相同的量子电池系统,非局域幺正操作以及在此操作下系统所获得的纠缠,相对于局域操作可以增加功的提取量。不久之后Hovhannisyan等人在发表于物理学期刊《物理评论快报》上的一篇文章中指出,非局域操作不产生纠缠也能提取最大功 [9] 。也就是说,存在某种情况,尽管在操作过程中系统一直处于分离态,也可以提取最大的功。或者说,纠缠(作为一种“源”)不是提取最大功的基本成份。不过,其后的多个研究小组的研究人员指出,虽然提取最大功不一定需要纠缠,但是量子关联(特别是量子纠缠),仍有可能在量子电池充放电等诸多性能方面起重要作用 [10] [11] [12] [13] [14] 。另外,文献 [3] 的作者研究指出,多单元量子电池系统存在着集体量子优势,即n个存在相互关联的量子电池的充电功率具有比n个独立量子电池充电功率大的特性。这个特性甚至对处于混合态的量子电池系统也成立。文中尽管没有表明这种集体效应的性质,但是量子纠缠在其中所起的作用是肯定的。再者,有学者还利用两能级量子系统构成的系综,研究了存在相互关联的多单元量子电池的寿命问题,得出了有意义的结果 [14] 。尽管量子关联,特别是量子纠缠已经受到多方关注,但是人们对量子关联在量子电池性能方面所起的作用仍然存在争议 [15] [16] 。在文献 [17] 中作者通过分析两量子比特组成的电池系统的所谓局域“钝态”(passive state)即利用局域幺正操作不可能从中提取能量的状态),发现了状态纠缠量与通过整体操作提取功的这个状态能量之间存在的关系。并且最近,人们也探讨了钝态与量子电池充放电能力的关系 [18] ,给出了供进一步研究的开放成果。文献 [19] 的作者,则对量子电池在带有负载时的情况下提取功的问题做了有益的探讨,结果肯定了量子关联在提取功中的作用。最近有学者研究了带有多个相同辅助系统的量子电池在耗散过程中的充放电问题 [20] ,结果表明量子电池完全可以进行有效地工作。除了利用量子关联优化量子电池性能之外,近两年有学者提出了一种可以不从热源而是直接从量子测量过程中获得能量对外做功的方法 [21] [22] 。
在这篇文章中,为了深入探讨量子纠缠的作用,我们将通过一个具体模型表明,当充电器和量子电池初始状态存在纠缠时,量子电池的充放电会受到怎样的影响。
2. 量子电池理论
一般来说,量子电池可以由一个封闭量子系统构成。设它由一个哈密顿量为H0的d维量子系统组成
(1)
这里,非简并能级为εj < εj + 1。其特例是一个两能级粒子系统构成的量子电池。其中存在一个与时间相关的场V(t) (0 ≤ t ≤ τ)被用来可逆的、并通过H0 + V(t)生成的幺正演化算符从这个电池提取能量。假设电池处于密度矩阵为ρ的初始态,系统的演化由薛定谔方程决定(
)
(2)
这里可知,ρ(0) = ρ,方程的解可以表示为
(3)
其中,幺正演化算符U(t)为
(4)
式中T是时序算符。经过时间τ之后,提取的功为
(5)
通常人们更想知道的是由电池中可提取的最大量的功,这个功称作“ergotropy”,可以表示为
(6)
若设σ是无法提取功的态,这样的态既是钝态 [23] ,则有
(7)
其中(7)式要求对所有幺正变换U成立。等价地,当且仅当
(8)
也就是当且仅当σ与H0对易,则σ是钝态。从定义容易看到,对于任何给定的状态ρ,都有唯一的一个钝态σρ。这个态可由ρ的幺正旋转Uρ得到
(9)
其中,{rj}是ρ的并且按非增加序排列的本征值。相应的最小能量为
(10)
因此,我们可以得到下列最大功的著名表达式 [23]
(11)
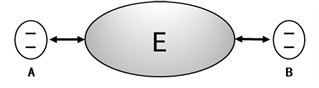
Figure 1. Schematic representation of the model analyzed in this work
图1. 本文中的模型系统草图
3. 模型及计算结果与分析
为了研究问题具体起见,受文献 [24] 启发,我们考虑一个模型,其由三部分构成:量子充电器A,量子电池B,以及在A和B间作为媒介的它们共同的环境E (见图1)。这个模型实际上是目前常用的无线充电装置的简化的量子化形式。不失一般性,假设充电器和量子电池皆为2-量子比特系统,且具有激发态
和基态
,并设激发态和基态转换频率相同为
。它们都置于真空态的零温单模玻色子场中,这个模型系统的哈密顿量在旋波近似下可以表示为(以下令
)
(12)
其中,自由哈密顿量H0为
(13)
这里,v为光子的跃迁频率,
分别为相应原子的反转算符,a†和a为光场的产生算符和湮灭算符。方程(12)右面第二项描述的是系统和场的相互作用,其中
(14)
g为原子与腔场间的耦合常数,
、
分别为相应原子的下降算符、上升算符。在相互作用绘景下,哈密顿量(12)化为
其中,自由哈密顿量H0为
(13)
这里,v为光子的跃迁频率,
分别为相应原子的反转算符,a†和a为光场的产生算符和湮灭算符。方程(12)右面第二项描述的是系统和场的相互作用,其中
(14)
g为原子与腔场间的耦合常数,
、
分别为相应原子的下降算符、上升算符。在相互作用绘景下,哈密顿量(12)化为
(15)
其中
。上述方程中的f(t)是无量纲函数,对于
它等于1,其他时间为0。其被用于相互作用的开关,τ代表充电时间。假设t < 0时,充电器和量子电池各自孤立,且不与环境作用。在t = 0时刻,通过开启HAE和HBE使A与E联系并且B与E联系。在此方案中A和B彼此没有相互作用仅有信息关联。由于
并且t = 0时环境处于基态,因此量子电池最终的能量不仅源于充电器而且有可能源于相互作用开、关转换时的热力学功 [25] [26] 。由此可知,在相互作用时间
内,仅充电器的一部分能量通过环境媒介流向了量子电池。最后,在τ时刻,充电器A和量子电池B断开了与环境E的连接,再次处于孤立状态。
本文考虑的模型,充电器与量子电池没有直接相互作用,实际上是一种无线充电过程,环境只是起到了媒介的作用。这里我们感兴趣的是充电器A和量子电池B初始的纠缠态对充、放电的影响。因此,我们选择整个系统的初态为
(16)
其中
为库的真空态,并且当时θ = 0,上式表明量子电池初始处于能量为0的空态同时充电器处于能量最大状态,此时电池与充电器处在纠缠度为0的非纠缠态。对于θ = π/4,则量子电池与充电器初始处在纠缠度为1的最大纠缠态 [1] 。由上述假设,t时刻的态矢可以表示为
(17)
将(15)和(17)式代入薛定额方程
(18)
可以解得(由初始条件知c3(0) = (0))
(19a)
(19b)
由式(17)写出的密度算符可以求得τ时刻充电器和量子电池的约化密度算符分别为
(20a)
(20b)
利用约化密度算符(20a)和(20b),求得充电器和量子电池的内能分别为
(21a)
(21b)
进一步可以求得充电过程结束时充电器失去的能量和量子电池获得的能量分别为
(22a)
(22b)
在图2中,我们作出了
对于无量纲时间gτ的动力学过程(图中取的是共振情况Δ = 0,画出了
以及
对于gτ的函数曲线)。图中画出了几种充电器与量子电池不同初始纠缠态时ΔE(τ)的时间演化曲线。首先看到,无论哪种情况演化都是周期性振荡曲线,这是由于我们选用的模型是理想化的模型造成的,并且可以看到由于这个理想模型的选取,充电器中的电完全被量子电池所吸收。不过,选取这种简单模型并不影响我们要研究问题的本质,即纠缠对充放电的影响。其次我们看到最重要的是,当充电器与量子电池初始纠缠度最大时(
),充电器传送到量子电池的能量最大。这一点由图3更清楚的看到。在图3中,(a)描述的是充电器传送的能量,(b)是量子电池接受的能量,可以看到两者能量在任何情况下都是等量的,这与图2描述的是一致的。下面我们研究最大功的动力学行为。
 (a) (b) (c)
(a) (b) (c)
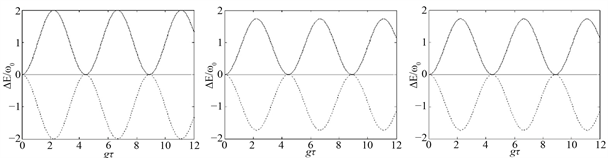
Figure 2. Dynamical dependence of ΔE(τ)/ω0 as a function of the dimensionless quantity gτ. The dot line describes the relationship between ΔEA(τ)/ω0 and gτ; The solid line describes ΔEB(τ)/ω0 in relation to gτ. Initial state of system are as follows:
. Here: (a) θ =π/4,(b) θ = π/3,(c) θ = π/6
图2. ΔE(τ)/ω0作为无量纲量gτ的函数的动力学依赖关系。点线描述的是ΔEA(τ)/ω0与gτ的的关系;实线描述的是ΔEB(τ)/ω0与gτ的关系。系统的初态为:
。这里取:(a) θ =π/4,(b) θ = π/3,(c) θ = π/6
 (a) (b)
(a) (b)
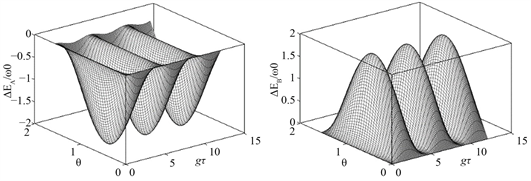
Figure 3. ΔE(τ)/w0 as a function of the dimensionless quantity gτ and the parameter θ. Initial state of system are as follows:
. (a) The ΔEA(τ)/w0 function of charger A, (b) The ΔEB(τ)/w0 function of of quantum battery B
图3. ΔE(τ)/w0作为无量纲量gτ and参数θ的函数关系。系统的初态为:
。(a) 充电器A的ΔEA(τ)/w0的函数关系,(b) 量子电池B的ΔEB(τ)/w0的函数关系。
利用(11)式,得到最大功为
(23)
其中容易获知
(24)
量子电池最大功W/Wmax作为无量纲量gτ的函数的时间演化曲线被画在图4中。系统的初态为:
。图中,实线对应于θ = π/4,即充电器和量子电池初始处于最大纠缠态;点画线对应于θ = π/3,所对应的纠缠态次之;点线对应于θ = π/8,相应的纠缠态为其中最小。容易看到W/Wmax是周期性变化的。重要的是我们看到,充电器和量子电池的纠缠仍然对这个最大功起决定作用。最大纠缠时(θ = π/4),量子电池的最大功最大;纠缠度小时(θ = π/3和θ = π/8)这个最大功变小。因此,要想使量子电池输出更大的功,就应使充电器和量子电池处于纠缠度相对大的状态。
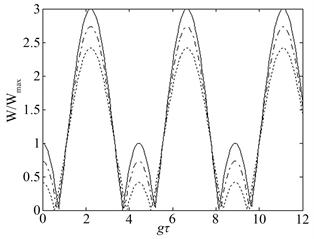
Figure 4. Dynamical dependence of W/Wmax as a function of dimensionless quantity gτ. Initial state of system are as follows:
.The solid line corresponds to the θ = π/4, dot-dashed line corresponds to the θ = π/3, the dotted line corresponds to the θ = π/8
图4. W/Wmax作为无量纲量gτ的函数的动力学依赖关系。系统的初态为:
。其中实线对应于θ = π/4,点画线对应于θ = π/3,点线对应于θ = π/8
4. 结论与总结
在这篇文章中,我们研究了充电器与量子电池初始处于纠缠态时,系统充放电能量以及量子电池最大功的演化过程。我们的理论结果表明,纠缠态对充放电及量子电池最大输出功起重要的积极作用。纠缠最大时,充电器和量子电池充放电最大,并且量子电池最大功也最大。随着充电器和量子电池纠缠度的减小,充放电和量子电池最大功也变小。尽管上述结果的得出是在我们选取的理想模型下获得的,但是,由于这个电池充放电系统是典型的量子电池系统,因此这些结论具有普遍性,对量子电池的研究有及其重要的指导意义。在今后的研究中,我们将在更实际的耗散环境下进一步对这个问题进行探讨。我们相信量子关联(特别是量子纠缠)对量子电池的性质一定有积极的作用。
参考文献
NOTES
*通讯作者。