基于多目标蛇优化算法的非侵入式负荷监测研究

Research on Non-Invasive Load Monitoring Based on Multi-Objective Snake Optimization Algorithm

摘要: 随着经济社会的发展和节能环保的要求，负荷监测已成为一个研究重点，安装简单、经济安全的非侵入式负荷监测(Non-Intrusive Load Monitoring, NILM)更是成为近年研究的热门领域。该文针对NILM研究中存在的负荷分解准确率不高及实际应用所需时间较长的问题，通过将有功功率与稳态电流作为识别特征，引入了由Fatma A. Hashim和Abdelazim G. Hussien于2022年提出的多目标蛇优化算法(Multiple Objective Snake Optimizer, MOSO)并建立数学模型，经过选取家中最常见的电器进行实验测量并分析，得出该方法有效提升了负荷分解的准确率并大大缩减了实验时间的结论。通过与不同算法在同一数据上进行实验分析并对比实验结果，验证了该文算法在准确率及实验效率上有明显提升，证明了该文算法具有优越性。

Abstract: With the development of the economy and society and the requirements of energy conservation and environmental protection, load monitoring has become a research focus, and non-intrusive load monitoring (NILM) that is simple to install, economical and safe has become a hot field in recent re-search. This article addresses the issues of low accuracy in load decomposition and long practical application time in traditional non-invasive load monitoring algorithms in NILM research. By using active power and steady-state current as identification features, the Multi-Objective Snake Opti-mizer (MOSO) algorithm proposed by Fatma A. Hashim and Abdelazim G. Hussien in 2022 is intro-duced and a mathematical model is established. After selecting the most common electrical appli-ances in the home for experimental measurement and analysis, it was concluded that this method effectively improves the accuracy of load decomposition and greatly reduces experimental time. By conducting experimental analysis on the same data with different algorithms and comparing the experimental results, it was verified that the proposed algorithm has significant improvements in accuracy and experimental efficiency, proving its superiority.

1. 引言

近年来，随着智能电网的发展和人工智能技术在家庭中的应用，通过开展对用户用电模式的分析，深入挖掘用户用电节能的潜力，减少家庭电费的同时实现电网电量的削峰填谷，促进区域内电网地安全稳定运行已成为目前新的科研发展趋势。为了建立一个高效的能源管理系统来评估用户的电能消耗和使用习惯，负荷监测已经成为了目前的一个研究热点。根据监测传感器的安装方式，负荷监测一般可分为侵入式负载监测(Intrusive Load Monitoring, ILM)和非侵入式负载监测(Non-Intrusive Load Monitoring, NILM) [1] 。ILM需要在每个电器上安装一个或多个传感器来获取其工作状态信息，这不仅成本高，而且可能对用户的隐私造成威胁。相比之下，NILM只需要在主电源入口安装一个传感器就可以获取不同电器的总功耗，通过智能算法将采集的总负荷电气量分解为各个用电器的独立运行数据，并识别各个用电器工作状态以及分析用户用电行为。ILM、NILM工作原理如图1、图2所示。与ILM相比，NILM更经济、可靠，更容易普及。通过用户电能使用情况、电器信息以及用电偏好进行居民用户画像，对电网、居民用户、社会等主体在多方面有重要的实际价值与意义 [2] 。

非侵入式负荷监测按照工作流程主要分为数据的采集与处理、事件检测、特征提取、负荷识别等步骤。近年来，研究者主要从负荷特征的提取以及负荷识别算法优化两个方面开展研究。文献 [3] 以家庭用电成本、温度、时间、舒适度为目标函数建立家庭智慧用能多目标优化模型，对可控负荷、电动汽车、储能系统进行分析建立数学模型，利用粒子群算法对模型进行求解。文献 [4] 针对研究中存在的分解准确度低、算法泛化性能低等系列问题，通过应用图信号处理(Graph Signal Processing, GSP)理论，提出将基于图信号交替优化与非侵入式负荷监测相结合的方法。文献 [5] 通过实验验证了将基于V-I轨迹的负荷识别模型与基于其他负荷特征的识别算法相结合的实验方法，得出对于动态、噪声和非常相似的负荷设备，组合方案可以提供更好的整体预测精度和可靠性。文献 [6] 针对现有的非侵入式负荷监测方法难以准确识别具有相似电特性负荷的问题，通过KD树和BP神经网络提出了一种基于深度学习对识别结果进行修正的非侵入式负荷监测方法。文献 [7] 针对现有高精度的基于深度学习的负荷识别算法运算复杂度高，无法用于家庭嵌入式设备的问题，提出利用无需训练过程的k最近邻算法作为负荷识别模型对算法进性优化。文献 [8] 通过提取出电路稳态运行时的U-I特性曲线图，将其输入至双向长短时记忆神经网络中进行辨识，并利用动态时间规划算法优化辨识结果，实现高精度地负荷辨识，利用卷积神经网络提取出特征向量作为负荷印记并利用动态时间规划算法优化辨识结果，实现高精度的负荷辨识。文献 [9] 针对多目标NILM优化问题，提出使用有功功率和无功功率特征作为目标函数，根据目标函数维度，选择NSGA-II算法进行优化分类。文献 [10] 从负荷特性出发，针对各电力负荷的暂态及稳态电气特性，提取并建立负荷特征标签。然后采用极限学习机(ELM)神经网络模型，将输入特征非线性地映射到输入层，实现快速收敛至全局最优点。

Figure 1. Working principle of intrusive load monitoring

图1. 侵入式负荷监测工作原理

Figure 2. Working principle of non-intrusive load monitoring

图2. 非侵入式负荷监测工作原理

在非侵入式负荷监测研究中，根据负荷所处状态的不同，负荷特征一般分为暂态特征和稳态特征 [11] 。负荷启动或关断的动作导致负荷状态发生变化后短暂的时间内，通过监测电气量的变化，将这一暂态过程中负荷的电流脉冲峰值、暂态过程持续时间、电流凹凸系数等可量测或计算的电气量称为暂态特征，其数值称为暂态特征量。暂态特征包含了很多信息，但在实际研究中发现暂态特征并不够稳定，对于算法以及实验环境要求较高。稳态特征是指将负荷动作前后负荷处于稳定运行状态下的有功、无功、稳态电压电流等可量测或计算的电气量。因负荷电器特性的不同，稳态特征在不同负荷状态变化前后表现出的差值变化不同，在研究中便可利用各类稳态特征的变化量单独或综合进行非侵入式负荷辨识，这样的稳态特征的变化量定义为稳态特征量 [12] 。与暂态特征相比，稳态特征具有易测量、负荷辨识度高等特点，故本文选择稳态特征量作为特征开展研究。

通过对近期相关文献进行研究分析，发现目前的非侵入式负荷监测研究中的大部分研究仍将研究重点放在提升负荷识别的准确度以及效率上，针对负荷分解部分的准确率及效率方面的提升研究较少。本文针对非侵入式负荷分解部分，通过引入多目标蛇优化算法(Multiple Objective Snake Optimizer, MOSO)，针对实际使用的电器选取合适的特征开展实验，不仅提升了实验的准确率，大大节约了实验的时间，提升效率和实际应用的可行性。

2. 多目标蛇优化算法MOSO

2.1. 多目标蛇优化(MOSO)算法

蛇优化算法(Snake Optimizer, SO)是由Fatma A. Hashim和Abdelazim G. Hussien于2022年提出的一种新的元启发式算法 [13] ，该算法启发于蛇的觅食和交配行为，具备思路新颖、快速高效以及优秀的收敛性能。

蛇优化算法受蛇交配行为的启发，如果温度低且食物充足，则会发生交配，否则蛇只会寻找食物或吃掉剩余的食物。蛇优化算法分为两个阶段，即全局探索或局部开发。

2.2. 数学模型

(1) 种群初始化

种群初始化就是在搜索空间内随机产生N个体作为原始种群进行计算，将每个个体的每一维随机产生一个取值范围以内的数。即：

$X_i=X_{\min }+r\cdot \left(X_{\max }-X_{\min }\right)$ (1)

其中，r是 $\left[0,1\right]$ 之间的随机数，X_i是种群中的个体，而X_min和X_max分别为取值范围的上下边界。

(2) 将种群分为雌、雄两个子种群

假设雄性个体的数量，默认剩余个体为雌性个体。这样，种群就被分为两组：雄性组和雌性组。

$N_f=N-N_m$ (2)

其中，N为种群中的个体数，即种群规模；N_f为雌性个体数；N_m为雄性个体数。

(3) 全局搜索

如果食物数量Q < 阈值，蛇通过选择任何随机位置来搜索食物，并更新它们的位置。

雄性蛇位置更新：

$X_{i,m}\left(t+1\right)=X_{rand,m}\left(t\right)\pm c_2\times A_m\times \left(\left(X_{\max }-X_{\min }\right)\times rand+X_{\min }\right)$ (3)

其中， $X_i{}_{,m}$ 为第i只雄性蛇的位置， $X_{rand}{}_{,m}$ 为随机选择的雄性蛇的位置，rand是0到1之间的随机数，c₂为常数，取值为0.05。A_m为雄性蛇找到食物的能力，计算方法如下：

$A_m=\exp \left(\frac{-f_{rand,m}}{f_{i,m}}\right)$ (4)

其中， $f_{rand}{}_{,m}$ 为 $X_{rand}{}_{,m}$ 的适应度，而 $f_i{}_{,m}$ 为 $X_i{}_{,m}$ 的适应度。

雌性蛇位置更新：

$X_{i,f}\left(t+1\right)=X_{rand,f}\left(t+\text{1}\right)\pm c_2\times A_f\times \left(\left(X_{\max }-X_{\min }\right)\times rand+X_{\min }\right)$ (5)

其中， $X_i{}_{,f}$ 为第f只雌性蛇的位置， $X_{rand}{}_{,f}$ 为随机选择的雌性蛇的位置。A_m为雌性蛇找到食物的能力，计算方法如下：

$A_f=\exp \left(\frac{-f_{rand,f}}{f_{i,f}}\right)$ (6)

其中， $f_{rand}{}_{,f}$ 为 $X_{rand}{}_{,f}$ 的适应度，而 $f_i{}_{,f}$ 为 $X_i{}_{,f}$ 的适应度。

(4) 局部搜索

如果Q > 0.25，且温度>0.6，则蛇只会向食物移动：

$X_{i,j}\left(t+1\right)=X_{food}\pm c_3\times Temp\times rand\times \left(X_{food}-X_{i,j}\left(t\right)\right)$ (7)

其中， $X_i{}_{,f}$ 为个体(雄性或雌性)蛇的位置，X_food为最佳个体的位置，c₃为常数，等于2，Temp为温度。

如果Q > 0.25，且温度<0.6，则蛇将处于战斗模式或交配模式。

a) 战斗模式

雄性蛇位置更新：

$X_{i,m}\left(t+1\right)=X_{i,m}\left(t\right)+c_3\times FM\times rand\times \left(Q\times X_{best,f}-X_{i,m}\left(t\right)\right)$ (8)

$FM=\exp \left(\frac{-f_{best,f}}{f_i}\right)$ (9)

其中， $X_{best}{}_{,f}$ 为雌蛇组中的最佳位置，rand是 $\left[0,1\right]$ 范围内的随机数，FM为雄性蛇的战斗能力。

雌性蛇位置更新：

$X_{i,f}\left(t+1\right)=X_{i,f}\left(t\right)+c_3\times FF\times rand\times \left(Q\times X_{best,m}-X_{i,F}\left(t\right)\right)$ (10)

$FF=\exp \left(\frac{-f_{best,m}}{f_i}\right)$ (11)

其中， $X_{best}{}_{,m}$ 为雄蛇组中的最佳位置，rand是 $\left[0,1\right]$ 范围内的随机数，FF为雌性蛇的战斗能力。

b) 交配模式

雄性蛇位置更新：

$X_{i,m}\left(t+1\right)=X_{i,m}\left(t\right)+c_3\times M_m\times rand\times \left(Q\times X_{i,f}\left(t\right)-X_{i,m}\left(t\right)\right)$ (12)

$M_m=\exp \left(\frac{-f_{i,f}}{f_{i,m}}\right)$ (13)

其中，M_m表示雄性蛇的交配能力。

雌性蛇位置更新：

$X_{i,f}\left(t+1\right)=X_{i,f}\left(t\right)+c_3\times M_f\times rand\times \left(Q\times X_{i,m}\left(t\right)-X_{i,f}\left(t\right)\right)$ (14)

$M_f=\exp \left(\frac{-f_{i,m}}{f_{i,f}}\right)$ (15)

其中，M_m表示雌性蛇的交配能力。

2.3. 算法流程

MOSO算法流程如下：

(1) 采集居民用户用电数据。

(2) 获得数据中的负荷有功功率和电流有效值，并对其进行归一化处理，方便简化计算。

(3) 定义多目标蛇优化算法的参数。

(4) 根据公式(1)、(2)产生初始雄性、雌性种群。

(5) 根据公式(3)、(4)、(5)、(6)计算出阈值，并更新雄性、雌性种群的位置，根据最优开断信息计算分离负荷信息。

(6) 判断食物数量与温度是否达到目标，若没有则进入战斗模式或交配模式。

(7) 输出最优解。

算法流程图如图3所示。

Figure 3. MOSO flow chart

图3. MOSO算法流程图

3. 实验分析

3.1. 实验环境和实验数据

本文实验数据来源于安装Lab VIEW和信号采集卡的数据采集终端，采集系统运行过程中的电流、电压等数据。获取实测数据后，为了验证本文算法的有效性和先进性，用MATLAB编程实现数学建模，利用本文算法进行对数据进行负荷分解及辨识。

由于本文的研究工作最终将面向需求响应，实现用户侧负荷辨识与控制功能。本文选取三种常用居民负荷特征热水壶、白炽灯、电视机进行实验并采集数据。

3.2. 实验参数设置

参数采样率f_s = 10 kHz，负荷种类m = 3，分别是热水壶、白炽灯、电视机。样本种群大小N = 30，最大迭代次数maxgen = 20，每个维度中的网格数ngrid = 10。

3.3. 实验结果

使用MATLAB软件对本文所提出的多目标蛇优化算法模型进行测试，实验结果如图4所示。

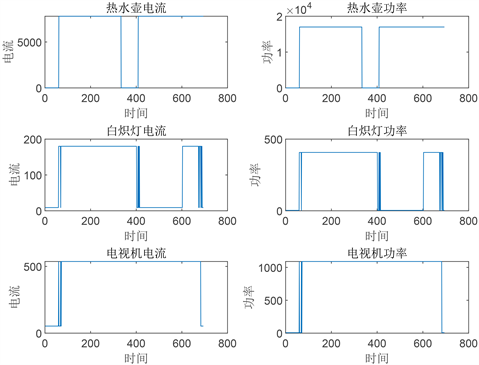
Figure 4. Three common stress measurement results

图4. 常见三种负荷实验结果

根据实验结果，整理得到表1。

Table 1. Electrical steady-state worksheet

表1. 电器稳态工作表

从表1中可反映出，不同负荷的有功功率值差别较明显，因此基于负荷的有功功率进行负荷辨识具有一定的对比性，但当部分设备的有功功率值较接近时，易造成辨识结果错误。所以本文引入稳态电流辅助完成负荷辨识。

为了验证本文算法的先进性，采用遗传算法(Genetic Algorithm, GA)对同一数据开展分类预测，两类算法的实验结果如图5、图6所示。

Figure 5. MOSO algorithm experimental results

图5. MOSO算法实验结果

Figure 6. GA algorithm experimental results

图6. GA算法实验结果

为了评估两种算法的有效性和准确性，本文采用平均绝对误差(Mean Absolute Error, MAE) [14] 对算法结果进行评估。其具体计算方法如下所示：

$E_{MAE\left(p\right)}=\frac{1}{n}{\displaystyle \underset{n}{\sum }\left|{\hat{p}}_j\left(n\right)-p_j\left(n\right)\right|}$ (16)

$E_{MAE\left(i\right)}=\frac{1}{n}{\displaystyle \underset{n}{\sum }\left|{\hat{i}}_j\left(n\right)-i_j\left(n\right)\right|}$ (17)

式中：E_MAE(p)为MAE功率相对分解误差；E_MAE(i)为MAE电流相对分解误差；n为采样点计数；p_j(n)为第j个用电设备在第n个采样点的功率分解值；p_j(n)为第j个用电设备在第n个采样点的功率真实值；i_j(n)为第j个用电设备在第n个采样点的电流分解值；i_j(n)为第j个用电设备在第n个采样点的电流真实值。同时，为验证本文算法在实际工作中效率上的优越性，对实验所需时间进行测量对比，两种算法的平均绝对误差及实验时间如表2所示。

Table 2. Comparison of experimental results of MOSO algorithm and GA algorithm

表2. MOSO算法与GA算法实验结果对比

由表2可以看出，相较于传统GA算法，MOSO算法在对电流及功率的识别上具有更高的准确率。同时，MOSO算法可以实现同时对数据进行分解及对比，MOSO算法的运行所需时间远低于GA算法，在非侵入式负荷分解上具有更高的效率。

4. 结论

本文通过对目前NILM领域中的研究进度和方向进行总结分析，针对负荷分解这部分开展研究。通过对家中最常见的家用电器进行分析，选取了稳态电流及功率作为特征开展负荷和分解，通过引入MOSO算法，对负荷数据同时进行分解及对比，在提升识别数据准确率的同时大大节省时间。

NOTES

^*第一作者。

^#通讯作者。