1. 引言
超临界二氧化碳布雷顿循环因具有效率高、布置形式简单、结构紧凑等优势而受到了广泛关注 [1] [2] [3] [4] 。透平作为超临界二氧化碳布雷顿循环中最重要的做功部件,其性能的优劣直接决定着整个系统的效率 [5] [6] [7] 。与轴流式透平相比,向心透平具有组成部件少、结构简单紧凑、单级焓降大等优点 [8] [9] [10] [11] 。国内外学者对向心透平在S-CO2循环发电系统中的应用进行了深入研究。
王巧珍 [12] 基于粒子群优化算法,开展超临界二氧化眼向心透平优化设计,并采用CFD数值模拟方法对超临界二氧化碳向心透平的变工况性能进行了分析,结果表明,设计的透平在一定范围内具有良好的变工况性能。清华大学的周奥铮等人 [13] 设计了一台1.5 MW级超临界二氧化碳向心透平并进行了CFD数值模拟和变工况性能预测,透平总体参数满足设计要求。Muhammad Saeed等人 [14] 开发了一款透平优化设计程序,基于该程序设计了应用于聚光太阳能电站的10 MW级超临界二氧化碳向心透平。Antti Uusitalo等人 [15] 对超临界二氧化碳离心透平进行研究,并将设计结果与相应的向心透平进行了比较,结果表明,所研究的两种涡轮均能达到较高的等熵效率,范围在85%~90%之间。
目前,针对超临界二氧化碳透平的研究多采用CFD数值模拟的方法,由于轴流式透平设计时动静叶片数往往成比例,因此在对轴流透平进行数值模拟时,大多采用单流道域进行计算,从而可以节约计算资源和加快计算速度。但向心透平在设计时节距比一般不为整数,因此在对其进行数值模拟时,采用单流道作为计算域是否可靠的方法仍有待商榷,超临界二氧化碳的特殊物性也给CFD数值模拟带来了一定困难。
本文基于自主设计的10 MW级超临界二氧化碳向心透平,分别选取单流道和全周流道作为计算域,采用不同的真实气体性质计算方法:雷德利希–邝氏状态方程(R-K方程)、彭–罗宾森方程(P-R方程)和真实气体性质(RGP)表,对超临界二氧化碳向心透平的数值模拟方法展开研究。
2. 向心透平模型
选取自主设计的10 MW级超临界二氧化碳向心透平为研究对象,透平的主要性能参数如表1所示。

Table 1. Performance parameters of S-CO2 centripetal turbine
表1. S-CO2向心透平性能参数
透平的导叶栅采用了气动性能良好的TC-4P叶型,具体的几何参数和型线如表2所示。动叶轮的子午流线采用由5个点控制的贝塞尔曲线生成,具体几何参数及其子午面形状如表3所示。

Table 2. Guide vane cascade profile and geometric parameters
表2. 导叶栅型线及几何参数

Table 3. Meridian surface and geometric parameters of impeller
表3. 叶轮子午面及几何参数
超临界二氧化碳向心透平的三维造型如图1所示。其中,导叶叶片数为22,动叶轮叶片数为13。为了防止叶轮碰撞导叶,静叶和动叶之间需存在一定间隙,动静间隙不仅能使流入叶轮的气流变得均匀,还能减少噪音、减小导叶冲蚀,本文中透平的动静间隙为0.0142 m。
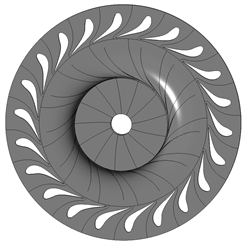
Figure 1. Centripetal turbine 3D modeling
图1. 向心透平三维造型
3. 数值模拟
3.1. 控制方程及湍流模型选取
叶轮机械的内部流动较为复杂,常采用N-S方程进行求解。目前,N-S方程的求解方法主要包括雷诺时均法(RANS)、大涡模拟法(LES)和直接模拟法(DNS)。其中,雷诺时均法(RANS)不仅能够满足工程求解精度的要求,还具有耗时短,节约计算资源的优点。因此,本文采用雷诺时均法(RANS)对N-S方程进行求解。具体控制方程如下:
连续性方程:
(1)
能量方程:
(2)
动量方程:
(3)
由于叶轮内部的流动情况十分复杂,不满足层流流动的条件,对湍流流动的流体进行数值模拟时,需要添加合适的湍流模型来使求解的方程封闭。研究表明,对于叶轮机械内部的复杂流动,基于k-ω模型基础上改进得到的SST湍流模型在计算精度上较高,缺点是不容易收敛,对网格质量要求较高。本文选择SST湍流模型进行求解。
3.2. 计算域选取
目前,大多数关于超临界二氧化碳向心透平的数值模拟为了节约计算资源和保证计算速度,常采用单流道作为计算域,但由于向心透平静叶片数与动叶片数一般不成比例,因此,采用单流道作为计算域的可靠性有待研究。本文采用单流道和全周流道分别进行CFD数值模拟,单流道和全周流道计算域如图2所示:

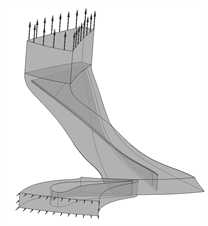 (a) 单流道计算域 (b) 全周流道计算域
(a) 单流道计算域 (b) 全周流道计算域
Figure 2. Single channel and full cycle channel calculation domain
图2. 单流道和全周流道计算域
3.3. 网格划分
将所建立好的动叶和静叶分别导入到Ansys Turbogrid中进行网格划分,划分方法选择自动拓扑划分网格(ATM),在划分网格时,y+的取值需满足湍流模型的要求,介于30~50之间。为了保证计算的准确性和高效性,需要进行网格无关性验证,如图3所示,在网格量较小时,透平效率随网格数变化较大,随着网格数的不断增大,透平总–静效率随之增大,在网格数约为126万时,继续增大网格数,透平总–静效率基本保持不变,约为92.7%。因此为了节约计算资源和保证计算速度,最终确定导叶栅单流道网格数为757,300,全周流道网格数为16,660,600;动叶轮单流道网格数为1,266,640,全周流道网格数为16,466,320,单流道计算域和全周流道计算域网格分别如图4和图5所示。
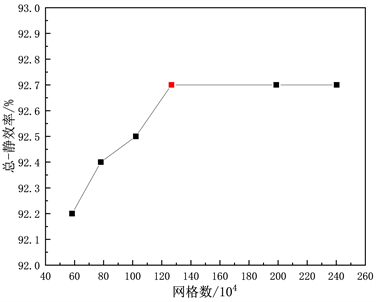
Figure 3. Grid independence verification
图3. 网格无关性验证

Figure 4. Single channel computational domain grid
图4. 单流道计算域网格
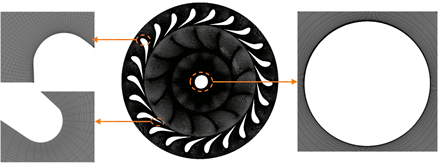
Figure 5. Full cycle flow channel computational domain grid
图5. 全周流道计算域网格
3.4. 边界条件设置
利用CFX进行三维计算,在CFX-Pre中进行边界条件的相关设置,参考压力为0 MPa,传热模型为Total Energy,进出口边界条件为总压进口静压出口,收敛标准设置为RMS10e-5,最大迭代步数为2000步。CFX中有关动静交界面主要包括两种方法,分别为冻结转子法(Frozen Rotor)和混合平面法(Mixing Stage)。冻结转子法的转子和静子之间相对位置不变,坐标系改变,适用于流体速度远大于交界面的机械转速,具有计算量小的优点,但需要上下游节距比尽量为1,以减小计算误差。混合平面法则考虑时均作用,在交界面上采用的是周向平均的方法,计算量较大,但在计算时不需要节距比接近1且计算精度高于冻结转子法。本文的动静交界面采用混合平面法进行计算。有关材料方面,目前关于超临界二氧化碳工质的选择常采用CFX内部MATERIALS-redkw数据库下的“CO2 RK”工质或MATERIALS-pengrob数据库中的“CO2”工质,CFX中采用四阶多项式进行模拟,以此保证较高的计算精度。其中,R-K方程的一般形式为:
(4)
式中:P为工质压力;R为气体常数;T为工质的温度;Vm为摩尔体积,a和b为修正系数,分别用来修正分子间引力和体积。
P-R方程的一般形式为:
(5)
式中:R为气体常数;T为工质的温度;v为工质比热容;a、b为方程参数,具体如下式所示:
(6)
(7)
(8)
式中:Tc和Pc为临界温度和临界压力,F为偏心因子ω的函数:
(9)
先选取MATERIALS-redkw数据库下的“CO2 RK”工质进行数值模拟,后续将对材料部分进行详细介绍。
4. 结果和分析
单流道计算域和全周流道计算域数值模拟结果如表4所示。单流道和全周流道模拟结果中质量流量、透平功率及轴效率与设计值的相对误差均在3%以内,且单流道和全周流道模拟结果中质量流量、透平功率及轴效率的误差分别为0.13%、1.3%、1.3%,误差较小。由此可以验证,在对向心透平进行数值模拟时采用单流道作为计算域的可靠性和准确性。

Table 4. Single channel and full cycle channel calculation results
表4. 单流道和全周流道计算结果
由于超临界二氧化碳的物性与常规流体不同,其密度接近液体,粘度近似于气体,因此,采用真实气体方程计算超临界二氧化碳物性是否准确仍有待商榷,本文采用3种不同的真实气体计算方法对透平进行模拟,分别为:真实气体R-K方程、真实气体P-R方程以及外部生成真实气体性质(RGP)表供CFX调用的方法,来研究不同计算方法对超临界二氧化碳物性的评估准确性。由于前面已经证明了单流道计算域的可行性,因此在后续分析计算过程当中将采用单流道作为计算域,这样可以大大加快计算速度和节约计算资源。其中,RGP表的规格如表5所示。
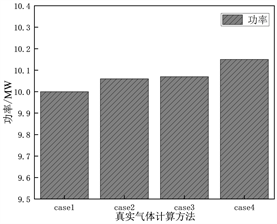
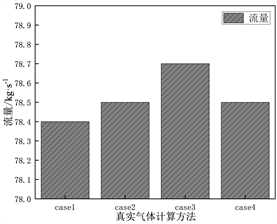
将设计值命名为case1,三种不同真实气体计算方法:RGP表、R-K方程、P-R方程分别为case2,case3,case4,不同真实气体计算方法对透平流量、功率及效率的影响如图6所示。采用真实气体性质表(case2)所计算出的透平流量、功率及效率分别为78.5 kg∙s−1、10.06 MW、84.9%,与设计值(case1)相对误差较小,分别为−0.13%、−0.6%、0%;真实气体R-K方程(case3)所计算出的透平流量、功率及效率分别为78.7 kg∙s−1、10.07 MW、84.3%,与设计值误差分别为−0.38%、−0.7%、0.71%;真实气体R-K方程(case3)所计算出的透平流量、功率及效率分别为78.5 kg∙s−1、10.15 MW、85.2%,与设计值误差分别为−0.13%、−1.5%、−0.35%。三种不同真实气体性质计算方法在对超临界二氧化碳透平的流量、功率及效率计算方面具有一定的准确性和可靠性,与设计值的相对误差均在3%以内,采用真实气体性质表(RGP)所计算的结果最为准确。
 (a) 流量 (b) 功率
(a) 流量 (b) 功率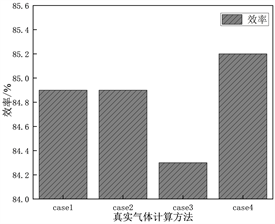 (c) 效率
(c) 效率
Figure 6. Influence of different real gas calculation methods on turbine flow, power and efficiency
图6. 不同真实气体计算方法对透平流量、功率及效率的影响
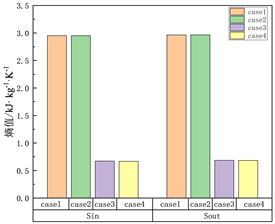
三种不同真实气体性质计算方法对超临界二氧化碳的物性计算如图7所示,其中,Hin和Hout分别表示透平入口和出口的焓值,Sin和Sout分别表示透平入口和出口的熵值。从图中可以看到,采用真实气体性质方程所计算出的超临界二氧化碳焓值和熵值与实际气体存在较大差异,R-K方程(case3)、P-R方程(case4)计算结果中透平入口焓值与设计值(case1)误差分别为34.54%和34.50%,透平出口焓值与设计值误差分别为38.92%和38.95%,透平入口熵值与设计值误差分别为77.23%和77.36%,透平出口熵值与设计值误差分别为76.83%和76.52%,而采用真实气体性质表(case2)的模拟结果中,透平焓值和熵值与真实气体的焓值和熵值表现出较高的一致性。从图中还可以观察到,虽然两种不同真实气体性质方程在焓值和熵值的计算方面与实际气体存在较大误差,但透平内部焓降(Hin-Hout)与设计值基本一致,因此采用真实气体性质方程在对透平性能参数的评估方面具有一定的准确性。
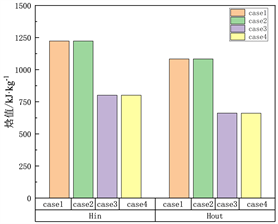 (a) 焓值 (b) 熵值
(a) 焓值 (b) 熵值
Figure 7. Physical properties of S-CO2 calculated by different real gas calculation methods
图7. 不同真实气体计算方法对S-CO2物性计算结果
5. 结论
本文针对超临界二氧化碳向心透平的CFD数值模拟方法进行研究,主要结论如下:
(1) 在对超临界二氧化碳向心透平进行数值模拟时,单流道域和全周流道域计算结果中质量流量、透平功率及轴效率与设计值的误差均在3%以内,采用单流道作为计算域,可以大大节约计算资源和加快计算速度。
(2) 三种不同真实气体性质计算方法:R-K方程、P-R方程、RGP表在超临界二氧化碳向心透平的性能评估方面具有一定准确性,计算结果中透平主要性能参数与设计值误差均在3%以内。
(3) R-K方程、P-R方程在对超临界二氧化碳的焓值与熵值计算方面存在较大误差,采用外部生成RGP表供CFX调用的方法更为准确。