1. 问题提出
本文问题提出基于2023年第十五届“华中杯”大学生数学建模挑战赛 [1] 中的A题,即为探究某药物研究中心的新型镇静药物临床实验疗效,附件中提供了1245名患者的185项指标数据,其中包括患者的基线特征、进药后的生命体征、术中术后的不良反应等数据。基于上述背景,分别解决以下三个问题。
问题1:分析附件中关于术中、术后24 h不良反应,新药组和原有药物组是否存在显著差异;并根据患者基本信息和镇静药物种类,对患者术中、术后24 h的不良反应进行预判。
问题2:分析新药组和原有药物组在生命体征数据方面是否表现出显著差异;若有显著性差异,分析出造成显著性差异的因素。
问题3:根据患者的基本信息及用药信息,建立数学模型对其用药后三分钟内的IPI数据进行预测。
2. 模型假设
本文拟建立多种预测分析模型来解决以上三个问题。在建立模型之前,先提出模型成立的假设条件:假设患者所填写的问卷信息效度和信度分析均良好。
假设患者生命体征记录数据误差在合理范围内,不影响后续回归分析与预测。假设不平衡的问卷数据不会影响模型效果。假设空缺的数据不会对模型造成太大影响。
3. 符号说明
在本文中,使用了一些特定的符号来表示不同的概念和信息,具体符号意义如表1所示。

Table 1. Explanation of mathematical symbols
表1. 数学符号说明
4. 模型的求解与结果分析
4.1. 问题1模型建立与求解
4.1.1. 数据预处理
(一) 术中情况分析
Step 1术中不良反应特征值划分。
经观察,发现有48名患者在术中有除呛咳、体动以外的不良反应,且这些反应分为“打嗝”、“打呼”、“打嗝 + 打呼”三种,我们将具有“打嗝 + 打呼”不良反应的数据拆分为“打嗝”和“打呼”两条数据,因此,术中其他不良反应有“无”、“打嗝”、“打呼”三个特征值。
Step 2呕吐次数异常值处理。
对于术后24 h出现呕吐反应但并未填写呕吐次数的患者,我们采用众数(1次)填补缺失值的方法对他们的呕吐次数进行赋值;对于填写451号患者填写的“四五次”,我们将其呕吐次数赋值为4次;对于986号患者填写的“多次”,我们将其呕吐次数赋值为5次。
4.1.2. Pearson卡方检验模型
卡方检验通过比较两项或多项频数,检测在一定显著性水平上实际频数与以某种理论模型或分布特征假设为基础的期望频数的差异度。对于术中、术后24 h不良反应与镇静药物种类之间的相关性:
(1)
Step 1:建立原假设
:使用不同镇静药物对术中、术后24 h的不良反应没有影响,即镇静药物种类与不良反引发中无显著性差异。Step 2:根据理论分布计算期望频数。Step 3:根据实际频数和期望频数计算样本卡方值。Step 4根据自由度和显著性水平
在卡方分布表中查找出对应卡方临界值。设置显著水平
,计算
。若
,则接受原假设,反之,接受备择假设。
经过上述操作,取
,对术中不良反应的卡方检验结果如表2所示。

Table 2. Chi-square test results of intraoperative adverse reactions in the new drug group and the existing drug group
表2. 新药组和原有药物组对术中不良反应的卡方检验结果
从上表可以看出:对于“体动”这一不良反应,其P值为0.036 (
),水平上呈现显著性,拒绝原假设,即新药组和原有药物组存在显著性差异。而对于“呛咳”和“术中其他”这两种不良反应,其
均大于0.05,接受原假设,即新药组和原有药物组不存在显著性差异。
(二) 术后24 h情况分析
表3为关于新药组和原有药物组对术后24 h不良反应的卡方检验结果。

Table 3. Chi-square test for postoperative adverse reactions between the new drug group and the existing drug group at 24 hours
表3. 新药组和原有药物组对术后24 h不良反应的卡方检验
对于“恶心”、“头昏”、“乏力”、“腹胀”、“腹痛”这5个不良反应,其
均小于0.05,水平上呈现显著性,拒绝原假设,即新药组和原有药物组存在显著性差异。而对于其余的不良反应,其
均大于0.05,接受原假设,即新药组和原有药物组不存在显著性差异。
4.1.3. T检验模型
独立样本T检验用于检验两分组数据是否存在显著性差异,由于出现呕吐次数为定量指标,所以我们采用独立样本T检验模型对其进行检验。建立原假设
:镇静药物种类对呕吐次数没有影响,即镇静药物种类在呕吐次数上无显著性差异。
检验结果:新药组和原有药物组在出现呕吐次数上的均值分别为:0.066、0.152;显著性结果P值为0.109 (
),因此统计结果不显著,接受原假设,说明新药组和原有药物组在出现呕吐次数上不存在显著差异。
第一小问结论:对于术中不良反应“体动”、术后24 h不良反应“恶心”、“头昏”、“乏力”、“腹胀”、“腹痛”,新药组和原有药组存在显著性差异。
4.1.4. 不良反应预判
Step 1:数据预处理。
对于198号患者,其年龄值为空,故剔除该患者的临床实验数据。
Step 2:特征编码。
根据第一小问的结论,筛选出术中、术后24小时有以上不良反应的患者的基本信息及其使用镇静药物的种类,为便于后续回归模型的建立,对非数值型特征值进行编码。
Step 3:建立回归模型。
逻辑回归Logistic回归模型是对线性回归模型的结果做出的sigmoid映射,映射函数为:
(2)
该函数可将所有函数值映射到(0, 1)区间内,即将逻辑回归的结果转化为(0, 1)之间的概率值,由此构造分段函数,即可实现二分类问题。
随机森林 [2] 随机森林是将随机子空间与Bagging集成学习两种方法相结合的结成算法。随机森林由一系列相互之间不相关的的决策树组成森林,结果为多棵决策树投票表决的结果,故其分类结果比单棵决策树分类结果要理想很多。
XGBoost模型 XGBoost全称是Extreme Gradient Boosting,又被称为极限梯度提升算法。XGBoost模型集优秀的模型效果和迅速的运算速度于一体,在ui规模性上拥有超高的运算性能。XGBoost模型是在传统梯度提升模型的基础上进行改进优化,通过多次迭代累,将多个弱评估器组合成一个强评估器,以获得更好的回归表现。其本身亦属于集成学习算法。
Step 4:模型集成。
集成模型采用投票法的方式实现,使用Scikit-learn库中的VotingClassifier类,将逻辑回归模型、随机森林模型和XGBoost模型传入,我们将投票方式设置为“硬投票”,即直接取各模型的预测结果中得票最多的类别作为集成模型的预测结果。接着,我们使用fit方法在训练集上训练投票模型,并使用predict方法在测试集上进行预测。最后,我们计算集成模型预测准确率。
通过表4,可以看出逻辑回归模型、随机森林模型、XGBoost模型在未经集成处理的情况下表现效果就已经很优秀了,各模型预测准确率均高于89%。通过模型的集成,使得最终模型的预测准确率均高于91%。
4.2. 问题2模型建立与求解
4.2.1. 数据预处理
附件中提供了收缩压(mmHg)、舒张压(mmHg)、PetCO2 (mmHg)、呼吸(次/分)、SpO2 (%)、心率(次/分)及IPI、MOAA/S评分这八个生命体征指标,并记录了患者在诱导前后的一些时间段及手术后这些指标的具体数据值。经过观察,我们发现收缩压诱导后20 min (sbp20)、MOAA/S评分诱导后20 min (moaas20)、舒张压诱导后2.5 min (dbp025)的数据值缺失率均超过85%,故我们将这些特征指标进行了删除。对于生命体征数据其他的缺失值,我们采用了均值填补的方式对其进行了处理。
4.2.2. 独立样本Mann-Whitney检验
独立样本Mann-Whitney检验(Mann-Whitney U检验),也称为Wilcoxon秩和检验,是一种用于比较两个独立样本的非参数假设检验方法。这个检验方法的原理是将两组样本合并,按照观测值的大小顺序排列,然后计算每个样本中的秩次。然后,通过比较两个样本的秩次总和来确定它们是否来自于相同的总体分布。
Step 1:建立原假设
:在原有药组和新药组中第P个生命体征的特征集没有显著不同。Step 2:设置拒绝零假设的阈值
。Step 3:对生命体征数据按照新药组
和原有药物组
进行独立样本Mann-Whitney检验。Mann-Whitney检验统计量
、
的计算公式如下:
(3)
(4)
式中:
、
的最小值用于与显著检验阈值
相比较,若
,则拒绝假设
,即两特征之间存在差异。
经过上述步骤,我们筛选出57条拒绝零假设的生命体征项,即原有药组和新药组在这57个生命特征项下呈显著性差异。下表5为部分筛选结果。

Table 5. Partial vital sign items and their test results that reject the null hypothesis
表5. 拒绝零假设的部分生命体征项及其检验结果
4.2.3. 造成在生命体征数据方面呈现显著性差异的因素
Lasso回归是一种线性回归方法,它通过加入一个L1正则化项来对模型进行约束和选择。
Step 1:分别以患者基本信息和镇静药物种类为自变量,具有显著性差异的生命体征项作为因变量建立Lasso回归模型。加入L1正则化后的Lasso损失函数式(5)所示
(5)
式中,n为样本个数,
为惩罚值,
为L1正则化。
Step 2:我们以训练集:测试集 = 8:2的比例对数据集进行划分。
Step 3:确定Lambda值,并基于最佳的lambda值建立Lasso回归模型(下以诱导前1~3 min的PetCO2 为例)通过交叉验证,得到不同λ取值下Lasso模型的可视化效果,见图1。
对于图1,其横坐标代表λ的对数取值,纵坐标代表拟合模型的均方误差。
图2为Lasso拟合系数轨迹,其给出了在不同λ取值下各特征拟合系数值的变化情况及影响因素的筛选结果。
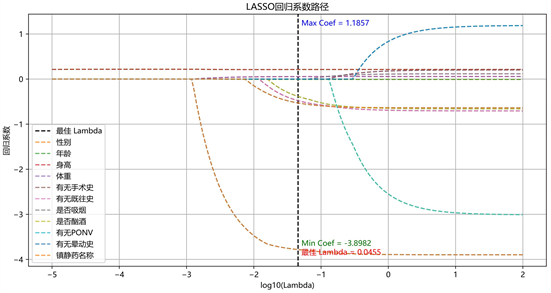
Figure 2. The relationship between different λ value and characteristic variable coefficient value
图2. 不同λ取值与特征变量系数值之间的关系
为得到更精确的模型,我们选用误差最小时的 取值,即
,此时的模型中包含特征变量数10个,将它们分别表示为
并将其具体系数表示为
,其中截距项
。见表6。

Table 6. Characteristic variable coefficient value with minimum model error
表6. 模型误差最小时特征变量系数值
Step 4:确定影响比重最大的因素。
Lasso回归中的标准化系数(也称为L1范数)表示每个特征的重要性或权重大小。在Lasso回归中,标准化系数越高的特征表示其在模型中的贡献越大,因此可以认为它们与目标变量之间的关系更为密切,与之相关性更高。
我们找出每个模型标准化系数最大值对应的特征作为体征造成在生命体征数据方面呈现显著性差异的因素。仍以诱导前1~3 min的PetCO2为例,由表5可以得到各特征变量的系数之间的关系如式(6)所示:
(6)
即对于诱导前1~3 min的PetCO2,选取“性别”作为造成在生命体征数据方面呈现显著性差异的因素。同上理,我们对第一小问中筛选出的57个生命体征项逐一进行Lasso回归分析,得到部分结果如下表7所示:
由此可见,造成在生命体征数据方面呈现显著性差异的因素不一定是新型镇静药物的使用,还有可能是性别、年龄、有无晕动史等。
4.3. 问题3模型建立与求解
4.3.1. 数据预处理
IPI指标是刻画生命体征的核心指标。由前文的IPI指标分类可知,IPI指标在区间(1, 10)内,不同指标对应着患者不同的临床状态。根据题目要求,我们将患者诱导后0.5 min的IPI (IPI005)、诱导后1 min的IPI (IPI1)、诱导后1.5 min的IPI (IPI015)、诱导后2 min的IPI (IPI2)、诱导后2.5 min的IPI (IPI025)、诱导后3 min的IPI (IPI3)这6项生命体征指标提取出来。对于缺失值,我们采取众数填补;对于591号患者,其IPI值填写为0,数据异常,故在本题将该患者的数据剔除。
4.3.2. 建立预测模型
本题欲采用下述三种数学模型对6项IPI指标进行预测:
SVM模型SVM指支持向量机(Support Vector Machine),其主要思想是将数据映射到高维空间中,使得在该空间中能够找到一个最优的超平面,将数据分成两个类别。在找到最优超平面的过程中,SVM依赖于一些被称为“支持向量”的数据点,这些点距离最优超平面最近。
决策树模型的基本思想是将数据分成多个小组,每个小组具有相同的属性,并且每个小组都属于一个类别。这种分组可以通过一系列的决策来完成,每个决策都是基于数据的某个属性。决策树从根节点开始,通过一系列分支和叶子节点来表示不同的决策路径。
在决策树算法中,每个分支代表一个属性,每个叶子节点代表一个类别。通过分裂数据,决策树算法找到了最重要的属性,这些属性能够帮助我们对数据进行分类。
BP神经网络模型 [3] BP神经网络(Back Propagation Neural Network)是一种常用的人工神经网络模型,由输入层、隐藏层和输出层组成。每个层都由一些神经元组成,神经元之间通过加权连接相互作用。BP神经网络使用反向传播算法来训练模型,该算法可以根据误差信号将误差反向传播到每个神经元中,然后使用梯度下降算法来更新每个神经元的权重和偏置。
BP神经网络的训练过程包括两个阶段:前向传播和反向传播。前向传播将输入数据传递到输出层,计算输出层的误差,然后将误差反向传播回隐藏层,通过调整每个神经元的权重和偏置来更新模型。这个过程不断迭代,直到模型收敛为止。
Step 1:以用药信息和患者信息为自变量,3分钟以内的IPI数据作为因变量,分别建立SVM、决策树、BP神经网络三种模型。
Step 2:按照训练集:测试集 = 8:2来训练模型。
Step 3:通过比较各个模型的评估参数,找出对于各个阶段IPI数据的最优预测模型。
4.3.3. 最优模型的选择
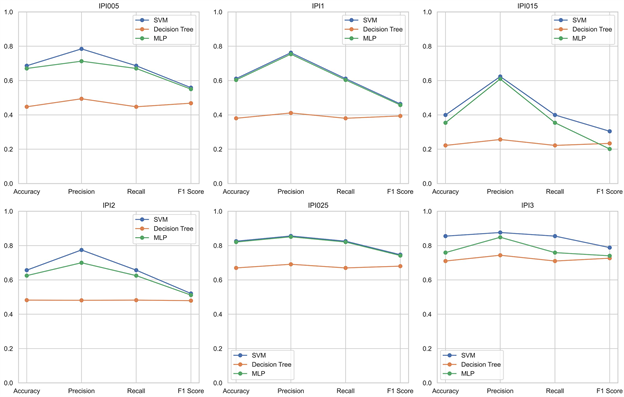
Figure 3. Evaluation indicators based on three prediction models
图3. 基于三种预测模型的评价指标
其中Accuracy、Precision、Recall、F1均为评价模型的重要指标。Accuracy:预测正确样本占总样本的比例,准确率越大越好。Precision:预测出来为正样本的结果中,实际为正样本的比例,精确率越大越好。Recall:实际为正样本的结果中,预测为正样本的比例,召回率越大越好。F1:精确率和召回率的调和平均,精确率和召回率是互相影响的,虽然两者都高是一种期望的理想情况,然而实际中常常是精确率高、召回率就低,或者召回率低、但精确率高。若需要兼顾两者,那么就可以用F1指标。
我们对所有模型均进行了以上四项评价指标的评估,得到评估结果如图3所示。基于图3得到最优预测模型如表8所示。

Table 8. Determination of the optimal prediction model
表8. 最优预测模型的确定
对于指标IPI025,BP神经网络模型较SVM模型、决策树模型预测效果更好;对于指标IPI005、指标IPI1、指标IPI015、指标IPI2和指标IPI3,SVM模型的预测效果最好。
5. 模型的评价及推广
5.1. 模型评价
构建预测不良反应模型中通过集成模型的方法对不良反应进行预测,融合多个模型的优点,有效提高模型预测精度。使用数据的秩进行分析减少了异常值和离群值的影响并筛选出表现出显著差异的生命体征指标,使回归分析的结果更加准确。在预测IPI数据中,使用多模型和评价指标选出最优模型,让预测更加精准。
构建集成模型中,数据量需要足够大,否则结果会失真,此时通过合并一些类别,以增加每个类别的样本数量,从而更接近样本数量足够大的情况。当问题中存在大量相同值时,再进行预测会导致信息丢失,会影响筛选生命指标,这种情况可以将相同的数值合并为一个秩次,然后计算平均秩次。这样可以避免丢失太多信息。
5.2. 模型推广
对于此次两种镇静药物的临床实验疗效分析与预测有重要的现实意义。本文所提出的模型可以为临床医生在使用镇静药物时更好地预防和减轻不良反应的发生提供参考和建议,使得临床医生更好地把握各种生命体征的变化情况,及时调整镇静药物的用药剂量和种类,以达到更好的临床治疗效果。
此外,本研究的方法和模型也可以为相关学科领域提供一种有效的研究思路和方法,例如药学、统计学和数据挖掘等领域,可以参考我们所使用的数据预处理方法和建立的模型框架,以及模型评价指标等方面的经验。
最后,我们希望本文的研究成果可以为相关疾病的临床治疗和药物研发提供有益的参考和启示,为人类健康事业做出一份微薄的贡献。
NOTES
*通讯作者。